三自由度架管机机械臂动力学特性分析

陈 星，邓海顺，鲍 帅，王开松

(1.安徽理工大学 机械工程学院，安徽 淮南 232001；2.矿山智能技术与装备省部共建协同创新中心，安徽 淮南 232001)

随着煤矿机械研究的不断深入，煤矿机械一体化、机械化、智能化水平日益提升[1]，致使煤矿开采速率大大提高；煤矿上的通风系统、排水系统等都需要安装管道，所以管道安装需求大。在此背景下，煤矿上的管道辅助安装装备就成为开采系统高效生产的短板和薄弱环节[2]。对于现有的管道安装设备而言，管道安装装备功能单一、安装效率低[3]、安装工作连续性差，不能满足煤矿开采的需求；为了满足淮南地区约4000 mm×3700 mm的矿井架管需求，本研究提出了一种煤矿综掘用机械臂式架管机设计思想。

架管机机械臂是移动、调整、安装管道的关键部分，国内外学者对机械臂的运动空间和运动轨迹等进行了较为深入的研究，侯歆岩就对五自由度的机械手进行了建模、仿真以及运动学求解[4]。孙增光等对IRB2400 机器人进行研究，不仅建立了D-H坐标系，还通过Matlab对整个手臂机器人的关节空间轨迹进行了仿真规划[5]。刘芳君完成了对FANUC ARC 100i型六轴工业机器人运动学的理论基础的分析与推导以及正逆运动学的求解过程，还提出了一种稳定性高、精度高的MPGA-RBFNN运动学求解算法[6]。

依据上述有关研究，结合淮南地区的实际工作要求，本研究对架管机机械臂进行了建模，得到了机械臂夹爪上的运动空间，验证了运动空间的合理性；用ADAMS软件完成了动力学仿真，得到了架管机机械臂在不同负载下的运动参数仿真结果，其仿真结果分析得到架管机机械臂运动状态、稳定性以及不稳定性产生的原因，相关仿真结果为架管机实际模型的搭建奠定了理论基础。

1 综掘架管机的工作原理

图1展示了综掘架管机的行走部分、调节部分、机械臂部分、执行部分、动力部分和工人平台部分，其中架管机大臂、小臂可以独立的前后摆动，通过大臂和小臂的摆动，将小臂末端的执行机构调整到指定的工作位置。

图1 煤矿综掘用机械臂式架管机整体图

架管机机械臂的运动轨迹决定了架管工作效率，所以对架管机机械臂的运动轨迹进行了分析。

2 三自由度架管机机械臂的运动分析

2.1 坐标系的建立

三自由度架管机机械臂有三个关节、三个自由度，每一个关节对应一个自由度，两个关节之间通过连杆相互连接，关节控制连杆的转动角度和速度。为了更加准确地分析连杆和相邻连杆的相对位置关系，需要给每个连杆都建立一个相对独立的坐标系，图2展示了机械臂连杆坐标系。

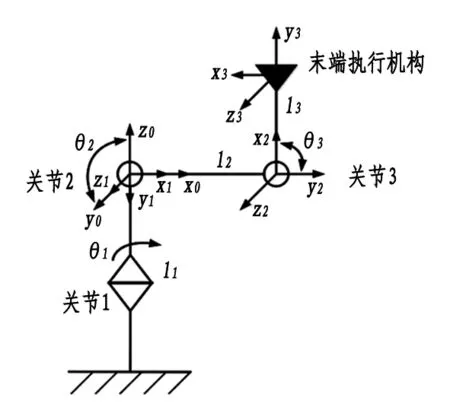
图2 机械臂连杆坐标系

在图2中，关节1是架管机的大齿轮齿条液压缸，关节2和关节3控制机械臂的俯仰。根据D-H参数法原理，每个连杆上的坐标系z轴都与旋转副的轴线重合，并且各自的方向也都相同。根据建立好的连杆关节坐标系，可以确定机械臂的D-H参数，每个连杆有四个参数表示，即连杆长度ai、连杆扭转角ai、连杆间距di、连杆关节角θi。表1展示了机械臂D-H参数。

表1 架管机机械臂D-H参数

(1)

(2)

每个相邻连杆的位置矩阵：

(3)

(4)

(5)

式中Rot(xi-1,αi-1) 表示坐标系{i-1}绕xi-1轴旋转αi-1度；

Trans(αi-1,0,0)表示坐标系{R}沿着xi-1轴平移αi-1个单位距离；

Rot(zi,θi)表示坐标系{Q}绕zi轴旋转θi度；

Trans(0,0,di)表示坐标系{P}沿着zi轴平移di个单位距离。

2.2 机械臂运动空间

根据图2进行架管机机械臂运动学正运算，可以得到机械臂末端可以达到的空间位置，位置如式(6)，图3展示了机械臂在x、y、z轴的取值。

(6)

图3 机械臂x、y、z方向取值

架管机机械臂各关节在相应的范围内运动，机械臂末端点的全体集合就是机械臂末端的运动空间[7]。已知l1=0.6 m、l2=1.1 m、l3=1 m，得到运动空间图4，机械臂运动空间图展示了机械臂可以达到的所有空间位置，将轴的空间取值与煤矿巷道实际位置对比可得，机械臂轴的空间取值可以满足架管机在煤矿巷道的架管工作位置。

图4 运动空间图

3 三自由度架管机机械臂的动力学分析

为了得到机械臂的动力学仿真结果，对即将导入ADAMS的模型进行简化，只保留架管机的机械臂部分。在SolidWorks中绘制了架管机械臂的三维模型，将机械臂部分导入ADAMS软件中进行动力学仿真，图5为架管机机械臂三维模型导入图。

图5 架管机机械臂三维模型导入图

图5中的模型已经完成了大臂、小臂转动副的连接，还对转动副施加了驱动力。

3.1 空载时架管机机械臂仿真分析及结果

根据架管机机械臂的实际运动路径对机械臂的运动方程进行定义[8]，设定运动总时间为5 s，步数为500，通过软件仿真得到了图6机械臂关节角变化曲线，图6展示了当大臂和小臂同步协同运动时，关节角θ2和θ3的变化曲线以及关节角能达到的最大值，图7展示了小臂的质心位移、图8和图9分别展示了小臂质心的速度和加速度。

动力学仿真得到了架管机小臂质心的位移变化曲线，还得到关节角θ2、θ3角度变化曲线图，图6中关节角变化曲线光滑并呈周期性变化，关节角变化周期T=4 s，θ2最大关节角达到120°，θ3最大关节角达到58°，并且关节角呈周期性稳定变化。

图6 机械臂关节角变化曲线图

图7 小臂质心位移图

图8中质心速度在y轴上呈光滑、连续的周期性变化，y轴上速度最大值为1.9 m/s；z轴上速度最大值为2 m/s，z轴上的小臂质心速度图像呈周期变化，但速度变化过程中出现速度振荡，所以架管机小臂在运动时，不稳定的速度变化可能会影响架管机机械臂整体的稳定性。而加速度的变化趋势与速度变化趋势相同，加速度、速度的曲线都呈T=8 s的周期性变化。

图8 小臂质心速度图

图9 小臂质心加速度图

3.2 夹取指定位置管道时架管机机械臂的仿真分析及结果

图10展示了模拟夹取管道的位置，根据管道的位置，对架管机机械臂运动路径的运动方程进行定义，给定关节1为固定角速度运动方程，关节2也为固定角速度运动方程，其运动时间为3-4 s。设定运动总时间为4.2 s，步数为500，通过软件仿真得到了空载时机械臂的运动分析曲线以及负载时机械臂的运动分析曲线。

空载时机械臂的相关运动曲线，依据夹管位置设定了符合条件的关节运动函数，图11展示了关节1设定的角速度变化曲线，关节1在x轴上的匀角速度为28度/秒。图12展示了关节1处转矩变化曲线，在x轴方向上，2.1 s和3.1 s处的波动是由于关节2的角速度变化导致。

图10 夹爪夹取管道位置图

图11 关节1角速度变化曲线图

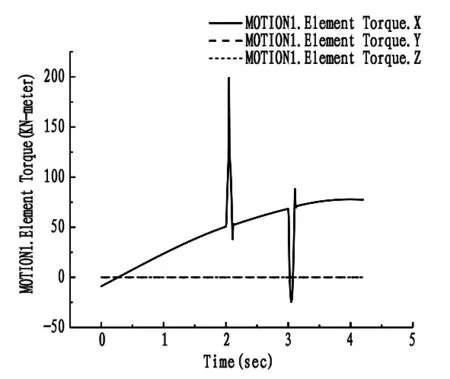
图12 关节1力矩变化曲线图

图13展示了关节2设定的角速度变化曲线，关节2以最大35度/秒的角速度在2 s到3 s之间加入架管运动。图14展示了关节2处转矩变化曲线，关节2在2.1 s和3.1 s处的波动趋势与关节1波动趋势相同，其最大峰值只有140 kN·m，关节2波动原因与关节1处波动原因相同。

图13 关节2角速度变化曲线图

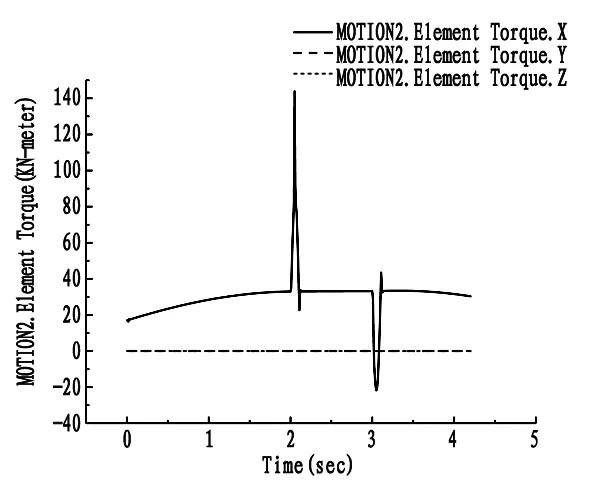
图14 关节2力矩变化曲线图

负载时机械臂的相关运动曲线，设定夹爪夹取管道的质心点作为测量点，图15展示了管道质心角速度变化曲线，图15由关节1角速度变化曲线与关节2角速度变化曲线拟合得到。

图15 管道质心角速度变化曲线图

图16、图17、图18所得相关变化曲线都基于关节1、关节2设定的运动轨迹方程。图16展示了管道质心速度变化曲线，图中曲线整体变化趋势平稳但在2-3 s间，y轴与z轴的质心速度变化曲线发生突变，突变原因是由于关节1的固定角速度运动中加入了关节2的运动，关节2的运动时间为2-3 s，其变化时间与速度变化曲线的变化趋势相吻合。

图17展示了管道质心加速度变化曲线，图中加速度的明显变化出现在2 s和3 s左右，关节2在2 s左右开始运动，3 s左右结束运动，导致加速度出现短暂且明显的变化，图17所展示的变化情况与图15、16的变化情况相对应。

图18展示了各轴线上位移变化曲线图，图中可见位移变化曲线趋势较为平稳。图17、18中在2 s和3 s处都出现明显拐点，两拐点出现都是由于关节1的匀速运动中加入关节2的运动。

仿真得到架管机关节角的角度范围，关节角的范围决定了架管机机械臂的运动空间；还得到质心的速度、加速度等，质心的速度、加速度表明了不同负载情况下的架管机运动的稳定性，其分析结果都是搭建架管机实物的理论依据。

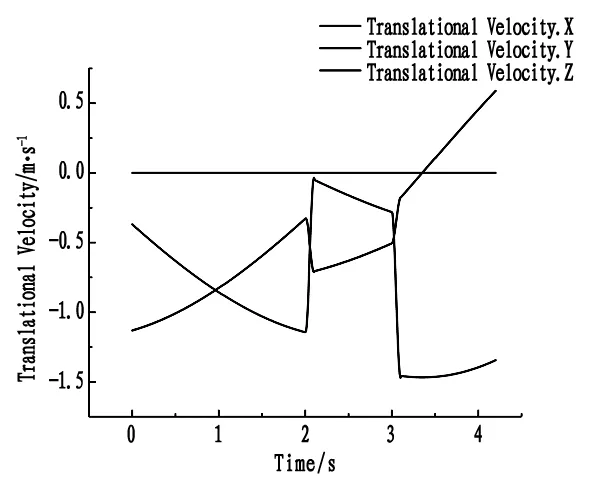
图16 管道质心速度变化曲线图

图17 管道质心加速度变化曲线图

4 结论

通过对架管机机械臂的运动分析和动力学仿真分析，结论如下：

以机械臂的三自由度连杆坐标系为基础，求解得到了机械臂z轴运动空间的最大值为2.6 m，此高度可以满足淮南地区实际架管需求。

当不指定管道夹取位置时，架管机小臂z轴的最大质心速度为2 m/s，在T=8 s的周期变化中会产生不稳定速度波动；速度、加速度曲线变化趋势相同，关节角曲线变化稳定，θ2、θ3的最大值分别是120°和58°。

当指定管道夹取位置时，关节1、关节2为固定角速度运动，关节1的力矩能达到200 kN·m的最大值，关节2的力矩能达到最大值为140 kN·m。

ADAMS动力学仿真得到了架管机的位移、速度、加速度等变化曲线，其表明架管机机械臂运动状态、稳定性以及不稳定性产生的原因，相关仿真结果为架管机实际模型的搭建奠定了理论基础。