基于格基规约的线性检测改进算法

2021-04-07江晓林董春秀

黑龙江科技大学学报 2021年2期

江晓林，董春秀

(黑龙江科技大学电子与信息工程学院，哈尔滨 150022)

0 引言

近年来，多输入多输出(Multiple input multiple output，MIMO)[1]技术的新型无线通信系统在各界得到广泛研究与利用。多输入多输出技术通过多径效应来取得对传输系统的有利条件，从而得到分集和复用增益，使系统抗干扰能力和信道传输的可靠性得到进一步提升。因此,MIMO无线通信系统能够在不增加带宽的条件下有效提高频谱资源的利用率，使能量效率也得到数量级的增加。虽然MIMO技术能够传输大规模数据，但是也面临在接收端可靠检测信号的挑战。

目前，在MIMO系统中，主要研究的信号检测算法大致可以分为非线性与线性[2]。非线性检测算法主要有连续干扰消除(Successive interference cancellation，SIC)、球形检测(Sphere detection，SD)；线性检测算法主要有迫零检测(Zero forcing，ZF)、最小均方误差检测(Minimum mean square error，MMSE)、最大比合并检测(Maximal ratio combining，MRC)。ZF算法因为存在矩阵求逆等过程，也没有考虑到噪声对信号的影响，复杂度会高一些。相比之下，MMSE检测算法考虑到噪声对传输信号的影响，检测性能较ZF优越。MIMO系统信号检测算法的性能和复杂度之间成正比例关系，提高系统的检测性能，相应的也增加了检测的复杂度。

格基规约[3]作为一种信号检测前的预处理方法，以增加少量的复杂度来减少信道矩阵条件数，获得性能较好的规约基，提升系统的检测性能。由A.K Lenstra提出的LLL规约等[4]，能够使系统检测性能提高的同时，拥有较低的复杂度。笔者将传统ZF、MMSE算法与格基规约中的LLL算法相结合，寻找最优的信道矩阵，对其中多个初始基进行约减，得到正交性更好的一组等效基，以提升MIMO系统的信号检测误码率性能，获得最佳的检测效果。

1 系统模型

图1为一个典型的MIMO系统模型。假定基站发射端拥有Nt个发射天线，用户接收端有Nr个接收天线，且Nt≥Nr。输入的信号经过发射机进行编码、加密和调制等处理，通过发送端的多根天线将调制之后的信号发射到无线信道中，利用电磁波传输到接收端，接收端接收到的是多路信号的叠加，接收机要通过有效的解调、解码和译码等处理恢复出原始的输入信号。

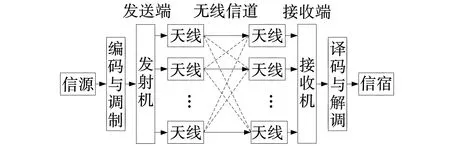
图1 MIMO系统模型

一般在讨论MIMO检测算法时，常常将图1中的单链路MIMO系统结构框图转换为图2的检测结构。

图2 MIMO检测模型

与之对应的等效数学模型[5]为：

y=Hx+z，

式中:H——Nr×Nt的信道矩阵，H中的每个元素从其发射天线到对应接收天线的信道增益；

x——Nr×1每个符号周期的发射信号矢量；

z——均值为0，方差为σ2的高斯白噪声，z=(z1,z2,…,zNr)T。

2 传统线性检测算法

线性检测方法[6]将来自目标发射天线的期望信息流作为有用信息，同时将其他发射信号当做干扰。在检测来自目标信号发射天线的期望信号的过程中，要最小化或消除来自其他发射天线的干扰信号。基本的线性检测方法包括ZF检测和MMSE检测。

2.1 ZF检测

ZF检测算法的核心是通过滤波矩阵对接收信号的信号向量进行滤波，达到完全消除多个天线发送的符号间干扰的目的。

ZF的加权矩阵为

GZF=(HHH)-1HH，

从而得到，发送信号x的估计值公式为

(1)

式中,HHH——H的共轭转置矩阵。

由式(1)可以看出，ZF检测算法完全消除发送信号间干扰，但HHH的矩阵求解复杂度高，在检测过程中很容易过度放大被检测的信号的噪声，导致检测结果产生误差，ZF估计误差为

(2)

2.2 MMSE检测

MMSE检测算法[7]的核心是使检测出来的信号与实际发送的信号的均方误差值达到最小。它是基于ZF检测算法噪声增强问题提出的检测算法，降低了噪声对信号检测的影响，提高检测的性能。

GMMSE=argGmin{E‖Gy-x‖2}。

(3)

式(3)达到最小，求出GMMSE，对E‖Gy-x‖2求梯度得

GMMSE=(HHH+σ2I)-1HH，

得到发送信号x的估计值公式为

MMSE算法的估计误差为

(4)

比较式(3)(4)可知，随着噪声功率增大，MMSE算法检测性能要比ZF算法要好，因为MMSE算法考虑天线间干扰的消除，也考虑噪声对接收信号的影响，寻求发送信号与估计信号总误差率最小化，比ZF算法检测性能要好。在MIMO系统中，信道矩阵的条件数过大会对信道的容量和算法检测性能造成负面影响。若信道矩阵的条件数非常大会增加噪声在传输过程中的影响，使算法检测性能下降，相反，如果信道矩阵的条件数减少，MMSE检测的性能也会随之提高，减少信道矩阵的条件数极其关键。

3 LLL改进的线性检测算法

图3为格基规约检测模型，与图2相比，信道矩阵增加了格基规约的过程。即：

T——单位模矩阵。

图3 格基规约检测模型

接收信号y通过滤波器，把滤波矩阵G乘以接收信号y得

r=Gy=H+y=T-1x+H+z=d+w，

式中:G——滤波矩阵；

w——噪声分量；

d——原始信号x经过格基规约变换后的信号矢量。

此时，不能将x作为判决量，而是将x变换后的d作为判决量，可以表示为：

(5)

式中,Q(H+y)——在星座图上对检测信号进行硬判决。

通过对信道矩阵的此类约减变换，接收端信号检测时判决点距离检测边界的最小距离会变长，从而减少误码率，实现对MIMO通信系统性能的改善[9-10]。

4 仿真结果与分析

4.1 约减参数的选取

仿真工具为Matlab软件，MIMO系统天线选用4×4的配置，信号采用QAM调制方式,信道噪声为均值为0、方差为σ2的高斯白噪声，约减参数应遵循1/4

图4 0～10 dB下MMSE-LLL算法不同M取值的误码率曲线

信噪比范围为10～20 dB时，MMSE-LLL算法在不同约减参数M取值下的性能仿真曲线，如图5所示。

图5 10～20 dB下MMSE-LLL算法不同M取值的误码率曲线

由图4可知，在0～10 dB时，不同约减参数的取值对MMSE-LLL算法误码率影响几乎没有影响。由图5可知，在10～20 dB时，约减参数越小，算法误码率相对较高，约减参数越大，算法误码率相对较低，总体变化不大。在实验过程中，约减参数用来控制降格基的质量，从总体来看其对运算复杂度的影响较小，一般取M=0.75。

4.2 传统与改进算法的比较

仿真工具为Matlab软件，MIMO系统天线分别选用2×2、4×4、6×6三种不同的配置，信号采用QAM调制方式,信道噪声为均值为0、方差为σ2的高斯白噪声，约减参数M=0.75。

信噪比范围为0～20 dB时，MRC、ZF、MMSE和ZF-LLL、MMSE-LLL算法在不同收发天线数下的性能仿真曲线，如图6所示。

图6 不同检测算法误码率曲线

由图6可知，ZF-LLL、MMSE-LLL检测算法误码率明显低于传统MRC、ZF与MMSE算法。随着收发天线数目的增加，线性改进算法与传统线性算法性能的差异越来越明显，误码率更加优越。这是由于在收发天线数目增加时，系统可以获得更多的空间自由度，提供更多的分集增益，使系统的抗噪声性能增强，误码率降低，信号传输性能越好。