例说用特殊化方法探求定值
2021-04-06李润林
李润林


【摘要】在某些几何图形中,有些点或直线(射线、线段)的位置是不断变化的,在这个变化过程中,有一些位置关系(如两直线的平行或垂直)或数量关系(如线段的长度、角的大小、弧的大小、线段的比等)却始终保持不变,这就是几何中的定值问题.
【关键词】特殊化方法;探求定值
图1例1 已知:如图1所示,在△ABC中,AB=AC,P是BC上任意一点,PR⊥AB,PQ⊥AC,BD⊥AC,垂足分别为R,Q,D.求证:PQ+PR为定值.
分析 因为P是BC上任意一点(即P是动点),所以当P运动到B的位置时,R和Q也随之分别运动到B和D的位置,此时PR=0,PQ=BD,由此猜想BD就是所要求的定值.
下面我们来证明这个猜想在一般情况下也是正确的.
分析 因为P是△ABC内任意一点(即P是动点),所以当P运动到△ABC的重心位置时(图7),由“等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合”及“角平分线上的点到已知角两边的距离相等”知PD=PE=PF=1[]3AD,于是我们猜想PD+PE+PF=AD=3[]2m就是所要求的定值.
分析 当正方形A1B1C1O绕点O旋转到特殊位置(图10)时,容易证明重叠部分是一个边长为1[]2的小正方形,其面积为1[]4,由此我们猜想图9中重叠部分四边形OEBF的面积等于1[]4就是所要求的定值.
下面我们来证明这个猜想在一般情况下也是正确的.
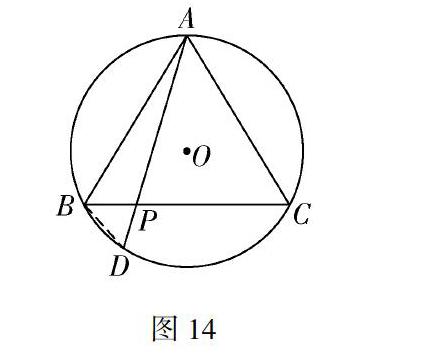
分析 由于点P是BC边上的一个动点,所以当点P运动到BC的中点位置(如图13)时,由AB=AC、“等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合”及“垂径定理”的推论知AD是⊙O的直径,且∠APB=90°.连接BD,则易证△APB∽△ABD,于是AP[]AB=AB[]AD,從而猜想AP·AD=AB2就是所要求的定值.
下面我们来证明这个猜想在一般情况下也是正确的.
综上所述,在求解几何定值问题时,确定定值等于多少是解决问题的关键,其一般方法是:通过分析特殊位置情况下的图形先猜想出定值,然后在一般的位置情况下证明猜想成立.也就是说,解决定值问题一般有如下两个步骤:
(1)在特殊位置下探求定值;
(2)在一般情况下证明结论.
