基于表面风压分析的分离式双箱梁流场特性研究
2021-04-06李加武朱长宇
李加武,朱长宇
(长安大学公路学院,陕西西安 710064)
0 引 言
近年来,分离式双箱梁在大跨径桥梁中的应用越来越广泛。对于流线型闭口单箱梁断面来说,虽然开槽宽度对断面颤振稳定性的变化规律存在分歧,但不可否认的是,合理地设置中央开槽能够提高颤振临界风速[1-2]。分离式双箱梁相较于传统闭口单箱梁,其颤振稳定性更为优越[3-5]。然而,分离式双箱梁的涡振性能却逊色于闭口箱梁[6]。涡激振动虽不会破坏桥梁结构,但由于其多发生在低风速下,易引起桥梁构件疲劳破坏,降低了行车舒适性[7-10]。国内外对于箱梁断面的涡振成因及抑制措施的研究较多[11-13],对分离式双箱梁涡振成因及抑振措施开展的研究相对较少。改变分离式双箱梁空隙比,其Strouhal数也随之改变[14-15];在各抑振措施中,中央格栅可以将分离式双箱梁上游侧中央开槽处形成大尺度的、有规律性脱落的旋涡划分为细小旋涡,从而抑制中央开槽处大尺度旋涡的形成,达到抑制涡振发生的目的,是较为有效的手段[16-17]。分离式双箱梁涡脱受上游尾流激振及下游涡脱引起的紊流共同影响[15],空隙处形成的旋涡随着涡振振幅的增大而增强;对于分离式双箱梁的竖弯涡激共振,下表面外围间隙附近各测点所采集风速的主频与竖弯基频相等[18-19],即分离式双箱梁竖弯涡振时,其下表面间隙附近受涡脱作用的影响。扭转涡振相较于竖弯涡振,对风攻角更加敏感[20],对于分离式双箱梁扭转涡振时涡脱作用范围分布有待研究。在不同雷诺数条件下,分离式双箱梁表面平均风压分布与脉动风压分布会产生明显变化,并且裸梁断面更容易产生涡脱,受雷诺数影响有限[21]。因此,裸梁断面对雷诺数效应较不敏感,对于研究分离式双箱梁的涡振更具代表性。在近似攻角下风洞试验与实测所得到的表面平均风压系数分布趋势一致[22]。对于分离式双箱梁断面,讨论其表面平均风压系数分布具有实际工程意义。
本文以某分离式双箱裸梁断面节段模型为研究对象,分析分离式双箱梁扭转涡振锁定区间内外涡脱作用影响范围的变化规律及不同状态下分离式双箱梁风压分布特征,为工程实践提供参考。
1 分离式双箱梁模型参数及测点布置
在分离式双箱梁断面周向布置38个测压点,通过固定于模型内部的电子压力扫描阀以312 Hz采样频率同步测量每个测点所受的风压。测点布置及断面尺寸如图1所示,其中将测点横向分布位置量纲一化,其中B为模型梁宽度,X为坐标轴对应测点位置,C1,C2,P为测点。
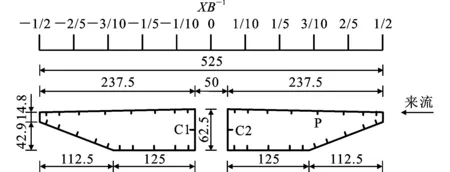
图1 分离式双箱梁测点布置(单位:mm)
2 振动状态下分离式双箱梁风压分布
2.1 分离式双箱梁的扭转涡振
在振动状态时,节段模型缩尺比为1∶40的风洞试验参数如表1所示。
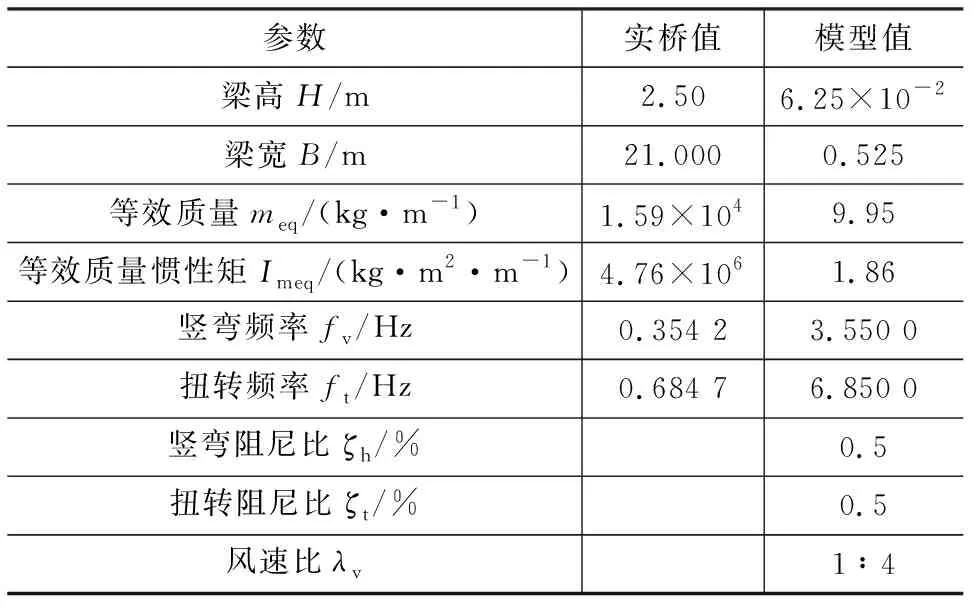
表1 分离式双箱梁节段模型试验参数Tab.1 Segmental Model Test Parameters of Separated Twin-box Girder
分离式双箱梁断面仅在3°攻角下产生扭转涡振,模型振幅如图2所示。当风速为3.6 m·s-1时,扭转振幅出现了峰值,同时竖弯振幅也出现了较小的峰值;当风速为6.5 m·s-1时,竖弯振幅出现了一个较大峰值,但其振幅变化并不显著。因此,该分离式双箱梁模型产生了以扭转为主的涡振。对分离式双箱梁时程进行频域分析,得到在该风速下其扭转涡振的卓越频率,以风速为3.6 m·s-1时分离式双箱梁振动扭转时频分析为例(图3)。在3.4~4 m·s-1的风速区间内,其扭转振动频率与模型扭转基频相等,模型振动出现了“锁定”现象。3.4~4 m·s-1为该分离式双箱梁的涡振锁定区间。
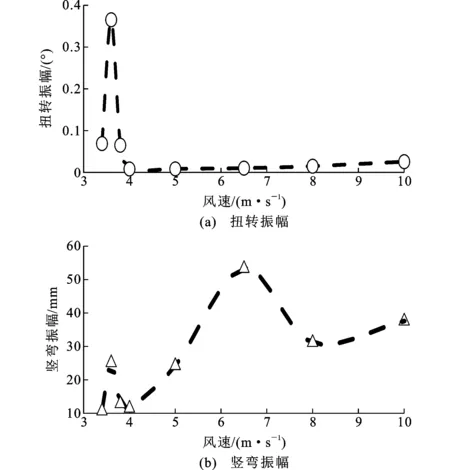
图2 分离式双箱梁模型不同风速下的振幅
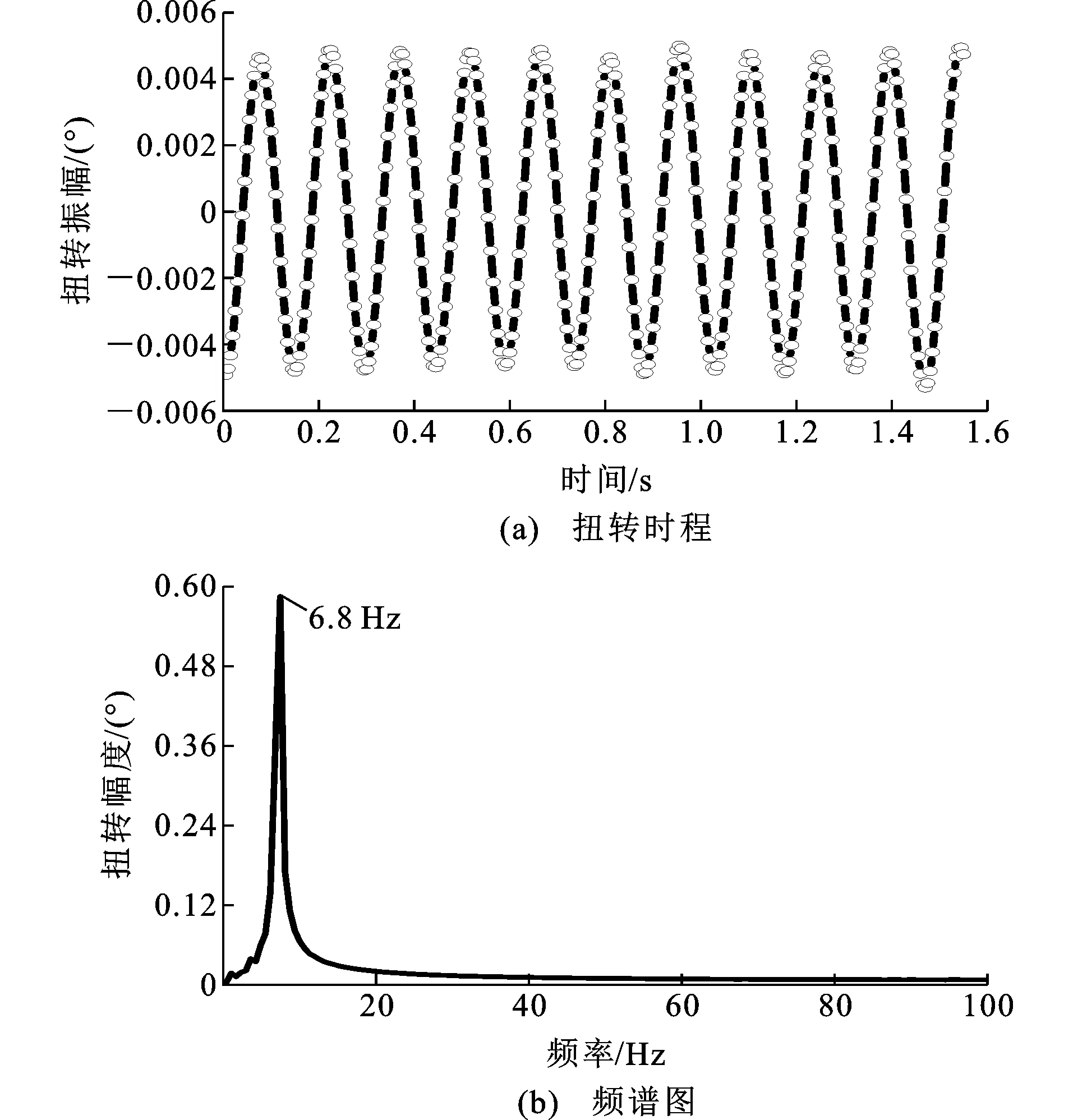
图3 3.6 m·s-1风速下模型扭转时程及频谱图
2.2 振动状态下分离式双箱梁各测点风压分布特性
分离式双箱梁空隙内侧交替形成的大尺度旋涡同主梁后侧箱体碰撞会产生相应的周期性作用力,当作用力的频率与结构固有频率一致时即可能激发振幅较大的涡激共振[23]。压力脉动[24-26]为压力作用在某个部位集中,且有可能呈现周期性的现象,常用于水利及航空方面的分析研究;分离式双箱梁表面也会因流场环境差异及旋涡脱落等原因,令风压作用不均匀或者呈现周期性,这对分离式双箱梁表面风压分析有一定的参考意义。为方便表述,将分离式双箱梁模型表面风的压力脉动主频简称为风压主频。通过对分离式双箱梁风压进行时频分析可得到作用力频率与结构固有频率一致的区域,即其激发涡振时空隙内侧产生的涡脱作用范围。
3.4~3.8 m·s-1处于分离式双箱梁涡振锁定区间内,其风压主频分布如图4所示。3.4 m·s-1为涡振振幅上升阶段,其风压主频分布较为连续,且在该风速下,分离式双箱梁顶板、空隙内侧以及底板中部区域的风压主频与模型扭转基频相近,即在该风速下,这些区域受到了涡脱作用的影响。3.6
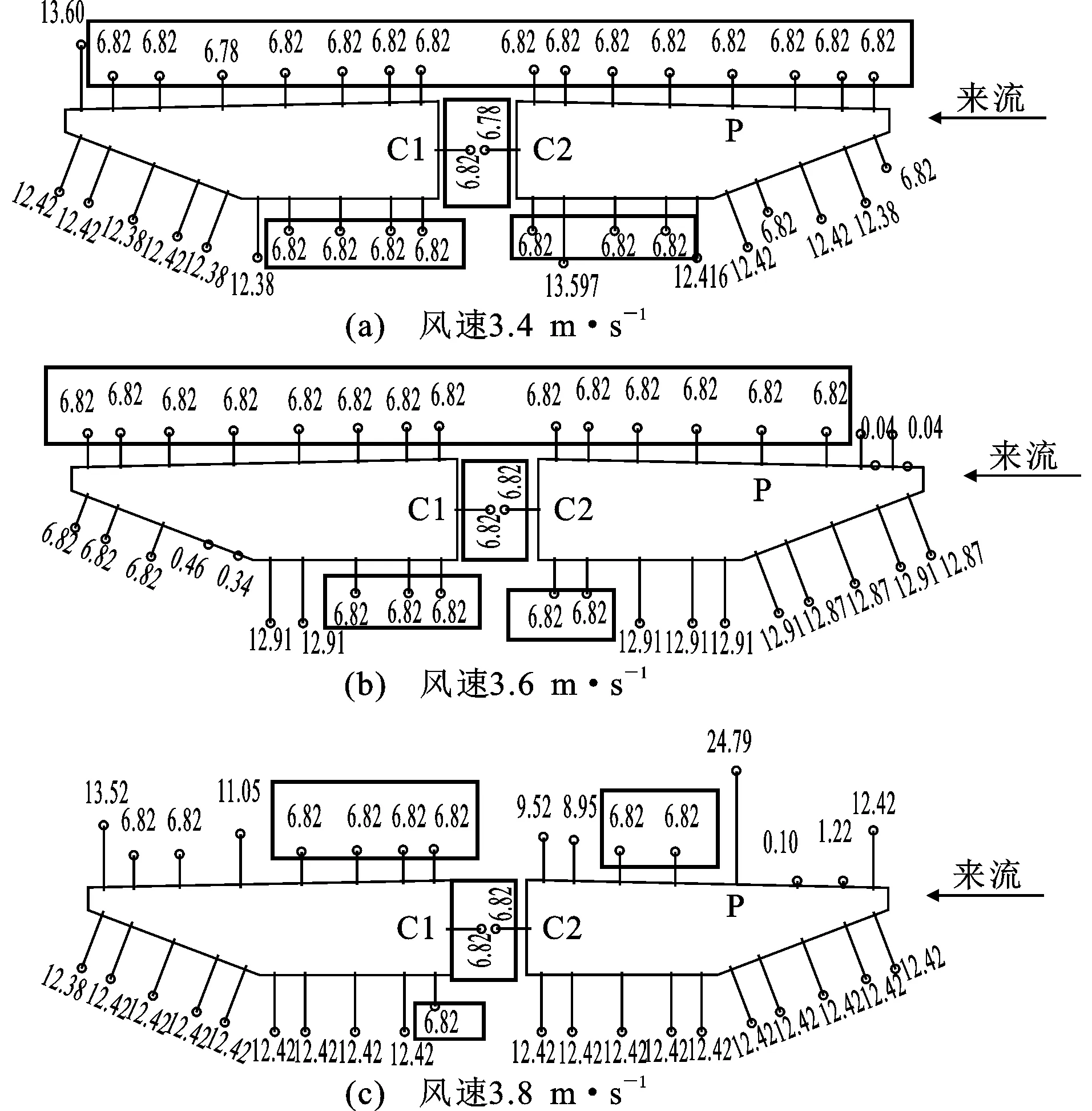
图4 3.4~3.8 m·s-1风速下风压主频分布(单位:Hz)
m·s-1为涡振振幅最大阶段,其风压主频与模型扭转基频相近的区域与振幅上升阶段基本保持一致,下表面风压主频与模型扭转基频相近的区域缩小;3.8 m·s-1为涡振振幅下降阶段,在该风速下,分离式双箱梁上表面及下表面风压主频与模型扭转基频相近的区域继续缩小,此时分离式双箱梁上表面大部分区间风压主频产生了较大变化(例如测点P风压主频升高)。因此,在分离式双箱梁涡振产生后,空隙处涡脱作用在顶面及底面的范围随着风速的提高逐渐向空隙处缩小。
在涡振锁定区间的不同阶段内,分离式双箱梁空隙内侧风压各频率上对应的能量分布也有差异。测点C1,C2为分离式双箱梁空隙内侧中心处测点,涡振区间内的风压时程及功率谱密度如图5所示。由图5可知:在涡振区间内,分离式双箱梁下游空隙处风压幅度较大;上下游空隙中心能量集中于结构扭转基频处,但上游低频及高频段能量分布较为均匀,下游主要集中在低频段附近;随着风速的改变,在涡振振幅下降阶段,空隙内侧风压在结构扭转基频处集中的能量降低。
分离式双箱梁在扭转涡振锁定区间内外的风压主频分布见图6。4 m·s-1为该模型扭转涡激共振区间的终止点,其空隙内侧的风压主频与模型扭转基频不再保持一致,但其风压主频分布依旧具有连续性,在该风速下仍有小幅度扭转振动。在6.5 m·s-1风速下,分离式双箱梁模型有一较小的竖向振动峰值,而其表面风压主频仍然保持连续,这与该风速下模型的振幅有一定关系。在8 m·s-1风速下,其风压主频分布的连续性消失。涡振区间内,分离式双箱梁的涡脱作用从空隙处及空隙外侧周围的顶面和底面随着风速提高而向内收缩;当风速超出涡振锁定区间时,分离式双箱梁上表面及空隙中心处涡脱频率超出分离式双箱梁扭转基频,空隙内侧形成旋涡的作用力频率不再与结构固有频率一致,扭转涡振消失。
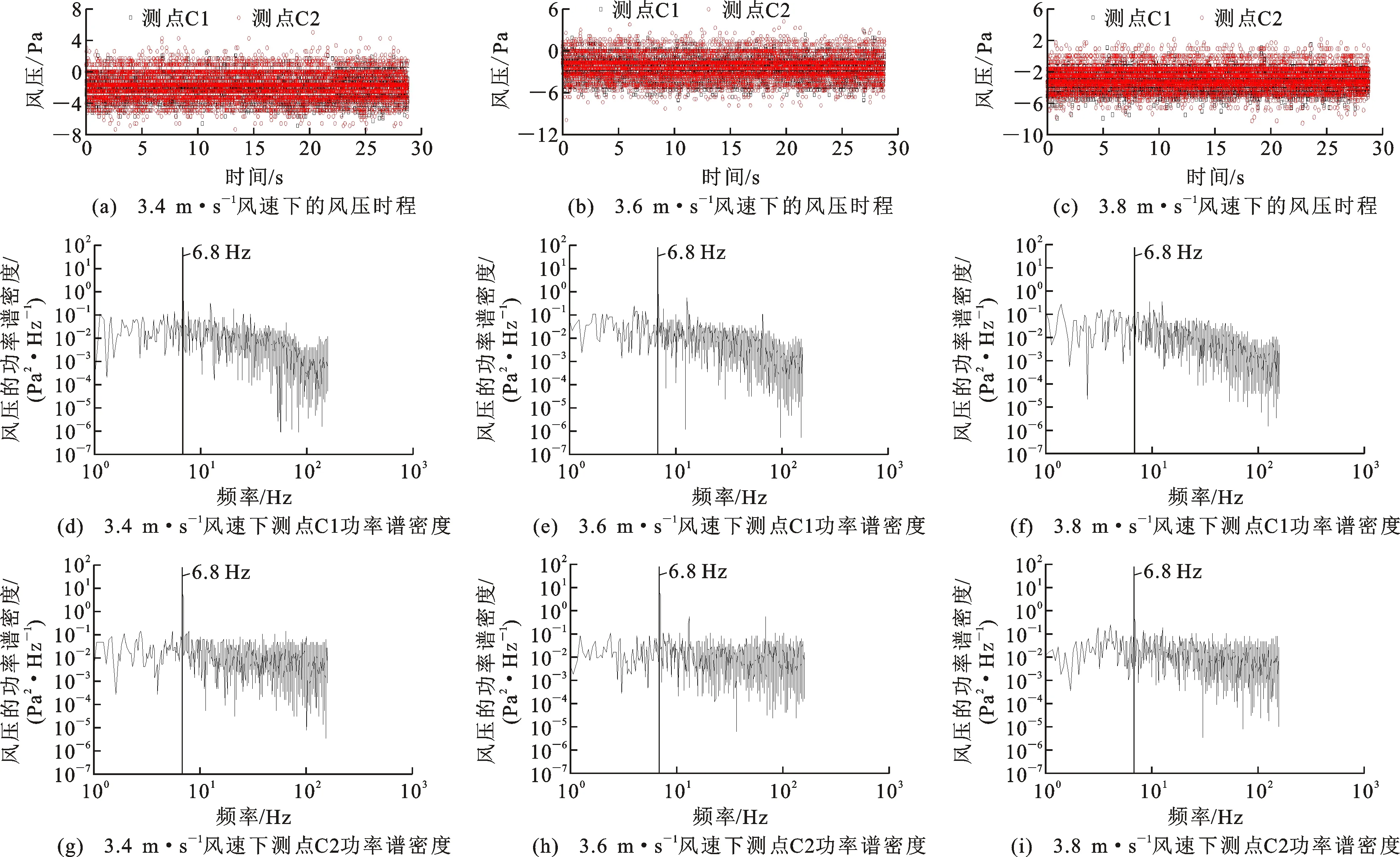
图5 3.4~3.8 m·s-1风速下测点C1,C2风压时程及功率谱密度
上述试验现象证明了分离式双箱梁空隙内侧风压主频与扭转基频保持一致是其产生涡激共振的必要条件,那么改变其空隙内侧流场特性便有利于抑制该类型断面的扭转涡振。以某分离式双箱梁节段模型风洞试验检验该结论的准确性,检验模型缩尺比为1∶70,基本参数如表2所示。

表2 检验模型参数Tab.2 Parameters of Testing Model
图7为原断面及改造后断面。在分离式双箱梁中央处设置一矩形柱,改变其空隙内侧流场环境。试验结果如图8所示,在中部增加足够尺寸的矩形柱,改变了其空隙内侧的流场环境,抑制了分离式双箱梁的扭转涡振,并且使其竖弯涡振振幅减小,竖弯涡振锁定区间后移。因此,对于分离式双箱梁的扭转涡激振动,可以增加气动措施,令其空隙内侧的流场环境改变,以达到抑制扭转涡振的目的。
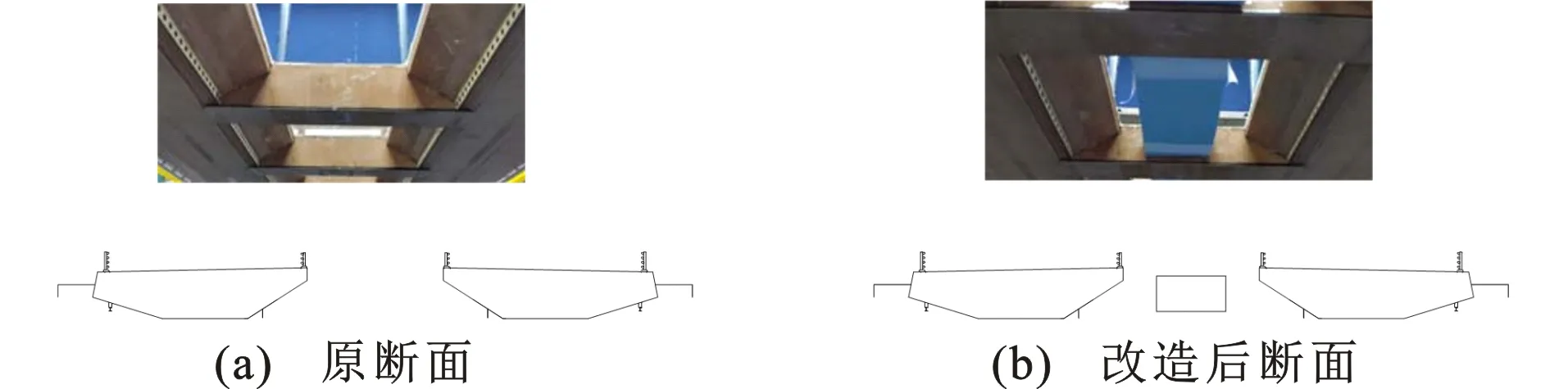
图7 原断面及改造后断面
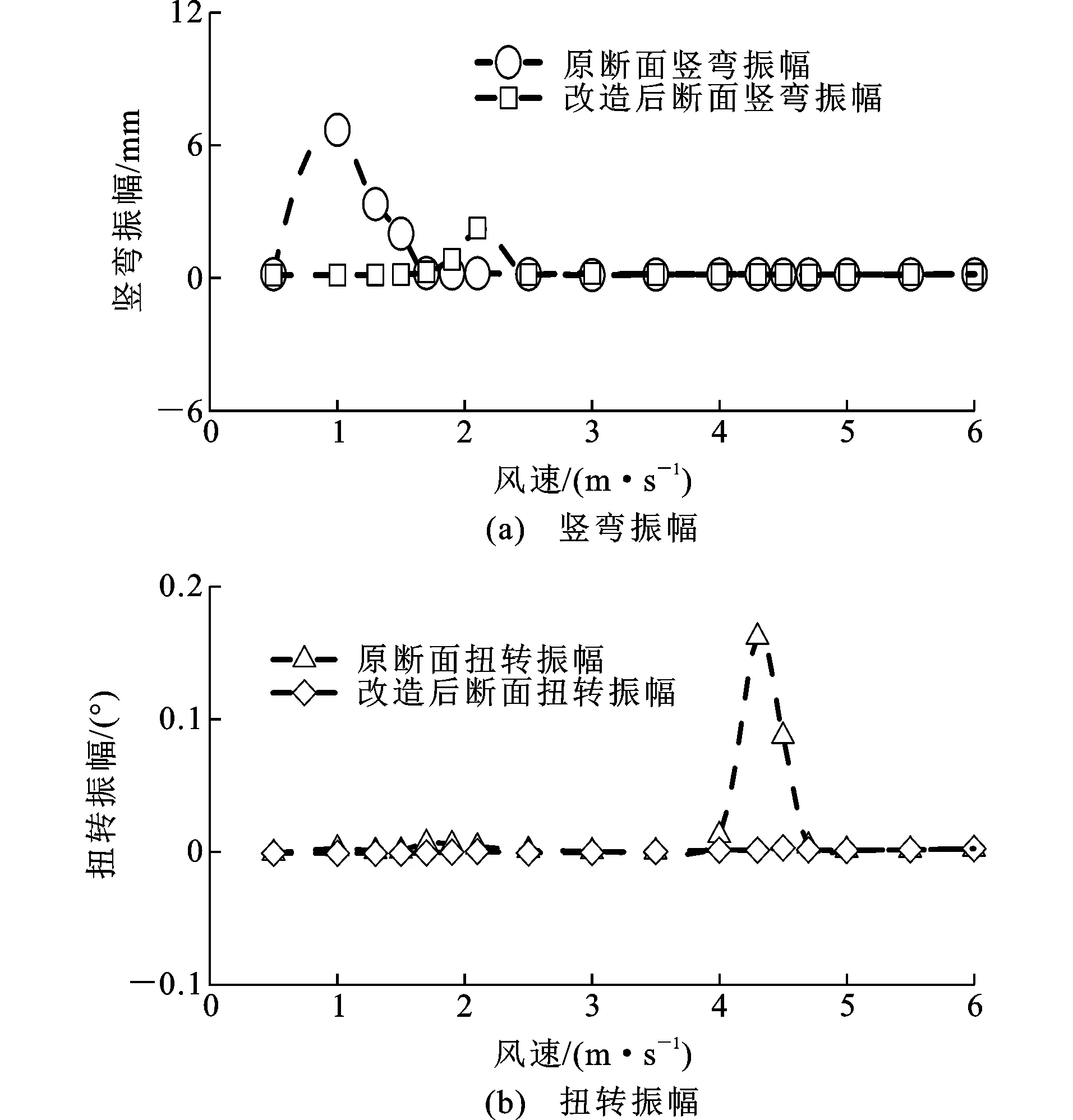
图8 节段模型各风速下振幅
2.3 涡振锁定区间内分离式双箱梁各测点表面平均风压系数
3.4~4 m·s-1为该分离式双箱梁模型的涡振锁定区间,各测点表面平均风压系数如图9所示。在涡振锁定区间内的不同阶段,分离式双箱梁表面平均风压系数变化规律一致,各风速下其上下表面压差接近。当该分离式双箱梁模型扭转振幅达到最大时,其表面平均风压系数与涡振锁定区间内其他阶段的表面平均风压系数产生了明显的偏移,上游下表面斜腹板处负压区扩大。因测点较少,只能较为粗略地表示来流在分离式双箱梁周围的分离与再附着位置。在分离式双箱梁涡振锁定区间内的不同阶段,其分离与再附着位置相同:来流在分离式双箱梁模型上表面X/B=±0.44,±0.31,-0.39,-0.23及下表面X/B=0.23,-0.30,-0.34,-0.39附近发生分离与再附着。
在涡振锁定区间内的不同风速下,各测点平均风压系数近似服从正态分布, 以3.4 m·s-1风速下各测点平均风压系数分布为例,结果如图10所示。
Z-score可以真实反映一个分数距离平均数的相对标准距离。当样本量较小时,样本的增加会减小偏度值和峰度值的标准差,相应的Z-score会变大,会给正确判断样本数据的正态性情况造成一定的干扰。因此,在数据较少的情况下,分别计算偏度和峰度的Z-score,利用变量的偏度和峰度进行正态性检验来判断样本的正态分布性比较合理。分别对3.4,3.6,3.8 m·s-1风速下各测点的表面平均风压系数进行正态分布检验,计算结果如表3所示。查正态分布表可知,在显著性水平α=0.64%的检验水平下,Z(α)=2.73。由表3可知,偏度Z-score和峰度Z-score均满足假设Z-score小于2.73,故在α=0.64%的检验水平下认为不同测点的表面平均风压系数服从正态分布。
3 固定状态下分离式双箱梁风压分布
3.1 固定状态下分离式双箱梁各测点风压主频
在不同风速下,分离式双箱梁外侧周向各测点风压主频如图11所示。同一风速下,各测点风压主频基本保持一致,风压主频并非随着风速的提高而逐渐增大。固定状态的风压主频分布与振动状态不同,其包含能量最高的频段较为一致。从风压主频分布的角度较难使分离式双箱梁固定状态与振动状态的流场特性产生联系。
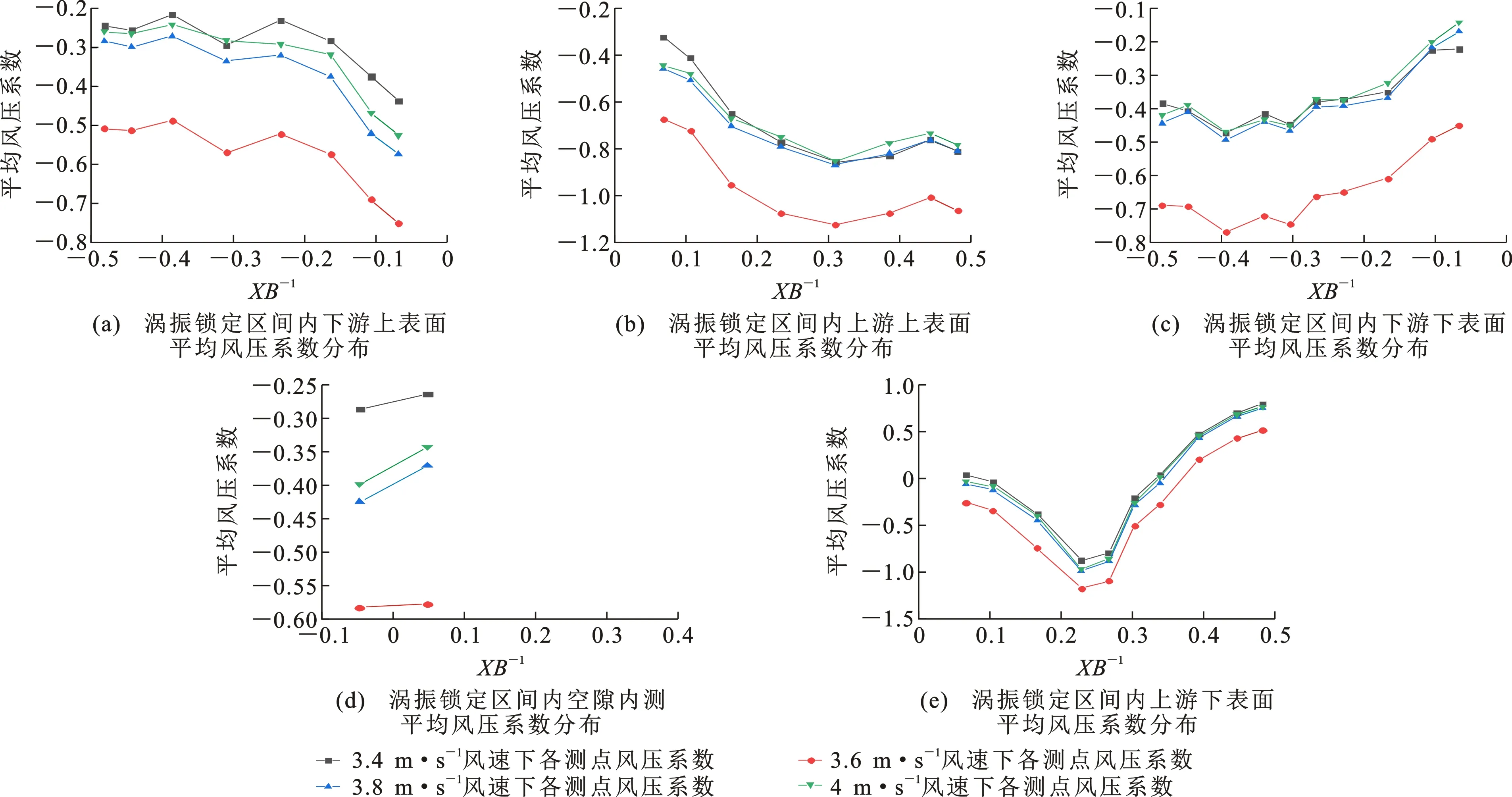
图9 涡振锁定区间内平均风压系数分布
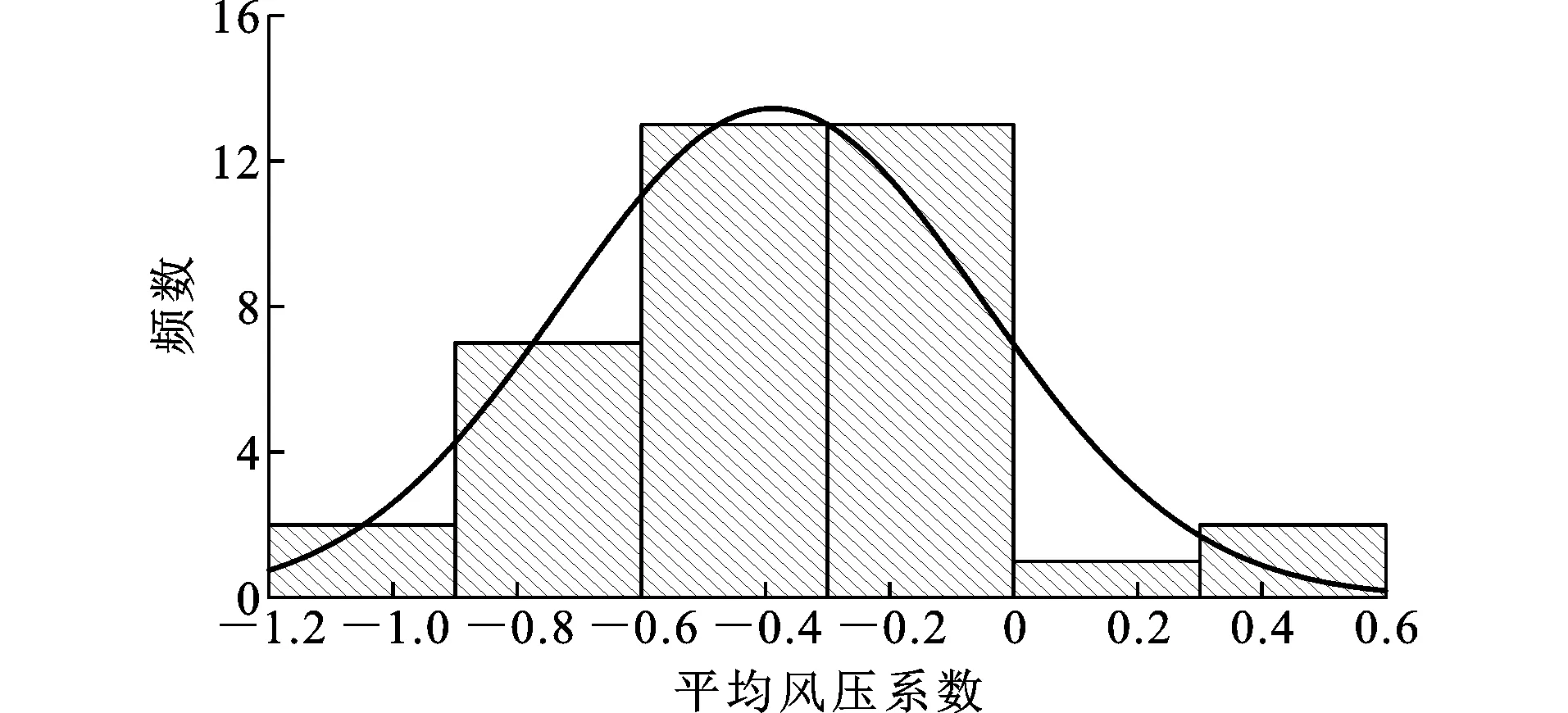
图10 3.4 m·s-1风速下平均风压系数
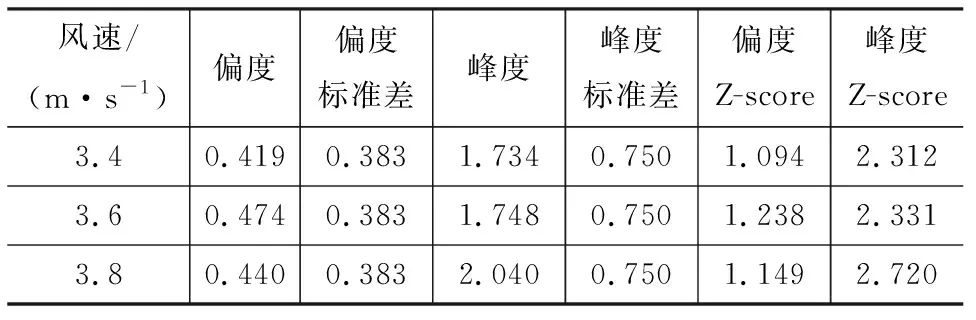
表3 各测点平均风压系数的偏度与峰度Tab.3 Skewness and Kurtosis of Each Test Point’s Mean Wind Pressure Coefficient
3.2 固定状态下分离式双箱梁表面平均风压系数
分离式双箱梁外侧周向各测点风压系数如图12所示。在不同风速下,分离式双箱梁表面平均风压系数变化较为一致;下表面尾流区X/B<0.23的区间内其分离与再附着点发生变化。在不同风速下有固定的分离点:对于分离式双箱梁上表面,来流在分离式双箱梁上表面X/B=±0.44,±0.39,±0.31,±0.23及下表面X/B=0.27,-0.11,-0.17,-0.23附近发生分离与再附着。
风速4 m·s-1处于该分离式双箱梁模型扭转涡振终止点,在该风速下,将其振动与固定状态进行对比,结果如图13所示。由图13可知,2种运动状态的上游下表面风压系数基本相同,空隙内侧以及尾流区风压系数变化趋势不同,数值上也存在较大差异。由此可见,在固定与振动状态下,分离式双箱梁上游下表面流场环境差别较小,未受到分离式双箱梁运动状态的影响。除该部分外,分离式双箱梁的上游上表面、空隙内侧及整个下游区域的风压系数分布都受到了运动状态的影响。因此,分离式双箱梁上游下表面风压作用对其运动状态的变化不敏感,对其涡振影响较小。
4 结语
(1)分离式双箱梁空隙内侧的涡脱是其产生扭转涡振的必要条件,改变分离式双箱梁空隙内侧流场环境有助于抑制其扭转涡振。
(2)在分离式双箱梁的扭转涡振锁定区间内,其表面平均风压系数服从正态分布且变化趋势一致;空隙内侧涡脱在上下表面的作用范围随着风速的提高而缩小。
(3)分离式双箱梁上游下表面平均风压系数受运动状态的影响较小。可以根据其固定状态时所得平均风压系数大致推测出分离式双箱梁起振时上游下表面的受力特征。
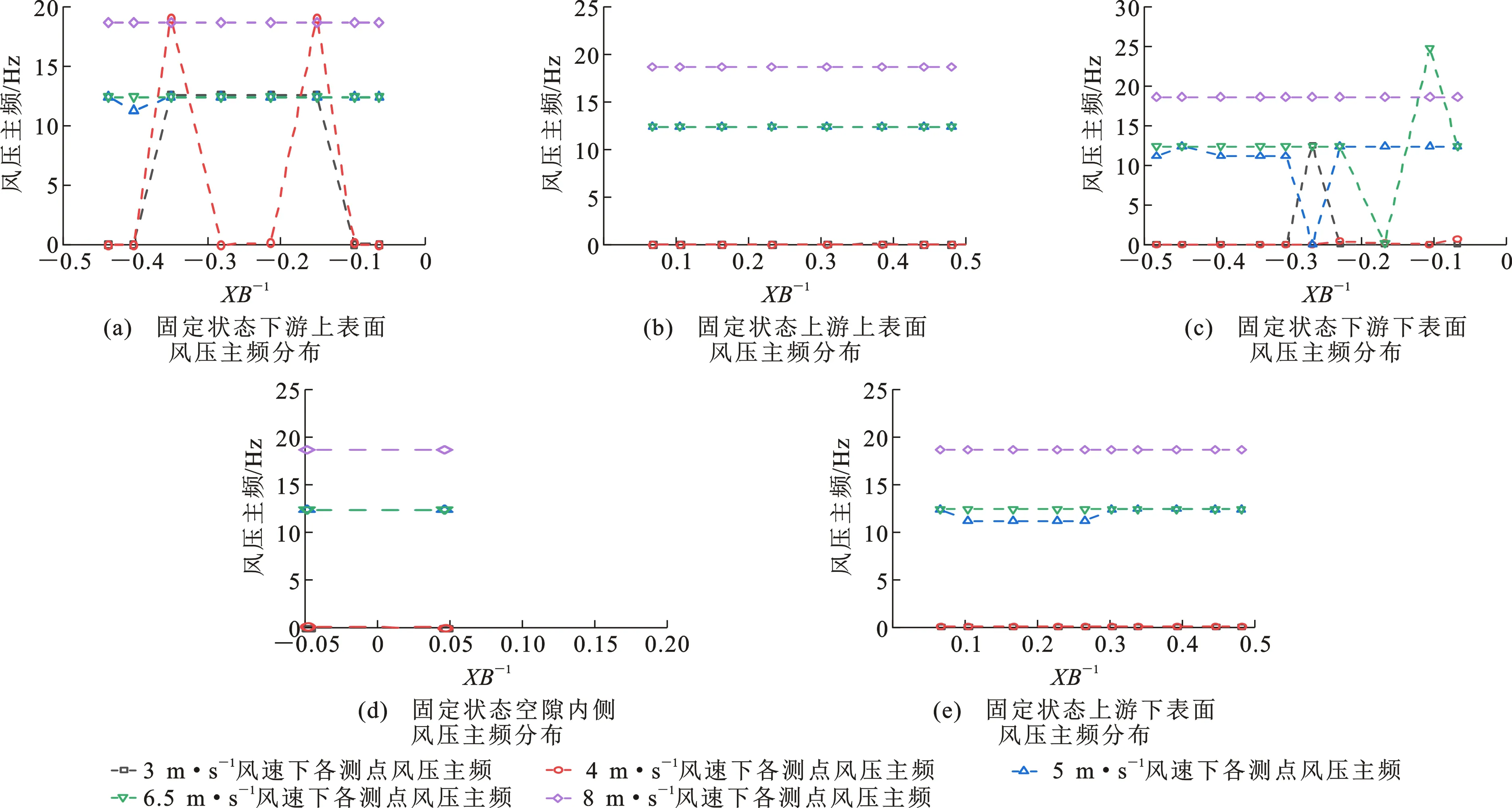
图11 固定状态不同风速下风压主频分布
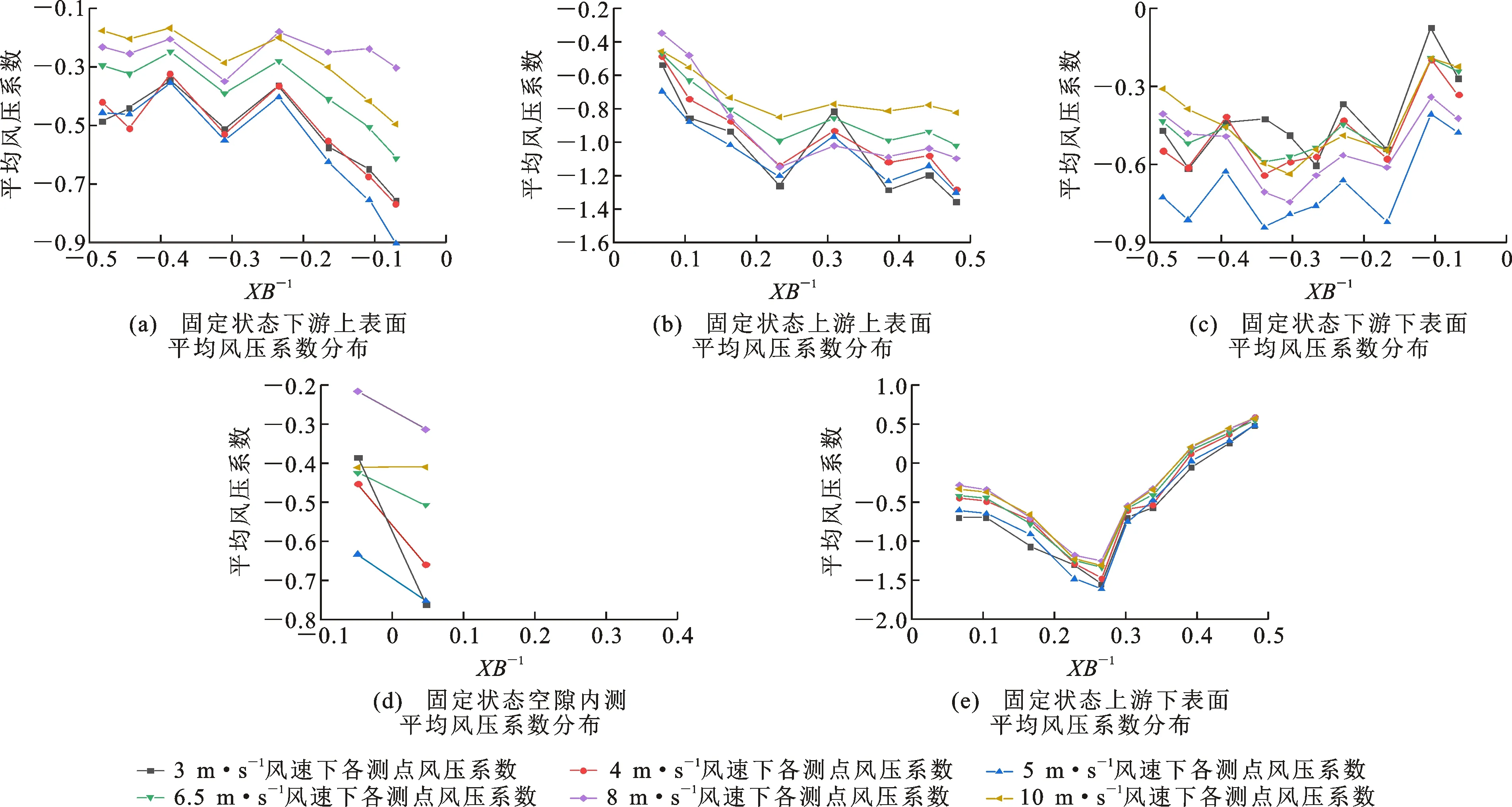
图12 固定状态不同风速下平均风压系数分布
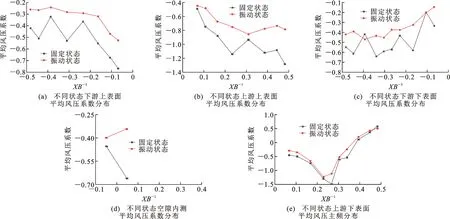
图13 不同状态4 m·s-1风速下平均风压系数分布
