局部可更换钢框架梁-柱节点受力性能研究

郑 宏，方贤禄，苏耀烜，彭志明

(长安大学建筑工程学院，陕西西安 710061)

0 引 言

目前，灾害脆弱性已经成为制约城市可持续发展的关键问题[1-4]。美国北岭地震和日本阪神地震后，为避免节点发生脆性破坏，从而提高钢框架整体抗震性能，各国学者提出了改进钢框架梁-柱延性节点的措施，主要集中在削弱型或加强型、端板连接型和带悬臂短梁的拼接型节点[5-8]，此类节点虽能改善梁端焊缝处的受力状况，但功能较为单一，未考虑受损后的快速修复性。

如何实现震后结构快速恢复功能成为工程抗震领域的一个研究趋势[9-12]。可更换梁柱节点在抗震设计时引入损伤控制理念，采用可拆卸更换的损伤元件，使震时塑性变形主要集中于损伤元[13]，其余构件保持弹性，震后仅需更换受损部件即可恢复结构使用功能。

本文基于保险丝和塑性铰外移理念，将外伸端板连接、削弱型和拼接型连接的优点进行整合，提出一种局部可更换钢框架梁-柱连接节点(以下简称新型节点)，如图1所示。该节点能够实现“塑性铰外移+耗能+可更换”三重功能的叠加，将其应用于地震区的钢框架中，能够在保证安全的基础上，快速恢复结构的使用功能。选取端板连接和拼接节点2个典型试验进行模拟，验证有限元建模过程的可靠性，然后对试件进行参数分析，研究短梁翼缘削弱深度c、削弱长度b及短梁长度l对节点承载力、耗能能力及延性的影响。

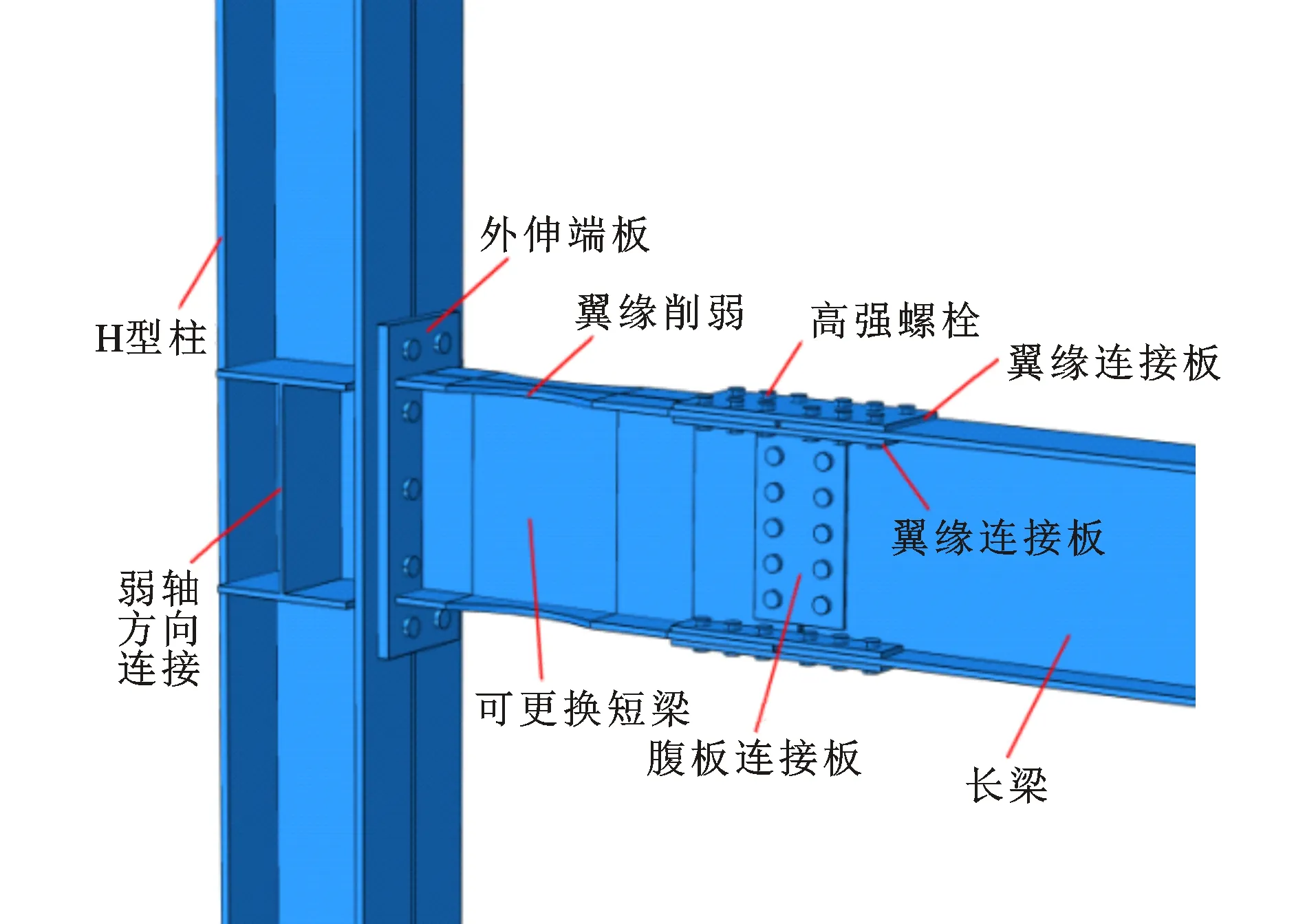
图1 局部可更换钢框架梁-柱节点

1 有限元建模及加载制度

1.1 BASE试件有限元模型建立

参照文献[14]，BASE试件梁长取2.4 m，柱高2 m。柱截面尺寸为HW350×350×12×19，梁截面尺寸为HN450×200×9×14，节点详细尺寸如图2所示。端板尺寸为-670 mm×250 mm×26 mm；梁翼缘拼接外侧连接板尺寸为-470 mm×200 mm×12 mm，内侧连接板尺寸为-470 mm×80 mm×12 mm；腹板拼接连接板尺寸为-370 mm×200 mm×8 mm；节点域焊接H型连接件为HM450×312×9×14，选用10.9级M20和M24两种高强度螺栓，拼接连接采用M20，端板连接采用M24，螺栓孔径分别取22 mm和26 mm。

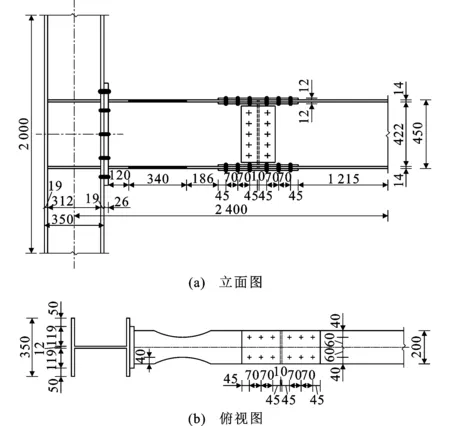
图2 节点详图(单位:mm)

1.2 材料属性

除高强度螺栓外，其余部件钢材均为Q235B，泊松比取0.3，参考文献[15]，[16]。

1.3 单元类型及网格划分

本文模型螺栓数目较多，为保证网格划分质量和精度，将螺栓孔单独切割出来，单元类型采用楔形；除螺栓孔外，其余均采用C3D8I单元类型。梁、柱、端板和拼接板采用结构化网格划分技术；螺栓采用扫掠网格划分技术和中性轴算法。柱节点域和端板连接处网格尺寸取12 mm×12 mm；短梁网格尺寸取24 mm×24 mm，翼缘削弱处和拼接处等部位进行加密处理，网格尺寸取12 mm×12 mm；柱和长梁的非关键区域网格尺寸取60 mm×60 mm；螺栓网格尺寸取6 mm×6 mm；网格划分如图3所示。

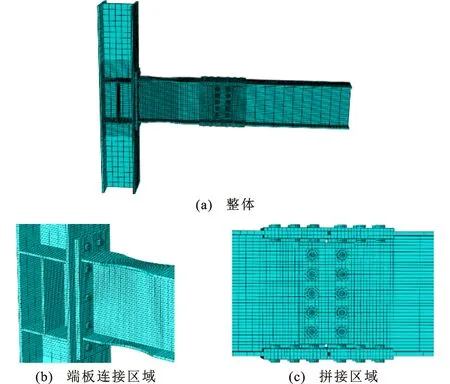
图3 网格划分

1.4 边界条件及加载方式

柱顶和柱底均视作铰接；轴压比取0.3，对柱顶面施加62 MPa的均布压力，约束柱顶X，Y方向的平动，允许其在轴压力作用产生Z方向位移；对柱底约束X，Y，Z三个方向的平动。为防止出现平面外失稳，约束梁X方向的平动。本文采用梁端位移加载方式，具体加载制度见表1。为满足FEMA-267[17]对层间位移角θ的要求，以保证钢框架的耗能能力，设定最大循环位移加载幅值为120 mm，即θ=0.05 rad。

2 有限元建模验证

2.1 外伸端板型节点的有限元验证

2.1.1 试验基本概况

本节选取文献[15]中JD3试件为验证对象，试验装置如图4所示。

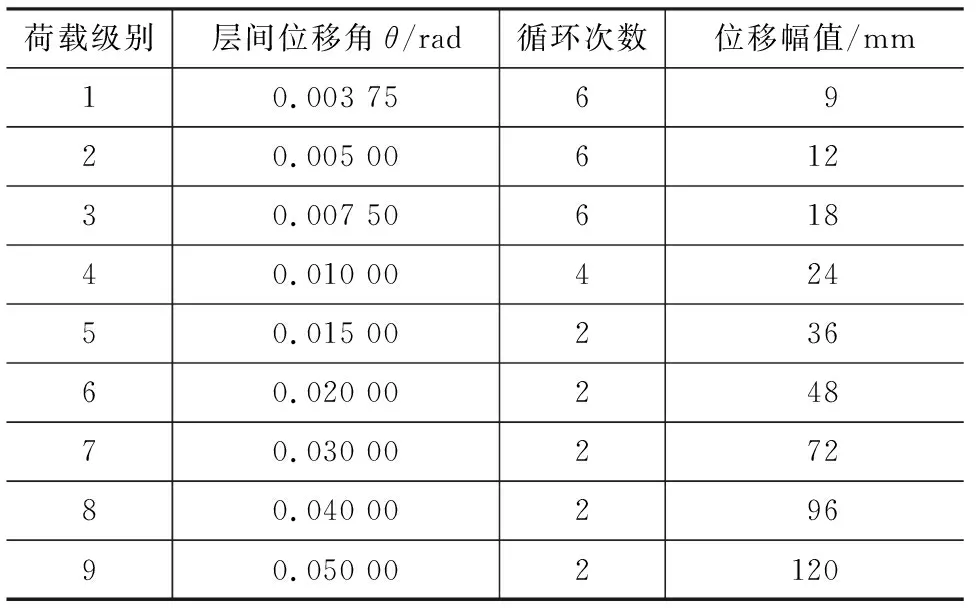
表1 加载制度Tab.1 Loading System

图4 试验装置1

试验采用梁端加载，试件屈服前采用荷载增量控制，分为3级，每级循环1次；节点屈服后采用位移增量控制，增量为10 mm，每级循环2次，直至试件破坏。为方便模拟，有限元分析时整个加载过程均采用位移控制。图5为按照前述建模方法得到的有限元模型，柱的两端视为铰接，轴压比取0.17，轴向压力为485 kN。

图5 有限元模型1

图6 破坏形态1

2.1.2 有限元计算结果与试验结果对比

试验和有限元模拟的最终破坏形态如图6所示。由图6可以看出，两者变形基本一致。试验表现为端板受拉区与柱翼缘之间存在较大间隙，节点域有较为明显的剪切变形，柱腹板表面涂漆出现脱落，最终破坏为受拉翼缘内侧1个螺栓被拉断，受压翼缘外侧的2个螺栓颈缩松动。有限元计算结果表明，外伸端板出现较大屈曲，受拉翼缘两侧的螺栓达到其极限承载力，节点域的柱腹板也出现一定塑性变形。

试验和有限元模拟得到的滞回曲线如图7所示，滞回曲线不是很饱满，这是由于在循环荷载作用下产生塑性应变积累，导致端板、柱翼缘和螺栓之间的接触间隙不断增大变化，有限元计算出现收敛问题，此时螺栓应力达到极限承载力。整体而言，2条曲线变化趋势一致，峰值点相差不大。

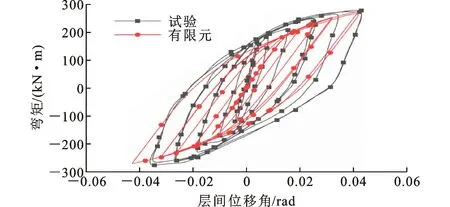
图7 滞回曲线对比1

试件的极限荷载和极限转角计算结果见表2。可以看出，有限元模拟得到的结果小于试验值，两者相差较小，相对误差在4.6%以内，极限转角相对误差为9.3%。

表2 试验结果与有限元计算结果对比1Tab.2 Comparison of Test Results and Finite Element Calculation Results 1

2.2 拼接型节点的有限元验证

2.2.1 试验基本概况

为验证梁拼接部分建模方法的准确性，选取文献[16]中CT-RBS试件进行模拟。

试验装置如图8所示，将柱两端固定于地面，对长梁进行侧向约束，阻止某平面外失稳。图9为划分好网格的有限元模型，单元总数为41 164个。加载制度采用美国钢结构抗震规范ANSI/AISC 341-10[18]第6.2节中定义的加载方式，梁端位移为0.375%θ，0.5%θ，0.75%θ时，每级循环6次；1.0%θ时，循环4次；1.5%θ，2%θ，3%θ，4%θ和5%θ时，每级循环2次，如图10所示。

图8 试验装置2

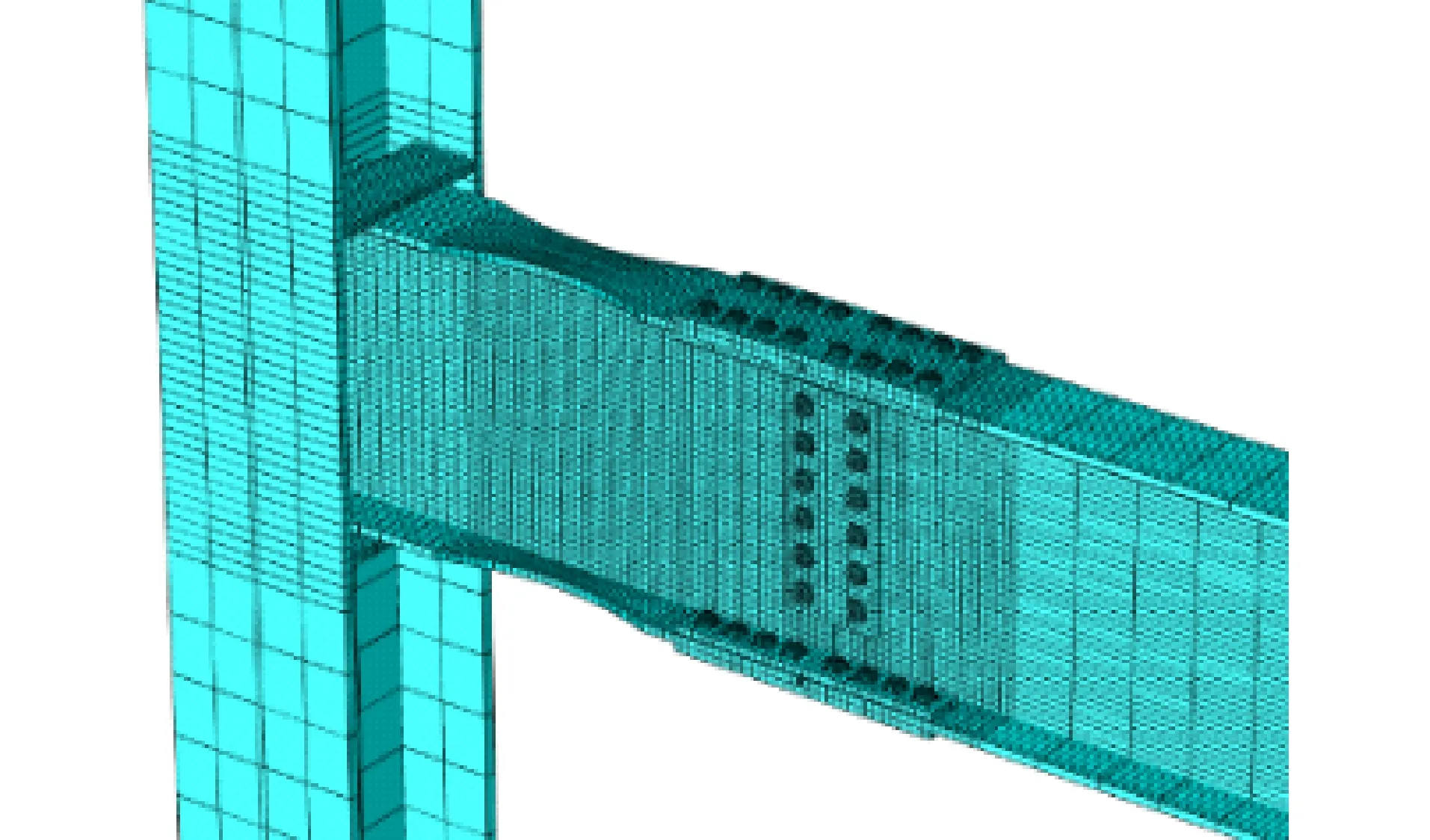
图9 有限元模型2

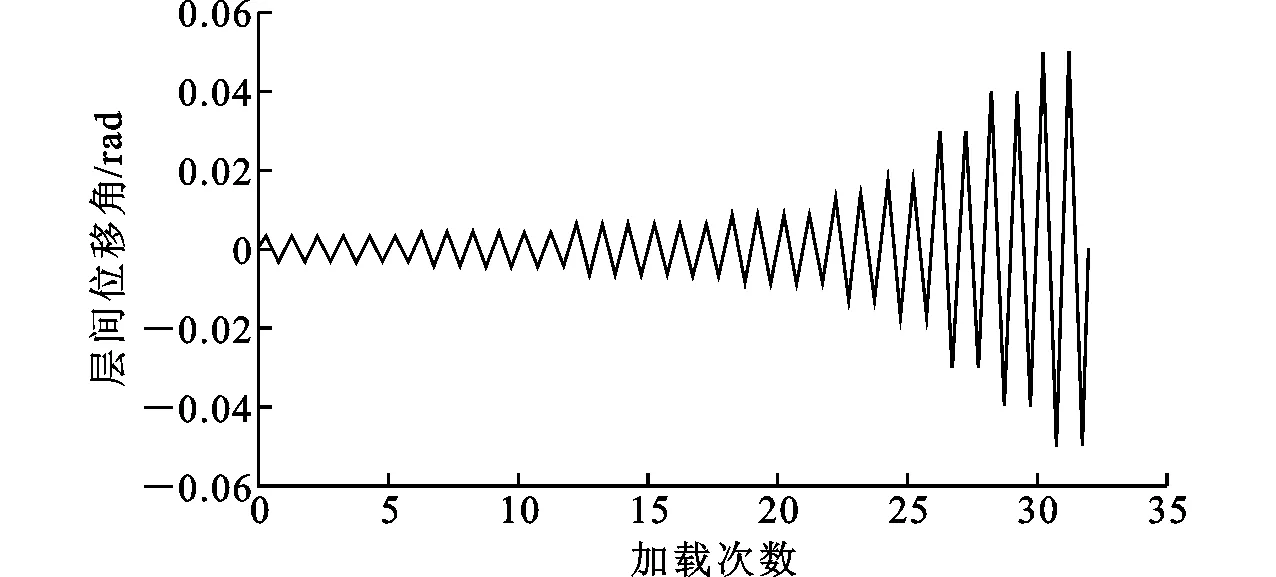
图10 加载制度

2.2.2 有限元计算结果与试验结果对比

试验和有限元模拟得到的滞回曲线如图11所示，其中M为节点弯矩，Mp为梁截面塑性弯矩。在弹性阶段，两者曲线基本重合；在弹塑性阶段，有限元较好地模拟出了试件的强化现象，说明本文有限元建模时材料属性及边界条件设置合理。有限元的滞回曲线相对更加饱满，这是由于建模时未考虑钢材损伤及焊缝的影响，模拟条件较为理想。整体而言，2条曲线变化趋势一致，峰值点相差也不大，吻合较好。

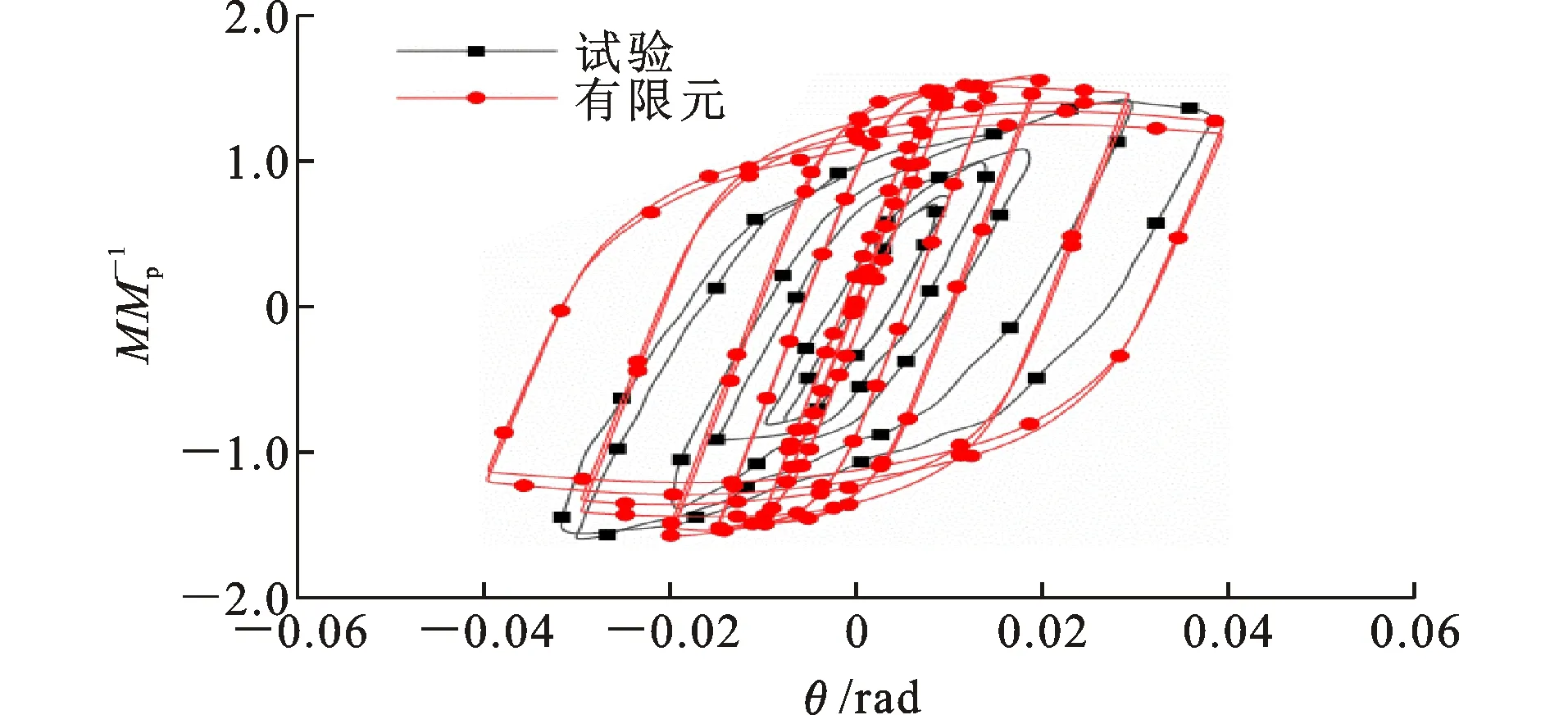
图11 滞回曲线对比2

试验和有限元模拟的破坏形态对比如图12所示。试验表现为：层间位移角为0.01 rad时，梁翼缘开始屈服，随着荷载的增大，梁腹板及加劲肋逐渐屈服，当层间位移角达0.05 rad时，短梁削弱区域发生屈曲破坏。有限元计算结果表明：加载初期，加劲肋及柱腹板区域处应力较大，随着层间位移角的增大，应力发生重分布；当加载至0.05 rad时，最大应力出现在梁翼缘削弱区域，翼缘和腹板出现不同程度的屈曲；最终破坏形态与试验现象基本一致。

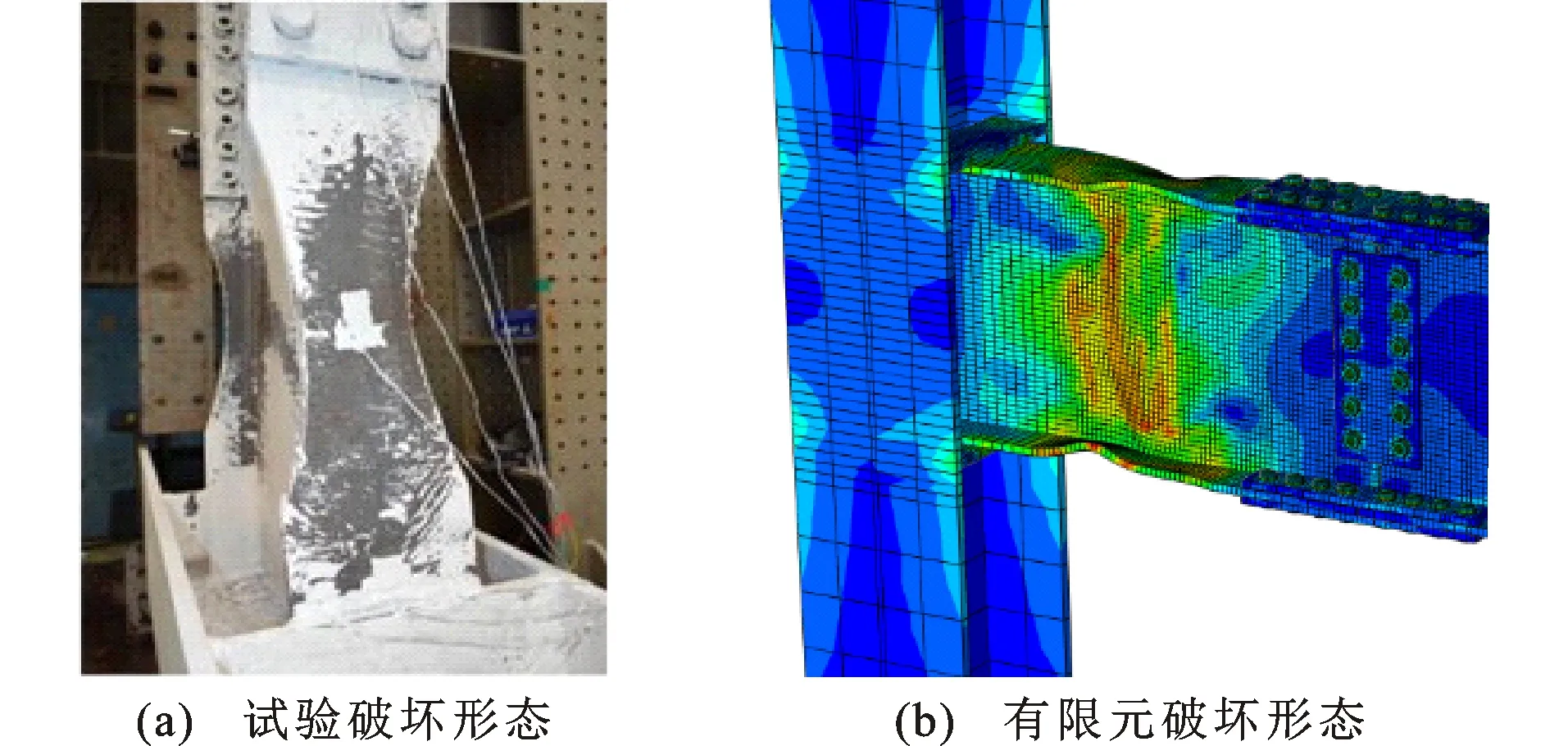
图12 破坏形态2

试验和有限元计算得到的承载力如表3所示。可以看出，有限元模拟得到的结果略大于试验值，两者的屈服荷载相差6.8%，极限荷载相差约为8.1%。这是由于建模时未考虑钢材损伤、焊接缺陷及安装误差等因素的影响。有限元与试验相对误差小于10%，在可接受范围内，说明有限元建模方法较为准确，可以用于后续研究。

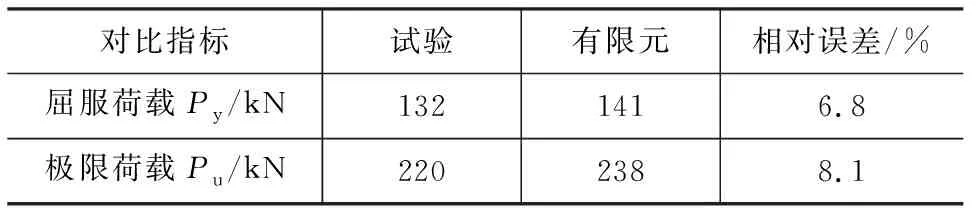
表3 试验结果与有限元计算结果对比2Tab.3 Comparison of Test Results and Finite Element Calculation Results 2

3 变参数分析

3.1 翼缘削弱深度c的影响

为研究梁翼缘削弱深度c对新型节点在循环荷载作用下力学性能的影响，设计了RD系列试件，如表4所示，其余参数和BASE试件保持一致。

表4 RD系列试件设计参数Tab.4 Design Parameters of RD Series Specimens

3.1.1 破坏形态

图13，14为RD系列试件在层间位移角为0.05 rad时的应力云图及PEEQ应变云图。与BASE试件相比，RD-1，RD-2试件由于未进行削弱或削弱不足，塑性铰外移不明显，最大应力和塑性应变出现在梁翼缘与端板焊缝处及节点域柱腹板位置，震后节点域受到损坏，难以实现可更换修复这一目的。由RD-3～RD-5，BASE试件的云图可知，短梁削弱处翼缘及腹板发生不同程度的局部屈曲，塑性变形随着削弱深度的增大而增加，且逐渐远离梁端。

3.1.2 滞回曲线与骨架曲线

弯矩-转角曲线能直观反映出节点在受力过程中的变形特征及极限状态，故常用该曲线来研究节点的滞回性能。节点弯矩M=Pl′，其中P为梁端荷载，l′为加载点至柱面的距离。层间位移角θ=Δ/l0，反映梁柱节点整体弹性变形和塑性变形，其中Δ为加载点的竖向位移，l0为加载点至柱截面中心的距离。

RD系列试件的M-θ滞回曲线如图15所示，其中θp为节点的塑性转角。可以看出，试件RD-2～RD-5及试件BASE的滞回曲线均较饱满，未出现捏缩现象，说明按等强设计法确定的螺栓数目使得拼接板螺栓的静摩擦力不易被克服，在整个加载过程中并没有发生滑移。试件RD-1由于未进行削弱，当反向加载到0.03 rad时，上翼缘两侧的螺栓应力已超出其承载能力，导致有限元计算出现收敛问题。虽然RD-1的承载力很高，但其延性和耗能能力较差，层间位移角较小时即发生螺栓断裂破坏，试件的抗震性能未能得到充分发挥，故下文对比分析时，不再考虑试件RD-1。

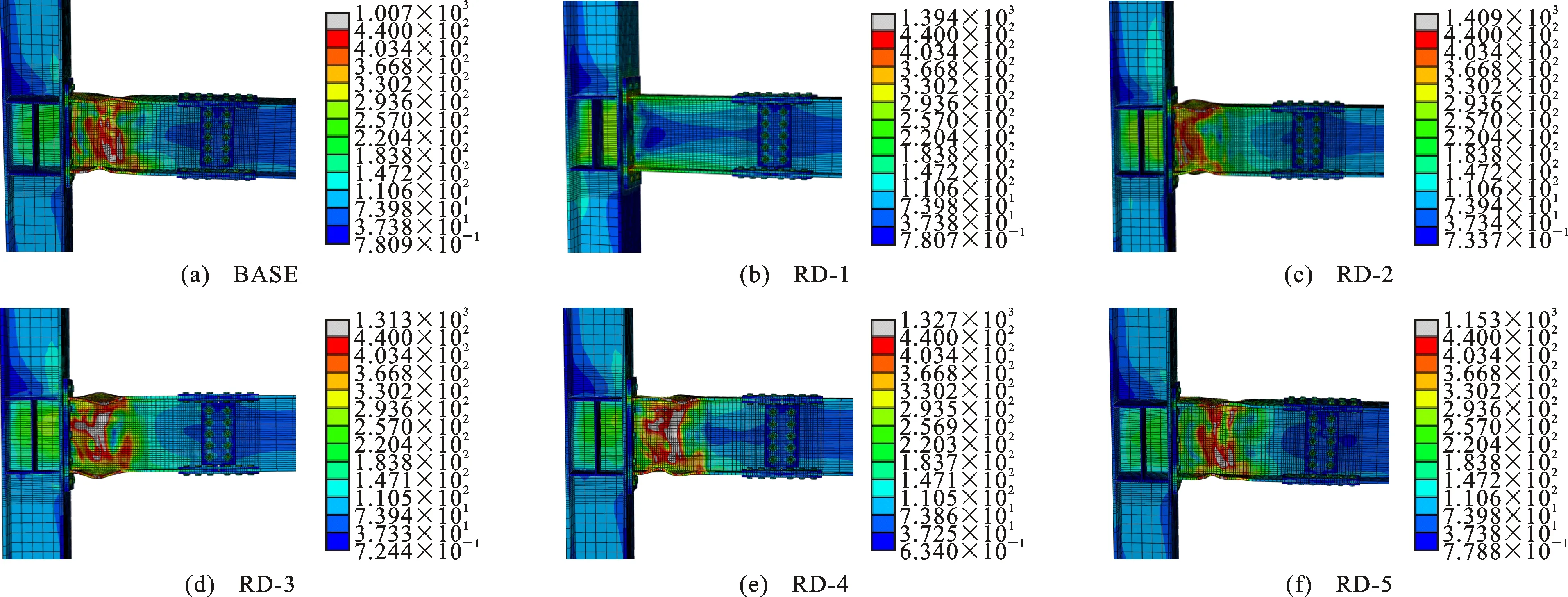
图13 RD系列试件的Mises应力云图(单位:MPa)

图14 RD系列试件的PEEQ应变云图

ANSI/AISC314-10[18]规定：在抗弯钢框架中，层间位移角在0.04 rad时节点承载力不应小于0.8Mp。本文各试件的梁截面尺寸一致，正负弯矩作用下0.8MP相同，均为0.8MP=305 kN·m。由图15可知，当层间位移角为0.04 rad时，试件RD-2～RD-4的弯矩大于0.8Mp，试件RD-5的弯矩小于0.8Mp，说明翼缘削弱深度不应过大，否则将不满足抗震要求。

弯矩-塑性转角曲线反映了节点的塑性转动能力，采用简化计算方法[19]确定塑性转角θp(图16)，公式如下

(1)

(2)

式中：Δ0为梁端塑性铰处竖向位移；Δe为由弹性变形引起的梁端位移；L0为加载点至柱截面中心的距离；EI为抗弯刚度。

FEMA-267规定：梁柱节点的塑性转角不应小于0.03 rad。比较图15可知，M-θp滞回曲线更加饱满，RD系列试件最大塑性转角大于0.04 rad，塑性变形占总变形的80%以上，可见新型节点具有良好的塑性转动能力。

RD系列试件的骨架曲线如图17所示。可以看出，各曲线均经历了明显的弹性上升阶段、弹塑性阶段和破坏阶段。当层间位移角小于屈服转角时，各试件骨架曲线基本重合，呈线性增长。当层间位移角大于0.01 rad后，试件进入弹塑性阶段，各骨架曲线开始出现差异。试件削弱深度越深，节点的极限承载力越小，加载结束时承载力下降的幅度越大。

图15 RD系列试件的滞回曲线

图16 塑性转角

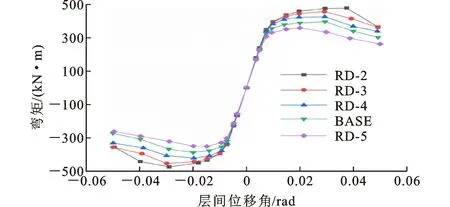
图17 RD系列试件的骨架曲线

3.1.3 承载力与延性

本文采用通用屈服弯矩法确定各试件的屈服弯矩My及屈服转角θy；弹性刚度Ek为节点屈服弯矩与屈服转角之比，即Ek=My/θy；极限转角θu为M-θ骨架曲线上节点荷载下降至85%峰值荷载时的转角。

延性反映了试件在非弹性变形阶段的变形能力，也是评价节点抗震性能的重要指标。节点延性的大小通过延性系数μ(μ=θu/θy)表示，μ值越大，试件的延性越好，承受塑性变形的能力越强。关于钢框架位移延性系数的规定，一般认为μ≥3即满足延性要求。

RD系列试件的力学性能指标见表5。可以看出，随着翼缘削弱深度c的增大，节点的屈服弯矩和最大弯矩有明显降低，弹性刚度表现为先增后减，延性系数呈增大趋势。RD-5的弹性刚度和延性系数小于BASE试件，这是由于当削弱深度超过一定值后，将导致屈服弯矩和极限转角大幅降低。RD系列试件最大承载力相差33.2%，延性系数最大相差10.4%，初始刚度最大相差8%，说明c值的变化对节点承载力和延性影响较大。与试件RD-2和RD-5相比，RD-3，RD-4，BASE试件的各项力学指标良好，在保证承载力的同时也满足延性要求，表明削弱深度取值较合理，建议c取(0.1～0.2)bf，bf为钢梁截面宽度。

表5 RD系列试件的力学性能指标Tab.5 Mechanical Properties of RD Series Specimens

3.1.4 耗散能量分析

本文采用能量耗散系数E来衡量试件的耗能能力，滞回曲线的包络面积越大，E值就越大，节点的耗能能力越强[20]。

图18为RD系列试件的能量耗散系数曲线。当层间位移角小于0.04 rad时，能量耗散系数随着削弱深度c的增大而增大。这是由于c值越大，节点塑性发展的速度越快，试件耗能能力就越强。当层间位移角大于0.04 rad时，各节点的能量耗散系数相差逐渐减小；当层间位移角为0.05 rad时，各试件耗能系数近似相等。这是由于在加载后期，削弱深度过大的节点承载力下降过多，使得耗散的能量有所减少。

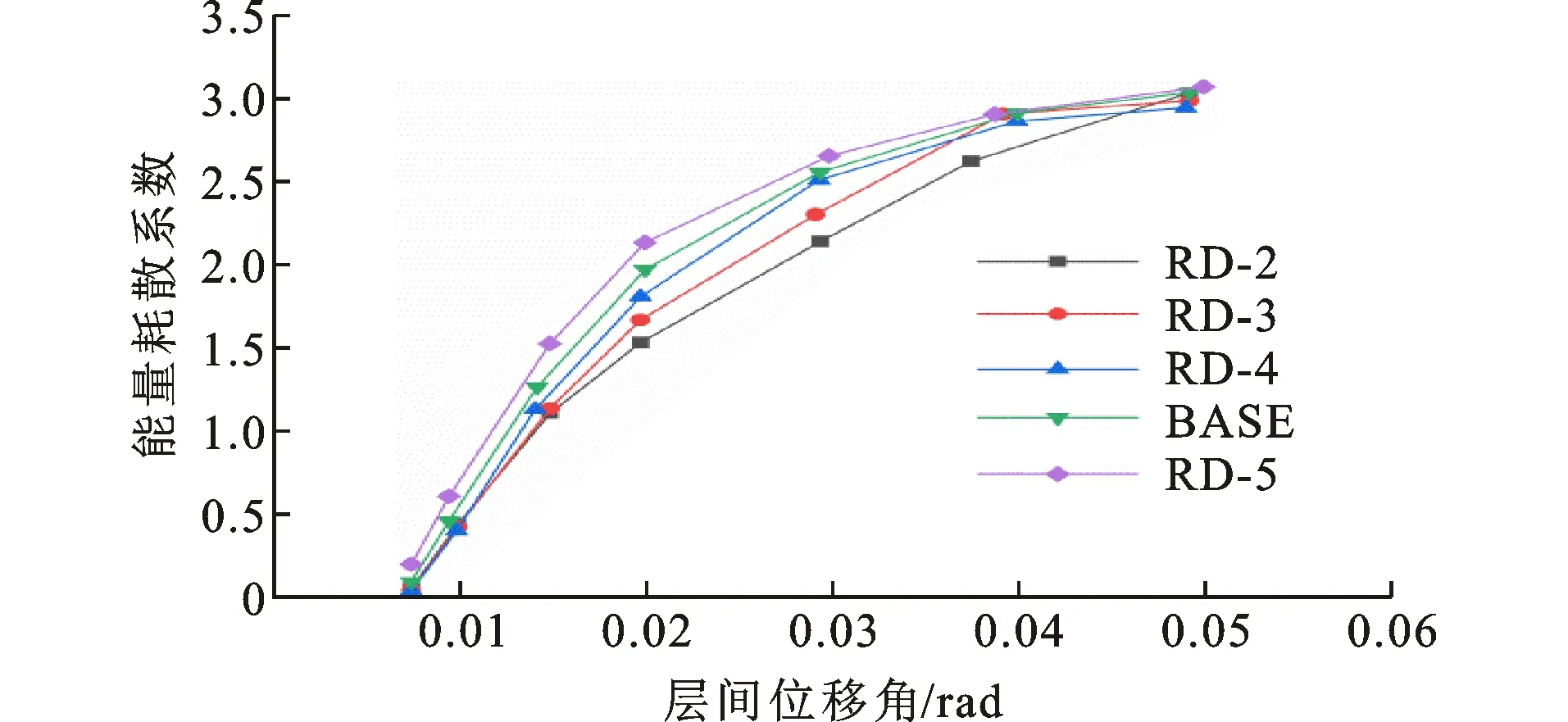
图18 RD系列试件的能量耗散系数曲线

3.2 翼缘削弱长度b的影响

为深入研究b对新型节点在循环荷载作用下力学性能的影响，设计了RL系列试件，见表6，其余参数和BASE试件保持一致。

表6 RL系列试件设计参数Tab.6 Design Parameters of RL Series Specimens

3.2.1 破坏形态

图19，20为RL系列试件在层间位移角为0.05 rad时的Mises应力云图及PEEQ应变云图。由于RL-1试件的b值较小，当试件发生破坏时，塑性变形发展不够充分，导致梁根部焊缝处存在较大的应力。由Mises应力云图可以看出，随着削弱长度b的增加，应力较大值逐渐远离梁端并向削弱区汇聚。由PEEQ应变云图可以看出，随着削弱长度的增加，塑性变形范围逐渐增大，而PEEQ值逐渐减小。由此可知，为使塑性铰外移顺畅，削弱长度b不宜太小，在规范取值范围内应尽可能取大值。

3.2.2 滞回曲线与骨架曲线

RL系列试件的滞回曲线如图21所示。随着削弱长度b的增加，各试件的滞回曲线变化不明显，均呈饱满的梭形状态。由图21(e)可知，当层间位移角为0.04 rad，试件RL-3，RL-4的弯矩小于0.8MP，不满足ANSI/AISC 314-10的相关规定，因此b值不应过大。由图21(f)可知，RL系列试件最大塑性转角大于0.04 rad，塑性变形占总变形的80%以上，均表现出较好的耗能能力。

RL系列试件的骨架曲线如图22所示。可以看出，从加载至强化阶段，各试件骨架曲线基本重合，试件的最大弯矩随削弱长度b值的增加而降低。当层间位移角大于0.03 rad时，各曲线开始呈下降趋势，削弱长度b值越大，承载力下降越明显。

3.2.3 承载力与延性

RL系列试件的力学性能指标见表7。由表7可知，弹性刚度相差3.8%，最大弯矩相差3.6%，随着削弱长度b的增加，节点的最大承载力有递减趋势，延性系数逐渐增大，RL-1与RL-3相差5.7%。综合考虑各项力学指标，b值取(0.65～0.85)hb，hb为钢梁截面高度。

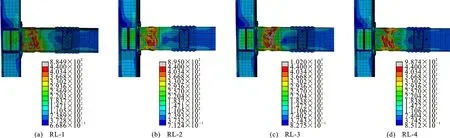
图19 RL系列试件的Mises应力云图(单位:MPa)

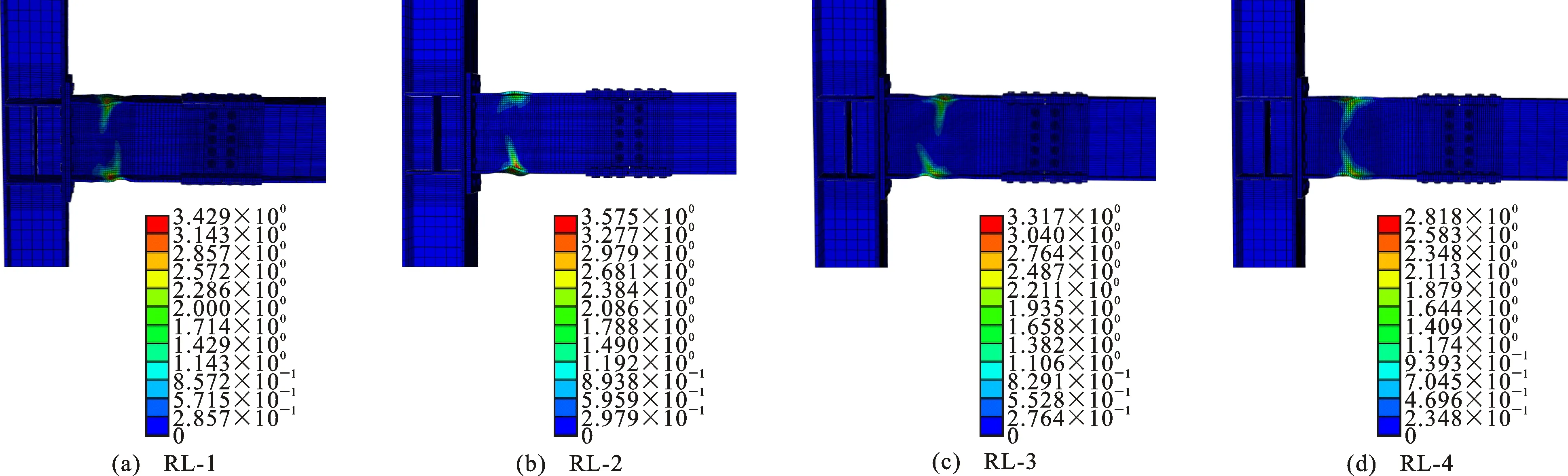
图20 RL系列试件的PEEQ应变云图

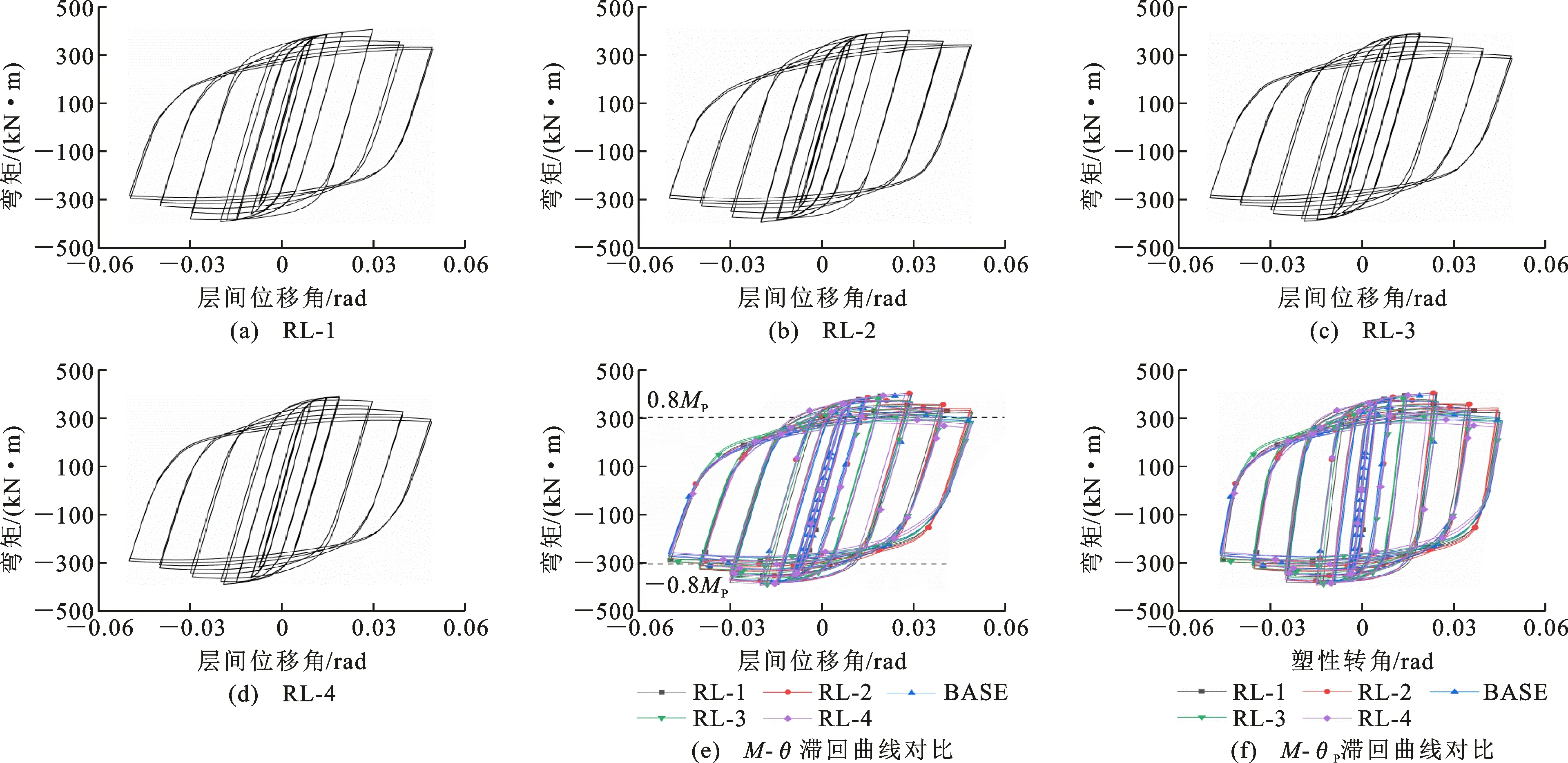
图21 RL系列试件的滞回曲线

3.2.4 耗散能量分析

RL系列试件的能量耗散系数曲线如图23所示。加载初期，由于试件尚处于弹性变形阶段，耗散

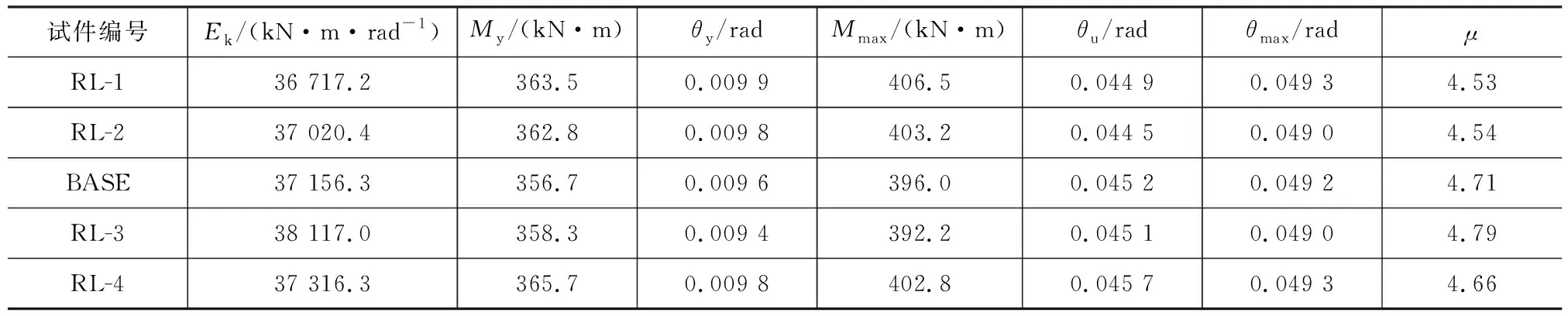
表7 RL系列试件的力学性能指标Tab.7 Mechanical Properties of RL Series Specimens

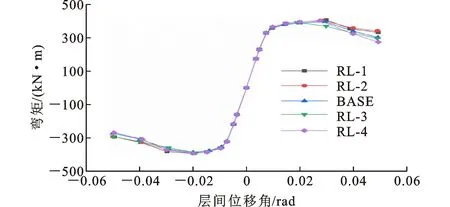
图22 RL系列试件的骨架曲线

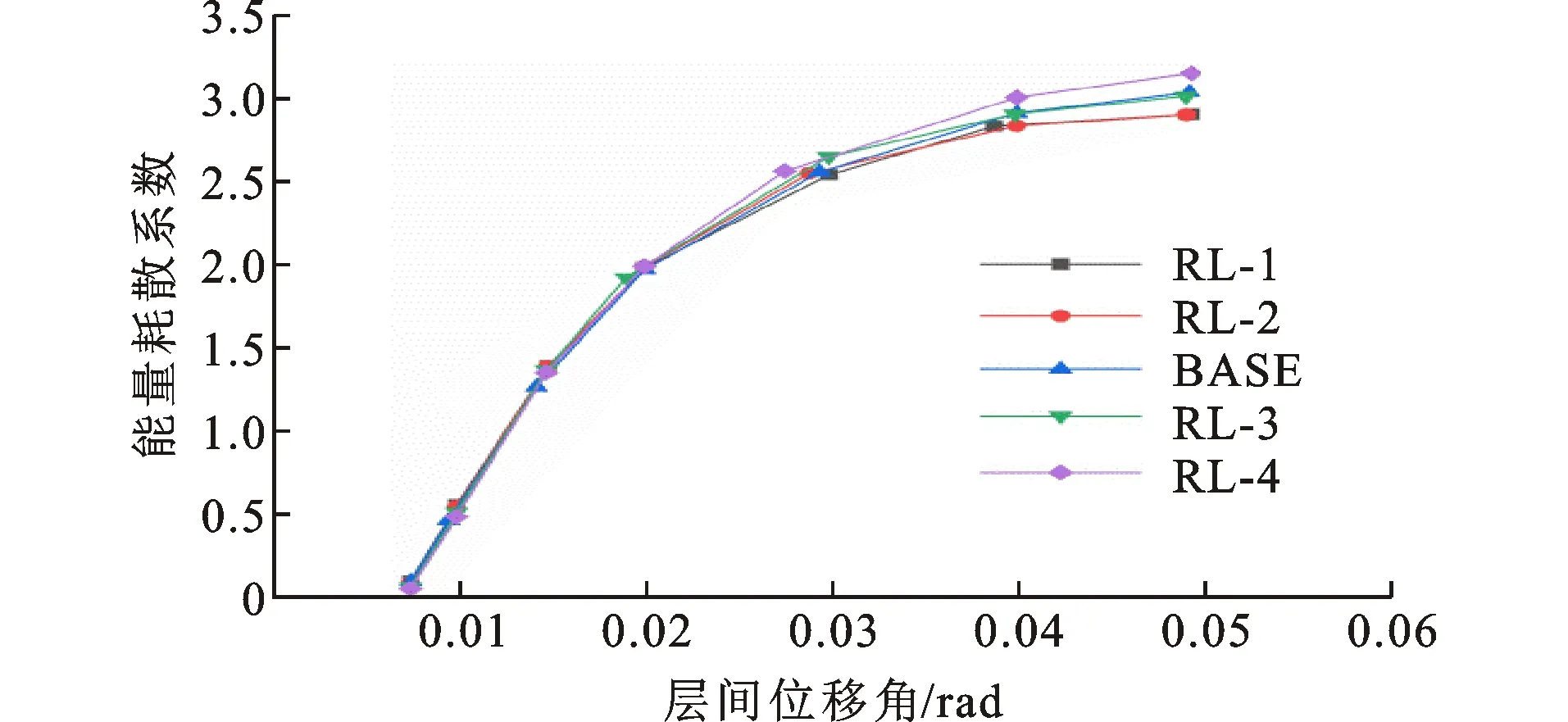
图23 RL系列试件的能量耗散系数曲线

的能量相对较小，各曲线基本重合，能量耗散系数较小。当层间位移角大于0.02 rad后，试件进入塑性发展阶段，各试件耗能能力表现出一定差异，能量耗散系数随着削弱长度b值的增加而增大。

3.3短梁长度l的影响

为研究短梁长度l对新型节点力学性能的影响，确定其合理取值，设计了BL系列试件，见表8，其余参数和BASE试件保持一致。

表8 BL系列试件设计参数Tab.8 Design Parameters of BL Series Specimens

3.3.1 破坏形态

图24,25为BL系列试件在层间位移角为0.05 rad时的Mises应力云图及PEEQ云图。可以看出，各试件的破坏形态基本一致，最大应力和塑性变形主要集中于短梁削弱区域，且其幅值相差不大。因此，在设计新型节点时，短梁长度只需满足端板连接、翼缘削弱尺寸及拼接连接构造要求即可。

3.3.2 滞回曲线与骨架曲线分析

BL系列试件的滞回曲线如图26所示。可以看出，各试件的M-θ曲线均呈饱满的梭形，正负向呈现较好的对称性，滞回环面积较大，表现出良好的耗能能力和抗震性能。在初始加载阶段，层间位移角较小，试件处于线弹性受力阶段，卸载后变形恢复。随着层间位移角的增大，弯矩与转角不再保持线性关系，卸载后出现一定的残余变形，试件处于弹塑性受力阶段。待荷载达到最大值后，试件的承载力开始出现下降，且下降幅度随着循环次数的增加而增大。由图26(e)可知，各试件的M-θ曲线基本重合，当层间位移角为0.04 rad时，各试件的弯矩均大于0.8MP，满足抗震要求。由图26(f)知，BL系列试件最大塑性转角大于0.04 rad，塑性变形占总变形的80%以上，表现出较好的耗能能力。

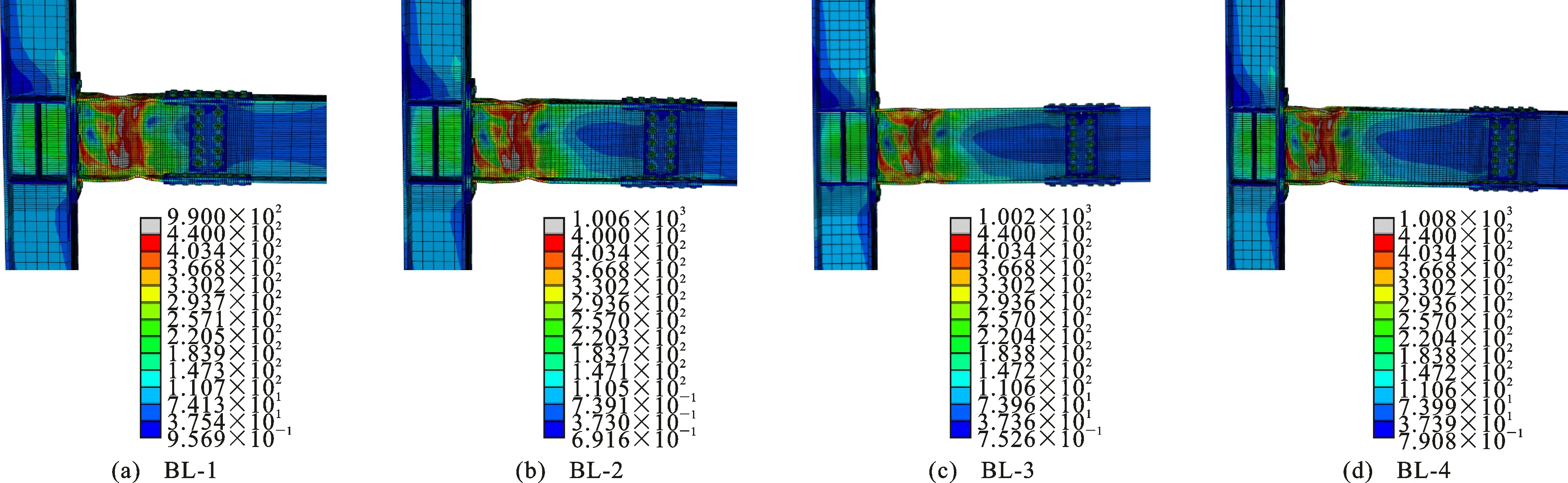
图24 BL系列试件的Mises应力云图(单位:MPa)

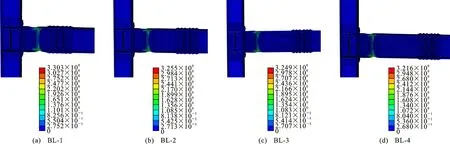
图25 BL系列试件的PEEQ应变云图

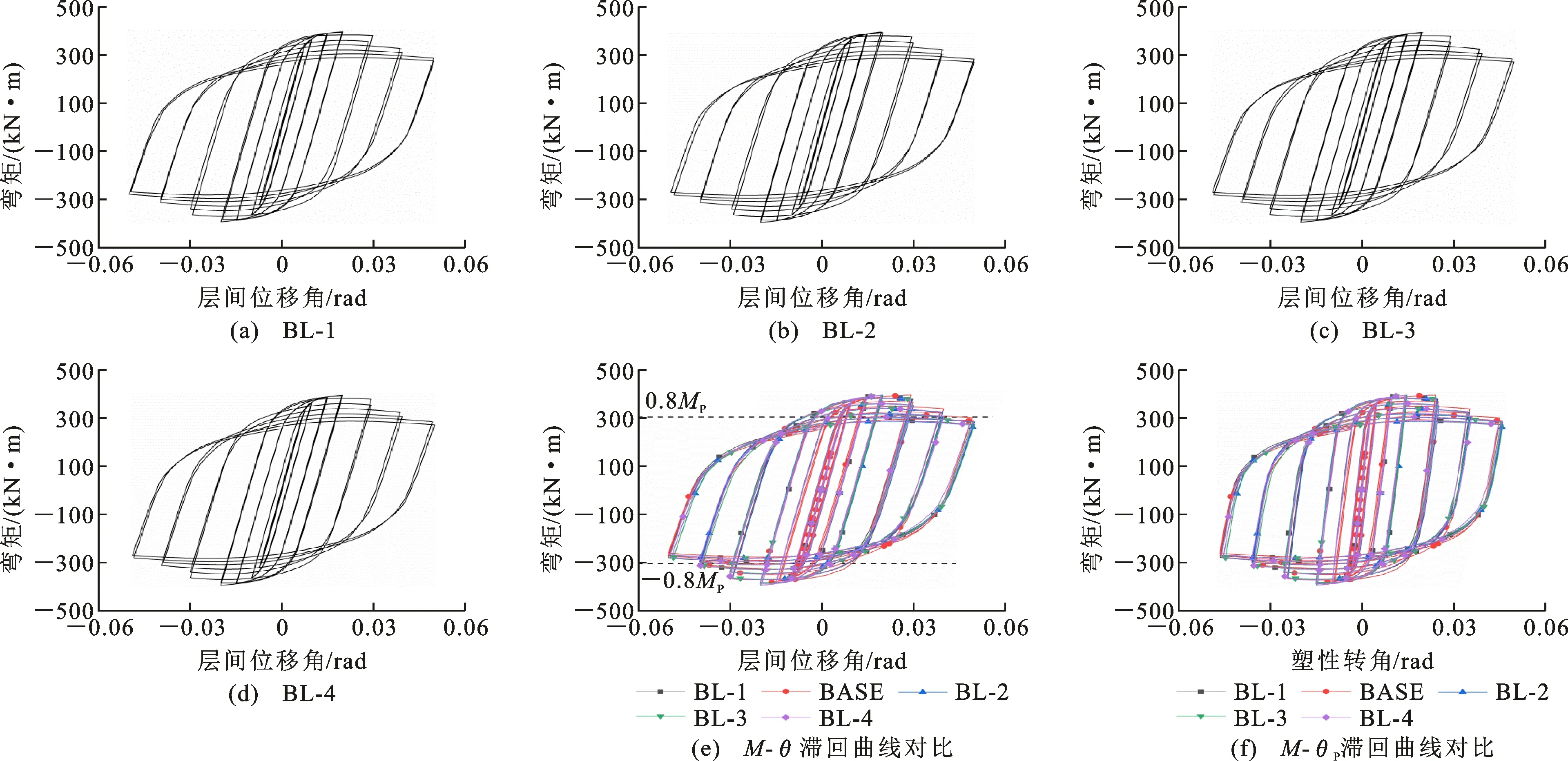
图26 BL系列试件的滞回曲线

BL系列试件的骨架曲线如图27所示。可以看出，各曲线均经历了明显的弹性上升阶段、弹塑性阶段和破坏阶段。在整个加载过程中，各骨架曲线基本重合，说明短梁长度l的变化对节点的承载能力和变形能力影响较小。

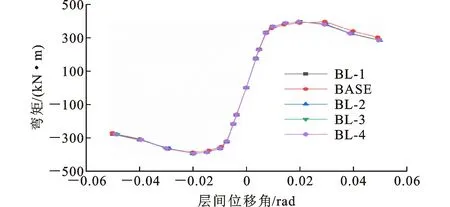
图27 BL系列试件的骨架曲线

3.3.3 承载力与延性分析

BL系列试件的力学性能指标见表9。由表9可知，试件BL-1，BL-4的最大承载力相差仅0.2%，说明短梁长度l对节点承载力影响不大。除BASE试件外，节点的延性系数随着短梁长度l的增加呈递减趋势。BASE试件的延性系数大于4，这是由于短梁的削弱尺寸与BASE试件的短梁长度l匹配较好。鉴于短梁长度l对节点各项力学指标的影响较小，考虑到经济性及运输方便性，建议l取(1.5～2.5)hb。

表9 BL系列试件的力学性能指标Tab.9 Mechanical Properties of BL Series Specimens

3.3.4 耗散能量分析

BL系列试件的能量耗散系数曲线如图28所示。由图28可知，在整个加载过程中，各曲线基本重合，能量耗散系数随层间位移角的增大而增大。当层间位移角较小时，试件处于弹性受力阶段，弯矩与转角呈线性关系，卸载后曲线沿原路径返回，无残余变形，能量耗散系数较小。随着梁端荷载的增加，当试件进入塑性阶段后，能量耗散系数开始逐渐增加。同一层间位移角下，各试件的能量耗散系数近似相等，说明短梁长度的变化对节点耗能能力影响不大。

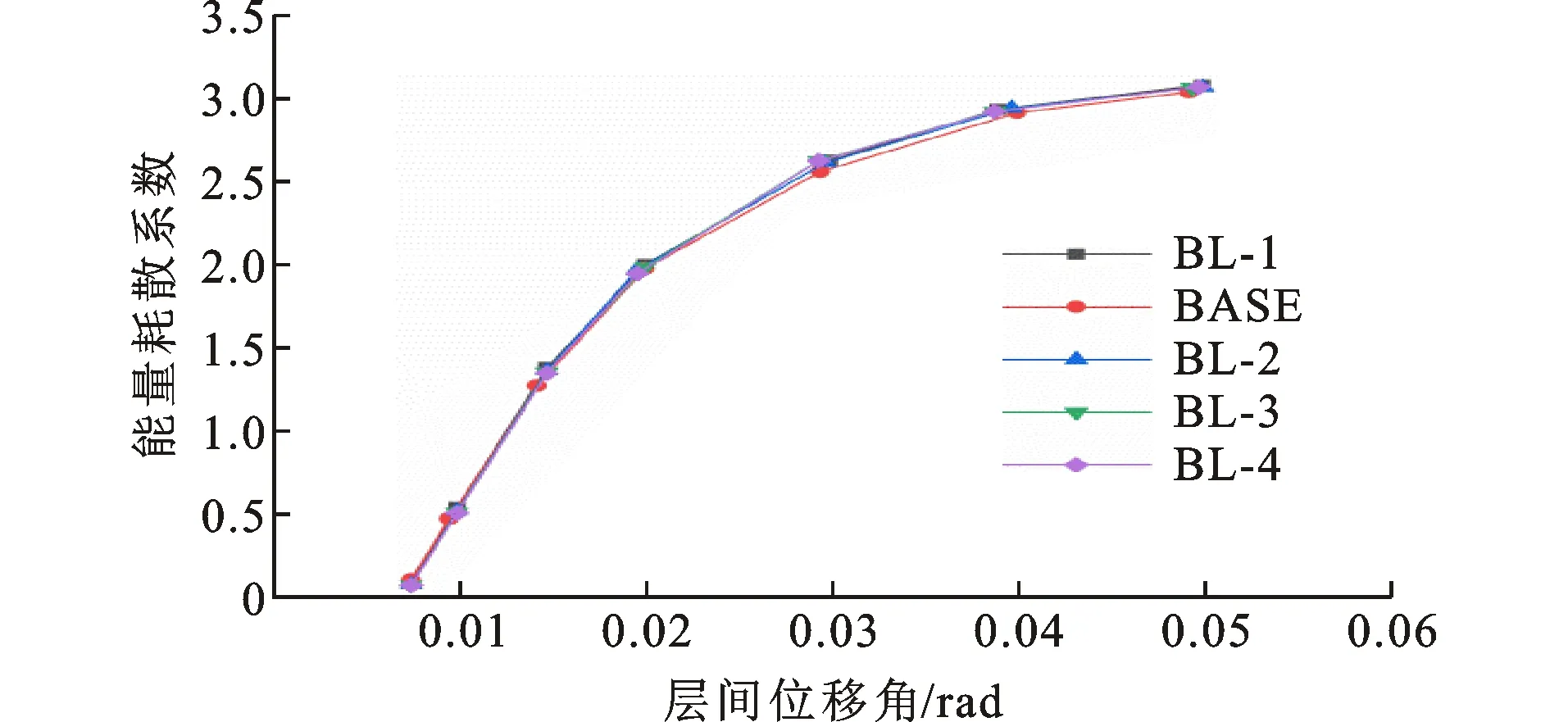
图28 BL系列试件的能量耗散系数曲线

4 结语

(1)基于数值模拟，对新型节点的力学性能进行研究。选取端板连接和拼接节点2个典型试验进行模拟，验证有限元建模过程的可靠性。

(2)研究了短梁翼缘削弱深度c、削弱长度b对节点承载力、耗能能力及延性的影响；参数对节点的力学性能影响程度由大到小依次为c，b，l,随着c值的增大，节点的承载力有明显降低，而耗能能力和延性有所提高。随着b值的增大，节点的最大承载力有所减小，而延性系数随之增大。短梁长度l对节点力学性能的影响基本可忽略不计。

(3)综合考虑节点的各项力学性能及经济性，建议c取(0.1～0.2)bf，b取(0.65～0.85)hb，建议l取(1.5～2.5)hb。