内置高强角钢的方钢管混凝土柱偏压性能试验
2021-04-06刘晓珠
吴 波,王 辉,刘晓珠
(华南理工大学亚热带建筑科学国家重点实验室,广东广州 510640)
0 引 言
钢管混凝土柱承载力高,延性好,施工简便[1],国内外学者对其开展了大量研究[2-7],已广泛应用于高层建筑和大跨桥梁[8],并形成了一系列设计标准[9-12]。钢管外露导致该类柱的耐火性能通常较差,为此前人提出了各种增强措施(如在钢管内部设置双钢管[13]、纵向加劲肋[14]、工字型钢[15]、钢筋笼[16]等),以求有效提升钢管混凝土柱的耐火性能。然而这些措施几乎都是在已有钢管基础上额外增加钢材用量,不但造价增加,其中一些措施还会造成梁-柱节点区的复杂程度与施工难度加大。为解决此问题,文献[17]中提出了内置高强角钢的方钢管混凝土柱,即在总用钢量保持不变的前提下,将钢管壁适当减薄并在管内设置Q690高强角钢,且钢管与角钢之间预留一定净距。对该类柱开展的明火试验和轴压试验表明,总用钢量基本相同时,内置高强角钢的方钢管混凝土柱比传统无内置角钢柱的耐火极限提升幅度超过200%,且轴压承载力与延性系数也有所提高。钢管减薄是否会对该类柱的偏压性能产生明显不利影响尚待进一步明确。若果真如此,必然会对该类柱的工程应用产生限制。
因此,本文开展了8根内置高强角钢的方钢管混凝土柱和2根传统方钢管混凝土柱的偏压试验,考察了主要参数对前者偏压性能的影响规律,提出了改进的偏压承载力实用计算方法。
1 试验概况
1.1 试件设计与材料特性
本试验共设计了10个试件,其中包括8根内置高强角钢的方钢管混凝土柱及2根传统方钢管混凝土柱,各试件的总用钢量基本相同。所有试件的高度均为1 120 mm,加上顶板、底板及加载时所用铰支座之后,上、下铰支点间的距离为1 440 mm。试件外边长为240 mm,高宽比为6,属于中长柱[18]。角钢肢长有25 mm和45 mm两种类型,肢厚和高度都只有一种类型,分别为5 mm和1 130 mm。为方便角钢上应变片引线的导出,所有内置角钢试件均需要在顶板上钻孔开槽,槽深度为10 mm。此外,为了使角钢顺利伸出进而与顶板牢固焊接,在顶板上角钢对应位置处设置通缝,缝宽度为10 mm,大于角钢厚度。图1为典型试件示意图。
试验参数包括:①钢管壁厚t为4,5,6 mm;②取钢率γ(角钢质量与钢管+角钢总质量之比)为16.3%,30.7%;③角钢到钢管内壁净距S为10,30 mm;④试件偏心距e为60,120 mm。
试件编号及具体参数见表1,其中T6-E60,T6-E120为传统方钢管混凝土柱,B和L分别为方钢管的外边长与高度,w和t1分别为角钢的肢长和肢厚。
钢管和角钢分别采用Q345和Q690钢材,其力学性能指标按照《金属材料拉伸试验第1部分:室温试验方法》[19]测取,具体见表2和图2。由于拉伸试样上粘贴的应变片的测量范围有限,图2只给出了Q690钢材的部分应力-应变曲线。名义壁厚为6,5,4 mm的方钢管,其实测壁厚分别为5.84,4.86,3.88 mm; 名义肢厚为5 mm的角钢,其实测肢厚为4.94 mm。
图3为试件的制备过程。首先在底板上划线来定位角钢和钢管,随后将4根角钢和钢管依次焊接于底板上。所有试件均采用立式浇筑,混凝土从顶部倒入,同时用振捣棒将其振捣密实。养护完成后,用高强石膏对所有试件上表面进行找平,并把角钢及钢管依次与顶板焊接,同时在试件上、下两端焊接三角形加劲肋,加劲肋的直角边为110 mm,厚度为8 mm。本文试验采用C30商品混凝土,其配合比如表3所示。
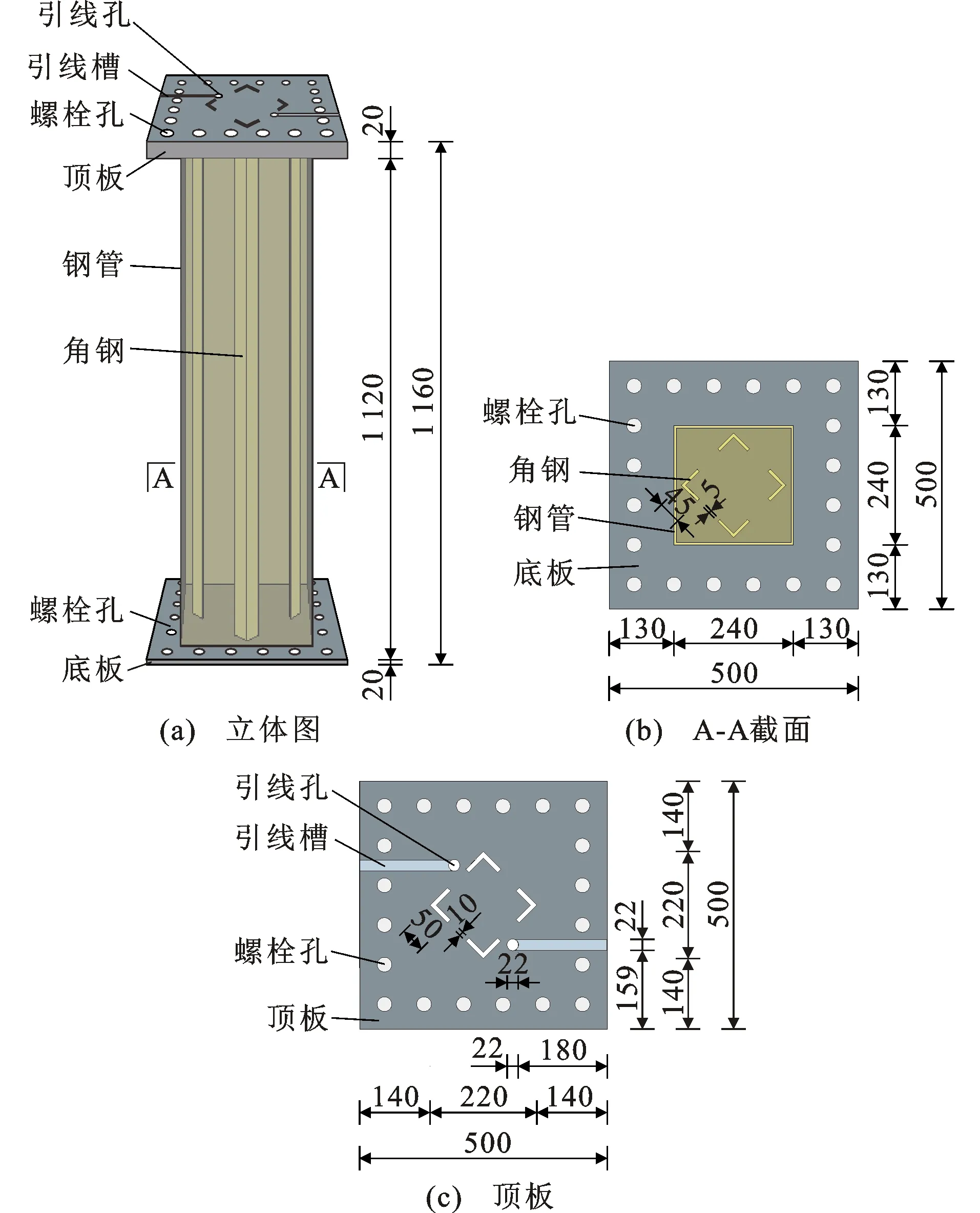
图1 试件T4-R31-S10-E60示意图(单位:mm)
试件浇筑时,用同批次商品混凝土浇筑一定数量边长为150 mm的立方体试块和φ150×300的圆柱体试块。试验前一天,依照GB/T 50081—2019规范[20]测得的混凝土立方体抗压强度fcu和混凝土轴心抗压强度fc分别为49.6 MPa和40.2 MPa,弹性模量为33.4 GPa。
1.2 测点布置与加载装置
图4所示为试件的变形和应变测量方案。试件竖向变形由上加载板处沿竖向设置的1个位移传感器来测取。按照相同方式在试件顶板处布置2个位移传感器,分别测取试件受拉侧、受压侧竖向变形,利用所测数据可推算出上铰支点的竖向变形,对比结果表明该处竖向变形和上加载板的竖向变形基本相同。另外,沿试件高度等间距水平设置了7个位移传感器,以测量试件的侧向挠度。
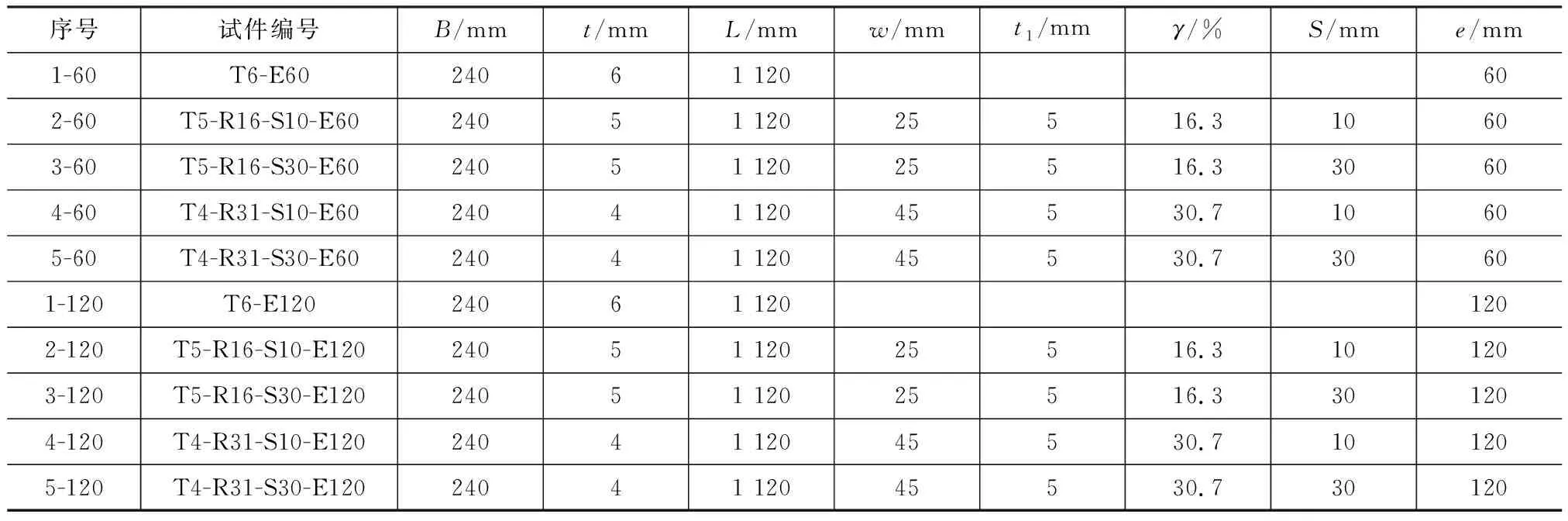
表1 试件具体参数Tab.1 Details of Specimens

表2 钢材力学性能Tab.2 Mechanical Properties of Steel
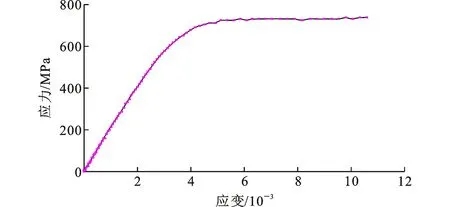
图2 Q690钢材的实测应力-应变曲线

图3 试件制备
在方钢管半高处的受压与受拉侧分别设有3对纵、横向应变片,另有5对纵、横向应变片在钢管半高处沿偏心方向一侧间隔60 mm布置。对每根高强角钢,在其半高处肢长中心点的外侧表面布置1对纵、横向应变片。
试验在华南理工大学结构实验室的1 500 t长柱压力机上进行,试件上、下两端通过铰支座与压力机相连。
本文试验中加载方式选用位移控制方式,峰值荷载前后加载速率分别设置为0.003 mm·s-1和0.005 mm·s-1。为防止试件侧向挠度过大而引发安全事故,当荷载下降至80%峰值荷载或试件竖向变形大于35 mm时,终止试验[21]。

表3 混凝土的配合比Tab.3 Mix Proportion of Concrete

图4 加载装置和测点布置
2 试验结果与分析
2.1 宏观破坏形态
图5给出了各试件的破坏形态。从图5可以看出,与传统方钢管混凝土试件(1号)相比,2~5号试件的破坏形态无明显差异,均呈现出受压区钢管局部鼓曲的破坏形态。这说明偏心距相同时,试件是否内置角钢以及取钢率、角钢至钢管内壁净距变化均不会对试件的破坏形态产生趋势性影响。

图5 试件破坏形态
试验进行过程中,各试件钢管都未出现焊缝撕裂。峰值荷载前试件无显著变化,受压侧钢管肉眼可见的局部屈曲基本都出现在峰值荷载附近。
2.2 荷载-变形曲线
各试件的实测荷载-竖向变形曲线及荷载-柱半高处侧向挠度曲线分别如图6,7所示。从图6,7可以看出:
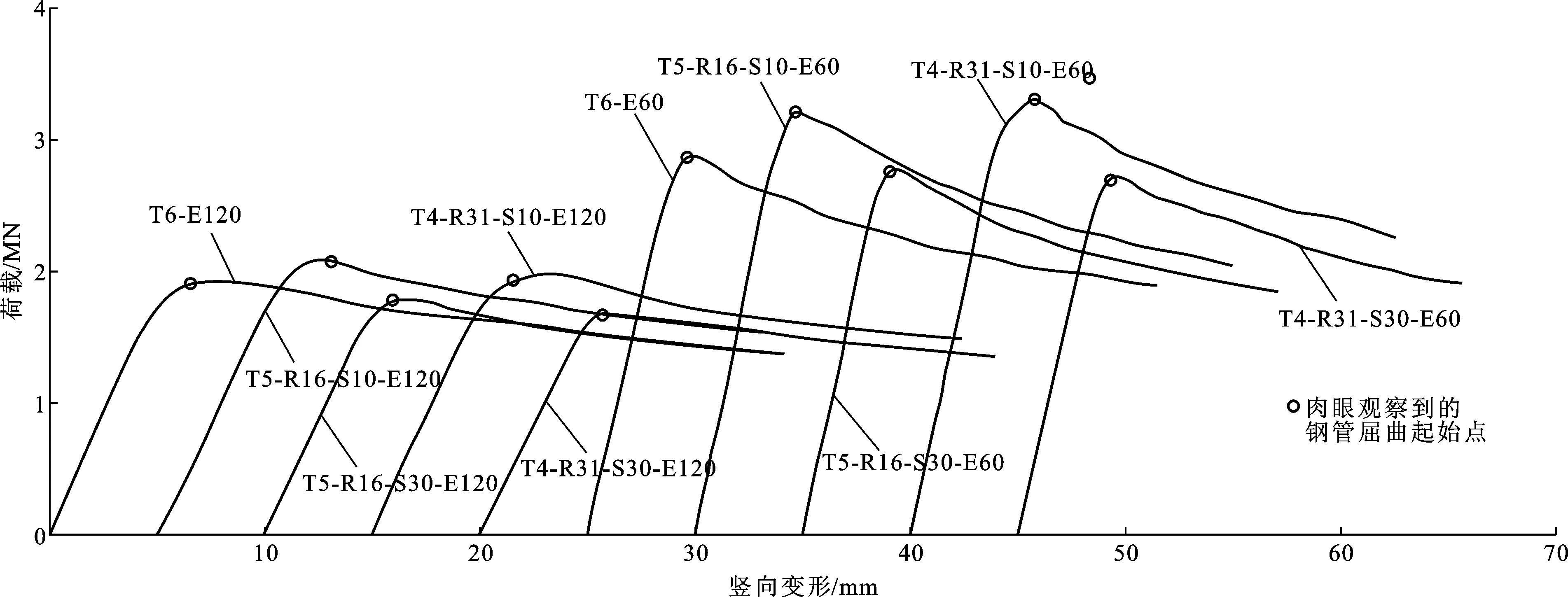
图6 实测荷载-竖向变形曲线
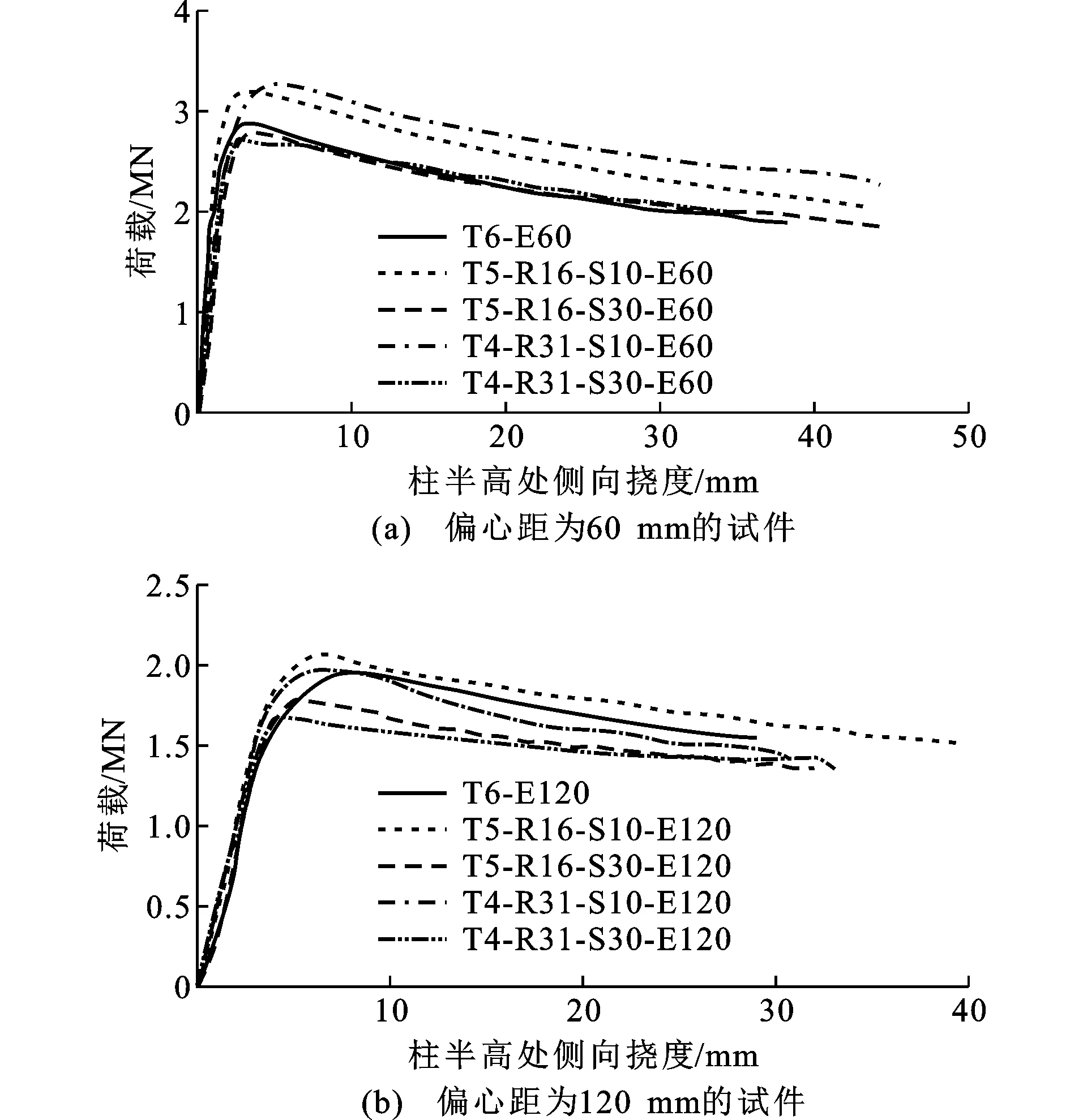
图7 荷载-柱半高处侧向挠度曲线
(1)其余参数保持不变时,取钢率从16.3%变化到30.7%对试件偏压性能的影响较为有限。这是因为尽管外部钢管钢材用量的减少一定程度上会削弱试件的偏压性能,但内部高强角钢用钢量的提升(角钢在钢管混凝土的约束下不容易发生屈曲)又对试件的偏压性能有所改善。试件受到上述2种因素的共同影响,因此总体上偏压性能变化有限。
(2)其余参数保持不变时,角钢到钢管内壁净距从30 mm减为10 mm,能够提升相应试件的偏压性能。这是因为该净距相对较小时,角钢到试件中性轴的距离变大,角钢的抗弯贡献随之增大,进而提升试件的偏压性能。
(3)偏心距从60 mm增至120 mm会导致试件的刚度及承载能力大幅降低。
2.3 偏压承载力、屈服荷载、等效刚度和延性系数
表4列出了所有试件的偏压承载力、屈服荷载、等效刚度和延性系数。表4中除偏压承载力外,其余三者的值都是基于试件的荷载-竖向变形曲线来确定的。屈服荷载的确定方法为[22]:延长原点和75%峰值荷载点的连线,并与经过峰值荷载点的水平线交于一点F,过点F作垂线,该垂线与试件实测荷载-竖向变形曲线的交点定义为屈服点,屈服点所对应的纵坐标视为屈服荷载值。等效刚度指原点与75%峰值荷载点之间连线的割线刚度[23]。延性系数μ=Δ0.85,2/Δ0.85,1,Δ0.85,1和Δ0.85,2分别为峰值荷载前后2个85%峰值荷载点相对应的竖向变形。从表4可以看出:
(1)相比于传统无内置角钢的钢管混凝土试件,在总用钢量基本不变的情况下,当角钢到钢管内壁净距为10 mm时,试件的偏压承载力提升2.7%~14.9%;当该净距为30 mm时,试件的偏压承载力均降低,且降幅随取钢率增加近似呈比例增大(当偏心距为60 mm时,取钢率16.3%和30.7%所对应的承载力降幅分别为2.7%和5.2%;当偏心距为120 mm时,取钢率16.3%和30.7%所对应的承载力降幅分别为7.3%和12.9%)。表5给出了试件偏压承载力提升幅度为0%时的假想工况,假想工况所对应的参数取值(取钢率、角钢到钢管内壁净距)是基于各试件的实测提升幅度,采用线性插值得到的。对表5所示假想工况利用最小二乘法进行拟合(取钢率-36.6%不切实际,在计算过程中已被剔除),得到偏压承载力提升幅度为0%时所对应的参数界线(图8)。图8中网格区域表示承载力有所提高,该区域以外代表承载力降低。实际工程中,通过合理选用取钢率及角钢到钢管内壁净距,可使内置高强角钢试件的偏压承载力与传统无内置角钢试件近似相等。
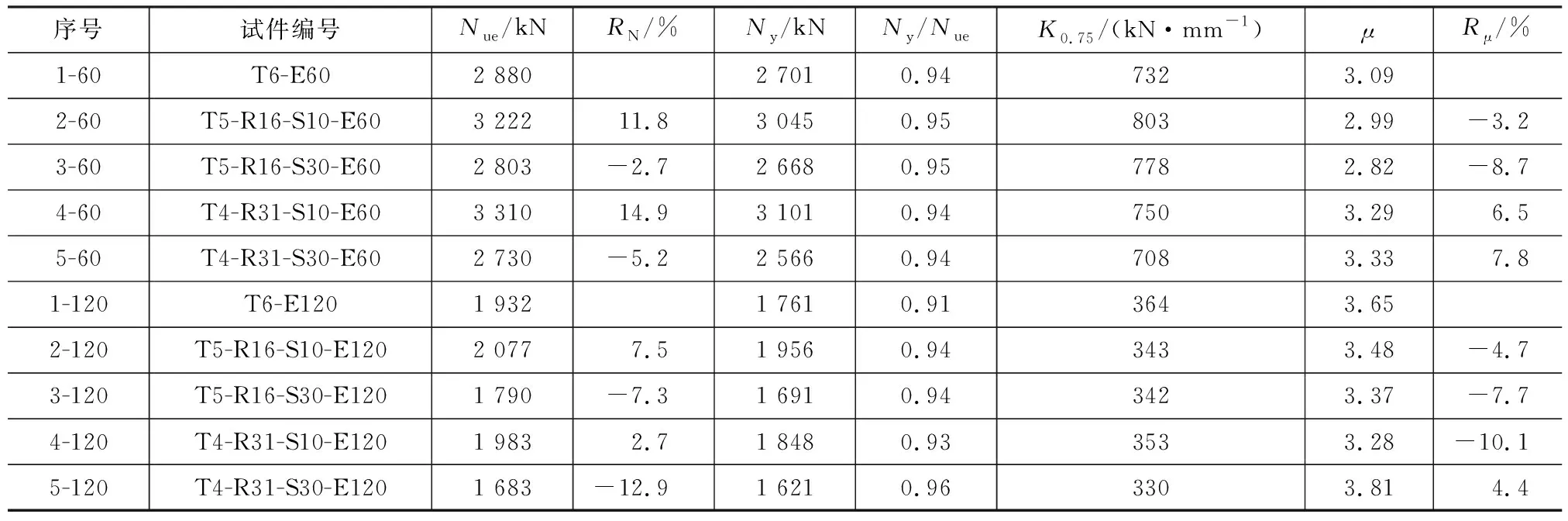
表4 试件的偏压承载力、屈服荷载、等效刚度和延性系数Tab.4 Eccentric Load Bearing Capacity, Yielding Load, Equivalent Stiffness, and Ductility Coefficient of Specimens
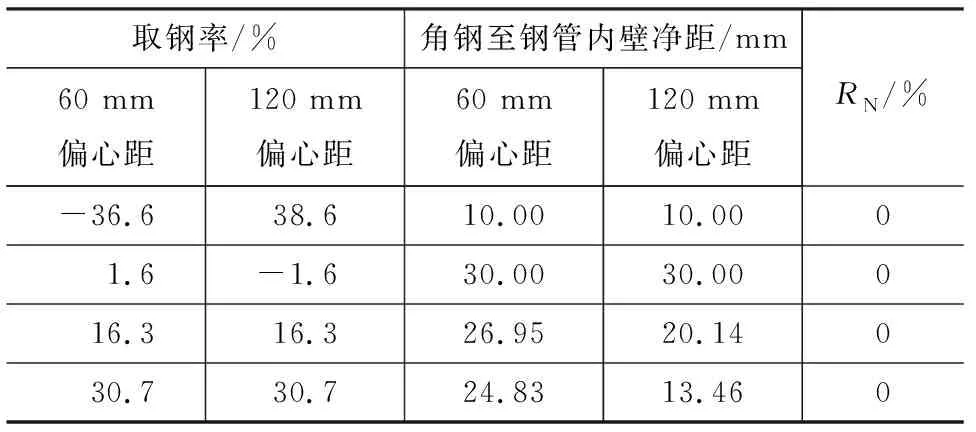
表5 偏压承载力提升幅度为0%时所对应的假想工况Tab.5 Hypothetical Situations Related to Increase of Eccentric Load Bearing Capacity Being 0%
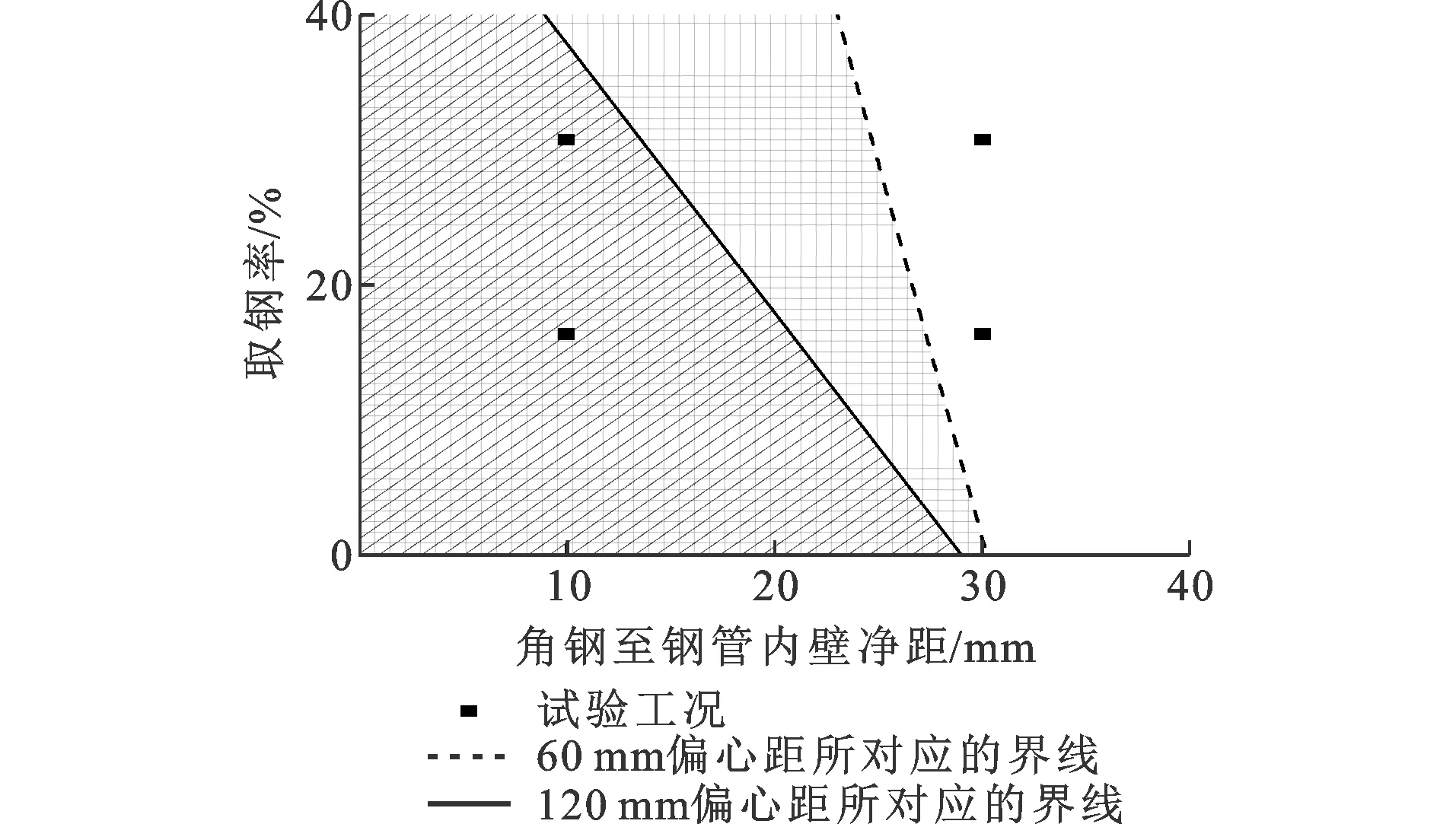
图8 偏压承载能力的提升区域预测
(2)与取钢率相比,角钢到钢管内壁净距对试件偏压承载力的影响更为显著。这是因为后者的变化会改变角钢到试件中性轴的距离,进而对试件的截面抗弯能力产生影响;取钢率增加和外部钢管钢材用量降低对偏压性能产生的不利影响可以通过受拉区及受压区面积的适当扩大得到一定弥补。
(3)对于2种偏心距,都有部分内置高强角钢试件的偏压承载力高于传统无内置角钢试件。这是因为总用钢量基本不变的情况下,当角钢至钢管内壁净距相对较小时,尽管外围钢材减少,但可通过受拉区及受压区面积的适当扩大而得到一定补偿;另一方面,受压区高强角钢因受到钢管混凝土的约束,其受压屈曲得到缓解,也对受压区钢管屈曲所造成的负面效应起到了一定对冲。
(4)内置高强角钢的钢管混凝土试件屈服荷载与峰值荷载之比和传统无内置角钢试件大致相当。
(5)相比于传统无内置角钢试件,内置高强角钢试件的等效刚度在±10%范围内波动。总体来看,取钢率在16.3%~30.7%范围内变化及角钢到钢管内壁净距在10~30 mm范围内变化,都不会对试件的等效刚度产生显著影响。
(6)相比于传统无内置角钢试件,内置高强角钢试件的延性系数变化幅度在-10.1%~7.8%之间。由于试件的变形量通常具有较大随机性,可近似认为这2种试件的延性总体相当。这是因为尽管外围钢材用量减少会导致试件延性有一定程度的劣化,但内部高强角钢由于受到四周混凝土和钢管的共同约束,其受压屈曲得到明显缓解,又对该弱化效应带来一定对冲。这2种因素的共同作用使得2类试件的延性总体上差别有限。
2.4 应变分析
图9给出了不同试件的荷载比-钢管纵向应变比曲线,其中荷载比指试件所受荷载与其峰值荷载之比,钢管纵向应变比为试件实测纵向应变与钢管钢材的单轴屈服应变之比。从图9可以得到:①在偏心距保持不变的情况下,内置高强角钢试件的曲线上升段和传统无内置角钢试件近乎一致;②当试件偏心距为120 mm时,其钢材受拉屈服大多发生在峰值荷载附近;当试件偏心距为60 mm时,其钢材受拉屈服均发生在峰值荷载之后。
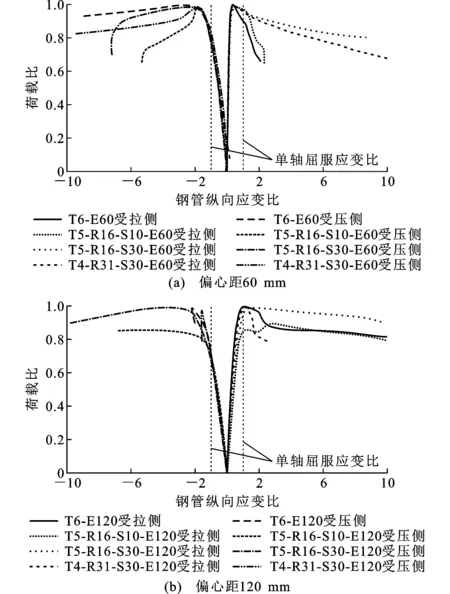
图9 荷载比-钢管纵向应变比曲线
图10给出了不同荷载P水平下典型试件的横向应变沿截面高度的分布情况。由图10可知:①加载到70%峰值荷载之前,试件横向应变沿截面高度近似呈线性分布,之后受压区横向应变迅速增长,受拉区横向应变相对而言变化甚微;②达到峰值荷载时,越靠近受压区边缘,横向应变越大,说明钢管对混凝土的约束作用越强,所以在计算分析时有必要将该约束作用的空间分布予以适当考虑。
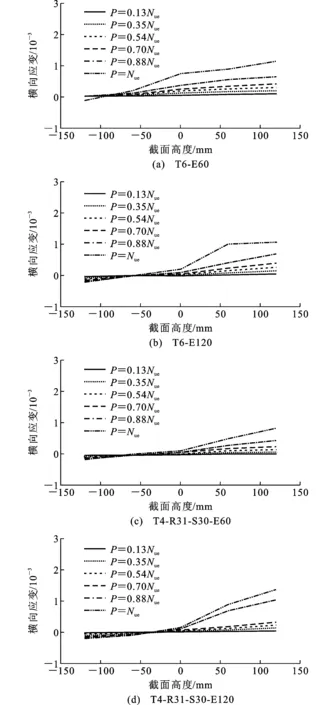
图10 横向应变沿截面高度的分布
图11给出了典型试件的角钢Mises应力-竖向变形曲线,其中角钢Mises应力由式(1)[24]计算得到,虚线代表峰值荷载时试件的竖向变形,即峰值变形。由图11可知:①偏心距为60 mm的试件达到其峰值变形时,受压侧角钢的Mises应力分别为756 MPa和851 MPa,已超过其屈服强度(735 MPa);
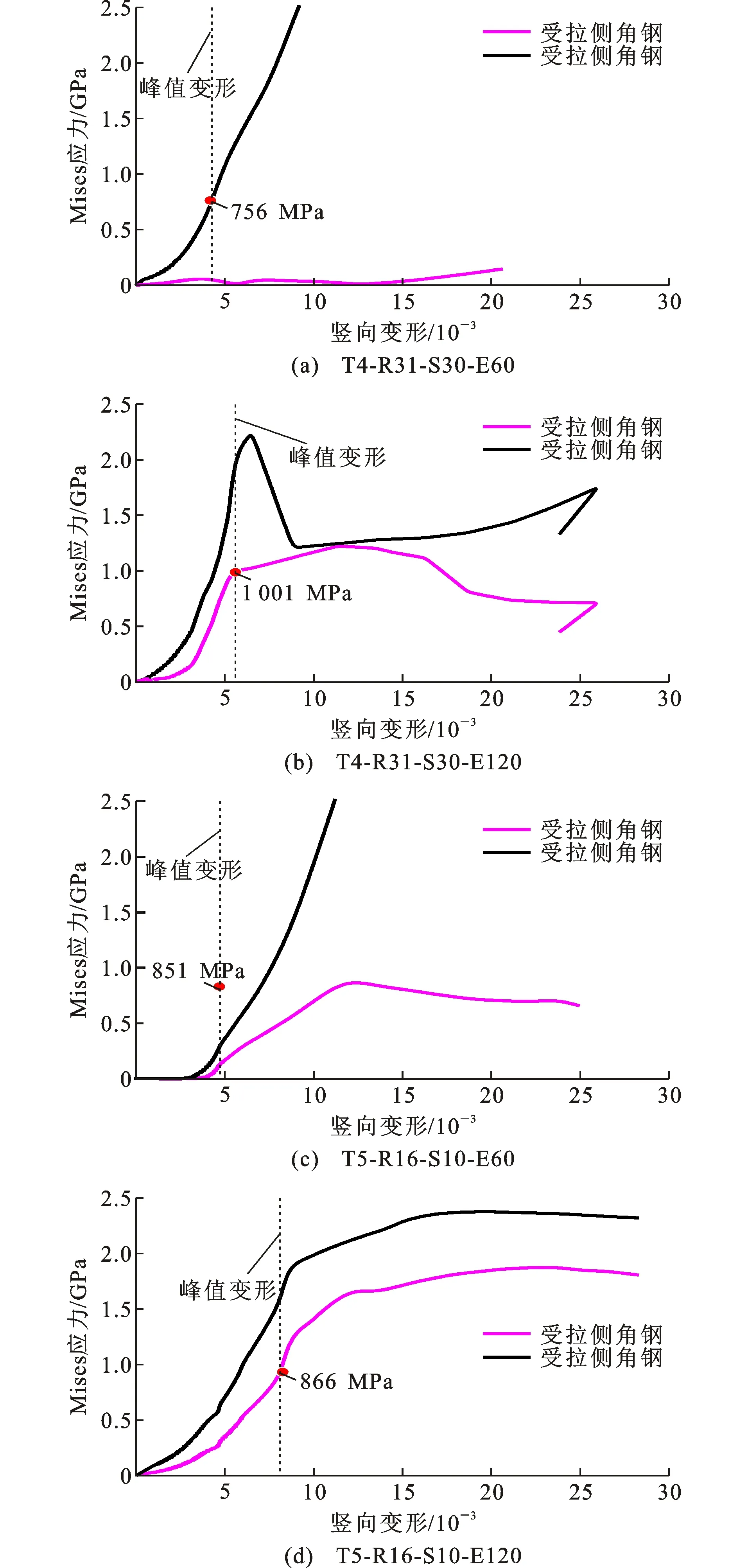
图11 角钢Mises应力-竖向变形曲线
②偏心距为120 mm的试件达到其峰值变形时,受压侧与受拉侧角钢的Mises应力均已达到屈服强度。这说明本文试件达到偏压承载力时,受拉区或受压区高强角钢的强度已充分发挥。
(1)
式中:σMises为角钢Mises应力;E为角钢的钢材弹性模量;εx和εy分别为角钢的横向和竖向实测应变。
3 偏压承载力实用计算方法
在前人研究成果的基础上,下面对内置角钢的方钢管混凝土柱偏压承载力计算进行初步探讨。共考虑3种计算方法。
计算方法1。按照极限平衡理论的叠加原则,把柱截面分为方钢管、混凝土和角钢3部分,同时考虑外侧钢管对混凝土的约束效应及钢管横向受拉导致的轴向承载力折减,经过简化得到相应短柱的轴压承载力计算公式[25]。在此基础上,从大量试验数据中得出长细比对极限承载力的影响系数φ1的经验计算公式,再近似利用双曲线描述偏心距对柱偏压承载力的影响,最终得到偏压承载力计算公式[18]
Nu=φlφeN0
(2)
N0=Acfc+1.2Atfyt+Asfys
(3)
(4)
(5)
式中:Nu为偏压承载力;N0为轴压承载力;φl和φe分别为考虑长细比和偏心率影响的折减系数;At,Ac,As分别为方钢管、核心混凝土及角钢的横截面面积;fys,fyt分别为内部角钢的屈服强度和方钢管的屈服强度;L0为柱的计算长度。
计算方法2。通过考虑钢管对混凝土的约束效应,对核心混凝土应力-应变关系中的下降段参数及峰值应变进行了修正,再对有限元计算结果进行回归分析,得到轴压承载力实用计算公式[26]。在此基础上,考虑试件截面在偏压作用下的塑性发展状态,采用条带法迭代求出偏压承载力和N-M(轴力-弯矩)关系,再利用三折线近似描述该N-M关系,最终提出偏压承载力的实用计算方法。此方法相对繁琐,详细过程见文献[26],在此不再赘述。需指出的是,本文计算时该文献所提钢骨已被替换为高强角钢。
计算方法3。将方法2的轴压承载力按式(6)进行计算[27]。方法2在确定截面塑性发展系数时,尽管套箍系数和配骨指标已体现了钢材截面面积的影响,但对钢管与钢骨(本文高强角钢)之间的空间位置考虑不足。为此,本文借鉴文献[26],引入系数γ1对方法2的截面塑性发展系数进行修正,并利用回归分析得到γ1的计算公式[式(7)]。除上述变动外,方法3的计算过程与方法2相同。
N0=αAcfc+βAtfyt+Asfys
(6)
(7)
(8)
(9)
(10)
式中:α和β分别体现方钢管对核心混凝土的约束作用和钢管横向受拉对轴向承载力的削弱作用;ζ为截面塑性发展系数;It,Is,Ic分别为钢管、角钢和混凝土的截面惯性矩;θ和ρ分别为套箍系数和配骨指标,按文献[25]计算。
运用上述3种方法,分别对本文试件的偏压承载力进行计算。表6给出了偏压承载力计算值与试验值的对比,其中Nu,1,Nu,2,Nu,3分别代表方法1、方法2和方法3偏压承载力的计算结果。由表6可知:采用方法1所得计算值与试验值之间的相对误差较大,达到-52.1%~-37.5%;方法2的精度比方法1有一定改善,相对误差缩减至-29.4%~-6.4%;相比于前2种方法,本文改进提出的方法3精度有明显提升,相对误差为-11.3%~11.3%。
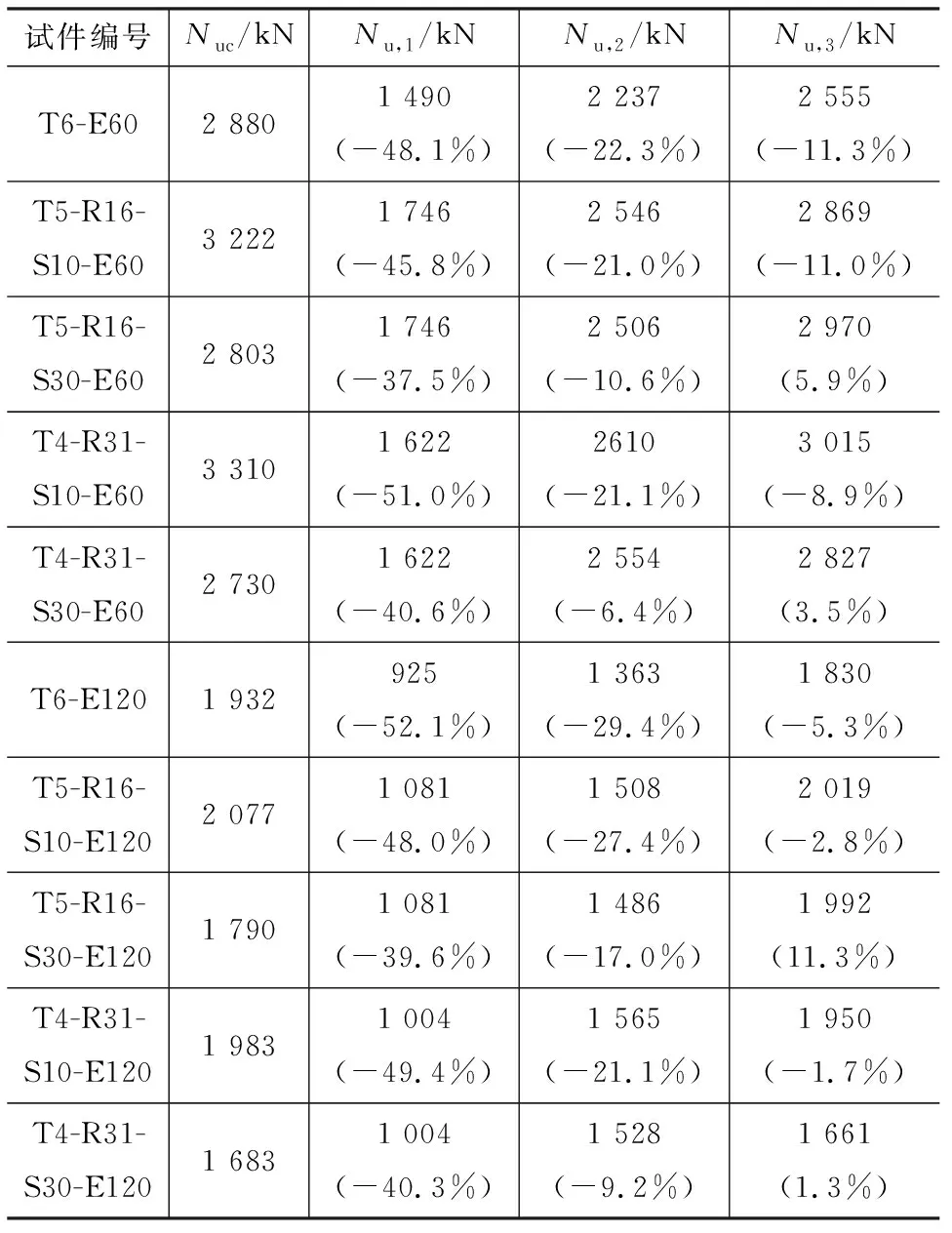
表6 偏压承载力计算值与试验值的对比Tab.6 Comparison Between Calculated and Measured Values of Eccentric Load Bearing Capacity
4 结语
(1)相比于传统无内置角钢的方钢管混凝土柱,当总用钢量基本保持不变且角钢到钢管内壁净距相对较小时,内置高强角钢的方钢管混凝土柱偏压承载力有一定提升,而当该净距相对较大时,后者的偏压承载力会有所降低。实际工程中,只要合理确定取钢率及角钢到钢管内壁净距,可使2类柱的偏压承载力总体相当。
(2)相比于取钢率,角钢到钢管内壁净距对内置高强角钢的方钢管混凝土柱偏压承载力的影响更为显著。
(3)总用钢量相同时,相比于传统无内置角钢试件,内置高强角钢试件的等效刚度及延性总体上改变有限。适当减薄钢管并在管内设置高强角钢不会对柱的偏压性能造成明显不利影响。
(4)对于内置高强角钢的方钢管混凝土柱,在偏压峰值荷载时,受压区或(和)受拉区的高强角钢已充分发挥其强度。
(5)总体来看,本文提出的改进内置高强角钢的方钢管混凝土柱偏压承载力实用计算方法(方法3)具有较好精度。
