HEC-HMS模型在青山河流域洪水模拟中的应用

彭楚杰

(湖南省湘潭水文水资源勘测中心，湖南 湘潭 411100)

在中国南方地区，山丘区小流域分布广泛。山丘区中小流域洪水呈现洪峰高、冲击力大的特点[1]，且流域内调蓄能力有限，在遭遇强暴雨袭击时，发生山洪灾害的可能性极高。所以，为了实现山洪灾害预警，快速推求小流域径流过程显得尤为重要。

大多数山丘区中小流域水文站网覆盖率低，长系列水文监测资料匮乏，概念性模型难以推广使用，将GIS技术与水文学原理相结合的分布式水文模型成为主要的水文应用发展方向[2]。如利用GIS等空间技术建立暴雨洪涝灾害综合指数评价模型,确定暴雨洪涝风险图[3]。美国陆军工程兵团研发的HEC-HMS分布式水文模型具备操作简单和免费开源的特点，能整合多种产、汇流及河道演算方法[4-6]，在印度蒂斯塔流域山洪灾害研究[7]、印度南部提鲁奇拉帕利市无资料地区洪水风险评估[8]以及阿尔及利亚梅克尔流域降径过程模拟[9]等中都得到了较好的实践。在中国针对HEC-HMS模型的研究主要有高程数据精度影响分析[10]、参数变化影响[11]和模型比对[12]等，同时也逐步应用于洪水预报[13]、临界雨量计算及山洪灾害预警[14-15]等领域。该模型利用网格结合DEM数据将流域划分为多个子流域，能充分考虑流域内地形与气候因素的时空差异，还原流域内产汇流物理过程，在资料稀缺流域也能得以适用[16]。

1 研究区域概况

研究区域选取青山河青山桥水文站以上流域(112°24′E～112°36′E，27°36′N～27°24′N)，青山河为涓水一级支流，全长32.0 km，流域集水面积277 km2，河流坡降0.244%；地形三面环山，东北、西北、西南地势均较高。研究区域内最高点海拔743 m，最低点海拔67 m(图1)。研究区属中亚热带季风湿润气候区，全年降水量为1 200～1 500 mm。山丘区总体植被覆盖较好，丘陵区主要以农业耕作区为主。青山河流域属中亚热带东部常绿阔叶林亚带，按植被区系划分，属华中偏东亚系。青山桥站为中小流域自动监测站，主要监测项目有降水量、水位和流量信息。水文站上游无闸坝，开发利用程度不高。

图1 青山河流域地形

2 数据处理

2.1 研究区DEM数据提取

DEM原始数据下载自地理空间数据云平台，下载的数据源为ASTGTM2_N27E112，分辨率30 m。采用ArcGIS软件中的空间分析工具提取出流域的栅格数据，并进行坐标转换与投影。运用ArcGIS软件中的HEC-GeoHMS拓展模块，对提取出的流域栅格数据进行填洼、流向、流量计算，确定提取阈值，提取出青山河的数字水系图[17]，见图2。在此基础上，将出口以上流域进行子流域划分。根据水系结构生成河网拓扑结构，并根据地形数据提取流域质心，计算最长流路；初步选取产流参数与河道演算方法，计算坡度、河长、等部分模型计算参数，导入到子流域属性图层。

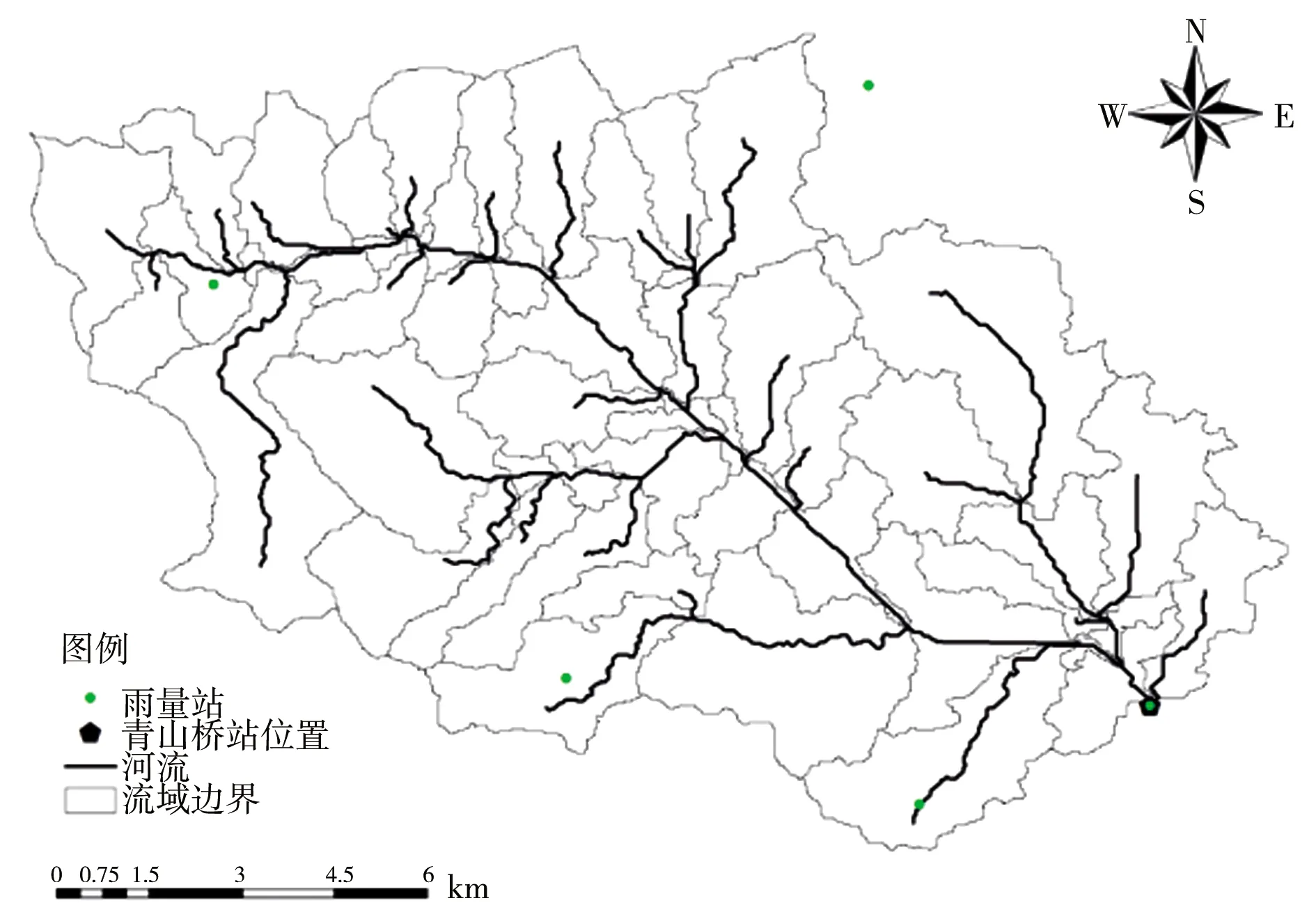
图2 青山桥水文站以上流域水系

2.2 水文资料

研究区域内有青山桥站降水量观测资料，同时，周边邻近流域有横铺、赤石和黄巢3处降水量站，积累了较长序列降水量资料。利用4站降水量资料采用泰森多边形法计算面降水量，雨量站分布泰森多边形代表面积分配见图3。青山桥站自2016年建站以来有部分实测洪水过程流量资料，可用于模型参数率定及预报检验，利用HEC-DSSVue数据处理工具将计算时段流量数据导入模型，进行参数试算与精度对比。

图3 青山河流域雨量站分布及泰森多边形划分

3 模型构建

3.1 HEC-HMS模型结构

模型基础部分包括网格文件、流域模型、气象模型、控制模块、时序数据五大块。模型构建流程见图4。流域模型中包含了各子流域的坡度、高程等地理参数。在HEC-GeoHMS中根据流域地形将研究区域划分为57个子流域，并生成网格，将流域产汇流过程概化成水库、汇流、下渗等树状水系要素，概化结果见图5。气象模型可以输入雨量站点的坐标、选择面雨量统计方法，可采用雨量站时段降水数据作为输入。控制模型设定计算的起止时间及步长，也是各时序文件与其他模块单元的输入端口；时序数据是降水量数据与流量数据输入各模块的载体。在本研究中，时序文件与计算步长统一设定为1 h，通过网格划分单元计算各子流域的产流量，再进行汇流与河道演算，最后推求出流域出口断面处的径流过程。

图4 模型构建流程

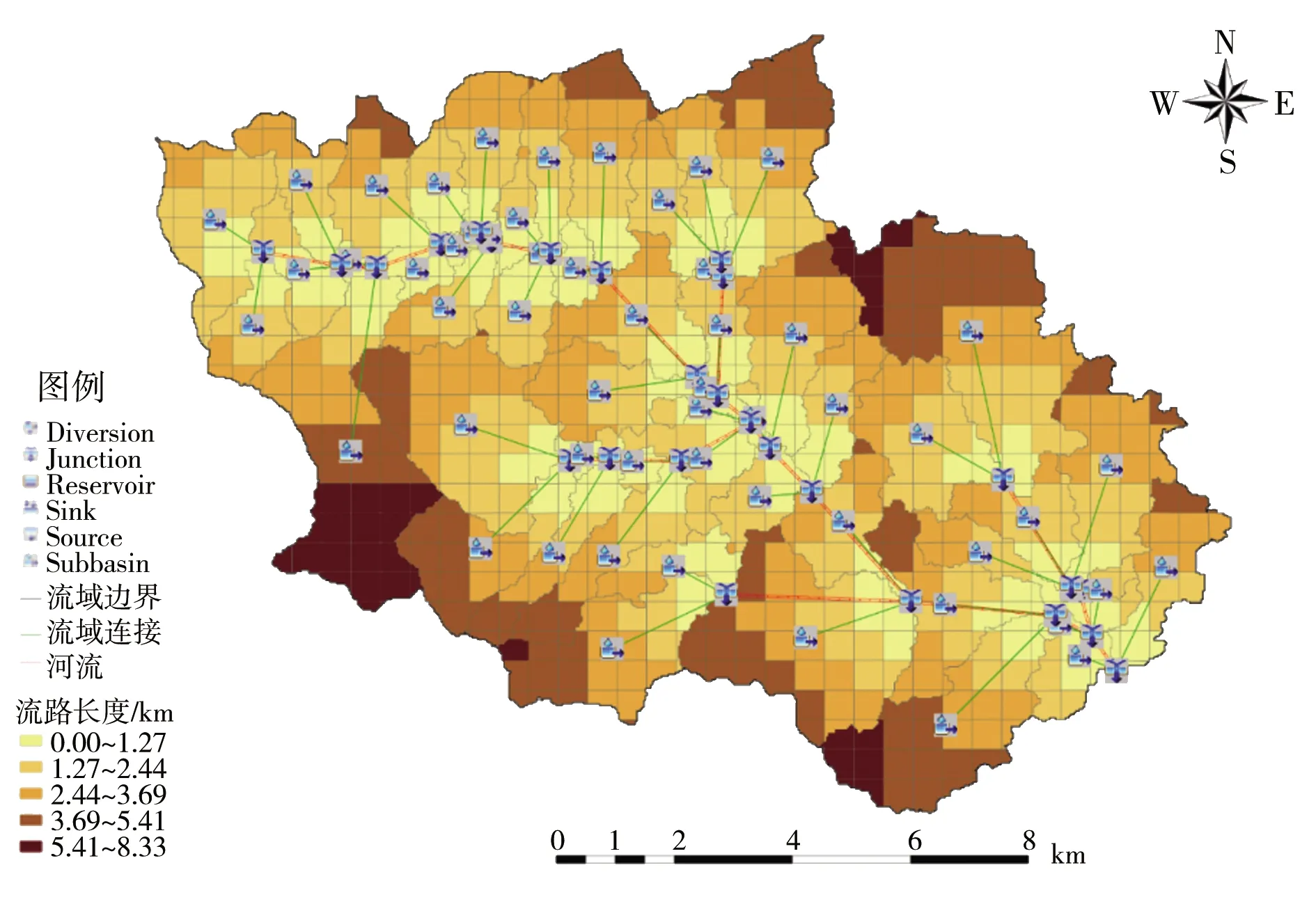
图5 流域模型概化

3.2 模型计算方法

模型中总体分径流量计算、地表径流模拟、基流与河道水流模拟4个部分。模型对各部分计算均提供了多种方法选择。

3.2.1径流量计算

集水区内不透水表面无水量损失并产生径流的部分，即为净雨，也就是径流的主要来源。模型提供了数种计算损失的方法，是以水量损失的不同计算形式来区分，本次选取初损常损法。

假设最大潜在降雨损失fc在整个降雨过程中为一恒定值。若pt是某时段内的面平均降雨深度，则时段内的净降雨pet可表示如下：

(1)

引入初始损失量I，可用于表征截留与填洼水量，还包括蒸发与下渗等其他损失量。设pi为初始降雨深度，最终在集水区内所累积的净降雨可见式(2)：

(2)

其中需要输入的参数有初损值I、损失速率与不透水率。损失速率可以从1986年Skaggs和Khaleel发表的SCS土壤分类损失速率表中查得，不透水率可以从土壤组成及土地覆盖类型数据中进行估算，再通过模型试算确定。

3.2.2地表径流模拟

地表径流过程模拟采用斯奈德单位线计算。1938年斯奈德提出了参数化单位线的方法，给出了流域特征预测单位线参数的关系[18]。输入的参数为洪峰时滞和峰值系数。洪峰时滞是单位线峰现时间与集水区质心的时间差，在斯奈德给定的标准单位线时滞方程为：

tp=5.5tr

(3)

式中tr——降雨历时；tp——洪峰时滞。

对于斯奈德单位线中的峰值系数Cp与时滞tp有如下相关关系：

(4)

式中Up——标准单位线的峰值；A——流域面积；C——转换常数。

在实际模型计算中，对于单位线的洪峰时滞估算，可采用式(5)：

(5)

式中Ct——流域区系数；L——出口到分水点的主河道长度；Lc——出口到子流域质心的长度；C同上。

峰值系数可用以表征单位降水产生的水文过程斜率，推荐取值0.3～0.8；洪峰时滞可定义为流域质心到洪峰过程之间的时间间隔，均需要采用试算的方法确定。

3.2.3基流计算模拟

非线性boussinesq基流计算法利用假定boussinesq方程用来模拟流域降水后河道水流消退的过程。具备单场所次与连续暴雨的模拟。其所设计的参数较多，其优势在于大部分参数可以通过实测数据进行确定，当然也可以进行试算求得。参数有初始基流量、孔隙率、渗透系数、流量系数临界比、特征地下流经长度。其中孔隙率与渗透系数可以根据土壤构造及覆盖情况进行估算，特征地下流径长度则可以按流域边界到河流的平均距离进行估算。

3.2.4河道水流模拟

模型提供的马斯京根法基于槽蓄方程和水量平衡原理，将水面简化为一个线性非水平面，使用分段连续演算的方式，其方程系具备二阶精度差分格式，其涉及参数较少，应用广泛。

(6)

需要设定的参数有传播时间K与权重系数X，可以从断面与水流特性依据公式进行估算，也可以通过试算得出。

(7)

X是入流和出流影响的权重系数，范围通常在0.0～0.5，亦可用式(8)进行估算：

(8)

式中 ΔL——河段长度；n——糙率；λ——转换系数；S0——河流坡降；Q0——流量。

子河段数可根据实际河段长度与时间间隔进行确定。

4 参数率定

模型建立后，需要率定每一个模块的各项参数，模型中提供了试算的功能。选择单纯形法进行迭代试算，需要为各参数选定一个初始值。目标函数采用洪峰流量误差百分比，设置容差范围及对应试算时段。采用2017—2019年5场单峰洪水过程数据进行参数试算及率定。试算参数收敛性好，模型计算稳定，最后得到一组最佳产汇流参数，摘取部分参数见表1、2。

表1 流域产流参数率定成果

表2 河道参数率定成果

5 结果分析

在2017—2019年中选取13场降水过程(含率定场次)进行模型验证。计算精度评定采用水情预报规范中要求的峰量相对误差、峰现时间误差与确定性系数(DC)[19]。由于采用的是洪峰误差百分比函数率定的参数，所以峰量相对误差值均控制较好，其中洪峰流量误差均达到了20%以内，11场达到10%以内，占总场次的85%；峰现时差均小于3 h，其中不大于1 h的9场，占总场次的69%；确定性系数只有2场小于0.7；综合评定精度等级达到甲等有2场，乙等的有9场，丙等2场。满足洪水预报的要求。洪水过程见图6，评定结果见表3。

a)201705230000

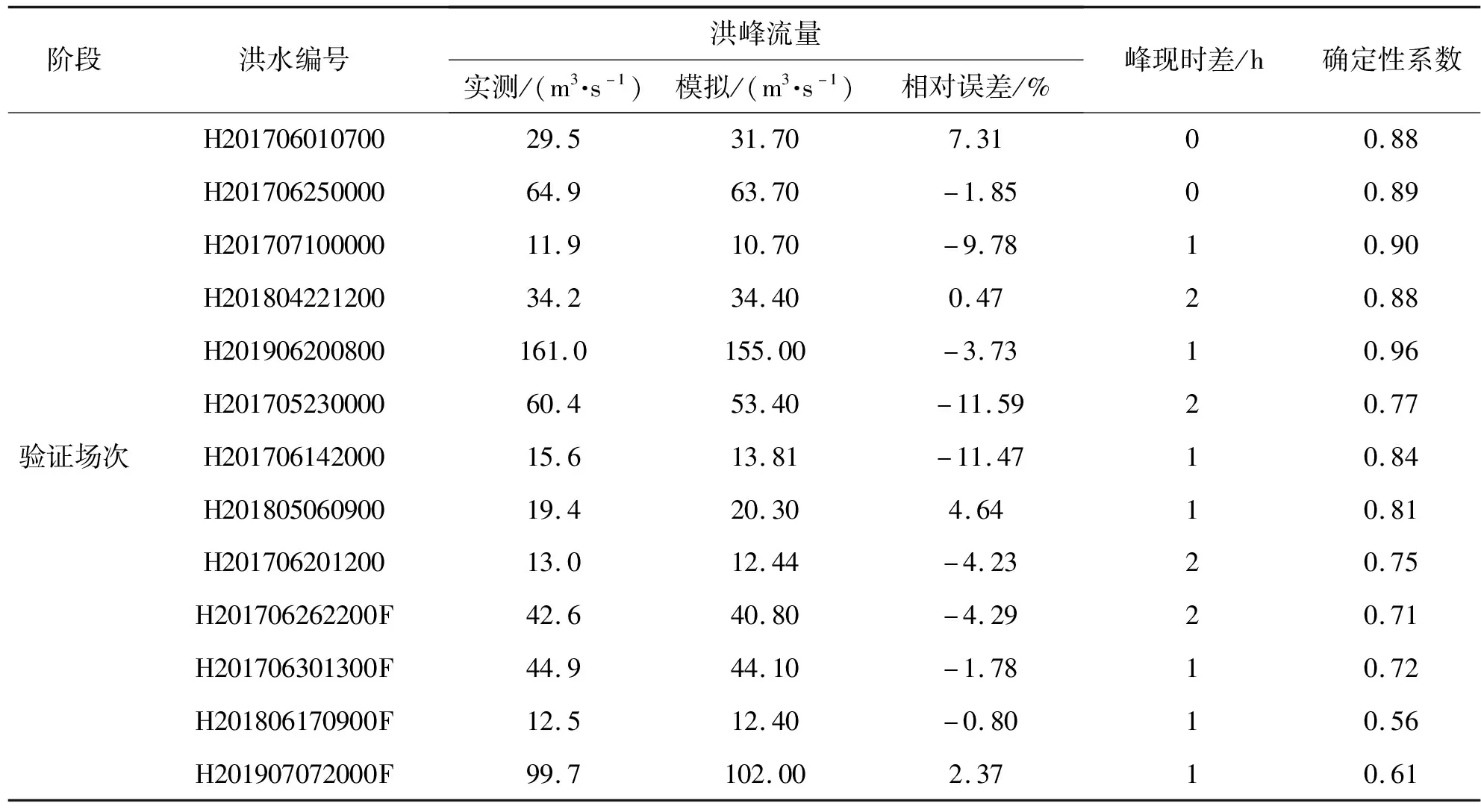
表3 模型验证成果

斯奈德单位线法核心是一个标准单峰单位线，从原理上说更适用于单峰洪水。结合径流过程线拟合情况可看出峰后无雨或少雨的单峰洪水模拟效果普遍优于复峰洪水，丙等洪水全为复峰洪水，洪号为H201806170900F的复峰洪水，确定性系数仅为0.56。洪号为H201705230000场次洪水，洪峰流量相对误差较大，因当月青山桥雨量站点存在故障，所采用雨量资料为参证所得，故有可能存在面雨量计算偏小的情况，以致于模拟结果偏小。通过对复峰洪水过程线的对比，模拟的洪水涨落尤其是消退段有较大误差，在对消退系数进行调整后作用有限，推测模型对于地表土壤层透水性与下层蓄水的模拟准确度不高，故当下层蓄水容量大时，并不能很好地还原基流消退情况。

6 结论与展望

利用DEM数据对青山河流域构建分布式洪水预报模型，利用5场单峰洪水进行参数率定，试算出一组最优参数，以13场洪水进行验证分析。

a)模型较好地还原了下垫面地形特征，将研究区域按网格化的方法分割为多个小流域进行单独计算，流域提取、模型生成、参数率定与检验均可在程序里完成，可操作性强，计算便捷。

b)初估参数经过实测洪水资料率定修正，率定过程中参数收敛无发散，模型计算稳定。以峰量误差、峰现时差、确定性系数来检验模型精度，其中洪峰流量误差均达到了20%以内，峰现时差均小于3 h，确定性系数只有2场小于0.7，综合评定结果表明，模型能满足预报要求；总体上模型对于单峰洪水的模拟优于复峰洪水，大部分过程线拟合良好，个别场次起涨段与消落段的计算有较大偏差，需要对参数做进一步调整，从山洪预警的目的出发，退水过程对于单峰洪水的影响大于复峰洪水，在实际应用中需特别注意。

c)模型对于基础资料的要求较高，特别是土壤利用数据及降水资料，现行条件下能获取到的土壤利用数据分辨率对于小流域而言精度不高，模型计算结果将产生误差；而降水资料的准确性则直接影响计算结果的准确性。

d)模型涉及的参数较多，每一步计算过程中所需要输入的参数，即便是具有实际物理意义的参数，“多参同效”的可能性依然存在，所以需要更多实测资料进行反复校正。未来将对参数敏感性进行进一步分析。

e)模型假定流域为天然状态，没有考虑流域内蓄水工程影响，实际情况下流域内存在多处蓄水工程，这也是模型计算误差的来源之一。若流域内有大型蓄、引、调水工程存在，其影响不可忽视。同时，本次研究范围为中小流域，模拟结果较好，下一步将探求在更大尺度流域上的应用。