基于EMD-LSTM-ANFIS模型的年径流预测研究

胡顺强，崔东文

(1.云南省文山州水利电力勘察设计院，云南 文山 663000；2.云南省文山州水务局，云南 文山 663000)

水文预报常表现出高噪声、动态、非线性等多重特性，研究具有较好预报精度的模型及方法目前仍是水文预报工作的重要内容。近年来，随着人工智能技术的迅速发展，BP神经网络[1-2]、GRNN神经网络[3]、Elman神经网络[4]、RBF神经网络[5]、支持向量机[6-7]、随机森林[8-9]、极限学习机[10]、神经模糊推理系统等[11]有别于传统回归分析的模型及方法已在径流预测研究中得到应用。长短期记忆(long-short term memory，LSTM)神经网络作为循环神经网络(recurrent neural network，RNN)的一个变种，克服了RNN面临的梯度消失问题，具有选择性通过新信息和选择性删除旧信息等功能，已在问题分类[12]、地下水水位预测[13]、网络流量预测[14]、股票价格预测等[15]领域得到广泛应用。LSTM优点在于适合处理与时间序列高度相关的问题，不足之处在于计算量大、耗时长。自适应神经模糊推理系统(adaptive network based fuzzy inference system，ANFIS)有机融合了神经网络的学习机制和模糊系统的语言推理能力等优点，具有较强的学习能力和表达能力，已在风电出力[16]、发电功率[17]、蓄电池[18]预测及优化控制[19]、故障诊断等[20]领域得到应用。ANFIS通过将神经网络与模糊推理有机结合起来，既发挥二者优点，又弥补各自不足，具有较好的应用效果，尤其是在消除噪声干扰、提高预测精度等方面具有广泛的应用。

径流时间序列预测是指利用径流历史数据建立预测模型来挖掘径流的变化规律，是径流预测研究中的重要内容。由于径流时间序列预测受天文、气象、地理和人类活动的影响，变化十分复杂，传统LSTM、ANFIS单一模型已不能满足径流时间序列预测的精度需求。为进一提高径流预测精度，充分利用经验模态分解(Empirical Mode Decomposition，EMD)、LSTM和ANFIS各自优点，本文研究提出一种基于EMD-LSTM-ANFIS径流预测模型：①利用EMD对径流时间序列数据进行非平稳及非线性处理，将径流序列数据分解成多个更具规律的分量序列；②针对每个分量序列，利用自相关函数法(Autocorrelation Function Method，AFM)、虚假最邻近法(False Nearest Neighbor，FNN)求解延迟时间和嵌入维数，相空间重构预测模型的输入向量；③选取合适的LSTM或ANFIS模型对各分量序列进行预测，建立EMD-LSTM-ANFIS径流预测模型，并构建EMD-LSTM、EMD-ANFIS、LSTM、ANFIS作对比预测模型；④利用云南省龙潭站年径流预测实例对EMD-LSTM-ANFIS、EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型进行检验及对比分析，旨在验证EMD-LSTM-ANFIS模型用于径流预测的可行性。

1 EMD-LSTM-ANFIS预测建模方法

1.1 EMD原理

EMD是Huang于1998 年提出的一种信号处理方法，该方法能够将非平稳非线性数据转为平稳线性数据，使其分解为较简单的固有模态函数(Intrinsic Mode Function，IMF)，各个IMF均相互独立且有较强的规律性。EMD步骤如下：由时序数据x(t)的局部极大极小值确定其上包络线和下包络线；利用x(t)减去均值包络线得到第一个IMF序列分量c1(t)；将剩余分量作为新的时间序列，重复采用EMD方法获得各个IMF子序列和1个残余序列[21-22]。表达式如下：

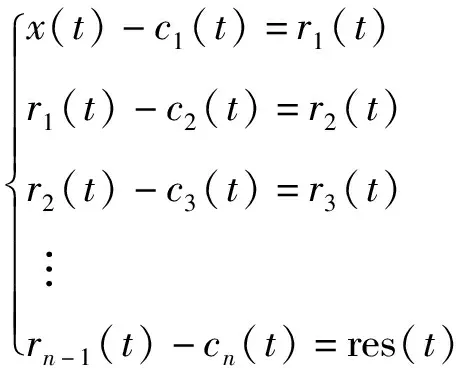
(1)

式中cn(t)——第n个IMF序列分量；rn-1(t)——第n-1次采用EMD方法分解后的剩余分量；res(t)——最终残余分量。

1.2 LSTM神经网络

LSTM神经网络是一种具有记忆功能的特殊循环神经网络(recurrent neural network，RNN)，它通过精心设计“门”结构，避免传统RNN产生的梯度消失与梯度爆炸问题，能有效地学习到长期依赖关系，在研究时间序列问题时表现出较强的优势[14-15,23]。

LSTM模型通过输入门(input gate)、遗忘门(forget gate)实现单元状态c状态的控制，通过输出门(output gate)来控制单元状态ct有多少输出到LSTM的当前输出值ht。设输入序列为(x1,x2,…,xT)，隐含层状态为(h1,h2,…,hT)，则在t时刻有：

it=σ(Whiht-1+Wxixt+bi)

(2)

ft=σ(Whfht-1+Whfxt+bf)

(3)

ct=ft·ct-1+it·g(Whcht-1+Wxcxt+bc)

(4)

ot=σ(Whoht-1+Woxxt+Wcoct+bo)

(5)

ht=o·g(ct)

(6)

式中it、ft、ot——输入门、遗忘门和输出门；ct——cell单元；Wh——递归连接权重；Wx——输入层到隐含层权重；bi、bf、bc、bo——各函数的阈值；σ(·)、g(·)——sigmoid函数和tanh函数；·——向量内积。

为使LSTM满足预测目的，需加上一个线性回归层，即：

yt=Wyoht+bo

(7)

式中yt——最终预测结果的输出；bo——线性回归层的阈值。

1.3 ANFIS推理系统

ANFIS是一种融合模糊逻辑和神经元网络的新型模糊推理系统，通过反向传播算法和最小二乘法调整前提参数和结论参数，并产生If-Then规则来实现复杂推理。ANFIS 结构一般表示为[11,24-25]：

(8)

式中x、y——输入；A1、B1、A2、B2——模糊语言；a1、b1、c1——规则1的结论参数；a2、b2、c2——规则2的结论参数；f1、f2——规则输出。

通常ANFIS 模型由5层数学模型组成[23-24]。

a)第1层,通过隶属度函数对输入变量模糊化，传递函数可以表示为：

(9)

式中μAi(x)——x的隶属度函数；di、σi——条件参数。

b)第2层,分别计算各个规则下的激励强度，即:

(10)

式中μBi(y)——y的隶属度函数。

c)第3层,对各条规则的适用度进行归一化处理，即：

(11)

d)第4层,计算第i条规则对总输出的贡献比例，即：

(12)

e)第5层,计算所有规则的输出之和，即

(13)

在给定条件参数后，ANFIS 输出可以表示成结论参数的线性组合：

(14)

式中θ——由元素构成的结论集合 {a1,b1,c1,a2,b2,c2}，为求解Aθ-f2值最小情况下的结论参数向量。

1.4 EMD-LSTM-ANFIS建模流程

EMD-LSTM-ANFIS预测实现步骤简述如下，流程见图1。

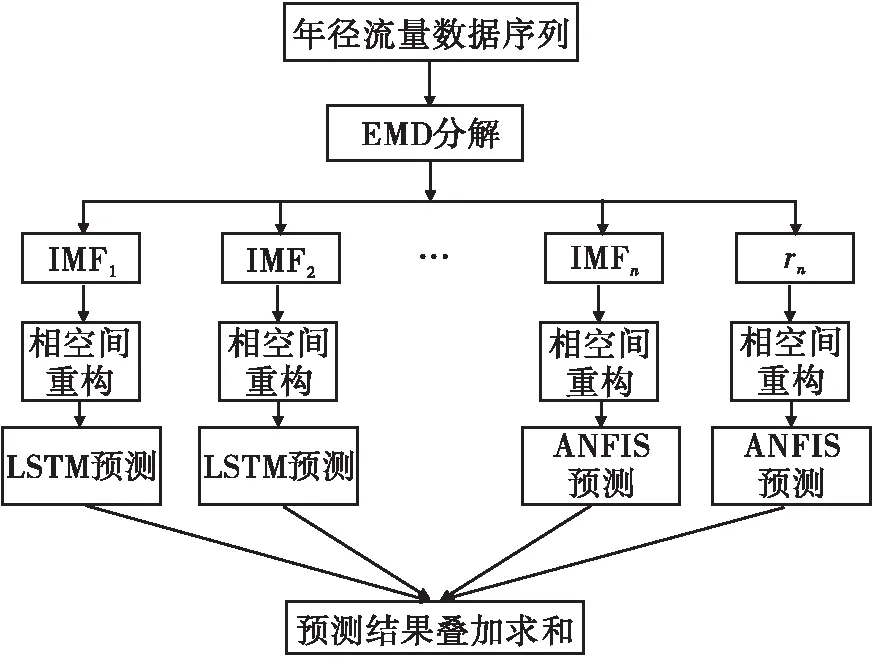
图1 径流预测流程

步骤1 将径流时间序列进行EMD分解，得到若干个IMF分量和一个剩余分量。

步骤2 通过AFM和FNN法确定实例年径流序列数据的延迟时间和嵌入维数，分别构造各个IMF分量和剩余分量res的输入向量，并合理划分训练样本和预测样本。

步骤3 选择合适的LSTM模型或ANFIS模型对经相空间重构后的各个IMF分量和剩余分量res进行训练和预测。

步骤4 对各IMF分量和剩余分量预测结果叠加获得实例年径流预测最终结果。

2 实例应用

2.1 数据来源

云南省龙潭站位于文山县攀枝花镇，属红河流域泸江水系盘龙河，该河发源于红河州蒙自县，云南境内河长252.6 km，平均坡降8.73‰，流经西畴、马关、麻栗坡县于天保船头附近注入越南。主要支流有德厚河、马塘河、木底河、布都河、畴阳河、猛硐河等。本文数据来源于龙潭站1952—2005年共54年实测年径流序列，其变化趋势见图2。从图2可以看出，1952—2005年龙潭寨水文站年径流整体呈现减少趋势，且各阶段的波动幅度不一致，这验证了该年径流序列具有不确定性和非平稳性。

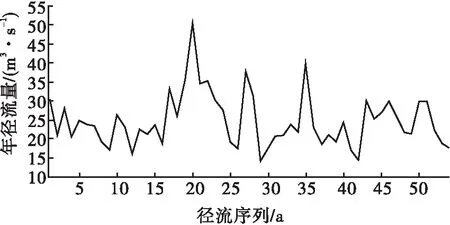
图2 1952—2005年年径流变化曲线

2.2 EMD分解

本文利用EMD方法对实例1952—2005年年径流实测时间序列进行分解，得到若干不同尺度的模式分量IMF和1个剩余分量res，见图3。

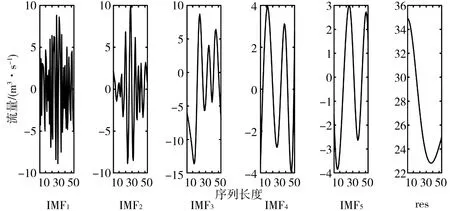
图3 1952—2005年年径流序列EMD分解结果

2.3 相空间重构

相空间重构技术有两个关键参数，即延迟时间和嵌入维数。目前确定时间序列延迟时间的方法有自相关函数法(AFM)、互信息法(MI)；确定嵌入维数的方法有虚假最邻近法(FNN)、G-P法、C-C法等。由于实例年径流实测数据序列不长，本文采用AFM、FNN法确定延迟时间和嵌入维数。经计算，实例年径流序列各IMF分量和剩余分量res的最佳延迟时间和最佳嵌入维数见表1。本文利用实例前36～41年径流实测数据作为训练样本，后10年作为预测样本。

表1 各IMF分量和剩余分量res延迟时间及嵌入维数

2.4 参数设置及预测分析

2.4.1参数设置

a)LSTM模型。LSTM采用Adam 算法训练内部参数。经调试，在隐含层神经元数H=100、训练次数E=100～200、学习速率η=0.01、梯度阈值θ=1时LSTM具有较好的预测精度。

b)ANFIS模型。通过模糊C均值聚类算法确定ANFIS网络结构和初始参数。经调试，在初始聚类数目设为2，目标误差设为0.1，分类矩阵指数设为10，最大迭代次数设为100时ANFIS具有较好的预测精度。

2.4.2各IMF分量和剩余分量res预测比较

基于表1，利用LSTM、ANFIS模型对实例各个IMF分量和剩余分量res进行训练及预测，拟合及预测结果见表2。

从表2可以看出，LSTM模型对径流序列IMF1、IMF2分量具有较好的拟合、预测效果，AFNIS模型对IMF3、IMF4、IMF5分量和剩余分量res具有较好的拟合、预测效果。本文选取LSTM、ANFIS模型分别对径流序列IMF1、IMF2分量和IMF3、IMF4、IMF5分量及剩余分量res进行组合预测，建立EMD-LSTM-ANFIS模型对实例年径流进行预测。

表2 IMF分量和剩余分量res拟合、预测相对误差

2.4.3年径流预测及比较

利用所构建的EMD-LSTM-ANFIS、EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型对实例年径流进行训练及预测，并利用平均相对误差MAPE(%)、平均绝对误差MAE(m3/s)对各模型预测性能进行评价。对于原径流序列，同样采用AFM和FNN法确定其延迟时间为1，嵌入维数为8。预测结果见表3；预测效果见图4、5。

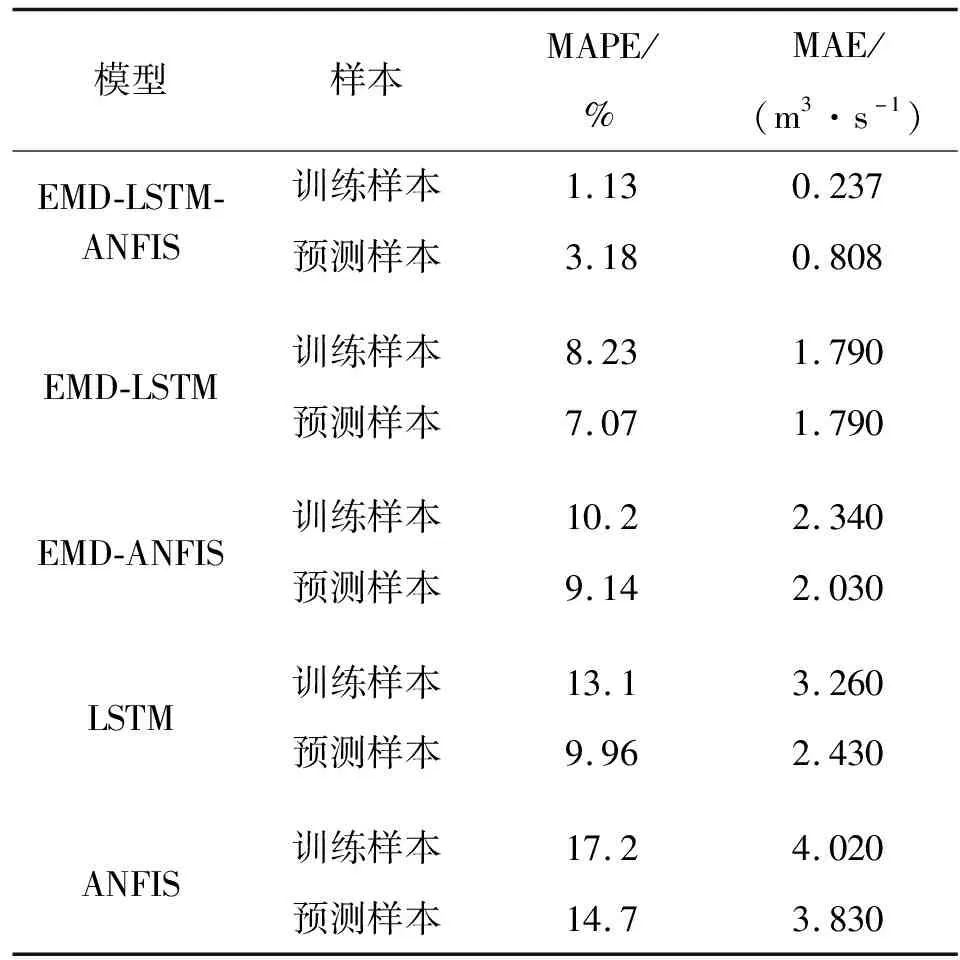
表3 各模型年径流拟合预测结果对比

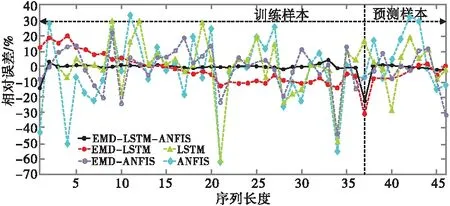
图4 年径流拟合-预测相对误差

依据表3及图4、5可以得出以下结论。

a)EMD-LSTM-ANFIS模型对实例训练样本拟合的MAPE、MAE分别为1.13%、0.237 m3/s，对预测样本预测的MAPE、MAE分别为3.18%、0.808 m3/s，拟合、预测精度均优于EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型，具有更高的预测精度和更强的泛化能力，将EMD-LSTM-ANFIS模型用于径流预测是可行的。

b)从预测样本MAPE来看，EMD-LSTM-ANFIS模型对实例径流预测的MAPE仅为3.18%，MAPE较EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型分别降低55.0%、65.2%、68.1%、78.4%，具有更好的预测精度。

c)从图4可以明显看出，EMD-LSTM-ANFIS模型对实例样本拟合、预测的相对误差值在零附近波动(除1996年相对误差较大外)，与其余4种模型相比稳定性和预测精度均较高；从图5来看，实例训练、预测结果更接近实测值，预测效果更佳。

图5 年径流拟合-预测效果

3 结论

本文基于EMD、LSTM、ANFIS模型及方法，提出EMD-LSTM-ANFIS径流预测模型，利用云南省龙潭站年径流预测实例对EMD-LSTM-ANFIS模型进行验证，并与EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型的预测结果进行比较，得到以下结论。

a)径流序列往往是非平稳、非线性的时间序列，采用EMD方法提取原始数据序列不同尺度的信息，同时分别采用AFM和FNN法确定各个信息的最佳延迟时间和最佳嵌入维数，实现了原始序列平稳化，有效改善了径流预测效果。

b)LSTM、ANFIS模型对径流序列各IMF分量和剩余分量res的拟合预测精度存在较大差异。本实例中，LSTM模型对IMF1、IMF2分量具有较好的拟合预测效果，AFNIS模型对IMF3、IMF4、IMF5分量和剩余分量res具有较好的拟合预测效果。通过二者组合建立EMD-LSTM-ANFIS模型大大提高了本实例年径流预测精度。

c)EMD-LSTM-ANFIS模型对实例径流预测的平均相对误差仅为3.18%，平均相对误差较EMD-LSTM、EMD-ANFIS、LSTM、ANFIS模型分别降低了55.0%、65.2%、68.1%、78.4%，具有更高的预测精度和更强的泛化能力，将其用于径流预测是可行的，模型及方法具有良好的应用前景。