纸筒构件受压及受拉力学性能研究

林静聪，李国鹏，陈庆军,2，陈飞豪，曾庆瀚，方淇臻，黄国贤，司徒坚文，伍良富

（1. 华南理工大学 土木与交通学院，广东 广州 510641；2. 亚热带建筑科学国家重点实验室，广东 广州 510641）

我国是一个地震多发的国家，地震常常带来巨大的经济损失和人员伤亡。在灾后永久性住所建设完成前，及时为受灾人员提供临时过渡房十分重要[1]。在现代新型轻质结构体系不断发展的同时，日本建筑师坂茂用纸筒作为结构材料建造了大量代表性的简易临时建筑，如2008 年的华林小学临时校舍，2014 年的苗苗纸筒幼儿园[2-3]等。纸筒材料作为一种绿色环保、运输方便、成本低廉、可回收利用的轻质材料[4-5]，适合作为主要材料进行灾后重置房的设计，不仅可在短时间内为灾区人民搭建避难所，且有助于我国绿色建筑的发展[6]，具有广泛的应用前景。目前，纸筒结构虽偶有应用，但其构件力学性能研究较少，因此有必要对其进行研究，为纸筒结构在实际工程的应用提供设计指引。

文献[7-8]测试了长期恒定轴向荷载对纸筒的影响，还测试了在不同条件下纸筒的张力、挠度、压缩、伸缩等。Bank 等[9]提出了一种测试纸管弯曲模量的测试方法，并通过经典的欧拉-伯努利光束理论的修正形式对试验数据进行了分析。Takanori 等[10]对6 种不同纸板和层数的纸管进行了试验研究，分析纸筒在侧向压缩载荷作用下的变形和断裂行为。解本豪[11]进行了纸筒单向拉伸试验，采用套环工艺进行了纸筒端部加强，得出某尺寸纸筒构件的受拉力学性能。

综上可知，目前纸筒结构在我国的研究很少，我国现有国家标准[12]中对纸筒构件规定的力学性能仅有径向压力，对于短期荷载下纸筒构件受压和受拉的力学性能并不明确。本文对多种规格的纸筒构件进行短期荷载下的受压和受拉试验，从构件层次研究了几何特征对纸筒构件的受压和受拉关键力学性能的影响。并通过有限元模型，对试验进行了补充，进一步明确纸筒构件的破坏形态，为纸筒结构的实用研究提供了数据支持。

1 受压构件试验

1.1 受压试件设计

为研究纸筒构件几何特征对力学性能的影响，在管壁厚度均为2.7 mm 的情况下，设置不同高度H（350、400、500 mm）和不同内径d（40m、50 mm）作为参数进行研究。为减少试验的偶然误差，每种高度和内径设置5 组对比构件，共进行了30 组纸筒受压构件的力学性能试验。

以C-350-40-1 为例来说明受压试件命名方式，其中C代表试验荷载工况为压力，350 代表试件高度H为350 mm，40 代表试件内径d为40 mm，1 代表试件为1 号试件。以不同几何特征下1 号构件为例说明不同试件的几何参数（见表1），其中I为纸筒的截面惯性矩，A为纸筒的截面面积，i为回转半径

表1 受压试件几何参数

1.2 受压构件试验装置和量测方案

试验通过液压机施加竖向静态荷载，依次对单根纸筒构件施加轴向压力，加载装置如图1 所示。液压机荷载以500 N/min 的速度增加，直至构件破坏。通过计算机与液压机连接，可实现对数据的采集。

图1 受压构件试验加载装置

1.3 受压构件试验过程

在试验过程中，各构件受压形态基本一致。一开始构件并没有明显变形，随着荷载增加，构件中部首先出现微小弯曲，如图2(a)所示。继续增大荷载，杆件顺着螺旋纹的方向发生内凹，表面出现折痕，如图2(b)所示。再继续加大荷载，折痕加深，杆件沿折痕发生折断而破坏，如图2(c)所示。纸筒构件在受压全过程中有明显的变形，表现出较好的延性。

图2 构件受压试验

1.4 受压构件试验结果

对不同高度不同内径下的各组构件进行分析，图3 给出了各对比组构件荷载位移曲线。由图3(a)—3(f)可看出，加载位移处于0~2 mm 阶段时构件基本能体现出较好的线弹性行为，在2 mm 后各构件基本上陆续进入塑性阶段，构件承载力出现下降段或波动平直段，最终达到破坏。

对试验数据处理，得到不同高度、不同内径下各组构件的受压极限承载力的平均值，将受压极限承载力除以纸筒的横截面积得到受压极限应力，将极限荷载对应下的位移除以杆件长度得到峰值应变，将线弹性段的曲线进行拟合得到弹性模量，以上数据整理如表2 所示。将受压构件受压极限承载力和极限应力随长细比变化情况如图4 所示。

图3 不同高度和内径下受压构件荷载位移曲线

表2 不同高度和内径下的各组构件受压关键力学性能指标平均值

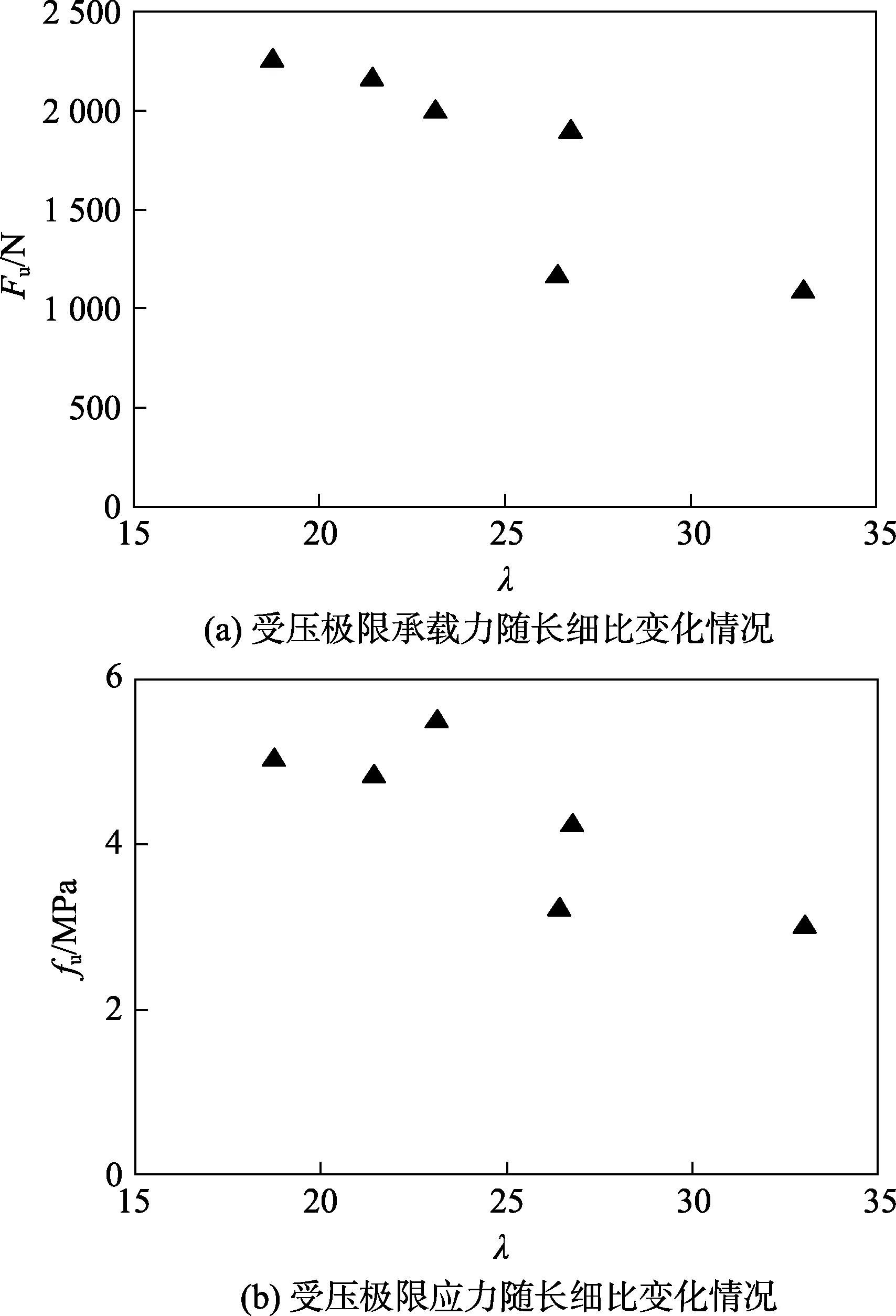
图4 受压构件关键力学性能指标随长细比变化

从构件平均受压极限承载力来看，不同构件体现的区别与对图3 的分析一致，且随着长细比增大，构件受压极限承载力基本呈下降趋势。

从构件平均受压极限应力来看，测得应力范围3.00~5.49 MPa。高度为350 mm 的构件，内径增加，构件平均受压极限应力降低，内径50 mm 构件对应增幅为–8.39%。高度为400 和500 mm 的构件，内径增加，构件平均受压极限应力提高，内径50 mm 构件对应增幅分别为50.67%和41.04%。内径为40 mm 的构件，高度增加，构件平均受压极限应力降低，高度400和500 mm 构件对应增幅分别为–41.63%和–45.42%。内径为50 mm 的构件，高度增加，构件平均受压极限应力降低，高度400 和500 mm 构件对应增幅分别为–4.01%和–15.97%。总体来看，随着长细比增大，构件受压极限应力基本呈下降趋势。

从峰值应变来看，测得的峰值应变范围0.009 9~0.016 1。从弹性模量来看，不同高度、不同直径构件测算出来的弹性模量平均值范围从0.562 GPa到0.984 GPa，所有构件弹性模量平均值为0.757 GPa。

1.5 受压构件试验结论

纸筒构件在受压全过程中有明显变形，表现出较好的延性，最终出现失稳破坏现象。试验结果表明，随着受压构件长细比增大，受压构件极限承载力和极限应力基本呈下降趋势，进一步验证纸筒构件是由于受压失稳造成的承载力失效。

2 受拉构件试验

2.1 受拉试件设计

为研究纸筒构件几何特征对力学性能的影响，在高度均为500 mm、管壁厚度均为2.7 mm 的情况下，设置不同内径d（30、50 mm）作为参数。共进行了6组纸筒受拉构件的力学性能试验。

以T-500-30-1 为例来说明受压试件命名方式，其中T代表试验荷载工况为拉力，500 代表试件高度H为500 mm，30 代表试件内径d为30 mm，1 代表试件为1 号试件。

2.2 受拉构件试验装置和量测方案

若直接对纸筒端部施加拉力，难以避免对端部有挤压，容易出现纸筒端部先破坏的情况。鉴于此，通过在纸筒两端加上保护拉头可有效减免这种情况。具体而言，可通过变截面金属圆柱体和金属箍环实现。首先在纸筒内部嵌入变截面金属圆柱体粗头，并在纸筒外围通过可调节松紧的金属箍环施加挤压力，通过加载时产生的摩擦力防止纸筒与变截面金属圆柱体粗头脱开。通过试验装置加载头夹住两端的变截面金属圆柱体细头，可以实现拉力加载。

试验通过液压机施加竖向静态荷载，依次对单根纸筒构件施加轴向拉力，装置如图5 所示。液压机荷载以500 N/min 的速度增加，直至构件破坏。通过计算机与液压机连接，可实现对数据的采集。

图5 受拉试验装置

2.3 受拉构件试验过程

在试验过程中，各构件受拉形态基本一致。随着荷载增加，纸筒开始伸长，纸筒表面绷紧。随着荷载继续增加，达到应力极限时，纸筒突然破坏，纸筒沿着斜纹发生裂开，如图6 所示。在发生断裂后，纸筒基本丧失抗拉能力。

图6 受拉试件破坏示意图

2.4 受拉构件试验结果分析

对不同内径下的各组构件进行分析，图7 给出了各对比组构件荷载位移曲线。由于内径30 mm 的3 号构件数据丢失，所以图7(a)只分析了两条曲线的结果。由图7 可看出，当加载位移到达3~5 mm 阶段时构件达到极限抗拉承载力，之后各构件承载力迅速下降，最终达到破坏。在相同高度下，随着内径增加，构件受拉极限承载力呈提高趋势。

图7 不同内径下受拉构件荷载位移曲线

对试验数据处理得到不同内径下各组构件的受拉极限承载力的平均值，将受拉极限承载力除以纸筒的横截面积得到受拉极限应力，将极限荷载对应下的位移除以杆件长度得到峰值应变，以上数据整理如表3所示。

表3 不同内径下的构件受拉力学性能指标平均值

从构件平均受拉极限承载力来看，随着内径增大，构件受拉极限承载力提高。从构件平均受拉极限应力来看，测得应力约为7 MPa。从峰值应变来看，测得的峰值应变范围0.005 9~0.011 1。

2.5 受拉构件试验结论

纸筒构件在受拉破坏前无明显征兆，体现为脆性破坏。试验结果表明，随着受拉构件内径增大，受拉构件极限承载力提高。

3 有限元模型验证

3.1 有限元模型建立

采用ABAQUS 有限元分析软件对不同尺寸的纸筒构件进行建模，以高度400 mm、内径40 mm 的构件为例，建立的模型如图8 所示。

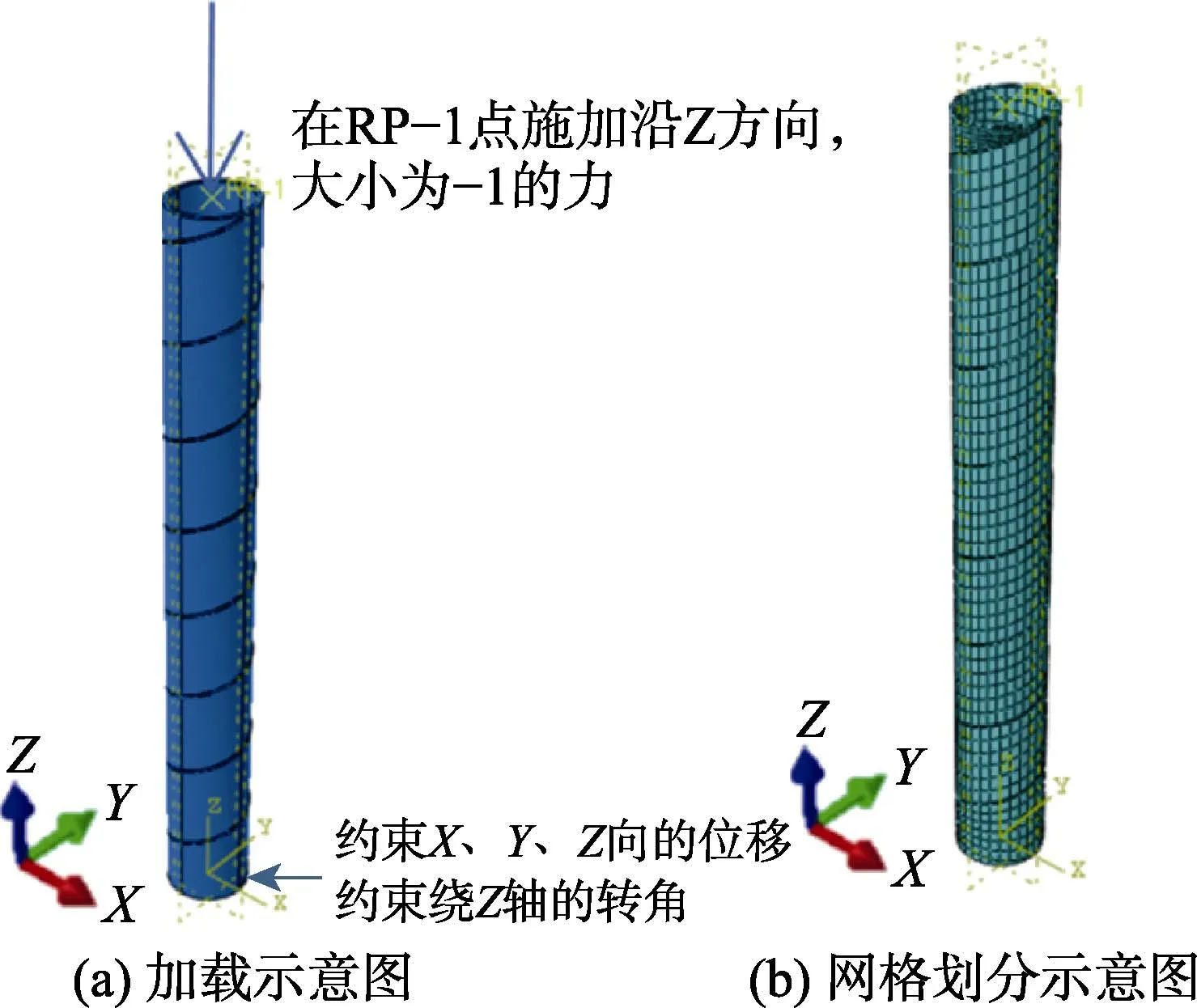
图8 纸筒构件有限元模型示意图

为更准确地模拟纸筒构件力学行为，考虑将纸筒螺旋接缝处建成螺旋线构件。通过CAD 使用布尔运算可建立圆筒和螺旋线两个部件，将其导入ABAQUS后使用tie 命令进行部件间连接，通过给螺旋线设置较低的弹模来考虑纸筒螺旋接缝薄弱区的影响。其中，圆筒部分的弹性模量使用试验测得的数据（见表2）。单元选择上，采用实体单元进行建模。创建的分析步为Linear perturbation 中的Buckle，并选用Subspace为特征值提取方法。在模型顶面中心点建立参考点，并通过coupling 将参考点RP-1 和模型顶面建立连接，在参考点RP-1 沿Z方向即模型高度方向施加大小为-1 的作用力，对模型底部施加位移约束，限制U1、U2、U3 方向的自由度，即约束X、Y、Z方向的位移。

3.2 纸筒构件弹性屈曲模拟

对6 个不同尺寸构件进行弹性屈曲分析，6 个构件的第一阶模态相近，均为中部出现横向位移，与试验现象相符合。图9 为C-400-40 构件的前三阶模态。

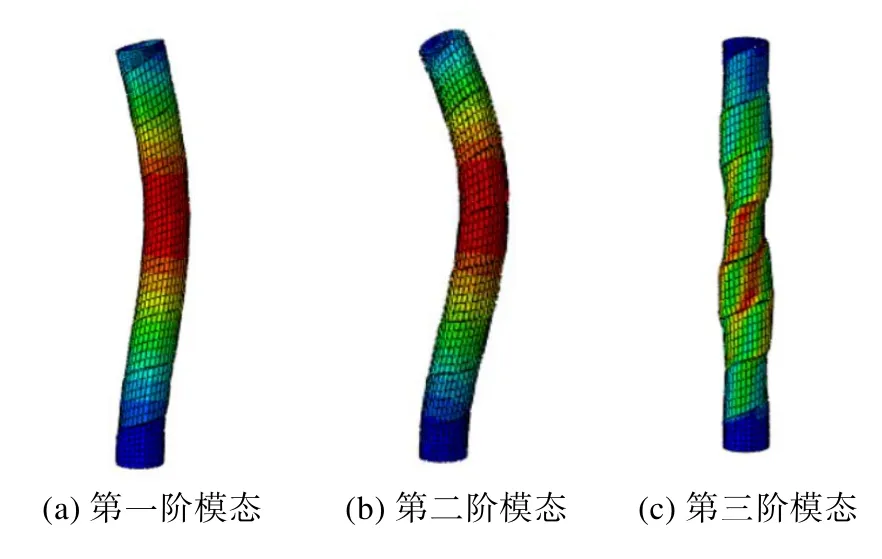
图9 构件前三阶模态（高度400 mm，内径40 mm）

依次将各构件分析结果得到的最小特征值与荷载相乘得到各构件的弹性屈曲临界荷载Fcal。表4 给出了各构件Fcal及Fcal与实验极限荷载Fexp的比值，约2~3，理论值比试验值大的原因是模拟过程中纸筒材料较为理想，无明显缺陷，其受力行为较为理想。当高度相同时，构件屈曲临界荷载随内径增加而提高；当内径相同时，构件屈曲荷载随高度增加而降低。以上两组对比均体现出随构件长细比增加其极限承载力降低的趋势。

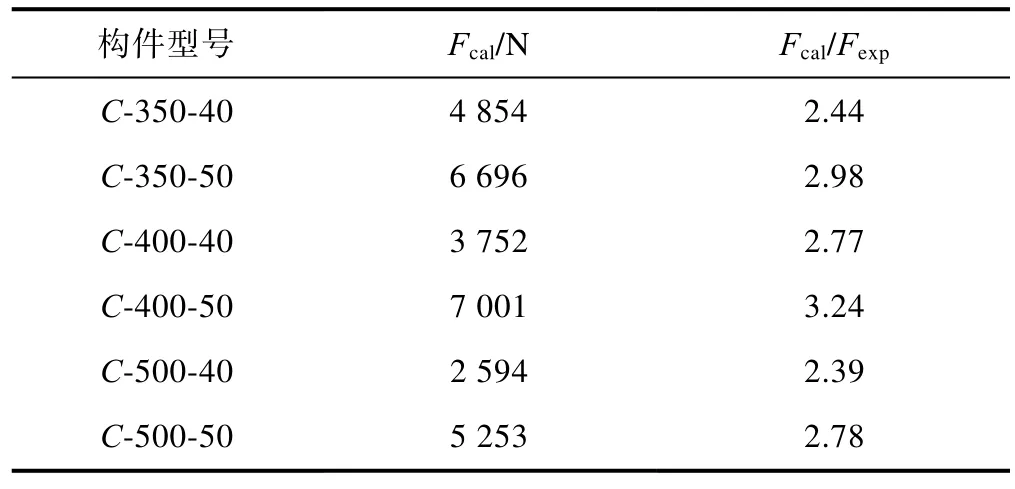
表4 各构件有限元分析弹性屈曲临界荷载

3.3 纸筒构件拉压模拟

建立高度500 mm、内径50 mm 的有限元模型，分别对参考点施加2 000 N 的轴向压力和拉力，得到位移云图如图10 所示，其形态与受压构件的早期形态及受拉构件的破坏形态均比较类似。

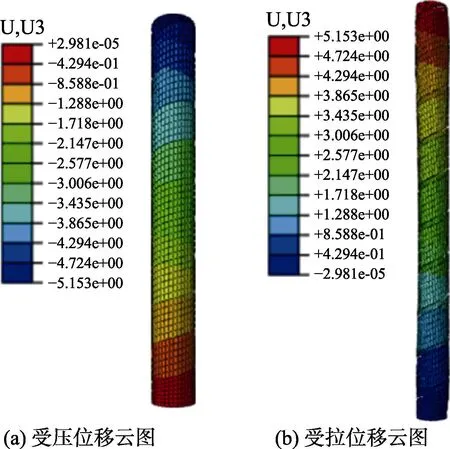
图10 纸筒构件拉压模拟

4 应用前景

此构件的基本力学性能试验可为将其应用于新型结构形式提供基础。纸筒构件具有轻便性和易拆卸性，且能够批量规模化生产，可将其应用于一种拼装式纸筒结构。这种结构由纸筒构件和金属连接头或3D 打印节点进行组装，适用于临建结构如救灾帐篷或隔离帐篷等。图11 为采用3D 打印节点连接的纸筒空间桁架结构的示意图。

图11 纸筒空间桁架结构

这种纸筒空间桁架结构的优点在于绿色环保、自重较轻、易于安装、可实现折叠和可循环使用，也可根据不同的纸筒构件尺寸要求进行节点设计。提前根据空间要求进行构件尺寸的选取和节点设计，实现工厂批量化生产。

5 结语

本文进行了6 种不同尺寸共30 组纸筒构件的受压试验和2 种不同尺寸共5 组纸筒构件的受拉试验，同时对纸筒构件进行有限元模拟，分析其弹性屈曲行为和受力行为。得出以下主要结论：

（1）所进行的6 种尺寸的纸筒构件受压试验的破坏形态均为纸筒沿着斜纹处发生破坏。试验过程中构件中部出现越来越大的横向位移，逐渐出现折痕并最终沿折痕发生屈曲破坏，承载力降低，破坏过程中体现出较好的延性。试验得到的构件极限应力3.00~5.49 MPa，峰值应变0.009 9~0.016 1。当高度相同、内径减小或内径相同、高度增加时，有限元和试验得到的构件受压极限承载力均体现出随构件长细比增加而降低的趋势。从弹性屈曲荷载与试验极限荷载的比值基本处于2~3 倍。

（2）进行的2 种尺寸的纸筒构件受拉试验的破坏形态均为沿着斜纹处拉坏。试验过程中构件在破坏前无明显征兆，更接近于脆性破坏。内径增加时，试验得到的构件受拉极限承载力增加。试验得到的极限应力约7 MPa，峰值应变0.005 9~0.009 9。

（3）通过将纸筒构件和多种金属连接头或3D 打印节点进行组装，可实现自重较轻、快速拼装、方便运输的空间结构，可适用于临建结构如救灾帐篷或隔离帐篷等。

由于试验条件限制，本文研究的纸筒数量尚不够多，所得数据存在着一定离散性，未来将增加试件数量以便进行更深入研究。