基于火焰传递函数的旋流预混火焰稳定性分析

2021-04-06余志健

燃气轮机技术 2021年1期

杨旸, 余志健

(1. 中国科学院工程热物理研究所南京未来能源系统研究院，南京 210000；2. 中国科学院工程热物理研究所先进燃气轮机实验室，北京 100190；3. 中国科学院大学，北京 100190)

贫预混燃烧是现代燃气轮机燃烧室实现低NOx排放的主要途径之一。但该燃烧室燃烧处于贫预混状态及火焰筒取消了各种气膜孔，容易产生热声不稳定问题[1]。根据瑞利准则，当压力波动相位与燃烧室内体积积分热释放率脉动相位差小于90°，且系统的阻尼不大于注入系统的能量时，则会产生热声不稳定[2]。根据先前的研究[3]，相位差可以转换为从燃料喷射位置开始到达火焰锋面处的燃料飞行时间。因此，火焰形状和混合区长度是产生热声不稳定的两个关键因素。为了控制火焰形状，燃烧室头部出口形状是除旋流数之外的重要几何控制参数。这是因为燃烧室头部出口形状会影响火焰根部的发散角，进而导致火焰形状变为V形、M形或圆锥形等。但国内外文献对该结构的影响特性报道较少。

同时，在燃气轮机燃烧室设计阶段如何采用数值方法分析不同燃烧室结构下火焰动态特性及预判火焰是否稳定，这对燃烧室结构筛选和确定具有一定作用。雷诺平均Naiver-Stokes(RANS)方法[4]和大涡模拟(LES)[5]是燃烧室设计阶段中广泛使用的两种数值方法。有了准确的燃烧模型，可以使用RANS方法在设计阶段预测燃烧室总体性能，而LES方法可以更准确地解析流动-火焰的瞬态相互作用，例如吹熄，火焰不稳定性等。但对于LES来说，由于计算的物理时间较短和缺乏相应阻抗边界条件，在燃烧室的设计阶段通常采用不可压缩LES计算[6]。

不可压LES计算忽略燃烧室出口的反向传播波，且无法获得潜在的自激热声特性。尽管如此，该方法仍可以结合系统辨识技术(system identification)，获得火焰相应的频率响应信息。通过在入口处施加适当的外部激励，可以基于放热速率的响应时间序列，通过辨识技术提取火焰传递函数(FTF)或火焰描述函数(FDF)[7-8]。该方法将火焰视为一个线性时不变系统，该系统在弱激励下可由辨识获得火焰动态响应参数。该火焰传递函数可添加至低阶热声网络模型中或三维亥姆霍兹声学模型中预估燃烧系统的稳定性[9-12]，或单独分析预判火焰发生不稳定的风险。分析火焰传递函数的方法已成功应用于西门子[13]及阿尔斯通[14]等燃气轮机燃烧室设计中，并在国际学术界得到广泛的报道。

本文提取和分析了不同燃烧室头部结构下的火焰形状及火焰传递函数。采用试验设计DoE方法对四个头部关键几何控制参数进行了分析。采用不可压大涡模拟(LES)获得精确的旋流火焰结构。通过在入口处施加弱激励，获得燃烧室热释放率动态响应，进而辨识出相应火焰传递函数，并分析了各头部结构下火焰的响应频率带及是否有不稳定风险。最终分析了燃烧室头部几何结构与火焰形状及火焰传递函数的对应关系，为设计燃烧不稳定发生风险低的低污染燃烧室提供理论指导。

1 数值方法

1.1 CFD计算

1.1.1 几何及边界条件

本文对一个单头部模型燃烧室进行大涡模拟及火焰传递函数提取。采用的旋流器为自行设计的、可采用SLM(选择性激光熔融)一体化打印成型的且适用于E级F级燃气轮机燃烧室的轴向旋流器。该轴向旋流器叶片形状如图1所示，有8个长弦叶片，叶片具有一定厚度可作为燃料通道，叶片压力面开用一个燃料孔，吸力面开有两个燃料孔，燃料孔直径选为1.2 mm。

图1 轴向旋流器

模型燃烧室完整域如图2所示，实际计算的计算域为45°扇形，采用周期性边界条件降低数值计算成本。气流方向为从左到右。掺混区长度为l，中心体末端半径为R1_TE，扩张角为α。旋流气流随扩张角向燃烧室扩散时，当气流离心力与径向压力梯度平衡时，根据涡破碎理论形成回流区。回流区的形成通常由标准旋流数控制，该旋流器速度基旋流数为0.4。边界条件如表1所示。当前几何条件下，当量比为0.514。

图2 计算域和几何结构参数

表1 边界条件

1.1.2 DoE设计表

选择了控制燃烧室头部结构的四个关键几何设计参数，如图2所示，表述如下：

(1) 中心体末端到燃烧室前墙的距离(d)；

(2) 扩张角(α)，控制气流进入燃烧室的方向；

(3) 扩张比，燃烧室截面和头部截面面积比，选择燃烧室截面半径R4为控制参数；

(4) 中心体末端半径(R1_TE)。

采用中心体半径R1作为归一化尺寸，进行二水平全因子实验设计(DoE)，共需计算16个工况，如表2所示。

表2 二水平全因子试验设计表

1.1.3 网格划分和网格分辨率

网格采用Star ccm+生成的混合网格，边界层采用三层棱柱层网格，其它区域采用多面体网格。燃料喷嘴、旋流器区、掺混区及燃烧室上游火焰位置区网格分辨率分别为0.2 mm、0.35 mm、0.5 mm和0.5 mm，以捕捉流动火焰细节。燃烧室下游网格分辨率为1.1 mm。全局及局部网格划分如图3所示，总网格数约为470万，网格质量大于85%。

图3 全局及局部网格划分

本文采用基于能量指数法的后验指数[15]来判断划分的网格是否足够用于LES计算。当求解的湍流动能达到总湍流动能的85%以上时，认为网格求解精度达到[15]。由于采用边界中心差分格式对动量方程进行离散，所以由数值格式引起的湍流动能耗散忽略不计。截面后检验指数M分布云图如图4所示，可以看出大部分区域后检验指数均大于85%，仅燃烧室下游中心局部区域解析不够，由于本研究集中在燃烧室头部出口的火焰区，所以可以认为该网格划分可满足本文研究要求。

图4 截面后检验指数M分布云图

1.1.4 数值模型

不可压大涡模拟的质量、动量和物质传输Favre滤波守恒方程如下：

(1)

(2)

先进行热态RANS计算以获得收敛场，而后激活LES计算。LES进行0.1 s物理时间后(10倍以上的流通时间)，在空气入口处施加激励，激励施加持续时间为0.25 s，期间同时采集数据。0.25 s的采集时间进行频域分析可获得频率分辨率为4 Hz。通过湍流火焰模型(TFC)计算湍流火焰速度[16-17]，该模型基于火焰团内小尺度湍流平衡假定，建立了湍流火焰速度与大尺度湍流参数关联，适用于工业预混系统中的褶皱火焰。甲烷燃烧采用GRI 3.0反应机理[18]。

1.2 火焰传递函数

火焰传递函数计算基于部分预混火焰是线性系统的假设。在线性时不变系统中，如果系统由弱激励信号激励，则可以识别系统的频率响应[19]。为了克服较短的LES仿真时间，采用离散随机二进制信号(DRBS)进行速度入口激励[5]。该辨识过程也被认为是Winer-Hopf方法，其优点是与扫频激励方法相比，单个LES仿真可以提供整个频带范围，激励幅值选为5%。图5为激励所用的离散随机二进制信号时域图。

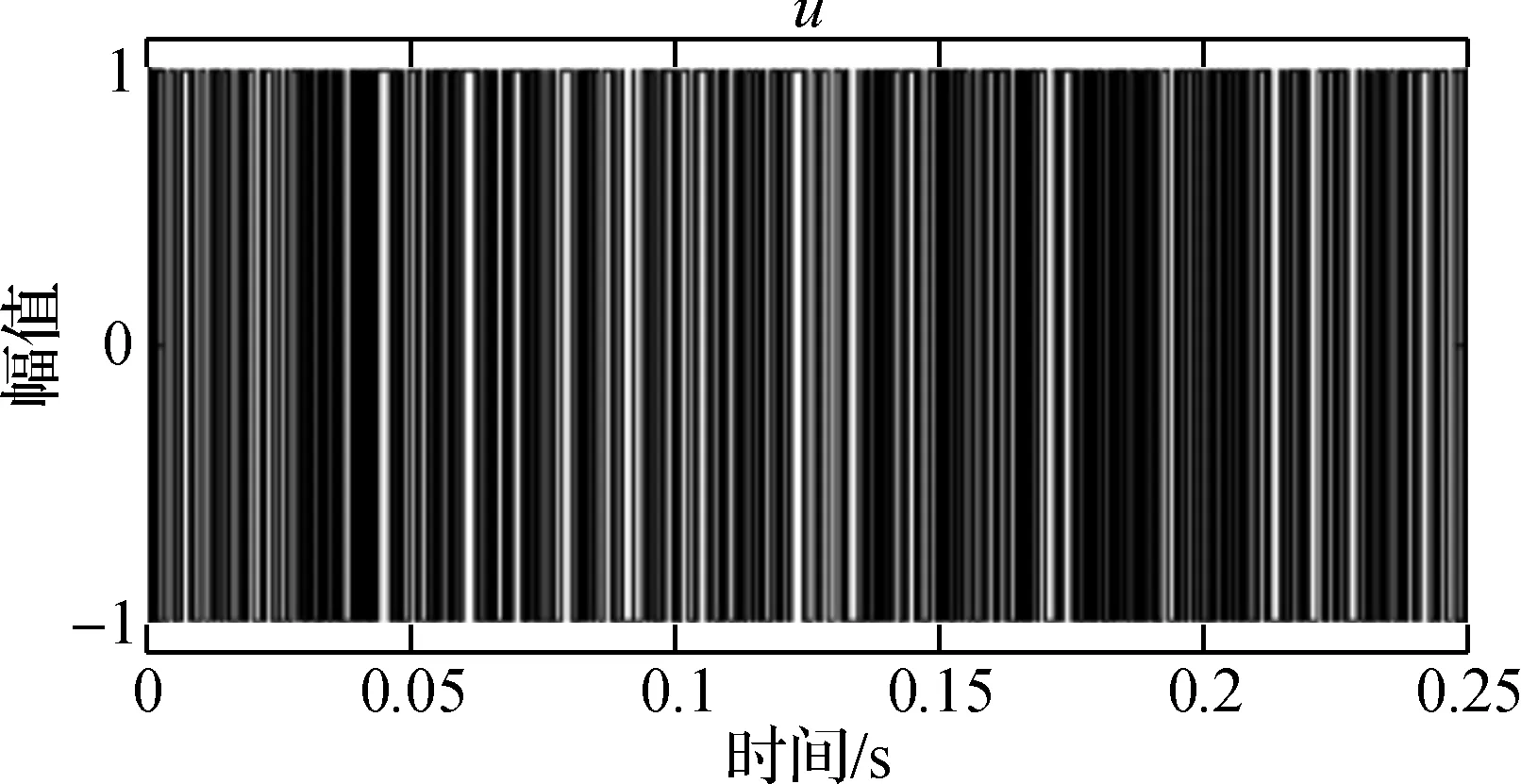
图5 离散随机二进制信号(DRBS)

方程(3)为火焰传递函数定义式:

(3)

图6 火焰传递函数计算步骤

2 结果与分析

2.1 燃烧场分析

上述16个DoE工况计算后的产物生成速率分布云图如图7所示，其中黑线表示轴向速度为零的等值线。由图7中轴向速度零等值线可知，在所有工况下燃烧室内部均可有效形成中心回流区和角回流区。形成的火焰结构可分为三部分：外层火焰、内层火焰和火焰前沿。外层火焰的根部显示出较高的放热速率，而内层火焰的根部为相反的结果。同时若火焰不一直沿径向传播，则中心回流区可能会变形。图7中，如工况6，12，13和15的产物生成速率轮廓所示，其火焰内层未锚定在中心体末端附近。所有工况中，火焰外层均维持在头部与燃烧室之间的连接点上。根据产物生成速率所展示的火焰形状轮廓，以上16种工况可划分为3种火焰类型，如表3所示。其中，A型火焰末端冲击到燃烧室外壳上，如工况1，4，7和8所示。C型火焰与中心回流区有强烈的相互作用，如工况6,12,13,15和16所示。B型火焰同时具有A型和C型火焰的复合特性，如工况2，3，5,9,10,11和14所示。

图7 各工况产物生成速率分布云图(黑线表示轴向速度为零的等值线)

表3 火焰类型划分

2.2 DoE分析

火焰形状与特定几何控制参数之间的关系可通过统计学中的方差分析(ANOVA)方法确定。表4列出了不同类型火焰的全因子回归模型所对应的p值，包括单个几何控制参数的p值和参数间相互作用关系p值。该表中还列出了各工况下燃烧室的总压损失，以综合考虑燃烧室气动压损特性。当p值小于0.01时，表明此几何参数对该类火焰形状有非常大的影响。由表4可知，对于A型火焰来说，没有明显的几何控制参数。对于C型火焰，最重要的几何控制参数为扩张角α，且较小的扩张角α将有利于C型火焰生成。B型火焰主要受扩张角α与燃烧室半径R4之间的相互作用影响，且中心体末端半径R1_TE和燃烧室半径R4也单独对该类火焰有作用关系。燃烧室总压损失大小主要受中心体末端半径R1_TE影响。总压损失随R1_TE的增加而增加，表明燃烧室总气动阻力增加。R1_TE的增加使得混合区整体流通截面积减小，导致混合区域流速增加，且压降与流速成正相关，因而流速增加后，压降得到升高。

表4 不同类型火焰全因子回归模型的p-value

总而言之，B型和C型火焰形成主要受扩张角α及其与燃烧室半径R4的相互作用控制。总压损失主要受中心体末端尺寸R1_TE控制。

2.3 火焰传递函数(FTF)分析

可以从LES结果采用上述的激励响应方法辨识反应火焰响应特性的火焰传递函数。该火焰传递函数可添加至低阶热声网络模型中或三维亥姆霍兹声学模型中预估燃烧系统的稳定性。火焰传递函数还可以扩展为弱非线性火焰描述函数，进而预测燃烧室热声极限环特性。燃烧室设计阶段也可单独分析火焰传递函数，通过FTF的增益来判断火焰是否有不稳定的风险，FTF的相位信息反应火焰的时滞。当增益高于1时，一般可认为火焰存在发生燃烧不稳定的高风险。

图8为16个工况下的火焰传递函数增益和相位信息。当频率高于400 Hz时，火焰传递函数增益小于1，火焰起低通滤波器的作用，火焰仅对低频有响应，而对高频响应不明显。某些工况下，在零频率附近具有较高的增益，而其它情况则显示较低的幅值。表5列出了增益大于1的频率带，如41 Hz、82 Hz、122 Hz和204 Hz。特别工况火焰传递函数增益存在明显的特征峰，如工况9的204 Hz、工况15的363 Hz及工况16的45 Hz。

表5 不同工况下特征频率带信息

图8 各工况火焰传递函数增益和相位

比较工况9和工况11，可以看出中心体后缘的直径(R1_TE/R1)和中心体末端到燃烧室前墙的距离(d)可能不会强烈影响参数该频段的火焰传递函数。比较工况3与工况11，表明燃烧室的半径R4对火焰响应频率特性影响不可忽略。比较图8火焰传递函数结果与表3中所示的火焰类别划分结果，可以看出两种结果之间没有太大的相关性。

总体来看，工况5，7和8只有一个响应频率带，且位于100 Hz以下；工况9，14和15也均只有一个频率响应带，位于200 Hz以上；其它工况响应频率带均有2个以上。在进行燃烧室和阻尼器的结构设计时，可结合火焰传递函数结果，优化设计结构与方案。