一种新型集成电驱系统的稳态温度场分析
2021-04-06邱明明秦菲菲
张 琰, 赵 韩, 黄 康, 邱明明, 秦菲菲
(1.中国计量大学 机电工程学院,浙江 杭州 310018; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)
本文研究的新型两挡变速一体化集成电驱系统集成度高、结构复杂,研究其温度场对于设计系统的润滑与冷却、优化结构参数以及提高系统的综合工作效率具有重要意义。
温度场计算的主流方法是采用集中参数热网络(lumped parameter thermal network,LPTN)方法和有限元方法(finite element method,FEM)。LPTN方法能够快速得到满足工程应用的温度分布,且计算量较小,其准确性取决于节点的划分和参数的选取;FEM方法精度较高,但是计算量较大,因此不适合在设计初期阶段应用。
关于电机和传动系统各自的温度场研究已充分开展。文献[1]提出了经典的同心圆柱体模型,同时考虑轴向热流和径向热流;文献[2]在同心圆柱体模型的基础上加以简化,提出了更实用的串联热阻模型;文献[3]用热网络方法分析了中小型感应电机的温度分布,重点研究了电机各部件间的热阻问题;文献[4]将热网络法概念引入机械传动系统的温度场计算中;文献[5]用热网络法计算了六挡位手动变速箱齿轮传动的动力损失;文献[6]用热网络法建立了高速重载船用齿轮箱关键部件的摩擦功耗及热阻计算模型,并利用Matlab求解。
在上述研究的基础上,本文分析了集成电驱系统的热源分布并建立热源模型;讨论系统内传热模式并建立热阻模型;采用LPTN方法建立系统的热网络模型,得到系统中关键节点温度,并利用试验方法对计算结果进行验证。
1 热网络法分析模型
1.1 热网络节点及热网络图
LPTN方法基于热电相似理论,参考电路模型建立热路模型。将温度类比为电压源,损耗类比为电流,各类热传递类比为电阻,热网络所遵循的规律亦与电网络相似。该方法应用图论理论完成系统热网络的拓扑结构绘制,编写热网络方程并完成相关参数计算代入求解。若热网络节点数过多,则热网络图复杂度提高,热平衡方程的计算量加大;若热网络节点数过少,则计算的准确度和精确度将会降低。
根据电机变速器一体化系统的结构分析其热传递路径,完成系统的热网络节点划分,结果如图1所示。根据划分的热网络节点分别绘制出电机变速器一体化系统各部分热网络图,以差速器部分为例,如图2所示。

图1 热网络节点
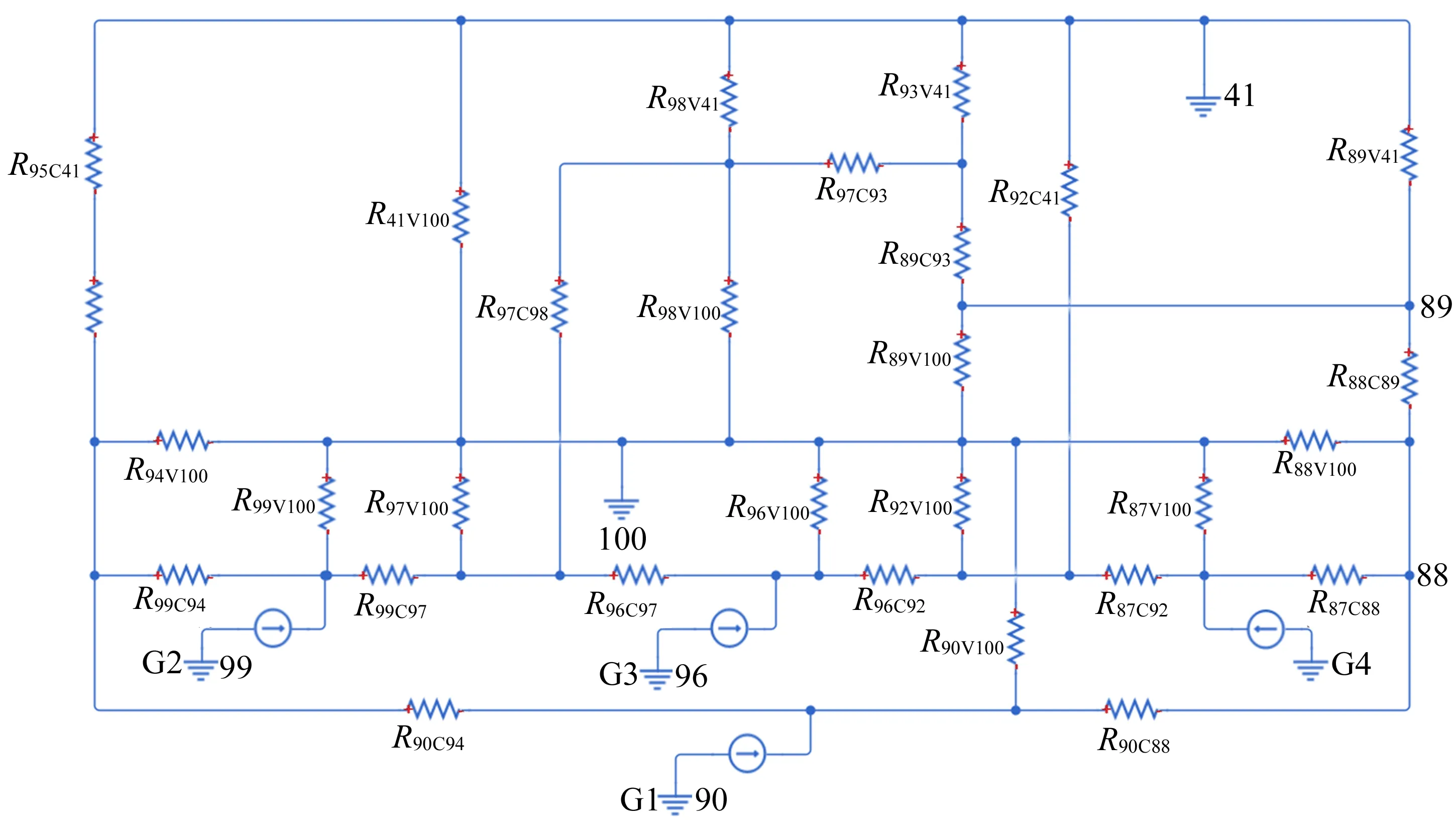
图2 差速器热网络
图1中:1~4为传动齿轮;O1~O8为轴承;1~86为节点编号。图2中:下标数字均为节点编号;下标字母区分热流性质,C表示热传导,V表示热对流。
1.2 系统热源分析
系统的热量来自于系统内部的功率损耗,包括电磁损耗和机械损耗2个部分。
1.2.1 电磁损耗
(1) 绕组铜损。转子绕组线圈通电产生铜损和附加损耗。其中由漏磁场、漏电流和集肤效应等引起的附加损耗数值上远小于基本铜损,故忽略不计。
根据焦耳楞次定律,绕组铜损为:
(1)
其中:IN为额定电流;Ra为绕组电阻。
(2) 铁芯铁损。电机的铁损来源于系统的交变磁场在转子铁心中产生的磁滞损耗和涡流损耗。磁滞损耗只取决于磁通密度的峰值,涡流损耗则受到磁通密度峰值及磁通密度变化率的双重影响。
齿部铁损为:
(2)

轭部铁损为:
(3)
其中:Gj为轭部铁心质量;Ka′为经验系数。
1.2.2 机械损耗
(1) 啮合摩擦损失。齿轮啮合摩擦主要考虑滑动摩擦,根据齿轮啮合原理和摩擦学理论,将斜齿圆柱齿轮等效为当量直齿圆柱齿轮计算功耗。齿面接触点的滑动摩擦功率为:
Pm=fvsFn
(4)
其中:f为滑动摩擦系数;Fn为齿轮法向载荷;vs为齿面相对滑动速度。
(2) 搅油损失。搅油损失是指由于润滑油的黏滞作用而产生的能耗。润滑油温度升高显著影响了润滑油的润滑能力和冷却效果。本文仅考虑在系统整体搅油损失中占比最大的齿轮搅油损失。
与齿轮侧面相关的搅油损失为:
(5)
与齿轮啮合面相关的搅油损失为:
(6)
其中:fg为浸油因子;υ0为运动黏度;D为分度圆直径;Ag为配置系数;Rf为粗糙度因子。
齿轮搅油损失为两者之和,即
PJ=Ps+Pn
(7)
(3) 风阻损失。风阻损失是指齿轮在箱体内的油气混合空间中旋转所产生的摩擦损失。根据文献[7]有:
(8)
其中:t为齿轮齿宽;R为齿轮节圆半径;ng为齿轮转速;ρ为流体密度;μ为流体黏度。
(4) 轴承功率损失。轴承滚动体与滚道的滑动摩擦损失产生的急剧温升会使零部件变形,减小工作游隙,甚至导致轴承抱死。轴承功率损失为:
H=Mω
(9)
其中:ω为轴承角速度;M为轴承摩擦力矩。
(5) 同步器功率损失。锁环式同步器的热量主要产生于同步换挡过程,同步环与待接合齿圈相互摩擦产生摩擦力矩,目标面和接触面热量由分配权重因子来分配。两接触表面由于摩擦产生的总热流功率损失[8]为:
q=ξT0vc
(10)
其中:ξ为能量换算因子;T0为等效摩擦应力;vc为相对滑动速度。
1.3 热阻模型建立
系统热源中一部分热量以热传导的方式传递给传动轴及箱体,一部分热量以热对流的方式传递给润滑油或油气混合物,再进一步传递给外界大气,最终达到热平衡状态。
1.3.1 导热热阻模型
箱体导热热阻模型可简化为一维平壁稳态导热热阻模型,平壁面积为A的导热热阻[9]为:
(11)
其中:δ为平壁的厚度;λ为材料的热导率。
转子、齿轮、轴承导热热阻模型可以视为圆筒壁的稳态导热热阻模型,长度为l的长圆筒的导热热阻为:
(12)
其中:r1为圆筒内径;r2为圆筒外径。
1.3.2 对流换热热阻模型
由于流体的黏滞作用,流体与物体表面的能量传递包含热传导和热对流2个部分:紧贴物体表面的流体处于静止状态,热量传递以热传导为主;而离开物体表面时,热量传递以热对流为主。对流换热系数无法直接测量得到,它反映对流换热强烈程度,通常可简化为管内强迫对流换热、纵掠平板对流换热、横掠单管对流换热和自然对流换热[10]4种问题进行讨论。
(1) 电机定转子气隙中的对流系数。电机变速器一体化系统是封闭式结构,定转子气隙中的空气随着转子的旋转做圆周运动,忽略轴向空气流动,定转子气隙的雷诺数为:
(13)
其中:v为转子外表面线速度;δ为气隙长度;ν为空气的运动黏度。
(2) 转子端面对流换热系数。绕组热量一部分通过定子传递到壳体,一部分通过电机转子套筒传递给机械部分,还有一部分通过转子端面散失到系统内部空气,再由内部空气通过壳体散失到外界。
转子端面的对流系数为:
(14)
(3) 轴承表面对流换热系数。轴承表面对流换热可简化为管内强迫对流换热问题。
层流状态(Ref≤2 300)时,换热系数为:
(15)
其中,η为流体的动力黏滞系数。
湍流状态(Ref>104)时,换热系数为:
(16)
过渡状态(Ref∈[2 300,10 000])时,换热系数为:
(17)
(4) 箱体表面对流换热系数。箱体表面对流换热可简化为流体纵掠平板对流换热问题。
层流状态(Rem≤5×105)时,换热系数为:
(18)
湍流状态(Rem>5×105)时,换热系数为:
(19)
过渡状态时,换热系数为:
(20)
(5) 齿轮和轴表面对流换热系数。齿轮和轴表面对流换热问题中的来流方向垂直于其发生对流换热的圆柱外表面,因此可以简化为横掠单管对流换热问题。表面对流换热系数为:
(21)
1.4 热平衡方程的建立
基于能量守恒原则创建系统热平衡方程组。以差速器部分为例,由图2可得热平衡方程组为:
(22)
同理可得集成电驱系统在各挡位时各部分的热平衡方程组。联立各个节点的稳态热平衡方程可得系统的热平衡方程为:
(23)
2 算例计算
系统处于低速挡时负载较大、工作效率较低、热功率损失较大、温升情况更严重,因此以一挡为例进行算例分析。传动系统选用永磁同步电机,电机参数如下:额定功率为36 kW;额定转速为400 r/min;额定转矩为86 N·m;额定电压为DC 326 V;一挡减速比为1.8。针对系统集成度高、安装空间狭小以及散热条件差的特点,在系统内部注入变压器油,起到润滑和冷却的双重作用,同时外部采用水冷方式冷却。已知空气平均温度实测为25.0 ℃,变速器侧润滑油平均温度实测为50.2 ℃。将初始温度、热源和热阻代入(23)式,采用Gauss消元法对系统热网络方程组进行求解,得到集成电驱系统内各节点的稳态温度值,如图3所示。

图3 LPTN各节点稳态温度
从图3可以看出:齿轮2的齿面温度(节点12)是系统稳态温度最高值,是该系统中的危险元件;除此以外,其他齿轮的齿面温度(节点32、节点36、节点78)也都在最高值附近,需要在后续齿轮强度校核和齿轮疲劳寿命计算时考虑温度影响。
3 温升试验
为验证温度场计算结果的有效性和准确性,依据三维建模设计进行了样机制作,如图4所示。
针对样机设计了温升试验。利用磁粉制动机作为电机变速器一体化系统的负载,绕组温度等内部温度可通过布置温度传感器(PT1000热敏电阻)测量,外部温度使用红外测温仪测量[10-11]。试验平台如图5所示。

图4 集成电驱系统样机

图5 样机温升试验平台
由升温试验测得的关键节点温度值与计算得到的LPTN值的对比见表1所列。从表1可以看出,试验结果与计算的LPTN值大致吻合。其中定子部分误差较大,这是由于简化热阻模型中铜损产热主要通过铁芯的热传导散热,但实际槽内结构复杂,有非均匀分布的漆包线和浸漆层,还有热传导系数较低的空气层和绝缘层导致的。
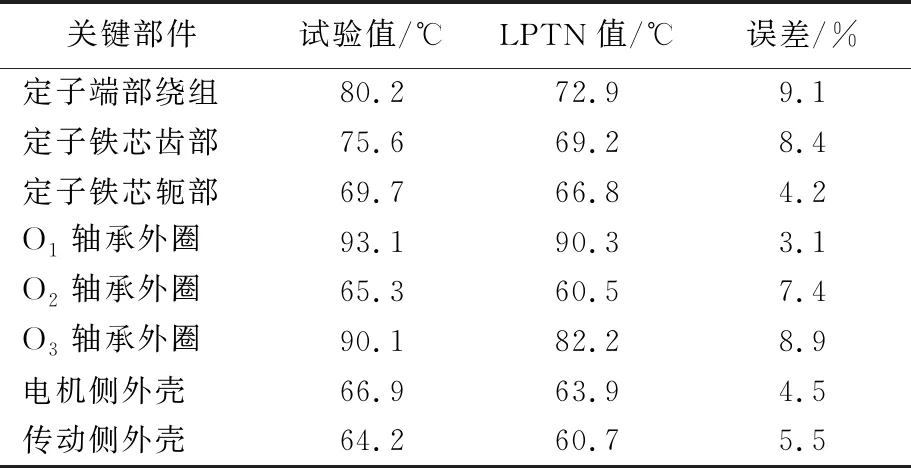
表1 关键节点温度的试验值与LPTN值的对比
4 结 论
本文针对一种新型集成动力系统,采用LPTN方法分析计算了系统的温度分布情况,并与试验测量数据进行对比,验证了本文方法的有效性和准确性,预测了高温部件位置,并分析了计算结果中较大误差产生的原因。热网络法计算量较小、计算速度快,适合前期设计预测应用,为后期该新型系统优化设计提供了基础。
