考虑顾客时间敏感的差异化排队策略

关银银, 李 凯,2

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

服务系统中长时间的等待和拥挤依旧十分常见,如快餐店用餐高峰期的排队点餐、车站排队买票取票以及快递站排队邮递包裹等。服务系统中的服务商主要通过降低成本或者直接提高收入以获得更大的市场竞争力。

近年来,很多学者研究了排队论中的成本问题。文献[1]基于排队论建立了比较模型来计算生产物流系统中的等待成本和资源成本以提高物流效率;文献[2]在最小化系统成本的目标下，研究了并行排队系统中最佳容量的确定以及灵活的技术选择问题。

考虑系统收入体现在如下2个方面:

(1) 服务商通过提高价格来增加收入。文献[3]研究了与需求无关的定价对M/M/1排队系统中收入优化的影响,或是通过改变服务率以服务更多数量的顾客从而提高系统收入;文献[4]开发了一种服务网络设计模型以最大化系统利润,服务网络中的每个设施分别被建模为决策变量不同的M/M/1排队模型和M/M/k排队模型。

(2) 规范顾客的排队行为。文献[5]研究表明，当系统队列长度超过系统的某个阈值时,禁止客户进入的策略可以最大限度地提高收入,同时对于线性和指数收入结构,提出了最优阈值的显式表达式。

为了提高顾客满意度,减少顾客等待时间,增加企业收益,服务系统需要针对不同需求的顾客提供差异化服务。例如，在银行,有一部分顾客可以在银行工作人员的指导下独自在机器上完成操作业务,而有一部分顾客则必须在柜台专业人员的操作下才能完成业务;在商店,有部分顾客选择私人订制的物品,而另一部分只需要统一规格的物品。为了应对顾客的个性化需求,服务系统的服务商面对双重选择：将这类差异化顾客视为普通顾客以节约服务成本,或是设置一个新的队列满足这类差异化顾客的需求以增加收益。在这类情形下,如何设置服务率以及在何种情况下设置就成了服务商不得不面对的问题。

本文运用比较的方法得出不同情形的优化结果。在排队论研究中,越来越多的学者研究多服务器多队列的排队系统,如文献[6-8]。文献[9]将具有免费和收费服务选项的双层排队系统建模为2个并行的M/M/1服务系统。本文考虑2个相互之间没有任何联系的排队系统之间的对比,为企业管理者提供一定的启发。

顾客在服务种类上可以分为一般顾客和特殊顾客,在时间要求上可以分为耐烦顾客和不耐烦顾客,其中不耐烦顾客对时间要求严格,在服务系统中的等待时间超过自己的容忍程度就会离开。文献[10-11]研究了具有不耐烦顾客的排队系统;文献[12]也研究了具有不耐烦顾客的排队系统,系统的服务器数量不确定,因为服务器数量的随机性会在系统中产生拥塞,所以该文重点研究了顾客的放弃行为以减轻系统成本。与这些文献不同的是,本文考虑为具有差异化需求的顾客额外设置一个队列,并在不同到达率情形下分别对比单队列双服务器和双队列双服务器的成本与收益,从而达到优化服务系统的目标。

单队列多服务器的服务系统在各方面明显优于多队列多服务器的服务系统,在这个前提下,本文假设为差异化顾客额外设置一个队列,并将含有这个特殊队列的服务系统与普通的单队列双服务器系统进行对比。本文首先考虑了排队系统中常见的泊松分布[13],其次考虑了梯形分布[14],并对比了系统成本与收益2种情况,得出在一定情况下设置差异化队列对服务系统和顾客是双赢的结论。在梯形到达模型中,本文还考虑不耐烦顾客,通过对比可以了解到服务商单独设置差异化队列的优势。

1 标准排队系统

1.1 基本假设

本文考虑2个服务系统模型的比较,这2个模型分别为单队列模型和双队列模型,如图1所示。

图1 单队列模型和双队列模型

在单队列模型中,服务系统中有2台服务器,但顾客只能按照一个队列接受服务,到达率为λ,每个服务器都只能进行普通服务,2台服务器的服务率均为μ。

在双队列模型中,服务系统中有2台服务器,但顾客有2个队列进行选择,其中一个队列既可以进行普通服务,又可以进行个性化服务。如银行的窗口服务既可以进行简单的存取款业务,又可以针对不同顾客需求进行特殊的业务;服装定制店的设计师既可以制作统一样式的衣服,也可以为顾客量身定做符合其个性化需求的服装。即在排队系统中,处理复杂任务的服务器也可以进行简单的任务处理，本文称此队列为特殊队列,服务此类顾客的服务器为特殊服务器；另一个队列的顾客只能进行普通服务,本文称为普通服务器。2个队列的到达率分别为λ1和λ2,且λ1+λ2=λ,2台服务器的服务率分别为μ1和μ2。

本文首先考虑标准排队模型：① 在单队列模型中,2台服务器的服务时间分布均为指数分布,服务率均为μ,顾客到达时间间隔服从指数分布,顾客到达过程为泊松分布,到达率为λ；② 在双队列模型中,2台服务器的服务时间分布均为指数分布,服务率分别为μ1、μ2,本文假设μ2=μ′,顾客到达时间间隔服从指数分布,顾客到达过程为泊松分布,到达率分别为λ1、λ2,且λ1+λ2=λ。

1.2 优化结果分析

从系统整体角度来说,随机服务系统的单位成本不仅包括服务器的运营成本,还包括顾客的等待成本,单位时间全部成本的期望值为:

Z=c1m+c2Ls

(1)

其中:m为服务器数量;c1为每个服务器单位时间的成本;c2为每个顾客在系统停留单位时间的成本,即等待成本;Ls为系统中顾客平均数。假设双队列模型中2台服务器不存在任何差异,则单队列模型的单位成本为Z1=2c1+c2Ls,双队列模型的单位成本为Z2=2c1+c2(Ls1+Ls2)。

若单队列模型为M/M/2,双队列模型为相同的2个M/M/1,则单队列模型优于双队列模型。显然,服务商在面对此种情形时都会选择单队列模型,即当2个服务系统分别为标准的M/M/2系统和2个相同的M/M/1系统时,从单位时间全部成本角度出发,单队列模型M/M/2系统的单位成本明显小于双队列模型2个相同的M/M/1系统,服务商会选择M/M/2系统。但是,当系统中出现一类特殊顾客时,此类顾客的服务是差异化的,服务商面对这种需要个性化服务的顾客时,在不同条件下应该选择不同的服务模型,服务商可以将其视为普通顾客选择单队列模型，也可以设置特殊队列选择双队列模型。服务商设置特殊服务器以服务差异化顾客会产生不同的成本,此时服务商就要在设置特殊服务器产生的额外成本与不设置特殊服务器丧失的部分顾客之间取得平衡。

定理1 单队列模型为标准的M/M/2系统,双队列模型为2个不同的M/M/1系统,当2种模型单位成本相同时,令双队列模型中特殊服务器的服务率为μ′*,有如下情况:

(1) 若双队列模型的服务率均为μ,每个服务器单位时间的成本均为c1时,无论双队列模型中2个队列的到达率如何分布,则单队列模型都优于双队列模型。

(2) 若双队列模型的服务率分别为μ、μ′,到达率均为λ/2,每个服务器单位时间的成本均为c1,则μ′*=λ+μ。

(3) 若双队列模型的服务率分别为μ、μ′,到达率分别为λ1、λ2,且λ1+λ2=λ,每个服务器单位时间的成本为c1、c1′,则μ′*为:

(2)

(3)

当μ′>μ′*时,选择双队列模型;当μ′=μ′*时,2个模型均可;当μ′<μ′*时,选择单队列模型。

证明在此只给出情况(1)的证明过程,情况(2)、情况(3)类似。

在单队列模型中,Ls=4λμ/(4μ2-λ2),在双队列模型中,2个M/M/1系统中顾客的平均数为:

2个成本函数的差可以定义为关于到达率λ1的二次函数,即f(λ1)=Z1-Z2=c2(Ls-Ls1-Ls2),且

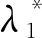
单位时间全部成本的期望值是从系统整体角度出发,既考虑服务系统中服务器的运行成本,又考虑顾客的等待成本,本文在考虑系统成本的基础上,进一步研究了从服务商角度出发的服务系统收入优化问题。在标准排队系统中,若不考虑顾客的等待成本,则服务商单位收益的均值可表示为:

π=pλ-cμ

(4)

其中:p为服务系统服务单位顾客的收入;c为服务器运行的单位成本;λ为服务系统中顾客的到达率;μ为服务系统中服务器的服务率。

在双队列模型中,若2个服务器的服务率均为μ,服务单位顾客的收入均为p,服务器运行的单位成本均为c,无论顾客的到达率如何分布,则服务商的选择不同于定理1中的情况(1),单队列模型和双队列模型的收益都是一样的。若双队列模型中2个服务器的服务率不同,分别为μ、μ′,到达率均为λ/2,服务单位顾客的收入均为p,服务单位顾客的成本均为c,则当μ′>μ时,服务商应选择单队列模型；当μ′<μ时,服务商应选择双队列模型。若双队列模型中2个服务器的服务率不同,分别为μ、μ′,2个队列的到达率分别为λ1、λ2,且λ1+λ2=λ,服务单位顾客的收入为p、p′,服务器运行的单位成本为c、c′,则服务商会面对不同的选择。

定理2 单队列模型为标准的M/M/2系统,双队列模型为2个不同的M/M/1系统,从服务商单位收益的角度出发,当双队列模型中服务单位顾客的收入为p、p′,服务单位顾客的成本为c、c′,有如下情况:

(1) 若双队列模型的服务率均为μ时,则双队列模型中使得2个模型的单位收益相等的第1个到达率为：

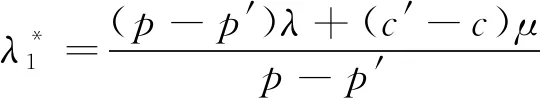
(5)

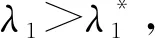
(2) 若双队列模型的服务率分别为μ、μ′,则到达率分别为λ1、λ2,且λ1+λ2=λ,每个服务器单位时间的成本分别为c、c′。① 若cμ≤(p-p′)×(λ-λ1),则单队列模型收益恒大于双队列模型;② 若cμ>(p-p′)(λ-λ1),则双队列模型中使得2个模型的单位收益相等的第2个服务率为:

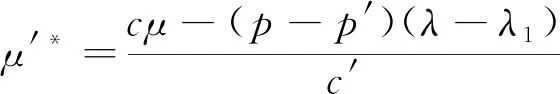
(6)

当μ′>μ′*时,选择单队列模型;当μ′=μ′*时,2个模型均可;当0<μ′<μ′*时,选择双队列模型。

通过比较服务商单位收益与服务系统单位成本的优化结果可以发现,是否考虑顾客的等待成本,对服务商的决策会产生不同的影响。从服务商收益角度出发,当双队列模型中提供差异化服务时,若提供普通服务的服务器的运营成本比较大时,服务商可以设置较小的服务率以提高企业收益；若提供普通服务的服务器的运营成本非常小时,单队列模型总是优于双队列模型。在现实生活中,顾客的等待成本难以准确衡量,主要原因是顾客的单位等待成本不同,顾客对时间的敏感程度有所差异,因此,本文还考虑了不耐烦顾客,为了便于计算,本文假设顾客对时间的敏感程度是一样的。

1.3 算例分析

某服装定制店既可以按照顾客需求定做服装,也可以为无特殊需求的顾客提供统一样式的服装。假设顾客的平均需求量为每周5套,服装店共有2位服装设计师可以完成顾客需求,且每位服装设计师平均每周可以完成4套服装,即λ=5,μ=4。

(1) 根据单位时间全部成本的期望值,单队列模型的顾客平均数为Ls≈2.05。对于双队列模型，下面分不同情况具体分析。① 双队列模型中μ1=μ2=4,当λ1=3,λ2=2时,Z1=2c1+2.05c2,Z2=2c1+4c2,单队列模型优于双队列模型。② 双队列模型中λ1=λ2=1/2λ,μ1=μ=4,μ′*=9,若μ2=μ′=8,Z1=2c1+2.05c2,Z2≈2c1+2.12c2,则单队列模型优于双队列模型;若μ2=μ′=10,Z1=2c1+2.05c2,Z2=2c1+2c2,则双队列模型优于单队列模型。③ 双队列模型中λ1+λ2=λ,μ1=μ=4,为方便计算，此时假设c1=4,c1′=2,c2=1,λ1=3,则μ′*≈3.90,当μ2=μ′=3时,Z1=10.05,Z2=11,单队列模型优于双队列模型;当μ2=μ′=4时,Z1=10.05,Z2=10,双队列模型优于单队列模型。

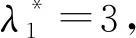
2 梯形到达排队系统

2.1 基本假设

在梯形到达排队系统中,考虑顾客是不耐烦的,随着队列长度的增加,顾客会选择性加入队列,在可以容忍的范围内加入,在超过可以容忍的长度时选择离开。面对不耐烦顾客,服务商设置的服务率大小对服务系统的收益至关重要,在这个系统中本文主要从服务商的角度出发,在不考虑顾客的等待成本情况下,针对不同类型的顾客设置不同的服务率从而最大化收益,假设服务系统服务单位顾客的收入为p,服务单位顾客的成本为c,服务的顾客总数为n,服务商的总收益为V,则

V=n(p-c)

(7)

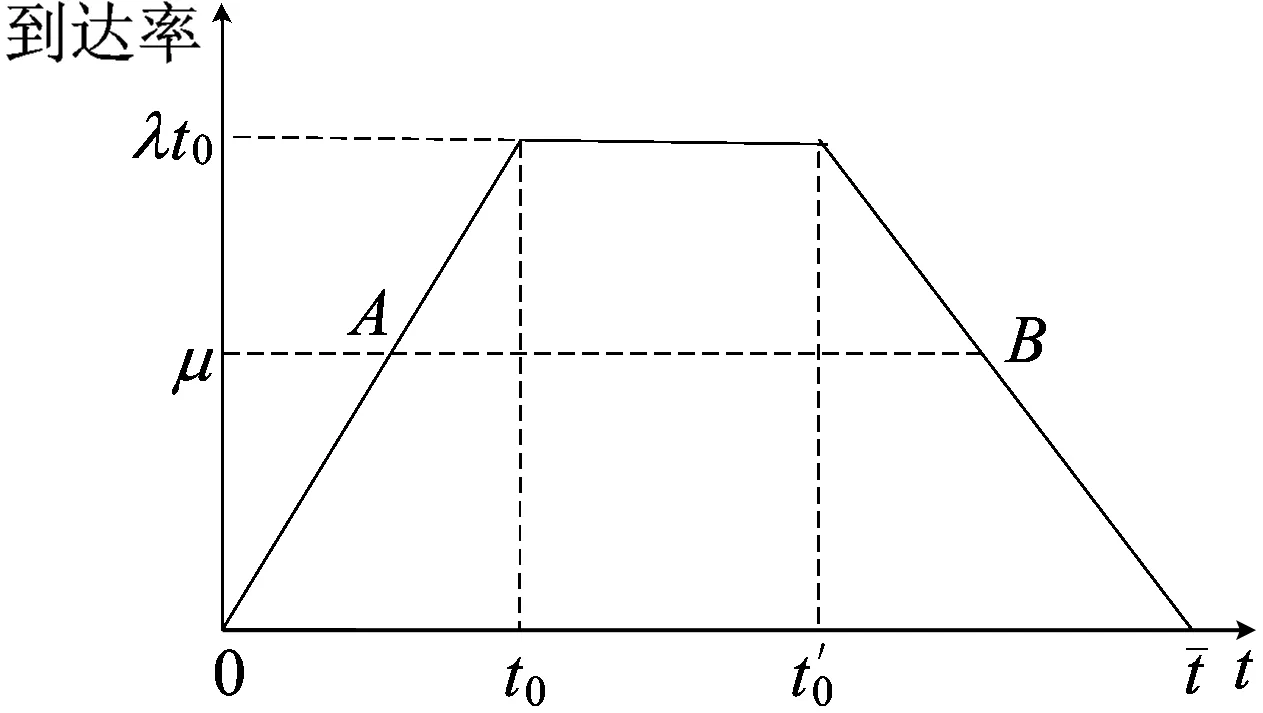
图2 梯形到达过程

在单队列模型中,2台服务器的服务率均为μ,顾客的到达率为Λ(t)。

在双队列模型中,2台服务器的服务率分别为μ、μ′,顾客到达率分别为Λ1(t)、Λ2(t),并且其中λ1+λ2=λ。

2.2 优化结果分析

在单队列模型中,2台服务器的服务率均为

(8)

在0～t0时间段内,根据顾客到达率可以计算出进入服务系统的顾客总数为：

(9)

服务系统积累的最大队长假设为Qμ,根据服务率与到达率的交点可以计算出最大队长为:

(10)

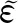
(11)

Q2μ=

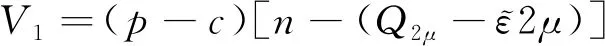
(12)

在双队列模型中,2台服务器的服务率分别为μ1、μ2,顾客到达率分别为Λ1(t)、Λ2(t),即

(13)

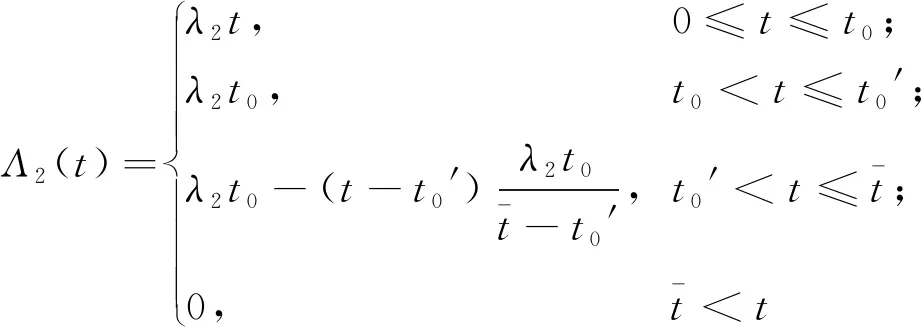
(14)

(15)

(16)

由于其中一个队列既可以进行普通服务,又可以进行个性化服务,服务此类顾客的单位收入和单位成本都不同于只能进行普通服务的队列,服务单位顾客的收入为p′,服务单位顾客的成本为c′,服务系统中服务商的总收益为:

(17)

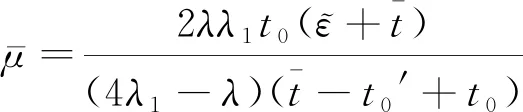
(18)

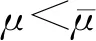
(19)

当μ′在(μ1′*,μ2′*)范围内时,双队列模型优于单队列模型,服务商面对此类情况应该选择双队列模型,当μ′不在(μ1′*,μ2′*)范围内时，服务商应该选择单队列模型。

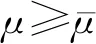
实际情况中,若存在系统中积累的最大队长小于顾客所能容忍的最大队长,则系统中所有的顾客都可以被服务,此时情况比较复杂,本文仅详细考虑系统中积累的最大队长大于顾客所能容忍最大队长的情况。

比较单队列模型和双队列模型,令f(μ′)=V1-V2,进行2次求导即可得出上述结果。

从上面的研究结果可以看出,服务商面对需要个性化服务的顾客时,如果要设置足够大的服务率才能满足顾客的需求,那么双队列模型对服务商来说不是一个好的选择；如果服务商不需要设置很大的服务率就能满足顾客的差异化需求,那么双队列模型对服务商来说是个更优的选择。具体来说,当双队列模型中普通队列的到达率明显小于特殊队列时,特殊服务器服务单位顾客的收入与成本之差明显大于普通服务器服务单位顾客的收入与成本之差时,服务商只有当特殊服务器的服务率在一定范围内时才会采用双队列模型;当双队列模型中普通队列的到达率不那么小时,普通服务器的服务率在特定范围内或者超过特定范围时,服务商都是当特殊服务器的服务率在比较小的时候选择双队列模型。

2.3 算例分析

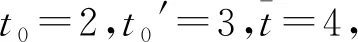
(1) 假设μ1=μ=3,此时单队列模型中服务商的总收益V1=62.82,进一步可以计算出A≈0.78,(p′-c′)/(p-c)=4/3,根据求根公式求解可得μ1′*≈2.08、μ2′*≈9.62,当μ2=μ′=3时,双队列模型中服务商的总收益V2=71.94,此时双队列模型更优。

(2) 假设μ1=μ=13,此时服务率远远大于到达率,单队列模型中所有顾客都可以被服务,服务商的总收益V1=75。① 若μ2=μ′=5>4,则双队列模型中所有顾客均可被服务,服务商的总收益V2=85,双队列模型优于单队列模型;② 若μ2=μ′=2.5<4,则双队列模型中服务商的总收益为V2≈79.53,双队列模型更优。

3 结 论

本文分别研究了标准排队系统下和梯形到达排队系统下单队列模型和双队列模型的对比,在标准排队系统中,顾客到达时间间隔服从指数分布,顾客到达过程为泊松分布,系统中服务器的服务时间分布均为指数分布,以系统整体的单位时间成本和收益为目标比较这2个系统的性能,即典型的M/M/2和2个M/M/1之间的比较;而在梯形到达排队系统中,顾客的到达过程假设为先上升；上升至最高点后维持一段时间、然后下降的梯形,并考虑顾客是时间敏感的,系统中队列长度超过最大容忍程度则会离开,通过比较单队列双服务器和双队列双服务器2个系统，分析了服务商面对差异化顾客群体在不同的情形下应该设置不同的服务率以获取更高的收益。

从随机服务系统角度出发,系统各项性能指标都是影响系统优良的关键,本文在标准排队模型中主要考虑了系统中的平均顾客数,顾客在系统中的平均逗留时间、单位顾客在系统中的等待时间等都是未来可以研究的方向。此外,本文在梯形到达模型中考虑了不耐烦顾客、队列长度和服务器的服务率对顾客都是可预见的,顾客根据预估的等待时间和服务率大小判断是否继续等待,从系统角度出发优化服务提供商的收益大小。未来可以考虑系统中积累的最大队长小于顾客所能容忍最大队长的情况,也可以从顾客角度出发,优化顾客在系统中的等待时间,进一步提高顾客满意度,增加社会效益。