龙卷风作用下四坡屋面建筑风荷载特性数值模拟研究

王 辉, 吴洁颖, 李 娜, 袁海东, 陈杰生, 吴润华

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640)

龙卷风是一种地区性小尺度大气涡旋,突发性强,生消迅速,出现时风雨交加,破坏力极大[1]。美国是龙卷风频发的国家,素有“龙卷风之乡”之称,该国每年因龙卷风灾害而造成的经济损失和人员伤亡巨大。我国龙卷风多发生在沿海城镇地区,龙卷风一旦出现,必将给当地房屋造成严重破坏,带来巨大生命财产损失,而对于房屋建筑的抗龙卷风设计,我国现行有关规范还缺乏必要的设计指导条款。

目前,国内外关于龙卷风的研究主要采用现场实测、龙卷风装置试验以及数值模拟的方法。现场实测最为直接,但其开展起来较困难,耗资大且具有一定的危险性,且龙卷风生消迅速,难以捕捉。数值模拟能较直观地获取近地风场特性,通过参数变化形成不同等级和不同结构的龙卷风场,随着计算流体动力学(computational fluid dynamics, CFD)理论以及计算硬件的发展,数值模拟已成为研究龙卷风的主要方法之一[2]。

国内外研究者采用数值模拟和模型试验方法,对龙卷风作用下的低矮建筑开展了一些研究[3-7],其对象主要针对平屋面和双坡屋面建筑,关于屋面形式变化以及细部构造对建筑风荷载影响的研究很少。四坡屋面是一种较典型的建筑外形,目前对该类型建筑的风荷载研究主要针对良态风,如何设计提高该类建筑抵抗龙卷风作用的能力,是目前风工程重点关注的研究课题。基于改进的龙卷风模型,本文采用CFD数值模拟方法,对龙卷风作用下的四坡屋面低矮建筑风荷载开展研究;考虑不同龙卷风方位角,选取5种屋面坡角建筑进行模拟,重点研究屋面坡角以及有、无挑檐对建筑屋面风压分布的影响,分析获取屋面风压分布特性及影响规律。

1 龙卷风风场的数值模拟

采用Rankine涡模型[8]表示龙卷风切向风速分布。Rankine涡不考虑轴向流运动的二维涡,模型简单且有精确解,能反映龙卷风水平面流场的一般性规律。Rankine涡模型的风速计算公式为:

(1)

其中:vt为切向风速;r为风场中某点距风场中心距离;Rmax为核心半径(最大切向风速对应的半径);vmax为最大切向风速。

1.1 湍流模型及控制方程

采用具有广泛应用性的剪切应力传输(shear stress transport,SST)k-ω湍流模型[9],该模型由于在湍流黏度定义中考虑了湍流剪切应力的输运过程,可以用于带逆压梯度的流动和旋流流动计算。湍动能k与耗散率ω方程如下:

Gk-Yk+Sk

(2)

Gω-Yω+Dω+Sω

(3)

其中:ρ为空气密度,ρ=1.225 kg/m3;Gk、Gω分别为k、ω产生的平均速度梯度;Γk、Γω分别为k、ω的有效扩散项;Yk、Yω分别为k、ω的发散项;Dω为正交发散项;Sk、Sω为用户自定义源项。

1.2 风场模型及边界条件

基于文献[10]模型装置原理,通过尺寸改进建立龙卷风风场模型,风场模型及网格划分示意图如图1所示。图1a中,底部入流区与上部对流区的半径R均为400 mm,其中入流区高度h0=400 mm,对流区高度H0=1 600 mm。采用自适应较好的四面体非结构化网格对计算区域进行划分,由于主要研究近地面龙卷风对建筑的作用,因此对近地面网格进行加密,最小网格尺寸为0.004 m,最终划分网格数约为70×104。边界条件设置:入流面为速度入口(velocity inlet),径向风速和切向风速设定为0.5 m/s,出流面为压力出口(pressure outlet),而壁面(wall)设置为静止壁面,考虑壁面附近流体变化复杂,采用近壁模型法[11]进行处理。根据文献[12],龙卷风流场主要受涡流比S、径向雷诺数Re、高宽比a3个参数控制,模拟时S=0.5,Re=1.38×104。3个参数计算公式为:

(4)

(5)

(6)

其中:h0为入流高度;R为上升气流半径;v0为R处的切向速度;u0为R处的径向速度;β为入流风角度;ν为空气运动黏性系数,ν=1.45×10-5m2/s。

1.3 模型计算分析验证

对无建筑的龙卷风风场进行模拟,通过分析比较无量纲化后的切向速度验证模拟的准确性。30 mm高度处的切向风速云图如图2所示。30、50 mm高度处切向风速沿径向的分布及Rankine涡模型计算结果如图3所示。图3中,z为指定高度。由图2可知,在涡中心处,切向风速接近于0,沿半径方向远离涡中心后,切向风速迅速增大,在核心半径处切向风速达到最大值,核心半径以外,切向风速随半径的增大又缓慢减小,符合龙卷风风速分布特征。从图3可以看出,切向速度分布与Rankine涡模型的结果吻合较好,从而验证了模拟方法具有较高准确性。

2 模拟结果与分析

2.1 屋面坡角对屋面风压分布影响

四坡屋面建筑模型如图4所示,按1∶1 000缩尺建模,由于本文研究对象为普通低层建筑,结构刚性较大,不考虑建筑与风场之间的耦合作用,故采用刚性模型。该建筑长度L=24 mm,宽度W=16 mm,高度H=4 mm,屋面坡角α分别为15.0°、22.5°、30.0°、37.5°、45.0°,为便于分析,将屋面划分A、B、C、D 4个区,如图5所示。图5中,方位角θ定义为龙卷风中心的连线与结构长轴方向的夹角,选取0°、45°、90°龙卷风方位角,研究屋面α变化对屋面风压分布的影响(由于为封闭建筑,仅考虑建筑外表面风压)。0°方位角下,B区、C区为迎风屋面;45°方位角下,B区为迎风屋面;90°方位角下,A区、B区为迎风屋面。根据文献[12]的研究,当结构处于龙卷风核心半径处时整体所受风压较大,故模拟时不再考虑建筑的径向位置变化,所有工况的建筑都位于建筑高度所对应的核心半径处,本文龙卷风风场核心半径Rmax约为90 mm。

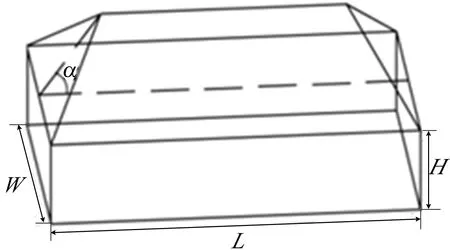
图4 四坡屋面建筑模型

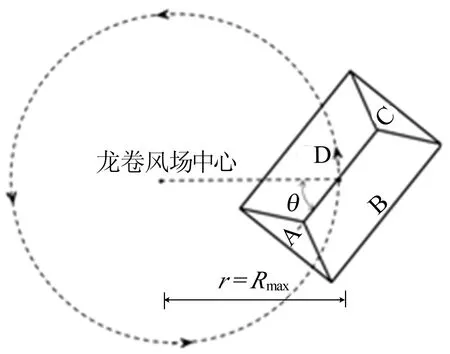
图5 屋面分区及方位角示意图

为描述建筑表面风压,引入无量纲化的风压系数CP,定义为:

(7)

其中:P为测点风压;Pref为参考点静压,本文取标准大气压。

2.1.1 屋面风压分布

0°方位角下不同坡角屋面风压系数分布云图如图6所示。由图6可知,对于各坡角的建筑屋面,迎风屋面B区、C区靠近檐口的端部区域CP呈正值,即屋面风荷载作用形式为风压力,正压最大值出现在迎风前檐区域,远离来流的位置,正压量值不断减小并逐渐向负压过渡。背风屋面A区、D区CP均为负值,荷载作用形式为风吸力,在靠近屋脊区域出现较大负压。

当α=15.0°时,屋面整体CP主要表现为负值,仅在B区、C区靠近檐口的端部区域CP出现正值,除A区、B区相交的斜脊线区域负压值较大外,其余表面CP绝对值较小且分布均匀。负压最大值出现在A区、B区斜脊线的檐口位置,随坡角增大,负压较大的区域逐渐靠近屋面中心,并向C区、D区交接的脊线(斜脊线)扩展。当α为30.0°、37.5°时,负压最大值均接近-1.1,且α=30.0°时最大值位于正屋脊线上方,α=37.5°时负压最大值位于D区靠近斜脊线区域。

当α进一步增大时,迎风屋面B区、C区整体正压量值明显增大,且正压的作用范围也随之增大,迎风屋面B区、C区风压逐渐由负压变为正压,当α=45.0°时,迎风屋面B区大部分呈正压状态;随着α增大,背风屋面A区、D区整体风吸力量值也显著增大,其中D区负压最大值首先出现在靠近屋面中心处;随着α增大,负压最大值沿着斜脊线逐渐向D区右上角移动,其CP最大值变化范围为-0.5 ～-1.1,A区的变化范围为-0.8 ～-0.9。当α=45.0°时,背风屋面D区整体承受较大的风吸力。

0°方位角下2个不同坡角屋面水平和竖直中心剖面位置的风迹线如图7、图8所示。从图7可以看出,气流在模型背风屋面出现明显的流动分离和漩涡,这也是导致背风屋面负压较大的原因。从图8可以看出,α增大加强了气流在屋脊处的流动分离,在屋脊背风屋面形成漩涡,产生较大的逆压梯度,随着α增加,漩涡范围和中心高度有所增加导致背风屋面负压区增大。

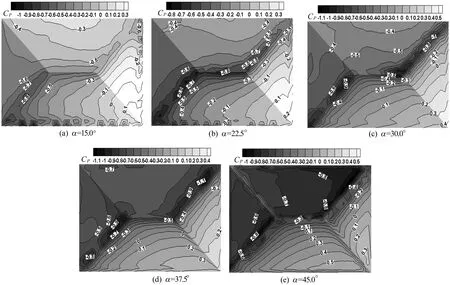
图6 0°方位角下不同坡角屋面CP云图

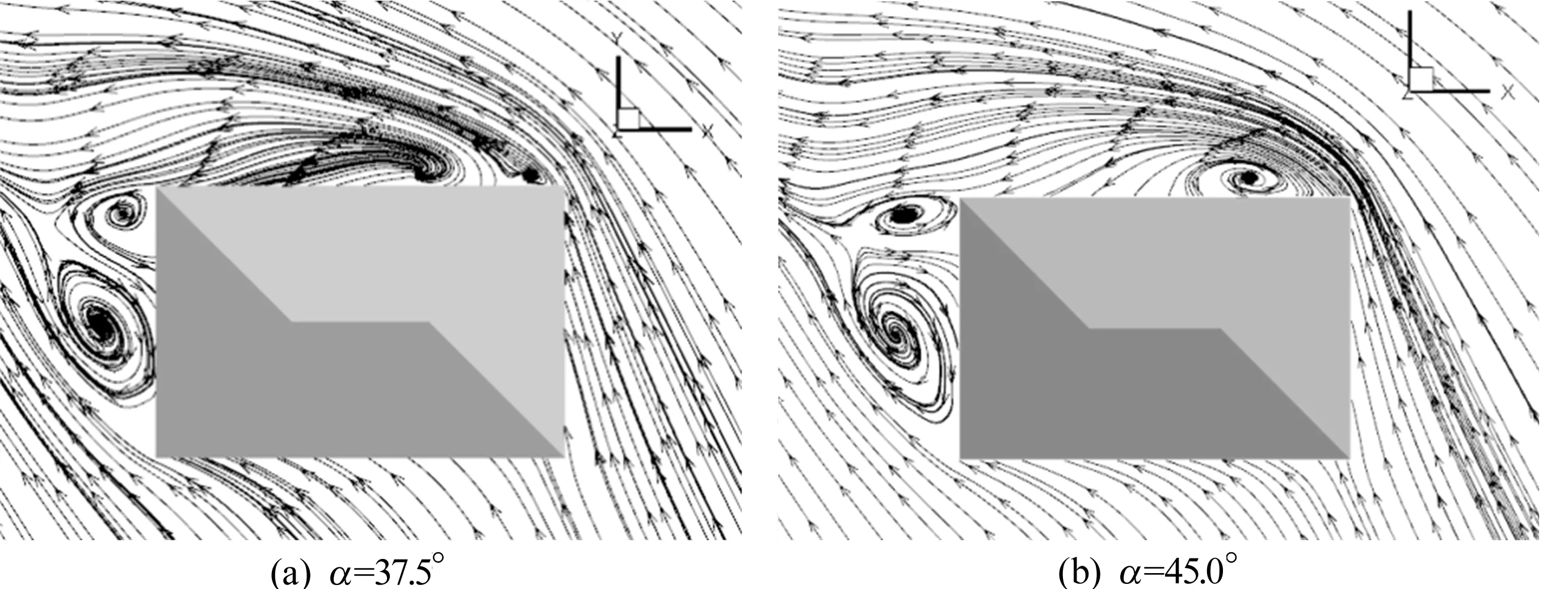
图7 0°方位角下z=4 mm处不同坡角建筑水平剖面位置风迹线

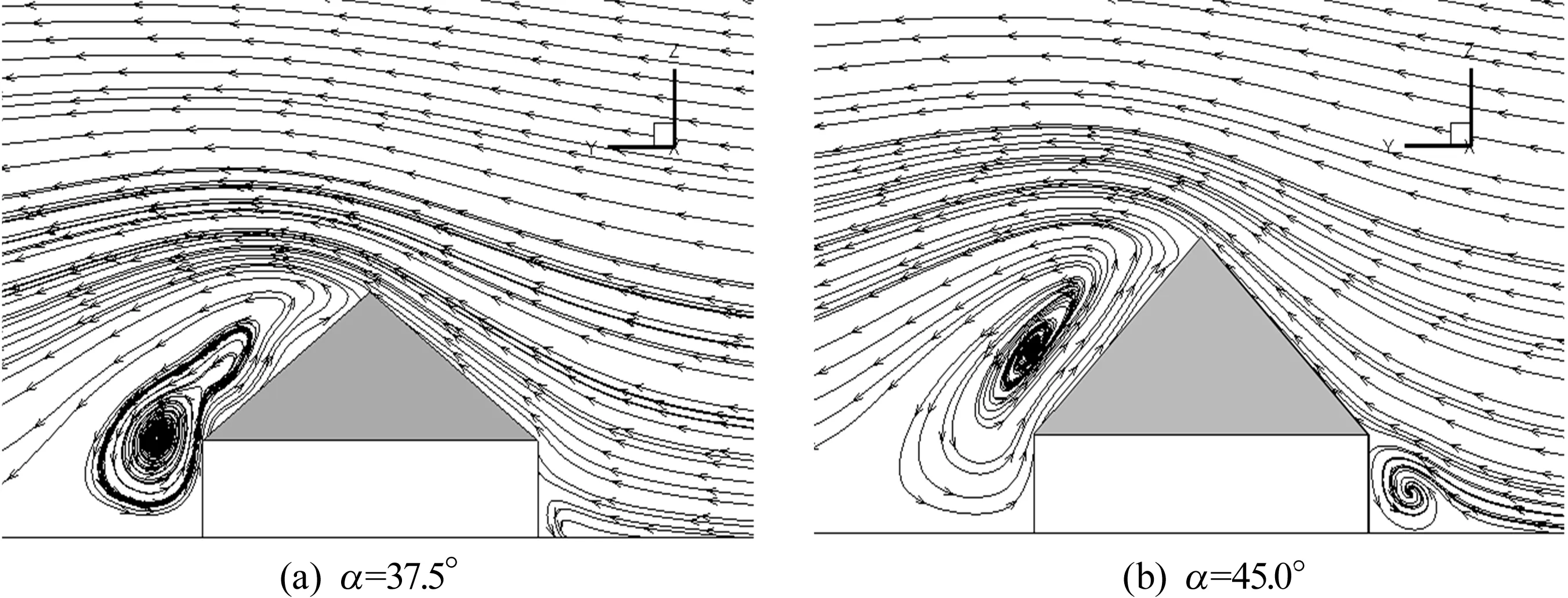
图8 0°方位角下不同坡角建筑竖直中心剖面位置风迹线分布

0°方位角下不同坡角屋面周边涡量分布如图9所示。从图9可以看出,α=37.5°时屋面在迎风A区和背风D区靠近屋脊线附近出现漩涡脱落现象,α=45.0°屋面在迎风A区和背风D区出现大量漩涡45.0°方位角下不同坡角建筑屋面CP云图如图10所示。45.0°方位角下,屋盖表面风压大致沿屋盖短轴对称分布,在α为15.0°、22.5°时,屋盖表面几乎全部为负压,背风屋面靠近屋脊线区域负压值较大,其余表面CP绝对值较小且分布均匀。随着α增加,迎风屋面B区正压区域不断扩展且量值显著增大,A区、C区、D区负压值也不断增大,负压最大值从正屋脊线上方移动到靠近B区斜脊线区域。

90°方位角下不同坡角建筑屋面CP云图如图11所示。由图11可知,90°方位角下,当α=15.0°时,屋面整体CP主要表现为负值,仅在A区、B区相交的斜脊线区域两侧CP出现较小正值。当坡角α为30.0°、37.5°、45.0°时,背风屋面负压值明显增大,最大值出现在A区、D区相交的斜脊线区域,且A区、B区正压分布区域随α增大而增大。

总体分析可知,对于各龙卷风方位角,当屋面α较小时,迎风屋面大部分受负压作用,随着α增大,迎风屋面分区风压逐渐由负压变为正压,正压作用范围不断扩大,当α=45.0°时,迎风屋面分区大部分呈正压状态;背风屋面始终受风吸力作用,随着α增大,背风屋面分区整体风吸力量值显著增大,负压最大值主要沿着屋脊线逐渐移动扩展。当α=45.0°时,背风屋面分区整体承受较大的风吸力。

图9 0°方位角下不同坡角建筑屋面周边涡量分布

图10 45°方位角下不同坡角建筑屋面CP云图

图11 90°方位角下不同坡角建筑屋面CP云图

2.1.2 屋面风载体型系数

区域风荷载体型系数μs为:

(8)

其中:CPi为测点i处的风压系数;Ai为测点i所属面积。

各方位角下屋面分区μs随坡角变化如图12所示。

由图12可知:

(1) 0°方位角时。迎风屋面B区、C区在α为15.0°～ 37.5°范围内,μs表现为负值,其绝对值随α增加而减小,随着α继续增大,C区μs发生明显转折,并由负值转变为正值,B区μs则反向偏转向较大负值发展;背风屋面A区、D区μs始终表现为负值,随着α增加,μs绝对值不断增大,其中D区系数在α=37.5°时发生转折,绝对值有所减小。

(2) 45°方位角时。B区迎风屋面μs在α为15.0°～30.0°范围内表现为负值,其绝对值随α增大而减小,随着α继续增大,μs过渡为正值,并随α增大而增大;背风屋面A区、C区、D区μs在各α范围内始终表现为负值,其中C区μs绝对值随α增加而增大,而A区、D区μs变化幅度较小。

(3) 90°方位角时。在α为15.0°～30.0°范围内,A区、B区迎风屋面μs表现为负值,且绝对值随α增加而减小,在α为37.5°～ 45.0°范围内其μs表现为正值,绝对值随α增加而增大;背风屋面C区、D区μs始终为负值,其绝对值随α增加而增大。

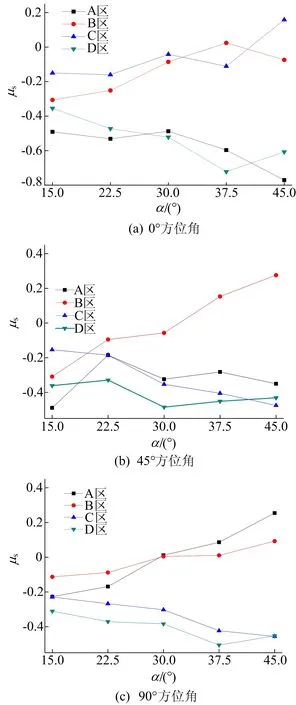
图12 各方位角下屋面分区μs随α变化曲线

总体分析表明,各方位角下迎风屋面μs随着α增大逐渐由负值向正值转变,表明迎风屋面受荷形式由受风吸力为主转变至以受风压力为主;背风屋面μs随着α增大整体表现为负值,随屋面α增大,背风屋面所受风吸力作用逐渐增大。

2.2 挑檐对屋面风压分布的影响

对α=15.0°的四坡屋面建筑设置挑檐,其建筑模型如图13所示。基于0°、45°、90°方位角研究挑檐对屋面风压分布的影响,挑檐长度l=1 m,挑檐高度h=1 m。

通过模拟分析,获得各方位角下屋面分区μs变化曲线,如图14所示。

图13 有挑檐的四坡屋面建筑模型

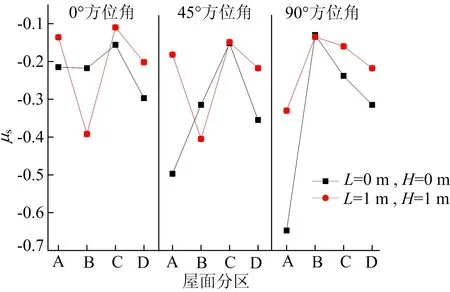
图14 各方位角下有、无挑檐时屋面分区μs

由图14可知,不同方位角下有、无挑檐时,各屋面的μs整体均表现为负值。0°方位角下增设挑檐后A区、C区、D区μs绝对值明显减小,最大减小41%,B区μs显著增大,约增大82%;45°方位角下,C区μs基本不变,B区μs小幅增大,A区、D区μs显著减小,其中A区减小最明显,约减小56%;90°方位角下,B区μs基本不变,其余3个区μs绝对值均有不同程度减小,其中A区减小幅度最大。

综上所述,挑檐的设置可以有效减小背风区的风压,对迎风屋面的影响效果显著,对局部屋面的影响略为增大,但对于整体屋面的μs起到减小的作用,表明挑檐的存在有利于减小四坡屋面建筑屋面的龙卷风荷载作用。

3 结 论

本文对龙卷风风场中的四坡屋面建筑风荷载进行数值模拟研究,基于不同方位角,分析屋面坡角以及有、无挑檐对四坡屋面风压分布的影响,获得以下结论:

(1) 龙卷风作用下,屋脊处易发生漩涡脱落产生较大负压,并形成较大的逆压梯度;随坡角增加漩涡脱落有所增强,背风屋面负压数值和范围不断增大。

(2) 各龙卷风方位角下,当屋面坡角较小时,迎风屋面大部分区域受负压作用。随着坡角增大,迎风屋面正压作用范围扩大。当坡角在30°～45°范围内,屋盖背风屋面靠近斜脊线区域出现较大负压;当坡角为45°时,迎风屋面正压较大,背风屋面整体受较大的负压控制。

(3) 龙卷风作用下,挑檐的存在对建筑物屋面风压分布具有显著影响,尤其表现在背风屋面,能显著降低背风屋面的风压,但会略增大局部区域的风压。总体而言,挑檐的设置能减小四坡建筑屋面的龙卷风荷载作用,针对挑檐形式和尺寸对龙卷风荷载的影响还需要深入开展研究。