三角网格分割中种子点的优化采样算法

徐源廷, 曹 力,2, 贾 伟,2

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230601)

0 引 言

近年来,随着3D打印、三维扫描、基于图像建模等技术的发展,许多三维数据采集设备应运而生,随之产生大量三维几何数据,将这些数据进行去噪、三角化、简化处理后才可以得到供使用的模型。将采集到的模型进行必要的三角网格分割,可以使用户更容易对这些模型进行曲面压缩、纹理映射、模型检索、网格重构、参数化等操作。对三维几何模型的网格划分,是提取模型轮廓线的一个常用办法。将三角网格模型分割为多个面片,其面片的边界线可作为模型的轮廓线。以VSA(variational shape approximation)[1]为代表的三角网格模型聚类分割算法是一种基于k-means的网格分割方式,常被用于面片划分、轮廓线提取等工作，但由于它采取随机的方式生成种子点,从而导致划分结果存在误差,提取的轮廓线不够精细。

本文提出一种三角网格分割中种子点的优化采样算法,可以通过类内再聚类、类间合并以及边界再划分的步骤优化三角网格分块结果,给出建议的初始种子点个数及位置。根据对多个模型进行试验表明,利用本文方法给出的种子点可以提取优质的轮廓线,该轮廓线重建模型效果更好。

1 相关工作

1.1 研究现状

原始采集到的三角网格模型往往缺少结构特征和语义信息,使计算机难以对其进行更高级的识别处理工作,由此引申出大量关于三角网格模型处理的工作。

三角网格分割[2]可以解决诸如纹理映射、模型重建、网格动画、参数化等问题[3],一直以来，很多学者提出不同研究方法[4-5]，文献[6-7]总结了一些网格分割算法,并提出改进途径。

针对分割目的或对象的不同,分割算法的侧重点也有所差别。当分割的对象是尺度较大的模型或者分割目的是为了纹理映射时,网格分割算法更加侧重整体分割,即分割为若干大的区域,细节的展示由纹理完成,因此分割过程中可以一定程度上忽略部分细节；例如基于分水岭的三角网格划分方法[8],这类方法首先根据几何信息确定盆地和分水岭,然后采用浸水方式或降水方式将模型分割为以分水岭为边界的集水盆地区域。文献[9]提出一种基于特征检测和核心提取的网格分割算法,该算法首先获取到网格的特征信息,如特征边、特征点,然后根据这些特征信息对网格进行划分。该类方法适用于一些较大的区域或部件,且略去了部分模型细节。

当分割的对象是较精细的模型或者分割以网格重建为目的时,不能忽略模型细节。文献[10]将网格数据划分为多个相同的单元,依据其密度分布进行划分,只有当密度不小于设定阈值才进行扩展；依据密度阈值的设定,可以控制划分粒度、展示模型细节。

另外基于可变网格,文献[11]提出一种动态增量的聚类算法,即当新的数据到来时,判断是否属于现有划分区域；若是，则加入,否则新建一个类。该方法避免了k-means算法需初始设定聚类数的问题,但无法在一开始提供推荐种子点个数或位置。还有一些网格聚类分割工作[12-14],针对应用场景不同、采用策略不同均提出自己的优化算法。

除采用聚类分割以外,文献[15]采用模型表面张量投票的方法,可以更加快速地对网格进行分割。文献[16]提出一种三角网格分割算法，应用在CAD方面;另外还有一些自适应算法[17-18]和约束关系[19]的网格模型分割。对于网格分割得到的区域边界,可以作为网格模型的轮廓线。

轮廓线提取对于三角网格模型的处理是至关重要的。文献[20]提出首先提取模型中角点,再依据角点间的某种拓扑关系,提取模型轮廓线;文献[21-22]提出一种网格顶点法向投票张量理论,进一步将顶点分类为角点、面点、尖锐边点;文献[23]在特征线的基础上,另外提取曲率方向一致、更加规整紧凑的曲线网格,得到的轮廓线有更好的重建效果。

关于模型重建的工作,文献[24]通过输入给定曲线或曲面上的采样点,通过直线或三角形连接这些样本得到多边形网格,以此重建三维模型;文献[25]将模型轮廓线信息作为输入,在轮廓线间穿插特定曲率曲线,使其平滑过渡轮廓线间曲率差距,自动补全网格信息,重建三维网格模型;文献[26]用基于L0范数定义法向量场的优化目标函数,使用变分逼近的方式对模型进行分割,拟合区域的B样条曲面进行合并覆盖,得到重建后模型的似可展曲面,最后再对可展曲面进行拟合优化得到最终的重建结果，该方法对带有噪声的模型也能有较好的重建效果。

1.2 变分形状逼近(VSA)算法介绍

变分形状逼近算法是最具代表性的网格模型聚类分割算法[1]是一种基于k-means的迭代聚类的三角网格模型分割算法,并广泛应用于轮廓线或特征提取的工作中。该方法通过形状代理代表带扩展区域,通过计算带扩展区域边界三角形到对应形状代理的距离,进行区域扩展,并通过不断迭代直到收敛,最终得到划分结果。文献[27-29]在其工作基础上进行改进,分别采用不同的形状代理进行拟合,以达到更好的逼近效果。

其中计算三角形与代理之间的距离度量采用L2,1距离,定义为:

(1)

其中:Ri为待扩展区域;Pi为区域代理;n(x)为待扩展区域法向;ni为区域代理法向。以此来刻画区域代理与区域边界三角形间的误差。

2 网格分割

2.1 变分形状逼近(VSA)不足

变分形状逼近作为一种基于k-means的迭代聚类算法,种子点的选取尤为重要，种子点的数量直接决定了最终分割的块数。假设一个模型被划分为n个区域为最佳,而当种子点选取个数小于n时,会使得原模型中理应被多个区域的部位被划分为一个区域;当种子点数大于n时,则会出现理应被分为一个区域的部位被分为多个区域。当种子点的位置选取不适当时,可能会陷入局部最优,很难迭代出正确的划分结果,这种情况下只能重新选取一组新的种子点。不同种子点对VSA分割效果的对比如图1所示。图1a、图1b均为使用VSA方法对Fandisk模型选取不同种子点进行网格分割的效果,可以明显看出，图1a的黑色方框中所示部分出现一些分割错误,分割效果不如图1b。

图1 不同种子点对VSA分割效果对比

由此可见，种子点的选取个数以及位置对于三角网格模型的处理是非常重要的。

本文基于三角网格模型,以VSA的算法思想为基础,提出一种种子点的优化采样算法,可以提取网格模型中近似合理的种子点个数及位置。

2.2 网格划分误差分析

现有三角网格划分算法因其自身局限性,难以适用于全部模型,其划分结果往往存在一定误差,本文以VSA方法为例,将此类问题产生的误差分为如下3种。

(1) 过度分割。当在三角网格模型M上选取n个种子进行VSA聚类分割时,因其种子点选取的随机性,会对划分结果造成不可预计的错误。当2个种子点同处一个平面上时,其采用加权平均法得到代理面法向信息,此时得出的2个代理法向完全相同，导致在迭代完成后将一个平面错误分为2个分块,此时便出现过度划分的情况如图2所示。

图2中黑色方框处即错误地将一个平面分为2个区域。

图2 过度分割现象

过度分割的情况会使轮廓线的数量增多,而这些额外的轮廓线并不包含模型的轮廓特征,从而造成了后续模型重建过程中时间上的浪费。

(2) 稀疏分割。在使用VSA方法进行网格分割过程中,若模型最佳分块数为n,而种子的初始选取个数小于n,则在划分的结果中,会出现将本应划分为多个部分的区域错误划分为一个部分,这种情况称为稀疏分割现象,如图3所示。图3a黑色方框橘色分区部分包含模型多处轮廓线,却错误地将其划分为一个部分,应进行进一步划分。

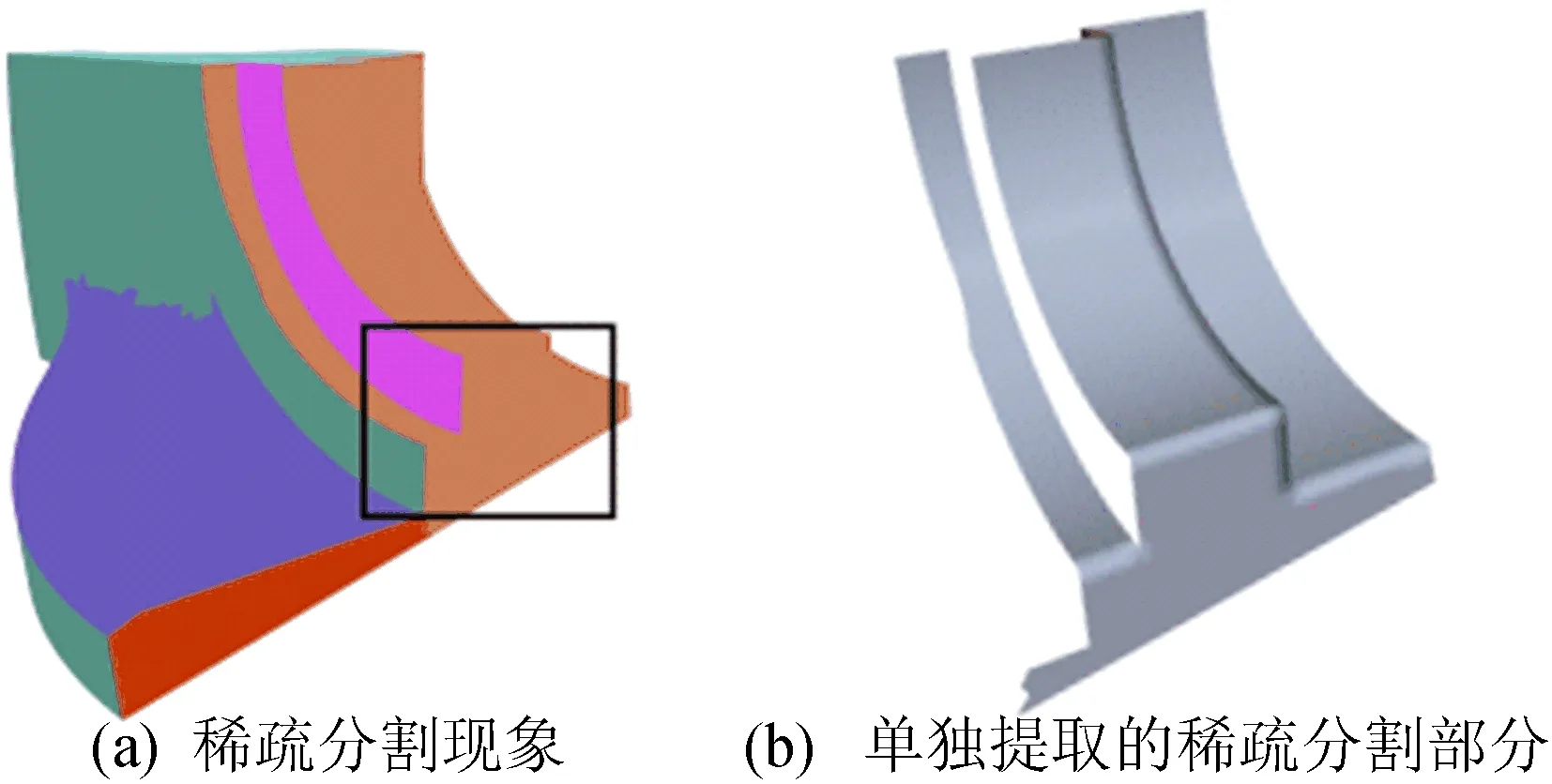
图3 稀疏分割现象和单独提取的稀疏分割部分

稀疏分割现象会导致提取的轮廓线无法包含模型所有的轮廓线,从而导致根据轮廓线进行模型重建的结果出现错误。

(3) 边界误差。因各种网格划分算法的局限性,对于边界三角形,对其归属分块的判断出现错误,造成边界误差。对于边界三角形所属分块划分错误，如图4所示。

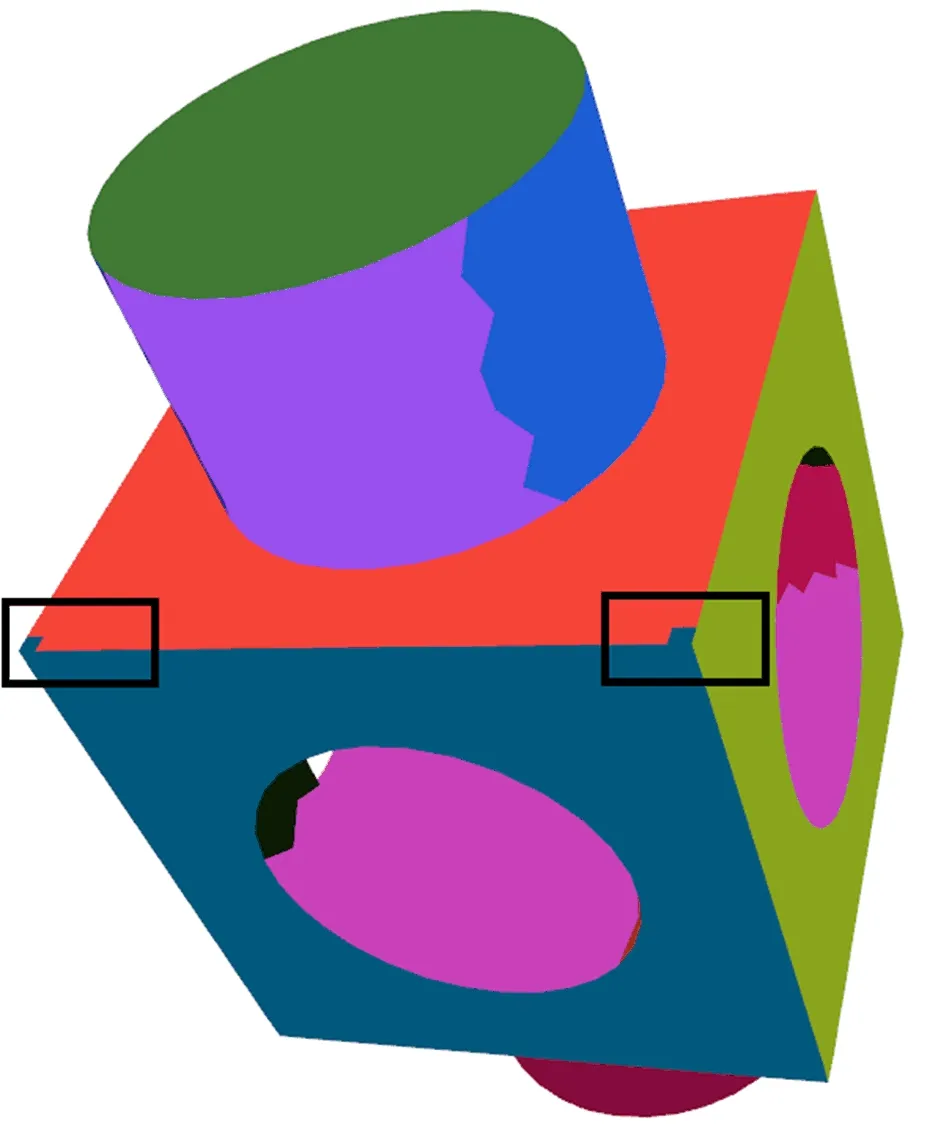
图4 边界误差现象

边界误差现象会导致最终划分结果出现错误,提取的轮廓线不够平滑。

3 算法流程

本文在VSA方法思想的基础上,针对以上具体问题,做出一种改进。对以上中提到的过度划分、稀疏划分和边界误差的现象,分别采用类间合并、类内再聚类以及边界再划分的方法进行处理。处理流程图如图5所示。

图5 处理流程

3.1 类间合并

采用VSA方法一步划分完成后,首先处理由于种子点选取过密而引起的过度划分现象,对于每个区域分块,计算其与相邻区域代理间的L2,1距离,若小于设定阈值(本文为0.02),则说明2个区域十分相似,视为2块区域出现过度分割现象。将三角面较少的分块合并到较多的分块中,并删除该分块。类间合并处理后的效果如图6所示,由于图2中底部2个分块代理的L2,1距离趋近于0,将2个部分合并为一个分块，从而消除过度分割现象。

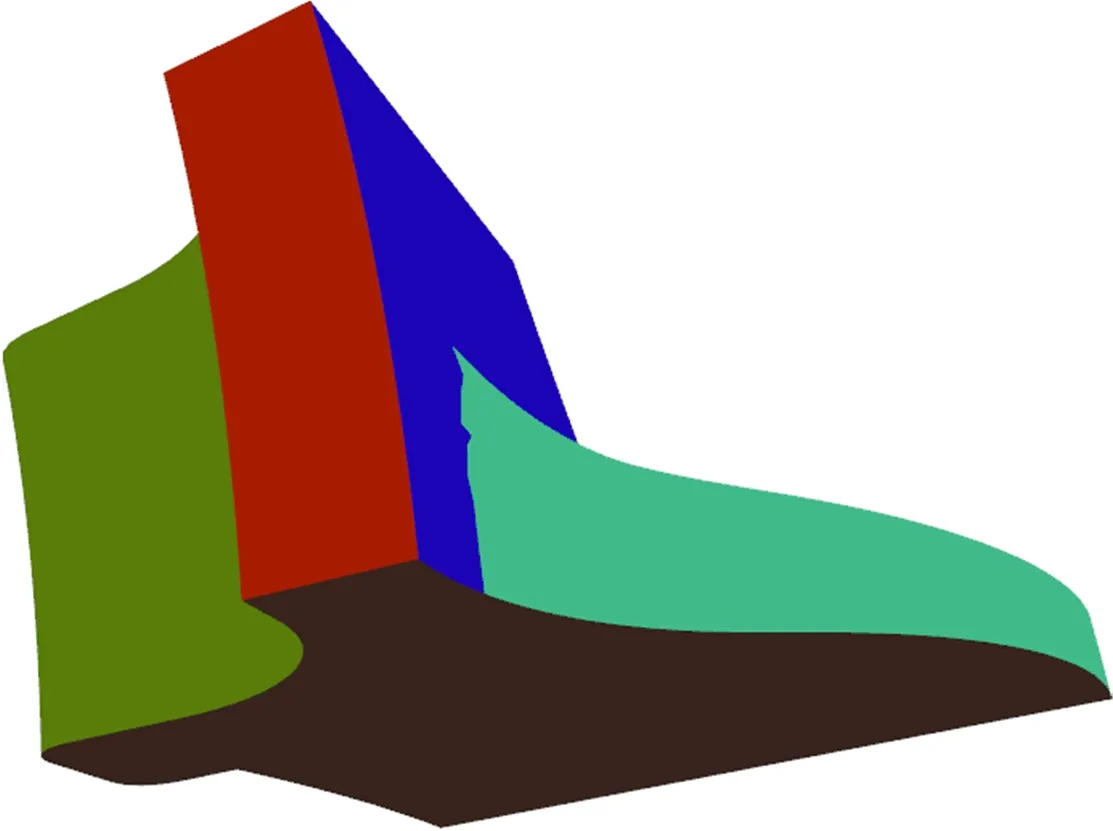
图6 类间合并处理效果

3.2 类内再聚类

对于划分后的每个区域,单独提取,计算其分块内所有三角形的单位法向方差；若需要其方差大于设定阈值,则该区域出现稀疏分割现象,需要对该区域进行进一步划分。类内再聚类处理效果如图7所示,将图3b中稀疏分割部分单独提取并进一步划分,直至任一区域的三角形法向方差均小于设定阈值。

图7 类内再聚类处理效果

这里之所以先进行类间合并再进行类内再聚类,主要是因为如果先进行类内再聚类再进行类间合并,那么最后的类间合并可能会导致误差堆叠,使得一个区域内的单位法向方差重新大于原设定阈值。因此这里先进行类间合并再进行类内再划分。

3.3 边界再划分

为保证最终划分结果边界平滑无误差,对于区域边界三角形,判断其与所属划分区域代理面的L2,1距离,当大于设定值时,视为出现边界误差。对该三角面进行边界再划分处理,计算其与相邻区域代理的差值,将其划分到差值最小的区域中去。边界再划分处理效果如图8所示,将图4中黑色方框中三角形再划分,得到较好效果。

图8 边界再划分处理效果

3.4 更新种子点

将最终划分结果,对每个区域计算其平均法向及平均重心作为区域代理,找出与每个区域代理距离最为相近的三角形,作为新的种子点。

3.5 模型重建

利用上一步提取的种子点个数y及位置,重新进行三角网格划分,提取模型轮廓线并进行模型重建,对比重建模型与原模型间的差距。本文采用模型间Hausdorff距离[30]来表示模型间的差距,同时对比选取不同种子点个数时重建出的模型与原模型的Hausdorff距离。

选取不同种子点时,重建模型之间的效果对比如图9所示。利用本文算法推荐种子点个数为18。不难看出当种子点个数小于18时,可以明显观察到重建误差；当种子点个数大于18时,对重建模型的质量影响不大。

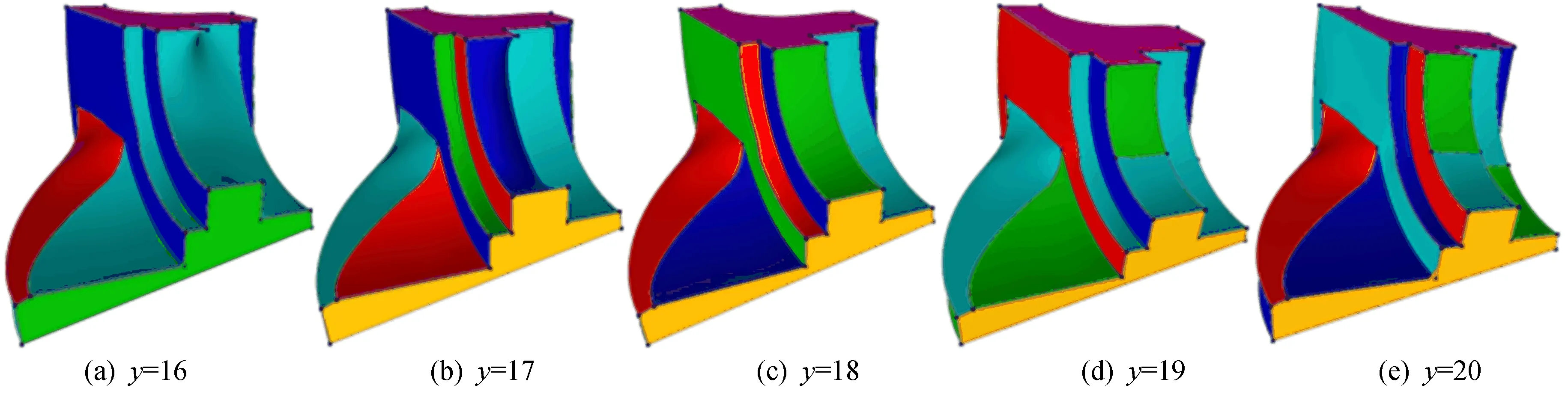
图9 不同种子点对应重建效果对比

为客观展示重建差距,不同种子点重建模型与原模型Hausdorff距离对比如图10所示。从图10可以看出，当种子点个数不断增加时,重建模型与原模型之间的Hausdorff距离呈下降趋势；而当种子个数为18时,重建模型与原模型之间的Hausdorff距离已基本收敛,不再变化。

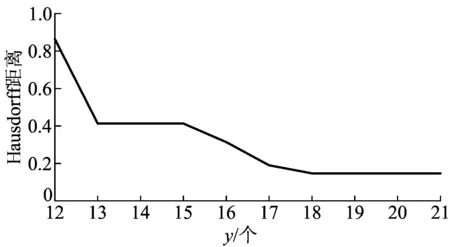
图10 不同种子点重建模型与原模型Hausdorff距离对比

4 实 验

本文借鉴VSA方法思想,将网格模型分割结果进一步进行类间合并、类内再聚类以及边界再划分,优化三角网格模型的聚类划分结果,从而提取出推荐模型种子点。利用该种子点可以提取优质模型轮廓线,从而重建出的模型更加贴近原模型。

所有对比实验均在配置为Intel 1.90 GHz(2处理器)、8 GB内存、GTX 1060 3 GB显卡的图形工作站上完成。

4.1 模型重建工具

对于最终划分计算得到的模型轮廓信息,本文模型重建采用文献[13]的方法。该方法通过输入模型轮廓线信息,可以在所给出轮廓线之间平滑地插入特定曲率曲线,使得模型表面曲率变化与给出的轮廓线自动对齐,最小化不好的曲率变化。自动构建模型表面三角网格,使模型曲面上的主曲率方向与轮廓线所表示的光滑流场一致性保持最大，最终输出off格式的模型文件。经过对比,该方法具有较好的模型重建效果。

4.2 重建模型对比

本文分别采用raised、joint、bird以及gear 4个模型,选取不同种子点数目进行重建模型对比实验，结果如图11～图14所示,其中每幅图中的图b为采用本文方法计算出的种子点数目进行模型重建所得效果；图a为种子点数目小于计算值时的重建效果,图c为种子点数目大于计算值时的重建效果。

可以看出,当种子点数小于计算值时,raised模型和joint模型均发生了一定程度的扭曲变形,bird模型和gear模型则出现了明显的重建错误,bird模型的左侧翅膀部分下截面凸出到上截面上,gear模型的中间齿轮部分出现空洞。而当种子点数大于计算值时,可以看出与中间结果相差不大,只是增加了部分可有可无的轮廓线而已,而这些多出的轮廓线,对模型描述的作用并不大,反而会带来不必要的资源消耗。

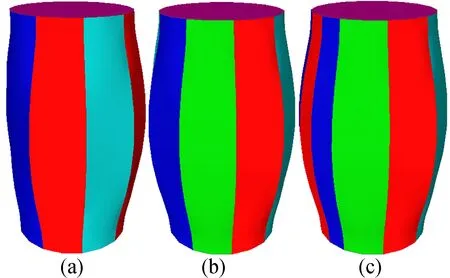
图11 raised模型种子点不同时重建效果

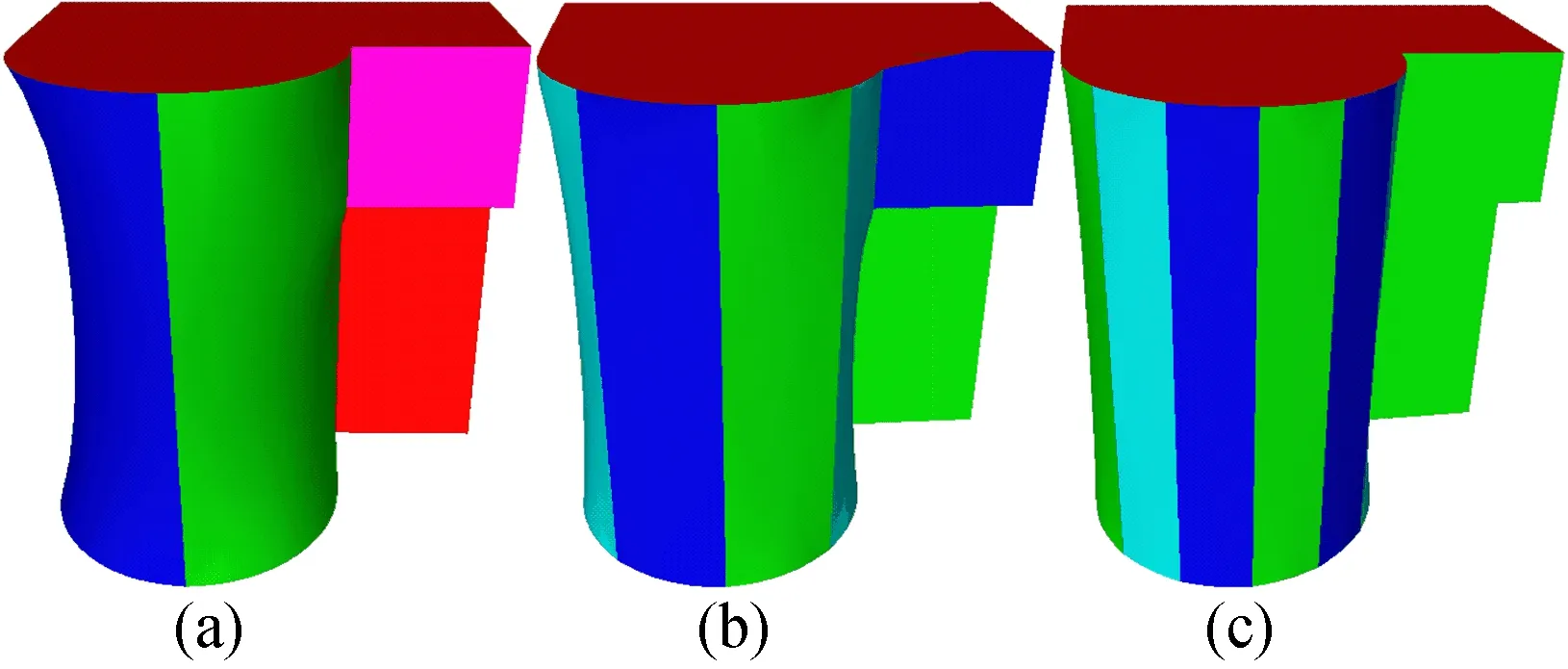
图12 joint模型种子点不同时重建效果

图13 bird模型种子点不同时重建效果

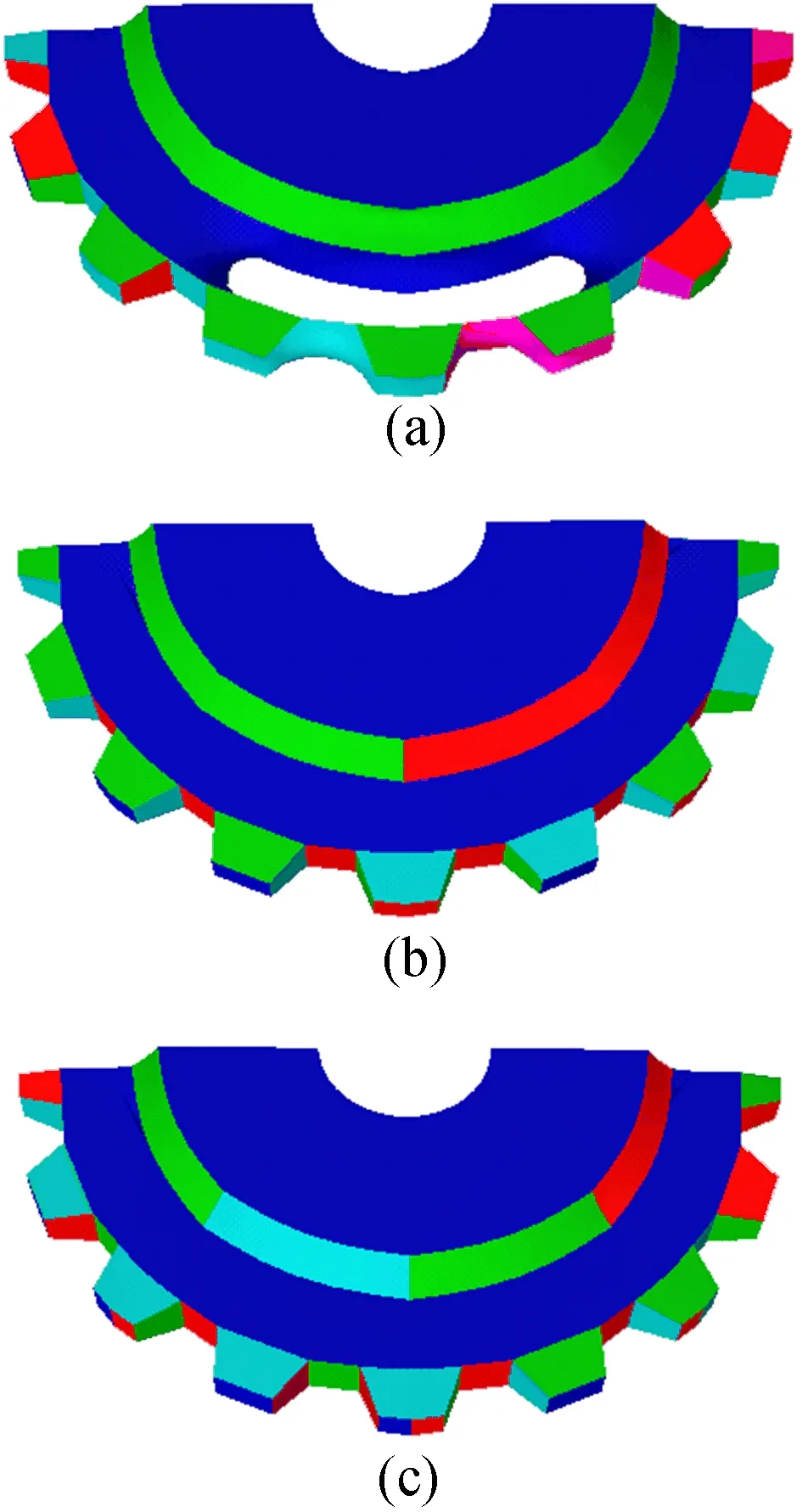
图14 gear模型种子点不同时重建效果

选取种子点数目见表1所列。由表1中对比重建模型与对应重建模型的具体误差数据可以进一步佐证本文观点。其中SN(seed number)代表种子点数目,HD(Hausdorff distance)代表对比原模型的Hausdorff距离。数据列(1)、(2)、(3)分别代表种子点数目小于、等于、大于计算值时,对比原模型的重建误差。可以看出,由列(1)到列(2)误差降低明显,由列(2)到列(3)误差降低不大。

表1 不同种子点数目与原模型误差对比

5 结 论

本文针对三角网格分割中常见的过度划分、稀疏分割、边界误差三类问题,进行检测,并分别采用类间合并、类内再聚类、边界再划分的方式逐一进行处理,最小化区域内三角形法向方差。从优化后的划分区域中以加权平均的方式选取推荐种子点。

通过实验表明,在种子点选取个数递增的情况下,采用提取轮廓线并进行模型重建的方式,其结果与原模型之间的Hausdorff距离呈下降趋势,逐渐趋于曲线收敛。采用本文方法提取的种子点个数可以接近收敛处的种子点个数。进行轮廓提取模型重建时,可以保证在种子点个数尽可能少的情况下,保证重建模型质量,使其与原模型之间差距更小,结果更为精确。