结构光数字微镜投影系统的条纹质量演变*

2021-04-06张嘉霖王建华杜虎兵

西安工业大学学报 2021年1期

张嘉霖，王建华，杜虎兵，赵乐

(西安工业大学机电工程学院，西安 710021)

结构光三维测量技术由于具有结构简单、非接触性以及易于实现自动化等优点[1]，在测量领域占有极其重要的地位，也是测量领域的研究热点之一[2]。伴随着以数字微镜(Digital Micromirror Device，DMD)为结构光发生器的数字光处理(Digital Light Processing,DLP)投影技术的快速发展，以及各种解相算法的出现，使结构光三维测量技术能够实现高分辨率、高精度和高速度的三维测量[3]，并广泛应用于工业、医学检测、文物数字化等领域[4]。

结构光三维测量技术大多基于相位测量，而相位是从摄像机采集到的变形条纹图中解调出来的[5]，因此投影条纹的质量直接影响待解调相位的计算精度。文献[6]采用DLP Discovery实现对二值光栅条纹图的高速切换，结合相移法实现了超高速三维形貌测量，其速度高达667 Hz，并在实验中实现对悬臂梁振动状态动态观测，但其中并未考虑到投影条纹误差对测量结果的影响。文献[7]设计开发了一套快速高精度的三维测量系统，用可编程DMD投影仪实现高速高精度条纹投影并同步清晰采集，测量精度可达10 μm，其中关于非正弦性导致的解调误差，采用了三频外插算法进行了补偿，忽略了条纹本身对解调结果的影响。文献[8]通过三维重建过程分析得出光栅周期数的增加可以降低立体匹配的误差，然而周期数的增多会产生量化误差，降低测量精度，实验了不同光栅周期数对系统测量精度的影响，并为系统选择了一个最优的光栅周期数，其中缺乏相应的数学理论推导及评价模型。文献[9]认为高精度的轮廓往往受到非线性响应的影响，提出了几种常用的相位误差校正方法，如查找表补偿法、强度校正法、伽玛校正法以及灰度编码和彩色编码的相位误差抑制方法，采用算法对投影条纹校正和补偿，其中并未涉及条纹质量的问题。

因此，本文将搭建基于数字微镜的结构光投影系统，分析结构光数字投影系统的响应过程，建立分析评价条纹质量的数学模型，推导评价条纹对比度及正弦性的数学表达式，结合仿真与实验验证的方式，研究投影条纹质量的演变规律，最终通过建立与物理光栅的比对实验客观评估基于数字微镜的结构光投影系统的条纹质量。

1 结构光投影系统条纹质量评价

1.1 非正弦现象

在室内暗场的条件下，用可编程DMD投影仪投射出一组条纹图，图像分辨率为912 pixel×1 140 pixel，对比度为1，并对采集图像中间行(第600行)进行平铺分析，得到实际采集条纹图像的光强分布。为了更加清晰地表述，对采集图像光强分布进行傅里叶变换，得到实际光栅频谱图，通过频谱搬移的平移处理，使得频谱图的零频分量显示在图像中心，如图1所示。

图1 数字投影系统的非正弦现象Fig.1 The nonsinuous phenomenon of the digital projection system

通过采集图像的光强分布可以看出，相比理想的标准正弦的光强分布，出现了“平台”现象，CCD相机实际采集的条纹图光强分布大致在50～250之间。通过对比分析，理想频谱图仅有一次低频谐波分量，而实际的频谱图中存在多次谐波分量，因此导致了非正弦现象。

1.2 数字投影系统光强传递函数测定

针对实际采集图像所存在的非正弦现象，采用光强传递函数来描述光强信号的传递过程。通过逐一投射不同灰度的图像，分析投影系统线性输入灰度与输出亮度之间的对应关系，测量系统的光学强度传递信号，分析其非线性效应[10]。实验利用光照度计测量可编程DMD投影仪实际输出的光强信号，得到可编程DMD投影仪的光强传递函数的测试曲线,如图2所示。

图2 数字投影系统光强传递函数曲线Fig.2 IFT curve of digital projection system

该函数的具体测量方法[11]:① 计算机编程生成256张24 bit的灰度图片，灰度从0变化到255;② 灰度图像通过可编程DMD投影仪按顺序依次投射出来，形成一个线性的数字输入信号greyi(n)。

投影仪的光强输入信号greyi(n)可表示为

greyi(n)=n。

(1)

式中：n= 0，1，2，…，255。

根据实测的光学传递函数曲线可以看出，对于计算机输入的线性变化的光强信号，光功率计接收到灰度分布曲线不再符合线性变化规律，说明了可编程DMD投影仪具有非线性输出的响应特性。因此，如果直接对可编程DMD投影仪输入标准的正弦条纹信号，由于光强传递函数的影响，使得输出的信号将不再是标准的正弦信号。

1.3 数字投影系统响应模型

针对投影条纹的非正弦现象以及实际光强传递函数的测定结果，分析投影过程中的光强分布，建立投影系统的数学响应模型。其响应过程[12]：通过计算机编程生成待投影的图案，经过可编程DMD投影仪投射至标准白色平板表面，再由摄像机采集投影图像，最终将采集图像传送至计算机，进行下一步实验分析。每个阶段的非线性响应叠加共同导致了采集条纹图像的非正弦光强分布现象。

由计算机程序生成初始的光强信号呈正弦规律分布的条纹图，生成的理想静态条纹可以表述为

In(x,y)=a(x,y)+b(x,y)cos[φ(x,y)]。

(2)

式中：a(x,y)、b(x,y)分别为背景灰度和调制强度。

由投影仪投射至标准白色平板表面后，考虑到标准白色平板表面的反射及实验环境光等因素的影响，标准白色平板表面光强[13]的表达式改写为

Ip(x,y)=RIn(x,y)+C。

(3)

式中：R表示物体表面反射率；C表示环境光。

此时，投影光线进入CCD相机，此时在相机中条纹的光强分布为

Ir(x,y)=fr(Ip(x,y))。

(4)

1.4 条纹质量评价模型理论推导

一般地，结构光测量系统的响应为系统输入与系统点扩散函数(Point Spread Function，PSF)的卷积，因此CCD相机接收到的光强为

fr=h(x,y)。

(5)

即Ir(x,y)=Ip(x,y)×h(x,y)。

(6)

式中：h(x,y)为系统的点扩散函数[13]且：

(7)

式中：σ=AD，A为常数，D为系统的入瞳直径；D=f/F，f为相机镜头的焦距，F为相机镜头的光圈数[13]。

Ir(x)=F-1{F(Ip(x))F(h(x))}。

(8)

因此，式(8)可改写为

(9)

条纹图像对比度：

(10)

对式(9)进行傅里叶级数变换展开，并将ω=2π/T、σ=AD、D=f/F代入式(11)，通过其基频幅值与其余倍频和的幅值表征条纹的正弦性，即其正弦性可表示为

(11)

理想频谱图仅含有一次低频基波，且幅值很大，而实际的频谱图中存在高次谐波分量，导致实际采集的条纹具有非正弦性；若基频相对其余谐波占比大，说明采集条纹光强分布正弦性更好，而五次以上的高次谐波分量非常小，其对系统的影响可以忽略。因此，理论推导过程中倍频数仅考虑到五倍频对非正弦现象的影响。

根据条纹质量评价模型的理论推导，采集到条纹的对比度和正弦性由反射率R、环境光C、背景灰度值a、镜头焦距f、周期T、调制度b以及相机光圈数F共同影响。当系统搭建完成后，反射率R、环境光C、背景灰度值a、镜头焦距f均为固定值。因此，评价条纹的对比度和正弦性仅由可调节的系统参数周期T、调制度b以及相机光圈数F决定。

2 实验及分析

2.1 条纹演变规律仿真结果及分析

根据理论推导的影响条纹质量的参数，建立仿真实验，验证条纹对比度和正弦性与条纹的调制度b、周期T以及相机光圈数F的数学关系式，仿真不同调制度、周期及F数的条纹对比度与正弦性，如图3～4所示。

图3 仿真得到的系统参数与条纹对比度的关系Fig.3 Relationships between system parameters and contrast ratio of fringe pattern obtained by simulation

仿真结果可以得到：投影条纹的对比度与调制度和光圈数F呈正比，并且对比度随着周期增大而增大。投影条纹的正弦性与调制度和光圈数F呈反比；并且随着周期的增大，正弦性降低。

图4 仿真得到的系统参数与条纹正弦性的关系Fig.4 Relationships between system parameters and sinuousness of fringe pattern obtained by simulation

2.2 条纹演变规律实验结果及分析

为了验证理论推导及仿真结果中系统参数对采集条纹对比度和正弦性的影响。在保证实验暗室的条件下，减小背景光对实验结果影响。搭建实验平台，将计算机生成的标准正弦条纹图像投射到标准白色平板上，CCD相机采集不同条纹周期数、调制度以及不同光圈数下的条纹，并对条纹的对比度与正弦性进行实验分析。

搭建的数字投影系统可以划分为三个主要模块：可编程DMD数字投影模块(DLP Light Crafter 4500)、图像采集模块(BFLY-U3-50H5C-C)以及相关的上位机控制模块，系统实验装置图如图5所示。

图5 数字光栅投影系统实验装置图Fig.5 Picture of experimental digital projection system

实验中CCD相机的光圈数F分别为2.8，4，8以及16，条纹的调制度b分别为：0.05，0.10，0.20，0.30，0.40，0.45以及0.50，条纹周期T分别为15 pixel，30 pixel，40 pixel，50 pixel，80 pixel，100 pixel和150 pixel，不同条件下CCD相机拍摄的条纹图如图6所示。不同系统参数下对比度与正弦性实验结果如图7和图8所示。

图6 不同系统参数下CCD相机拍摄的条纹图Fig.6 Fringe patterns captured by CCD camera under different system parameters

图7 实验得到的系统参数与条纹对比度的关系Fig.7 Relationships between system parameters and contrast ratio of fringe pattern obtained by experiment

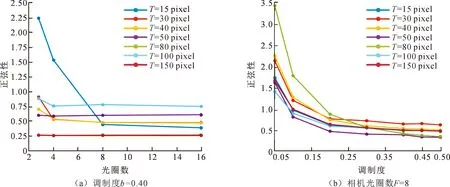
图8 实验得到的系统参数与条纹正弦性的关系Fig.8 Relationships between system parameters and sinuousness of fringe pattern obtained by experiment

条纹对比度的实验结果与仿真结果基本一致，当条纹的调制度与周期一定时，采集条纹的对比度随相机光圈数F增大而增大；当条纹的F数与周期一定时，采集条纹的对比度随着调制度增大而增大；且对比度随周期的增大而增大。条纹正弦性的实验结果与仿真结果趋势基本一致，当条纹的调制度与周期一定时，采集条纹的正弦性随F数增大而降低；当条纹的F数与周期一定时，采集条纹的正弦性随调制度增大而降低。在周期数T的影响方面，条纹正弦性的实验结果与仿真结果存在差异，是因为DMD和CCD是数字器件，在数-模转换过程中存在量化误差的影响[14]，投影条纹周期数与量化误差的耦合作用，在条纹周期数T处于80～100 pixel时，达到了一个平衡状态。

通过结果分析可以得到，当条纹周期数T处于80～100 pixel，调制度为0.2～0.4及相机镜头F数为4.0～8.0时，能够得到对比度趋近于1、且基频分量高的高质量正弦条纹。

2.3 结构光投影系统条纹质量评估

在结构光投影测量系统中结构光发生器是其关键组成部分，传统的产生光栅条纹的方式是通过光源透过物理光栅时的衍射及干涉作用形成条纹，但是物理光栅的栅距固定，且在相移法中需要通过相移器实现相移。为了评估本文所搭建结构光投影系统的条纹质量，因此设计与物理光栅的条纹质量比对实验。

白色光源发出的光线经过物理光栅(栅距为200 μm)，通过透镜扩束，水平投射在标准白色平面上，CCD采集标准白色平面上的条纹图像，得到采集到的条纹图像对比度为0.269 23和正弦性为1.103 31。实验中，调节DLP投影仪LED光源输出分别为低亮度模式(LED光源，红∶绿∶蓝=50∶50∶50)与高亮度(LED光源，红∶绿∶蓝=104∶135∶130)模式，设置DLP数字光栅条纹周期为15 pixels，不断调节系统参数中的调制度，得到对比度与正弦值见表1。其中与低亮度模式下调制度b=0.30时、高亮度模式下调制度b=0.30时的比对结果如图9所示。