贝叶斯网络的结构学习综述*
2021-04-06吕志刚王洪喜邸若海
吕志刚,李 叶,王洪喜,邸若海
(1.西安工业大学 机电工程学院,西安 710021;2.西安工业大学 电子信息工程学院,西安 710021)
机器学习的核心问题是模型的建立,而贝叶斯网络(Bayesian Networks,BN)已被证明是一种有效且通用的模型学习工具,起源于1763年BAYES T发表的《An Essay Toward Solving a Problem in the Doctrine of Chances》。作为一种概率图形模型(Probabilistic Graphical Model,PGM),BN将图论和概率论相结合来更深层次的表示联合概率分布,不仅可以从数据中学习出潜在的模型,而且可提供领域知识的结构化表示,从而帮助人们在不确定领域中完成推理和决策任务。
近年来,人们不再局限于仅仅使用BN进行简单的知识建模,而是将其应用延伸至更具体的领域,诸如军事领域中的目标识别与多目标追踪技术,工业领域中的故障预测与健康管理(Prognostics Health Management,PHM)技术与可靠性分析、图像处理以及金融领域的经济风险分析等[1]。在某些领域甚至超过深度学习,比如参数估计,BN依托于贝叶斯公式可以对参数的统计特征给出可靠的描述,而深度学习是一个“黑盒子”,无法保证参数估计的可解释性。BN可以广泛应用于众多领域,究其原因在于其拥有严格的数学语言和图论语言,具有极强的逻辑性。而目前人们对于BN的精度、学习速率、处理复杂系统和连续变量的能力提出更高的要求,由此引发了BN研究的热潮。
从算法角度看,BN学习包括结构学习和参数学习两部分,参数学习建立在结构已知的基础上,因此网络的结构学习是关键,但这项任务已被证明是非确定多项式(Non-deterministic Polynomial,NP)难题[2-3]。BN的结构学习算法可以分为精确学习算法和近似学习算法。精确学习算法将BN推理和学习问题表述为函数的优化,通过遍历整个搜索空间,可以保证找到全局最优解,但受限于内存量和运行时间,目前最多应用在26个节点的网络中,通过加入约束来提升算法的性能是目前研究热点之一;近似学习算法通过有效元启发式算法对可能解的空间进行搜索来获得良好的解。本文将近似学习算法分为基于独立性检验、基于评分搜索和基于混合搜索三种,精确学习算法分为整数线性规划、A*和动态规划三种进行分析及归纳总结。
1 贝叶斯网络
贝叶斯网络定义:由结构G和参数Θ两部分组成。结构G为一个有向无环图G=(V,E),其中节点变量集合为V={X1,X2,…,Xn},有向边集合E描述变量间的依赖关系。参数Θ为一组条件概率分布,每个节点存储其自身与其父节点集合之间的条件概率分布,即P(Xi|Pa(Xi)),Pa(Xi)代表Xi的父节点集。同时贝叶斯网络也包含定性和定量两部分内容。G是模型的定性知识表示,用于描述变量间的概率依赖关系或独立关系,弧的方向具有因果定义,可进行因果推理;Θ是模型的定量知识表示,用于表述变量之间的概率依赖程度。
基于条件独立性假设(马尔科夫假设),贝叶斯网络进行了联合概率分布P的分解,将P分解为
(1)
式中:n为节点数;Xi为第i个节点,可取离散值和连续值;Pa(Xi)为Xi的父节点集。若网络中所有变量均为离散值,则称为离散贝叶斯网络;若所有变量均为连续值,则称为连续贝叶斯网络;除此之外的网络均称为混合贝叶斯网络。
2 完备数据下的BN结构学习
BN结构学习的主要思想是基于生成数据的样本集合,在推理所得到的若干个贝叶斯网络中,选出一个最符合给定数据集逻辑,拟合效果最好的网络结构。而其难点在于搜索空间会随节点数n的增加呈指数型飞涨。
贝叶斯网络结构的构造方法有两种,一种是通过专家的领域经验手工构造,另一种是通过数据分析来获得。前者适用于网络变量少,且变量之间具有明显的因果关系的网络结构,缺点是具有明显的主观判断,从不同的变量顺序出发会得到不同的网络结构。针对此问题,2000年,文献[4]提出按照因果关系来决定变量顺序。后者基于数据挖掘的各种算法来获得和数据集拟合度最高的贝叶斯网络结构,缺点是精确算法无法在有限的时间内找到最优解,近似的启发式搜索方法无法获得最优解。
完备数据下,BN的近似结构学习算法可分为基于独立性检验、基于评分搜索和基于混合搜索三类。
2.1 基于独立性检验的结构学习
独立性检验的方法将BN网络看作表示独立变量关系的网络模型,通过计算节点间的互信息和条件独立性找出各个节点之间的关系来判断网络中边的存在性,最终找到一个符合独立关系的网络结构。其中,互信息表示一个变量包含另一个变量信息的程度;条件独立,类似于d-分隔,则用来表示一个变量的改变是否会影响另一个变量。其中,d-分隔是图论的概念,而条件独立是概率论的概念。
1991年,文献[5]提出SGS算法,该算法从无向图出发,使用CI测试进行边定向。优点是不需要预先知道节点序;缺点是需要指数级的CI测试。2001年,文献[6]提出PC算法,该算法从一个完整的无向图开始,并根据CI决策递归删除边,从而产生一个无向图,然后对其进行部分定向和进一步扩展以表示基础DAG(Directed Acyclic Graph)。文献[7]展示了PC算法的适用性,即使在n=1 000的高维环境中,该算法也适用。优点是当基础DAG是稀疏网络时,该算法不仅可以减少运算量,而且可以采用卡方检验或互信息检验,不需要特定的CI测试。文献[8]提出了一种基于贝叶斯得分测试的方法。缺点是标准PC算法依赖于变量的排序,导致该方法出现不稳定的结果。因此,文献[9]提出利用骨架和V结构来改进定向规则,使PC算法性能与其变量顺序无关并显著提高了算法的鲁棒性。2002年,文献[10]提出三阶段算法(TPDA),三阶段分别是Drafting,Thicken和Thinning。该算法的优点是可以处理已知节点序情况,时间复杂度为O(n2),也可处理未知节点序的情况,时间复杂度为O(n4),并且在时间性能和准确度方面均优于PC算法。还提出了TPDA-Ⅱ算法[11],该算法以节点序为输入,并包含一些启发式算法以提高算法效率。2003年,文献[12]提出MMPC算法,该算法所需样本取决于生成的图的连通性,而不是局部区域的大小,因此可节省多达指数级的样本量。同年又通过引入低阶多项式算法,提出了IAMB算法[13]。2008年,文献[14]提出一种递归图分解学习贝叶斯网络结构学习算法,2009年,文献[15]在其基础上提出递归自主识别算法(RAI),该算法以一个完全无向图为初始图,并对其循环进行以下操作:① 对任意的两个节点进行 CI 测试,若独立,则去掉这两个节点之间的边;② 根据定向规则对边进行定向;③ 将图分解为自主子结构,对于每一个自主子结构,随着CI测试阶数的增加,递归调用RAI算法。创新点在于该算法首次将图的定向和分解递归运用到BN结构学习,不仅减少了CI测试的次数,而且避免了高阶 CI 测试带来的不可靠测试结果,学习到的网络结构精度也显著提高。2010年,文献[16]提出HPC算法,该算法结合增量方法和分治法的思想,使PC算法有能力处理较大的邻居节点集。2013年,文献[17]提出了LMM算法,用于提高从小样本数据中学习BN结构的准确性。该算法通过同时考虑节点对的条件独立性来改善对候选边缘的评估,并采用约束的自适应放宽,选择性地接受某些节点不以某些节点为邻居的条件。自适应放宽可以减少由于多次CI测试而导致真实边缘的移除。目前该研究领域创新性的引入了基于约束的局部因果发现方法的并行计算技术[18]。2017年,文献[19]在可用的计算单元中分配CI测试的基础上,提出了基于平衡的不完整块设计,实验证明该方法可在2000多个变量的数据集进行测试。2018年,文献[20]为了降低算法对CI测试错误的敏感性,提出一种学习树的算法,树中的每个节点代表变量子集的CPDAG评分,树的级别对应CI的最大顺序。实验证明该算法可以扩展到数百个变量,并学习到极好的MAP模型及变量之间可靠的因果关系。2019年,文献[21]通过结合多头绒泡菌数学模型和条件互信息理论对原始搜索空间进行修剪,并在多个数据集上进行对比实验,结果表明该算法在网络重构及原始数据匹配上具有较高的准确度。文献[22]创新性的提出基于MI的边缘去除策略和节点集生成策略,利用最弱的互信息优先策略来学习BN结构的WMIF算法。实验证明,该算法对条件集采取的策略不敏感且对节点序无要求,缺点是对于变量取值范围大的网络,需要充足的样本量。2020年,文献[23]提出了一种基于GPU的并行算法cuPC,该方法可以执行与节点序无关的PC算法,针对多元正态分布变量可以以cuPC-E和cuPC-S两种不同的方式并行化PC。实验表明,无论变量数量、样本数量和图密度,该算法都具有极强的可扩展性。
该类算法有两个弊端:① 均基于CI测试是可靠的假设,但实际得到的数据一般都会陷入CI测试的统计错误。② 当样本数据量较大时,算法复杂度将呈现为指数级;当贝叶斯网络节点个数较多时,CI测试的次数也呈指数级增长,会出现不可靠情况。因此,基于CI测试的方法更加适用于稀疏图。
2.2 基于评分搜索的结构学习
基于评分搜索的算法可以表示为:当给定数据集D={D1,D2,D3,…,DN}时,在搜索空间内找到一个结构G*使得:
(2)
其中Gn为变量集V={X1,X2,X3,…,Xn}在DAGs搜索空间中的所有可能结构。
基于评分搜索的结构学习把所有可能的结构视为定义域,衡量特定结构好坏的标准视为评分函数,将寻找最好结构的过程看作在定义域上求评分函数的最优值问题。从算法角度看,需确定合适的搜索策略和衡量DAG对数据适当性的评分函数。搜索空间可以分为三类:DAGs空间、等价类空间和节点序空间。虽然搜索空间不同,但其都分为父集识别和结构优化两个步骤。迄今为止,大多数研究都集中在结构优化上。
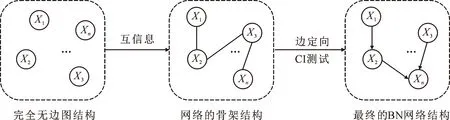
图1 基于独立性检验的方法流程Fig.1 Method flow based on independence test
2.2.1 评分函数
评分函数可分为两类,一类是贝叶斯评分函数,另一类是基于信息论的评分函数。由此产生的评分函数见表1。
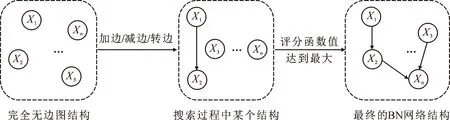
图2 基于评分搜索的方法流程Fig.2 Method flow based on score search

表1 评分函数总结 Tab.1 Summary of scoring function
最广泛采用的评分函数是BDeu和BIC,但BDeu等传统的评分算法只能应用于完整的离散变量[24]。
评分函数具有分数可分解性的重要属性:DAG的分数由每个变量Xi与其父集∏i得到的分数的总和构成,即
(3)
式中:G为网络拓扑结构;P(G)为其先验概率;D为数据集。
2.2.2 父集识别
父集识别即为每个节点挑选最优的父集,现有方法都要求对每个变量探索可能的完整父集空间,以便为预先计算的分数生成数据库。但该问题不接受具有质量保证的多项式时间算法,由此推动了启发式搜索技术的发展。
父集识别的常用方法是按顺序探索父集,首先父集集合包含空父集,然后是所有大小为1的父集,然后是所有大小为2的父集,以此类推,到达预先设定的k为止,其中k为任一节点所允许的最大父集数,称为最大度数,用于限制探索的复杂性。该方法的缺点是当变量的数量为n时,候选父集的数量随k增长O(nk),即n与k值的设置之间存在矛盾,n越大,k值应该设置的越小。
2008年,文献[25]设置k=2,可对n=1614的数据集进行结构学习。设置k≥3时,可处理的最大网络只有60个节点。2009年,文献[26]提出了修剪规则来解决n与k的设置矛盾问题,通过检测次优父集和允许丢弃搜索空间的一部分来减少探索父集空间所需的时间。缺点是并没有显著减小搜索空间的维数,当n较大时,k值仍不能设置的较高。2015年,文献[27]提出了对候选父集进行近似搜索的独立性选择算法,主要思想是通过一个恒定的近似评分函数BIC*来指导探索最有希望的父集,快速识别出最有前途的父集并计算分数。与顺序探索相比,该算法通过不同结构优化算法不断提高获得的分数,消除了结构约束k带来的限制,实验证明该算法可扩展到数千个节点;该算法的缺点是有效探索父集空间的过程仅适用于BIC,能否用其他评分函数是一个未解决的问题。2017年,文献[28]为解决精确的父集识别问题引入分布式存储父集的方法。为了实现可伸缩性,当使用MDL评分功能时,利用理论界限来约束搜索空间,并重新进行底层动态编程,从而提高计算速度。最终在Apache Spark平台中进行算法实现。实验证明,该算法可有效处理具有70个变量的数据集。
马尔科夫毯也可用于父集识别,一个变量X的马尔科夫毯MB(X)包括其父节点Pa(X)、子节点Ch(X)与配偶节点Sp(X)。如图3所示,节点5的父节点为{1,2},子节点为{3,4},配偶节点为{6,9},即MB(5)={1,2,3,4,6,9}。

图3 节点5的马尔科夫毯示例Fig.3 Example of Markov blanket at node 5
为了降低搜索空间的维数,对于某一节点而言,所有非马尔科夫毯变量都是冗余的,因此找出每个节点的MB进行父集识别即可。MB学习算法包括:① 基于全局条件独立特征的K&S、GSMB、IAMB、K-IAMB等算法;② 基于局部条件独立特征的MMPC/MB、PCMB、IPC-MB、MROR、DOS等算法;③ 基于逻辑回归分析的RA-MMMB算法;④ 基于评分+搜索方法的DMB和RPDMB两个算法。2020年,文献[29]提出利用Fast_MBD算法绘制出无向图,再利用kpath分解算法将整个网络分解成一系列子图,再利用MIIGA算法进行子图结构学习,最终按照组合规则输出完整的最优网络结构。
基于马尔科夫毯的算法都存在以下缺陷:① 设置的|MB|大小会影响最终生成的父集集合。|MB|过大,运行时间会缩短,但产生的MB中可能包含过多的假正元素,导致连锁反应;|MB|过小,会导致高时耗。② 局限于固定的搜索策略,搜索效率低,输出错误的或者不完整的马尔科夫毯的可能性较大。③ 受限于显著性门限值ε的设置。
2.2.3 结构优化
结构优化即在某个评分函数下,通过某种搜索策略缩小搜索空间来提高算法效率。当n>26时,寻找最优的结构是NP问题,因此常采用启发式搜索而非暴力求解。贪婪搜索算法作为最常用的启发式搜索算法,是一种局部搜索算法,易于陷入局部最优。为解决局部最优的问题,可采用迭代的方法改进解,包括基于单个解的优化算法(禁忌搜索、爬山算法、模拟退火算法等)和基于群体的优化算法(粒子群算法、遗传算法、蜂群算法、鱼群算法等)。
K2算法是由文献[30]于1992年提出的基于评分搜索的贝叶斯网络结构学习经典算法,具有非常优异的学习性能。但该算法需事先给出节点的顺序和每个节点的父节点个数的上限。2005年,文献[31]提出在变量排序空间上进行蒙特卡洛搜索,利用swap运算符为每个排序选择与其相符的最佳网络。该方法被证实可用于处理数千个变量的数据集。2011年,文献[32]提出了一种更强大的运算符:Insertion。使用该运算符,可以显著提高结构学习的评分。2017年,文献[33]提出给局部贪婪搜索加上扰动因子并利用遗传算法的思想,采用元启发式方法来提高局部贪婪搜索的性能。文献[34]提出一种对局部结构的基础顺序进行更改的方法,并证实该算法能够从包含数千个变量的数据集中学习网络结构并得到较高的评分。文献[35]将结构学习任务表述为通过标准数值算法解决的连续优化问题,利用连续算法进行求解。2018年,文献[36]提出一种基于PSO的学习BN结构的新方法,将质点的位置视为假想的似然性来表示相关边存在的概率,速度的增减来表示位置在飞行过程中的变化,将BN结构作为输出。实验证明,该算法可以有效地收集来自所有粒子的随机搜索信息,并得到BN结构。2019年,文献[37]在Jaya算法的框架下,结合遗传算法的交叉变异思想重新设计了个体更新策略,使Jaya算法能够应用于结构学习这一离散优化问题,并利用马尔科夫链理论证明了该算法的敛散性。实验结果表明,该算法能有效应用于BN结构学习。

表2 基于评分搜索的BN结构学习算法总结 Tab.2 Summary of BN structure learning algorithm based on score search
基于评分搜索的方法将结构学习问题看作优化问题,在不考虑学习效果和效率的情况下,可以利用现存的各种优化算法进行结构学习。对于单独学习效率差的算法,可以采用两种算法相结合的方式。
2.3 基于混合搜索的结构学习
混合搜索的结构学习结合前两者的优点,先利用统计分析学习效率高的优势来缩减网络结构空间的大小,再利用评分搜索网络结构空间,最终找到一个最优的网络结构。
CB算法是由文献[38]提出的第一个混合学习算法,该算法先用基于约束的PC算法确定节点的次序,再用K2算法进行结构学习;GBPS和PCGBPS算法是由文献[39]提出的混合学习算法,先用PC算法得到初始网络,再采用贪婪搜索法从该初始网络出发,在等价贝叶斯网络结构空间中搜索最优网络结构。MMHC是由文献[40]结合稀疏候选算法(Sparse Candidate Algorithm,SCA),提出的另一种经典的混合学习算法。该算法先采用最大最小父子 (Max-Mill Parents and Children,MMPC)算法构建BN的架构,再用K2算法确定出最优的网络结构。实验表明,无论从数据集的大小、时间复杂度和构建出的网络质量上看,MMHC算法都比许多其他算法优越。但该算法的缺点是当n很大时,算法第二阶段进行边定向的效率较低。并提供了Causal_Explorer下载链接http://www.dsl-lab.org/supplements/mmhc_paper/mmhc_index.html。该软件包可以直接调用MMPC、MMHC等算法。文献[41]提出了I-ACO-B算法,先利用CI测试降低搜索空间的复杂度,再利用蚁群算法对网络结构空间进行评分搜索,最终找到最优的网络结构。文献[42]通过改变评分搜索函数,利用人工蜂群算法(Artificial Bee Colony Algorithm,ABC)进行结构学习,该算法充分利用雇佣蜂所具有的局部寻优能力和侦察蜂对未知解的探索能力,保持了开发和探索的平衡,具有极强的全局搜索能力,从而保证尽可能找到全局最优解。
考虑到现实中大多数贝叶斯网络都是稀疏结构,文献[43]提出利用 L-1范数惩罚网络复杂度,并将正则项加入到评分函数中,有效减小网络结构复杂度,提高了计算效率,并将其应用在生物领域。2014年,文献[44]提出一种信息论结合粒子群算法(PSO)的结构学习方法,将约束最大信息熵作为评分函数,对网络结构进行复杂度约束,并设计了粒子位置和速度向量的操作方法来解决单纯利用KL距离进行搜索的不足。实验证明,在网络结构搜索空间相对较大的情况下,该算法能在较短的时间内收敛,获得更准确的网络结构。2019年,文献[45]利用MI和CI测试构建大尺度约束,在结构迭代优化过程中加入改进GA的小尺度约束,提出基于双尺度约束的BN结构自适应学习算法。实验证明该算法在无先验信息时仍具有良好的学习精度和收敛速度。
2.4 基于节点序搜索的结构学习
2001年,文献[46]提出一种基于K2SN和蚁群算法相结合的节点序搜索算法Ant+K2SN。其中,K2SN算法是改进的K2算法,该算法克服K2算法需要节点序的问题,虽然可以自动确定节点序,但实际生成的节点序与标准节点序不一致,最终会影响BN结构的准确性。2003年,文献[47]提出了一种基于MCMC的方法,该算法的核心是利用MHS抽样算法保证抽样得到的节点序服从后验概率,从而使该算法具有良好的学习精度。但缺点是抽样过程融合性差,收敛速度慢。文献[48]将MHS抽样算法首次引入到贝叶斯网络的结构学习,将局部边的增加、删除和反向的均匀分布作为抽样过程的建议分布,用抽样过程收敛之后产生的平稳分布的网络结构样本来学习贝叶斯网络的结构。但该方法的收敛速度较慢,针对此问题,文献[49]提出PopMCMC算法通过使用来自多个MHS的统计信息来改善收敛速度。2007年,文献[50]提出一种基于节点序的贪婪搜索算法OMRMRG,通过最大关联性和最小冗余特征选择挑选出与目标节点具有高相关性的节点集,并根据BIC公式和过拟合的似然属性提出局部贝叶斯增量函数。实验结果表明,在有限数据集上,OMRMRG算法比上述的BN学习算法具有更高的效率和准确性。2011年,文献[51]针对贝叶斯分类器提出了一种基于最小角度回归(Least Angle Regression,LARS)的结构学习算法L1-BNC。首先利用LARS算法确定节点序,随后用K2算法确定网络结构。文献[52]通过结合LARS算法和MMPC算法获得最佳节点序。相较于其它分类算法,L1-BNC具有更高的效率和精度。2013年,文献[53]提出GES算法,在BN网络结构的等价类空间中进行局部搜索。2017年,文献[54]提出利用最大生成树算法(Maximum Weight Spanning Tree,MWST)和ACO算法获得节点序,再利用K2算法得到最优结构的MWST-ACO-K2算法。该算法解决了ACO算法搜索空间大和K2算法依赖先验的问题。2018年,文献[55]引入基于本地搜索的元启发式方法对GES进行改进,并证实该算法可应用于100个节点的网络中。文献[56]通过改进抽样策略,用与熵成比例的方式对排序变量进行采样,从而覆盖节点序搜索空间,达到提高性能的目的,并可将该算法应用于基于排序空间上的任何算法。文献[57]为进一步提高基于节点序的搜索方法的准确性,运用搜索运算符增加搜索空间从而避免陷入局部最优的问题,并将路径先验作为约束添加到交换过程中来解决由于搜索空间增加而导致效率降低的问题。实验表明,该算法可以取得较准确的结果。
2019年,文献[58]提出利用基于互信息和熵的方法寻找节点序,极大提高了BN网络推理精度。2020年,文献[59]提出将先验知识作为约束条件,并使用MMPC算法将约束添加到OS+算法中。实验结果表明,该算法在保持较高效率的同时,可以产生更好的BN结构。文献[60]提出通过定向支撑树得到节点块序列,再利用BIC评分得到的节点序作为K2算法输入的NCSC算法。实验证明,该算法在精度和运行速度上都有所提高。
2.5 精确算法
近似结构学习算法,只能找出局部最优解或接近于最优的网络结构,并不能保证得到最优解。由于对于n个变量的任何固定排序,分数的可分解性使得与该排序兼容的所有DAG都能进行有效的优化,于是结构学习的精确学习方法应运而生。精确算法可以分为:整数线性规划(Integer Linear Programming,ILP)、A*算法和动态规划(Dynamic Programming,DP)。
2.5.1 整数线性规划算法
ILP算法框架的核心的是分支定界(Branch and Bound,BB),以及增加其效率的各种方法,例如割平面方法,通过引入切割平面来中断循环,直到找到最佳解。分支定界的核心思想是把BN结构学习问题分解为求解一个个的线性规划(LP)问题,并在求解的过程中实时追踪原问题的上界(最优可行解)和下界(最优线性松弛解)。割平面法又称为Gomory割平面法,核心思想是把原问题当做线性规划问题,然后利用切割平面割去可行域中非整数的部分,并循环进行该过程,直到可以直接通过线性规划求出一个整数解为止,此时所求出的整数解就是原问题的最优解。如图4所示,Ρ为约束形成的凸包(可行域)。
图4 线性规划算法图解Fig.4 Graphical illustration of linear programming algorithm
2009年,文献[61]提出基于分支和边界的方法,通过忽略非周期性约束(Acyclic cuts)找到单个变量的最优父集,再通过破坏所有循环以找到有效的贝叶斯网络。实验证明该方法能够处理最多100个变量的数据集。2011年,文献[62]提出一种改进的分支定界算法,采用伪费用分支策略进行问题划分,并利用深度优先搜索(Depth First Search,DFS)策略选择子问题进行扩展。实验表明,该算法能够有效提高求解效率,当n较大时,提升效果尤为明显。2015年,文献[63]提出了一种新型分支定界算法,使用一种新的线性松弛定下界方法和一种超矩形缩减技术来提高算法的逼近程度和收敛速度。实验表明,该算法可以用于处理中大规模的数据集问题。
2010年,文献[64]提出线性整数编程方法(ILP),采用ILP的分支切线思想,并用GOBNILP软件进行了算法实现。2011年,文献[65]提出将非循环性约束以切割平面的形式添加到整数编程(IP)中,使用子IP实现对此类切割平面的搜索。结果表明,该算法可以得到最优的BN结构,程序使用SCIP框架,可由该网址进行复现:http://www.cs.york.ac.uk/~jc/research/uai11。2013年,文献[66]提出一种具有“超结构”的贝叶斯网络学习算法,该方法可找到具有固定树宽得分最高的BN网络。缺点是n<16时,算法复杂度成倍增加。2014年,文献[67]采用整数编程方法,制定切割平面以强制执行树宽约束,被证实可处理多达200个变量的数据集。2017年,文献[68]提出通过增加不必要的隐含约束,可以显着提高性能和结构学习速度,并探讨了如何最好地生成和添加这些隐含约束。程序网址:http://www.cs.york.ac.uk/aig/sw/gobnilp。2020年,文献[69]提出一个提前停止准则,以终止分支定界过程,来获得混合整数编程的最佳解。实验的数值结果证明了该方法的有效性。文献[70]基于有向无环图的汇聚节点的思想,开发了一种启发式算法,并用Python软件编程验证了该算法的效果,实验证明该算法可以找到最优BN网络结构。
基于LP的BN结构学习的关键问题是优化求解器无法应用到具有大量变量的域,即使在线生成约束,该类算法在变量数量上也有指数级的约束,限制了算法的可伸缩性。其中,优化求解器包括IBM Cplex、Gurobi、FICO Xpress、SCIP等,前两个可以免费申请使用且性能较好。当处理样本为81个,SCIP与现有MIP解算器的速度对比如图5所示。

图5 SCIP上不同ILP解算器的速度比较Fig.5 Comparison of different ILP solvers from SCIP
2.5.2 A*算法
A*算法将BN结构学习问题表述为最短路径发现问题。图1显示了四个变量的隐式节点序搜索图。开始搜索节点集合为空,最底层节点集合为目标节点,且每个变量只从上级的变量中选择父集,所有可能路径中的最短路径对应于全局最优贝叶斯网络。其中,评分函数采用MDL。

表3 基于LP的BN结构学习算法总结Tab.3 LP-based BN structure learning algorithm summary
设U为节点序图中的一个节点,其启发式值为

(4)
图中从U到U∩{X}的一段弧线表示通过在已有变量集U上增加一个新变量{X}来生成后继节点;弧的成本等于从U中为X选择父集的成本,通过考虑U的所有子集来计算,即
(5)
2012年,文献[71-73]提出基于最短路径启发式搜索思想,将学习目标表述为最短路径问题,提出A*算法与AWA*算法 (Any-time Window A*Algorithm)。在一致启发式算法的指导下,该算法通过对节点序图空间的修剪来搜索最有希望的解。已被证实在多达26个变量的数据集上表现优于其他算法。2014年,文献[74]提出A$^*$搜索算法,仅通过搜索节点序空间中最有希望的部分空间来学习最佳贝叶斯网络结构。结果表明,该算法是学习最佳贝叶斯网络结构的有效方法。文献[75]提出一种A*lasso的单阶段方法,该方法通过在其评分系统中使用lasso的A*搜索算法来解决单个优化问题,最终恢复最佳稀疏贝叶斯网络结构。图7为变量X1的父节点图修剪过程示例。如果父集合的任何一个前置集合有相等或更高的分数,则该父集合被修剪,修剪后的父集合以灰色显示。

图6 四个变量的节点序搜索图Fig.6 Node order search graph of four variables

图7 变量X1的父节点图修剪过程示例Fig.7 An example of the pruning process of the parent node graph of the variable X1
A*算法根据节点的h值来扩展节点,h值比最佳网络差的子网永远不会生成或留在open list中,即从不扩展不能构成最优完整结构的子网络,这种操作降低了A*算法的内存复杂性和时间复杂性。
2.5.3 动态规划算法
动态规划算法将搜索最优贝叶斯网络问题层层分解为寻找最优子网,用递归公式穷尽搜索节点序空间和候选父集空间,通过牺牲存储量和运行时间,从而保证在不多于26个节点的网络中找到最优网络。该算法要求BN结构至少有一个叶节点,且所用的评分函数是可分解的,其状态转移方程为如下所示:

(6)
bestscore(X,VX)=maxScore(X,VX)
(7)
式中:V为变量集合;X为最优结构中的一个叶节点。在无任何约束的情况下,DP算法的时间复杂度与空间复杂度均为O(n2n),这种复杂性将该算法的实际应用限制在较小的领域。
2004年,文献[76]提出一种基于节点序的动态规划算法(DPBNO),该算法利用先验的节点序修剪搜索空间,从而减少了算法的时耗,但缺点是需要人为给定父节点数量的上限和节点序。2005年,文献[77]提出一种基于深度优先搜索策略的动态规划算法(DFSDP),该算法的优点是可以方便的执行修剪操作以减小存储空间,缺点是计算效率太低。2006年,文献[78]提出SMDP算法,该算法不仅运行时间短,而且可计算的网络规模大。但分层的正确性会影响该算法的精度。2011年,文献[79]提出MEDP算法,利用评分函数的性质对父节点数量上限进行约束,使父节点数量上限n-1减少至m=log(2N/logN)(N为样本量),并采用按层存储与计算的方式进行动态规划,从而再次提高算法效率。但仅仅少量地减少了评分计算次数,约束条件不强。由此引发了添加何种约束对DP算法进行改进的研究热潮。
2018年,文献[80]提出一种融合先验的动态规划结构学习算法(PBDP),引入边约束和路径约束对动态规划算法进行限制,极大的缩小搜索空间。该算法可以确保最优结构符合先验,但结果受先验正确性的影响极大。2019年,文献[81]在DP的基础上,使用IAMB算法得到节点的马尔科夫毯对评分计算过程进行约束,减少评分的计算次数,提出基于马尔科夫毯约束的动态规划算法(DPCMB)。该算法可以在保证算法精度的同时,极大减少算法的运行时间、评分计算次数和所需存储空间,缺点是受限于重要性阈值ε的设置。文献[82]利用条件独立性进行节点分层,并认为每个节点的父节点只来自本节点层和优先级更高的层,结合分层思想和DP,提出分层最优BN结构学习算法(LOL)。该算法也可以减少算法道德时耗,但是依赖于CI检测的正确性。2020年,文献[83]针对DP算法只能应用在小网络的问题,提出利用改进的K均值算法进行网络分块,再利用DP算法对每一块进行学习,最终组合得到最优网络结构的算法(OS-IKM),解决了DP算法无法在合理时间内得到大网络可行解的问题。
表4所示对上述算法进行归纳总结,发现现有算法都是通过增加约束来减少DP算法的运行时间和存储量,但都因为所加约束的强度大小会不同程度的影响算法的精度,因此如何在保证算法精度的前提下,引入约束来提升DP算法效率值得研究。
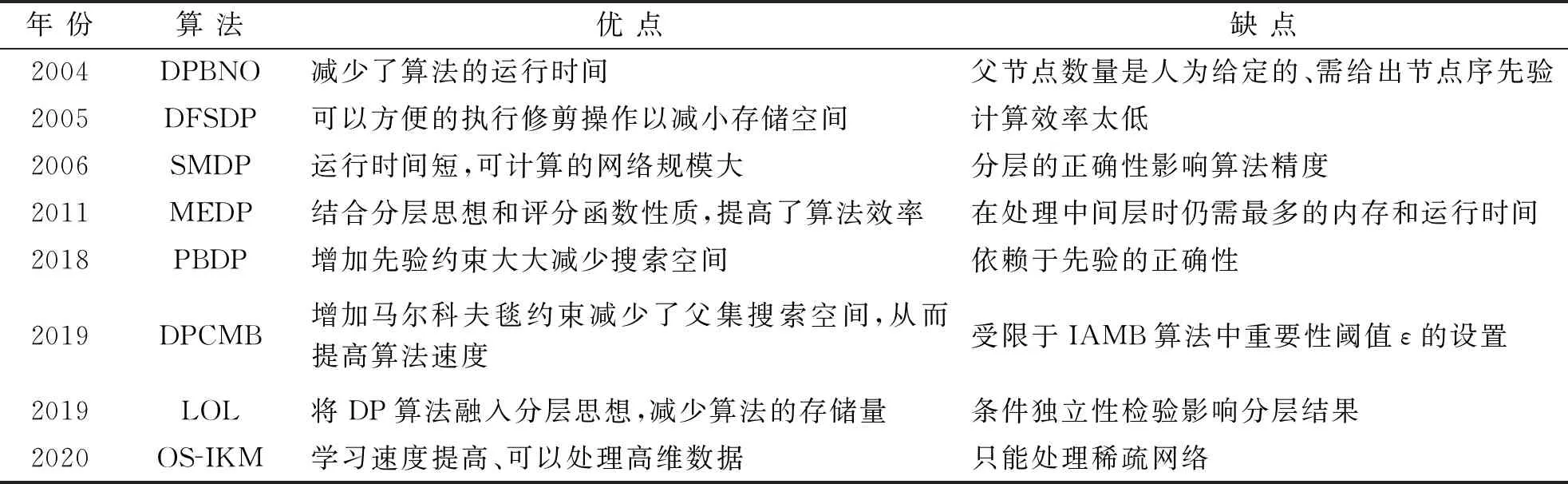
表4 基于DP的BN结构学习算法总结Tab.4 DP-based BN structure learning algorithm summary
3 不完备数据下的BN结构学习
BN结构学习方法都要求数据是完备的。数据不完备会导致两个问题:① 评分函数不再具有可分解形式,不能进行局部搜索;② 部分统计因子不存在,无法直接对网络结构打分。
针对不完备数据集的情况,最经典的BN结构学习算法是结构期望最大化算法(Structural Expectation Maximization Algorithm,SEM)[84]。该方法执行一个两步的迭代过程:① E步:计算当前数据集的统计量,并使用当前的贝叶斯网络中的期望值或模型补全数据;② M步:利用补全的数据集执行BN结构学习算法,一直持续到收敛为止。
MS-EM算法是在EM 算法完成数据修补后,利用爬山算法来寻找最优的网络结构,但爬山算法的计算复杂度较高,针对此问题,提出GES-EMMWST-EM算法;爬山算法也容易陷入局部最优,提出BN-GS算法,把Gibbs sampling和数据集修正与贝叶斯网络结构调整结合在一起。Gibbs sampling过程的收敛性保证贝叶斯网络结构序列的收敛性,依据联合概率的分解独立地对样本进行抽样提高抽样效率。但在保证精度的同时,该算法存在重复计算网络结构的问题,学习复杂度高。上述基于EM算法框架的结构学习算法,计算复杂度高,而且由于网络参数的最大似然估计和数据采样的不准确性使学习准确度较低,只能应用在小范围内。
文献[85]提出在EM算法的最大化步骤中采用k-MAX算法,从而获得对统计量的有效计算,并与基于随机森林的方法进行比较,实验证明该方法可以达到与基于随机森林的方法的相同估算精度,但时间缩短了90%,解决了SEM算法的学习复杂性问题,使其应用范围可以扩展到成千上万个变量。文献[86]使用数据增强方法从缺值的数据中学习贝叶斯网络,将问题重铸为标准贝叶斯网络结构学习问题。该算法的缺点是成本与丢失数据的大小呈指数级关系,仅可应用于小型数据集。文献[87]利用基于截断指数的混合来诱导网络的联合分布[88],依赖数据增强算法迭代地重新估计贝叶斯网络模型。实验证明可应用在16个变量的数据集中。文献[89]给出了节点平均似然性算法(NAL)一般充分条件,并证明了条件高斯BN的一致性和可识别性,以及该算法相对于EM的高效性。
4 仿真实验
本文在Windows 10 64 bit 操作系统,Matlab R2014b软件环境下,基于贝叶斯工具箱FullBNT-1.0.7[90],利用标准Asia网络和Weather网络[91]对常用算法进行了仿真及性能分析。
4.1 近似算法
由图8所示是7种近似BN结构学习算法应用在Asia网络上的BIC评分对比图,包括PC,K2,K2+T,MCMC,GS,GES,SEM。其中,PC算法能够给出较好的学习结果,BIC评分最高;K2算法的学习速度快,缺点是对节点序的顺序非常敏感,图中采用的节点序为ELBXASDT;K2+T算法是利用定向支撑树获得的节点序作为K2算法的输入进行BN结构学习,由于定向的正确性较低,BIC评分较低;MCMC算法是利用模拟退火算法搜寻所有的DAG空间,对数据量的大小并不敏感;GS算法以MWST树为初始图时,该算法对数据长度变化具有更强的鲁棒性;GES算法在数据量较大的情况下,生成的网络比传统的GS算法得到的网络BIC得分更高;SEM算法得到的BIC评分最低。
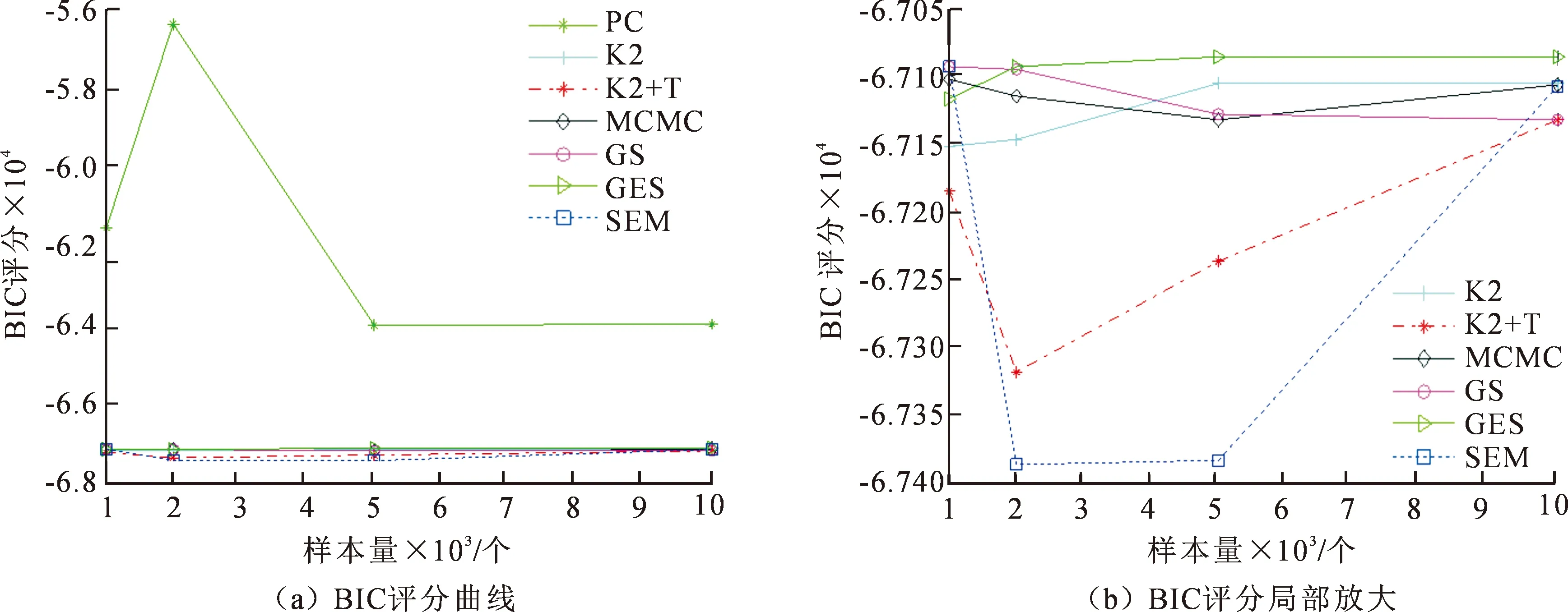
图8 近似结构学习算法的BIC评分对比图Fig.8 Comparison chart of BIC scores of approximate structure learning algorithms
4.2 精确算法
如图9所示,比较了ILP算法增加约束后的运行时间,实验一增加了聚类切割、非循环切割和Gomory分数切割,实验二增加了聚类切割和Gomory分数切割,实验三增加了聚类切割和循环切割,通过上述比较可以发现三种约束中,非循环约束是最重要的,即非循环切割是降低ILP算法复杂度的关键。
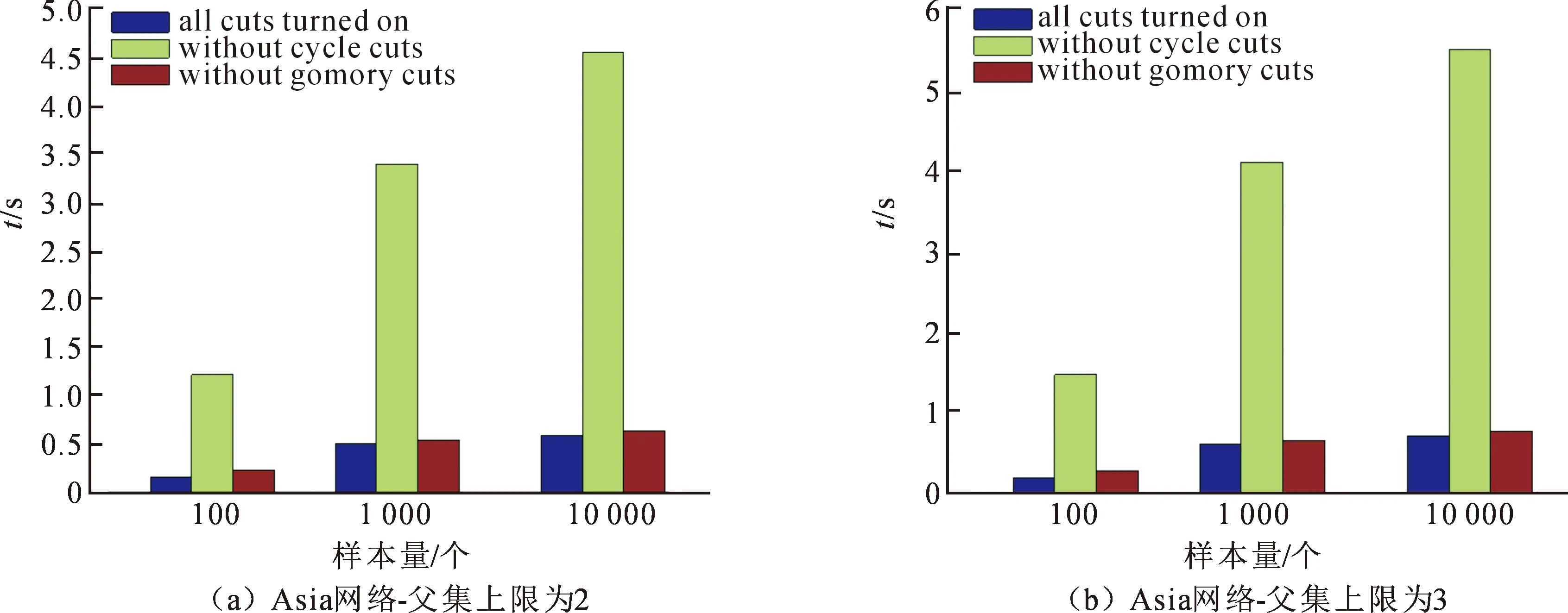
图9 增加不同约束的ILP算法的运行时间对比图Fig.9 Comparison of running time of ILP algorithms with different constraints
由图10所示是4种改进的DP算法的运行时间对比图,包括DFSDP(基于深度搜索的DP算法)、BFSDP(基于广度搜索的DP算法)、CBDP(基于依赖性约束的DP算法)和PBDP(基于深度搜索的DP算法),其中,BFSDP和PBDP的运行时间相对较短,DFSDP的运行时间最长。

图10 DP算法的运行时间对比图Fig.10 Comparison of running time of DP algorithms
5 结 语
1) 从近似算法角度看,可以研究能够处理大量数据并在分布式计算环境中运行的可伸缩式算法,或研究将用于父集识别的BIC*的过程扩展到贝叶斯网络的其他评分函数(例如BDeu分数),或引入新的启发式算法进行寻优,或提出一种新型的评分函数。
2) 从精确算法角度看,DP和ILP方法值得更深层次的研究。针对动态编程,可以考虑加入约束来减少搜索空间,提高算法效率,或研究将IAMB算法中的阈值设置为自适应阈值,提高约束的质量。针对整数规划,可以考虑继续改进分支定界算法,减少运行时间或寻找更好的切平面来增强限制。
3) 针对不完备数据的结构学习,研究如何对EM算法框架进行改进,或提出一种新型的数据采样算法来提高采样数据的准确性,或考虑直接进行多次的数据插值,或研究在不进行数据填充时,是否可以直接进行BN结构学习。
4) 针对小数据集条件下,研究如何充分利用先验和专家信息进行结构学习,并对错误的先验信息具有一定的容错性。
5) 针对大型网络的结构学习,研究如何利用次优结构集,选择合适的模型平均方法从而得到最优结构;研究在保证得到最优网络结构的前提下,如何进行结构分解和结构组合;
6) 针对BN输入为不同量纲的信息时,研究如何处理不同量纲的信息,进行建模和结构学习。例如在故障预测中,输入为数据和图片信息时,如何处理这两个完全不同量纲的信息。
