一种红外测温的误差建模与补偿方法*

王军帅，田军委，张 杰，苏 宇

(1.西安工业大学 兵器科学与技术学院，西安 710021；2.西安工业大学 机电工程学院，西安 710021；3.内蒙古北方重工业集团有限公司，包头 014033)

在需要精确地测量特定区域目标的温度的情况下，与传统的测温技术相比红外热像仪测温技术有很多优点，例如具有非接触性、测温距离远、灵敏度高、速度快，以及可以在图像中选取被测目标等许多优点[1-3]。广泛应用于电力，医学，生物，矿业等诸多行业[4-7]。然而影响红外测温精度的因素有多方面，包括不同物体表面发射率，环境温度，以及测温目标距离[8-9]。而其中主要的影响因素便是测温目标距离。

为了验证距离对红外测温效果的影响，文献[10]研究发现在近距离测温时，最大误差可达±5 ℃；在远距离测温时，误差在±0.02 ℃范围之内，研究了距离范围对测温的影响，没有确切得出距离和温度的关系模型。文献[11]研究得到测温距离在40～112 cm范围内的平均测温精度是0.43 ℃，未提出相应的函数关系来指导温度补偿。文献[12]针对不同的两个热源温度，得到了20 m范围内的测温值与真实值之间的变化关系，提出了温度-距离的分段数学模型并对测温数据进行误差补偿，在较远距离下有明显效果，在较近距离范围尤其是1 m以内并不适用。文献[13]研究了目标距离以及视场角变化对红外热像仪测温精度影响，推导出了红外热像仪测温精度与目标距离和视场角之间的关系式，计算了温度测量误差，测量误差仅为-0.22 ℃，此温度测量精度误差仍然较大。

本文针对固定环境下电路板各部分温度测量的应用需求，在1 m测温距离内，以红外目标辐射理论为基础，研究热像仪测温时距离变化对测温精度的影响。对不同测量距离下的测温数据在Matlab进行拟合分析，得出不同距离下温度补偿的数学模型。

1 红外热像仪测温原理

自然界一切温度高于绝对零度的物体，由于分子的热运动，都在不停地向周围空间辐射包括红外波段在内的电磁波，通过对物体自身辐射的红外能量的测量，便能准确地测定它的表面温度，辐射测量过程如图1所示。

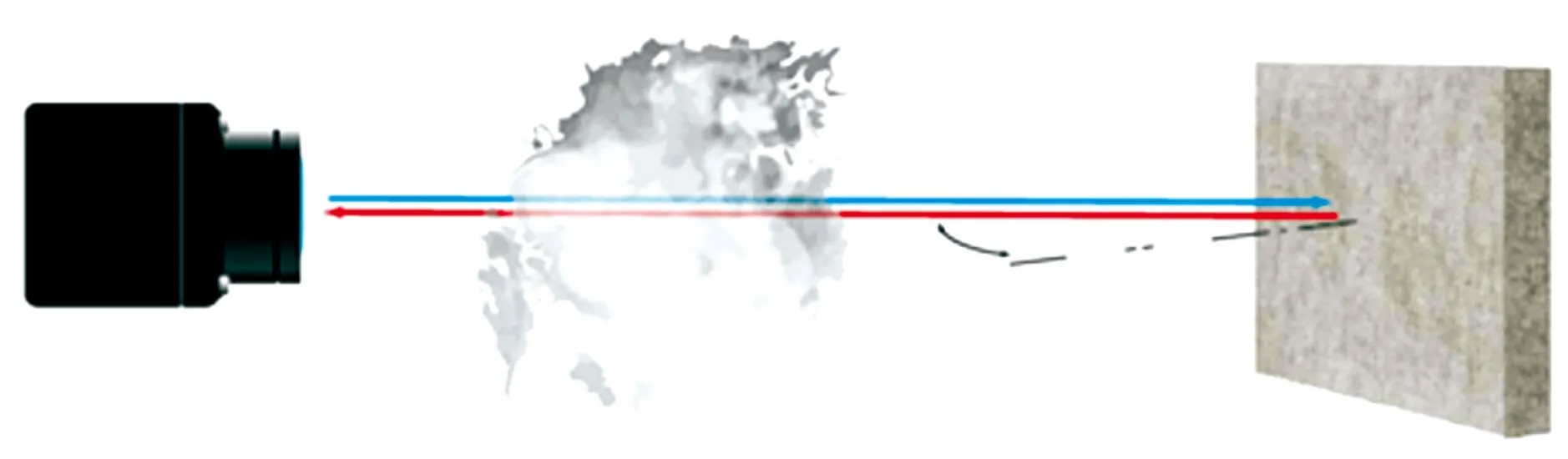
图1 辐射测量示意图Fig.1 Radiation measurement diagram

普朗克辐射定律揭示了黑体辐射能量在不同的温度下按波长分布的规律，是红外测温技术的理论基础，其表达式为

(1)

式中：Eb,λ为黑体光谱辐射能量密度；c1为第一辐射常数，c1=3.741×10-16W·cm2；c2为第二辐射常数，c2=1.438 8×10-2W·K；λ为光谱辐射的波长。

Stefan-Boltzmann定律指出,黑体的辐射能量随着温度的增加呈现出非线性变化,且一个黑体表面单位面积在单位时间内辐射出的总功率和黑体本身的热力学温度的四次方成正比,表达式[14]为

(2)

式中：T0为被测物体表面温度；Tr为热像仪指示的辐射温度；Tu为热像仪温度；Tα为环境温度；ελ为表面发射率；αλ为表面吸收率；ταλ为环境的光谱透射率。

由式(2)中可以看出，在被测目标物体的发射率、吸收率和测量时的视场角一定，环境中无高温热源影响的情况下，影响热像仪测温精度的因素有环境温度、环境湿度以及测量距离。以上3个要素的变化均会对热像仪测温产生影响。在相同条件下，改变其中任何一种因素的值，均会使热像仪测量温度值发生变化，但在实验过程中发现，在环境湿度和环境温度一定的情况下，当改变距离的同时，如果重新进行热像仪标定，能够很大程度上降低环境因素对热像仪的测温精度的影响。

2 距离对红外热像仪测温的影响

2.1 理论分析

实际测温时，红外热像仪接收到的有效红外辐射包括目标自身辐射、环境反射辐射以及大气辐射三部分。假设大气路径的瞬时辐照度对背景和物体的影响相同，且大气透过率在探测光谱波段为常数，对于灰体而言，红外热像仪对被测物体的作用距离[12]为

(3)

式中：μ为大气消光系数；ΔE为探测器接收到的辐射对比度；a1，a2为常数，由热仪工作波段确定，σ为Stefan-Boltzmann常数，ελ，εu为物体和背景的表面发射率。

对式(3)两边进行微分,可整理得：

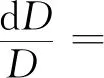
(4)

其中H=(T0/Tu)4。

根据式(4)可知，红外热像仪对被测物体的作用距离的测温误差与物体的表面发射率及表面温度测量误差、背景温度测量误差以及大气消光系数的测量误差有关。所以实际应用中，需要对所测温度值进行补偿以提高精度。

在实际测量得到温度数据时，得到实际测量误差：

e=Tr-T0，

(5)

通过对实际误差进行拟合，可以得到误差拟合曲线e′

e′=f′(D)，

(6)

其中f'(D)=(Tr-T0)′。根据式(4)推导结果，可猜测误差模型e′为

(7)

(8)

则，补偿后温度T′为

T′=T0+e′。

(9)

2.2 实 验

在一定温度下对不同测温距离的精度研究。实验研究不同测温距离的测温精度，测温距离为110 cm，以10 cm为间隔，往返测量5次以求取平均值减小测量误差。黑体温度设置为40 ℃。该实验是在实验室内进行，环境条件相对比较理想，视场角不变，环境中无高温热源的影响，仅改变距离。在实验过程中，要将热像仪进行充分预热，使热像仪保持热稳定。如图2(a)为Lepton 3.5非制冷红外热像仪和OpenMV开发扩展板；如图2(b)所示为上海芸尖智能科技有限公司测温黑体HT-C50,温度范围0～60 ℃。实验在固定的实验室内部环境下完成，在测量的过程中，环境温度16 ℃，湿度34%。

图2 OpenMV 硬件开发板与黑体Fig.2 OpenMV hardware development board and Blackbody

实验步骤：先布置热源，保持其真实温度为40 ℃。以米尺作为量距仪器，测温间隔为10 cm，总距离为110 cm。启动红外热像仪软件，预热传感器，系统自动校正红外探测器的不均匀像素。调节红外热像仪程序参数，设置灰度区间、最高和最低温度等参数。设置不同的距离，待红外热像仪稳定后，垂直对准被测目标进行测温，不同距离处测温10次，取平均值以减小测量误差和人为操作仪器的影响。以10 cm为间距，从10 cm至110 cm往复测量5次，记录数据。实测温度数据见表1。

表1 实际测得温度数据Tab.1 Measured temperature data 单位:℃

续表1

3 实验结果分析

3.1 实验结果

表1给出了10组在10～110 cm距离下测量得到的温度数据。从所得的数据可以看出，测得数据值的误差随着距离增大而增大，为保证在一定距离下的测温精度，须对所得的数据进行校准。

3.2 实验分析

为了更直观的观察数据，利用Matlab对表1中的数据画出折线图，如图3所示。

图3 实际测量温度-距离图Fig.3 Measured temperature-distance diagram

由图3可知，多次测量结果有着相似的变化趋势，证明实验结果是有效且存在一定的变化规律。从10 cm处测量开始，测量结果略高于实际温度，随着距离的增加，所测得温度逐渐降低。在测量距离为80 cm时测得温度波动明显，主要是由于测量距离较远所导致。

由图4可以看出，在近距离时，由于目标充满测量仪视野，所测温度接近目标实际温度；随着距离的增加，误差变化明显，在30～70 cm距离范围所测得温度趋于稳定；在距离较远时，目标温度变化明显。因此，为了保证红外测温值的有效性，必须通过一定的温度补偿方式来补偿距离对红外测温的影响，以提高红外测温精度。

图4 平均温度误差-距离关系图Fig.4 Average temperature error-distance diagram

利用Matlab对表1中的数据进行拟合，得出了40 ℃时的距离与平均温度拟合函数及相关系数。

指数拟合(Exponential fitting，Exp)

y=-1008exp(-0.01342x-0.7877)+1006，

R2=0.7229。

(10)

多项式拟合(Polynomial fitting,Ploy)

y=(6.719e-08)x4-(2.487e-05)x3+

0.002959x2-0.1461x+1.744，

R2=0.7988。

(11)

由图4可以看出，在10～80 cm有着连续变化趋势，90～110 cm处变化波动明显，在温度变化速率不同的各阶段，温度的变化不能用单一的模型来衡量，应该对所测温度进行不同程度的温度补偿，故提出了温度-距离分段补偿模型。建立温度-距离补偿模型，得到40 ℃温度-距离补偿模型：

(12)

式中：y为补偿后温度；y0为红外测温值；x为测温距离。

通过温度-距离补偿模型对所测红外温度值进行分段补偿，计算分段补偿后温度值与真实温度值的差值，并计算相对误差和均方根误差来评价补偿模型的质量，见表2。

表2 温度分段补偿表Tab.2 Temperature subsection compensation

根据指数拟合，多项式拟合，以及温度-距离分段补偿模型分别对测得温度进行补偿，结果如图5所示。

图5 三种补偿效果误差图Fig.5 Error diagram of three compensation effects

由图5可以看出3种补偿模型得到的误差效果。指数模型补偿结果整体超过实际温度；多项式模型补偿结果波动明显；分段模型补偿结果整体效果好于指数模型和多项式模型补偿结果。因此，温度-距离分段补偿模型效果最好，实际采用温度-距离分段补偿模型作为温度补偿方式。

由表2可知，温度-距离补偿模型对红外测温误差具有较好的补偿作用，温度为40 ℃的热源红外测温值相对误差最大为3.73%，经过温度-距离补偿模型校正后，最大相对误差为0.87%，均方根误差为0.604 1。由此可见，文中提出的温度-距离模型对由距离引起的红外测温误差具有较好的补偿作用能够有效提高测温精度。

4 结 论

文中研究了测温距离对红外测温精度的影响，近距离时目标充满测量仪视野，所测温度接近目标实际温度；随着距离的增加，温度误差变化明显。通过对实验获取的测温数据进行拟合分析，得到温度-距离拟合关系。根据红外测温数据与距离的关系，提出了温度-距离分段补偿模型，通过该模型补偿后的温度最大相对误差仅为0.87%。该温度补偿模型对红外测温的精度补偿具有重要作用。