瓜瓣模上定位销孔的改进加工工艺

张大勇 赵文利 尉晓霞 刘继军 孙勇跃

（首都航天机械有限公司，北京 100076）

文 摘 针对瓜瓣阳模上定位销孔加工的找正误差大、实物与数模不一致、加工成本高的难题，通过改进找正方法，粗、精找正结合，并利用3D寻边器进行程序验证的思路，实现了理论数模和实物的精确对齐、找正。在此基础上通过椭球参数方程的坐标转换，实现了在3轴机床上对椭球面上法向和轴向定位销孔的加工。结果表明，采用改进后的加工方法，孔的位置精度达到Φ0.1 mm，加工成本降低75%，可在工程应用中加以推广。

0 引言

运载火箭推进剂贮箱的箱底形状通常为椭球曲面，其制造路径主要是先成形出瓜瓣件，再拼焊成整体箱底［1］。瓜瓣模是钣金类瓜瓣产品成形模具，零件成型过程是首先在压力机上在固定好的板料上方压下一段距离，使板料逐渐贴合模具成形，实现板料的拉形成形过程［2］。瓜瓣上的定位销孔分为两种：一种是对钣金零件在阳模上进行定位；另一种是检测销孔，结合检测芯棒用于对钣金产品上的开孔尺寸进行检测。两者的加工精度直接影响瓜瓣产品的尺寸精度。

由于大多数瓜瓣模在20世纪80年代制造，对其返修时存在与过去找正基准不统一、实物模型与理论数模不一致的困难，导致新增定位销孔的加工误差很大，难以满足使用要求。此外，类似椭球面上的定位销孔过去一直采用五轴机床加工，高昂的加工成本也是企业经营者面临的重要问题。

为了提高瓜瓣模上定位销孔的加工精度、降低加工设备对于五轴机床的依赖，本文通过改进找正方法，消除找正误差，在建立实物与理论数模联系的基础上，并通过坐标转换计算实现在三轴机床上对椭球面上定位销孔的加工，最终达到提高定位销孔加工精度、降低加工成本的目的。

1 瓜瓣模阳模特点和加工难点

1.1 阳模特点

成形阳模型面为椭球面，三维模型见图1。阳模材料为铸铁QT500，型面上定位销孔直径mm，有效深度15 mm。

椭球方程为：

式中，a为椭球长半轴半径，b为短半轴半径，y轴为回转轴。极坐标表示见图2。

图1 阳模三维模型Fig.1 Three-dimensional model of melon mold

图2 椭球极坐标参数模型Fig.2 Ellipsoid polar coordinate parameter model

A为椭球面上任意一点，图中r代表点A绕y轴的回转半径，r=ρ·sinβ，点A的极坐标表示的参数方程［3］为：

如图3所示，阳模底面与椭球回转轴呈φ角，椭球形面上新增5 处定位销孔，其中孔1 轴线与椭球回转轴y轴平行，其余4 个孔轴线为球面上法线的方向。5 个孔分布在半径r0、r1、r2的圆周上，L0为r0对应的孔距模具底面的高度。

图3 椭球二维草图截面和E向孔的分布Fig.3 The two-dimensional sketch of the ellipsoid cross section and distribution of holes in E

1.2 加工难点

1.2.1 找正误差大、基准验证困难

图1所示阳模外形为铸造成型，并未二次加工，型面上也无明确的基准面和基准孔供找正用。椭球形面上的零件边缘线是唯一可用作找正的基准，而零件边缘线本身的宽度约0.2 mm，普通的2D 寻边器、杠杆百分表等找正工具只适合二维拉伸和圆柱外形的找正，无法利用线或者三维曲面找正。探针虽然可以用在零件边缘线的找正，但探针的尖制造误差通常在0.05 mm 左右，因此，探针和零件边缘线自身误差的累积会导致较大的基准找正误差，导致定位销孔的加工超差。

再找正完成后，验证找正基准的准确性成为一大难题。如果生成加工程序用刀具验证，极有可能损伤零件表面。因此，找到合适的验证工具成为关键。

1.2.2 实物与理论数模的数据匹配误差

瓜瓣模具阳模型面过去多采用仿形铣半精加工、型面样板修配的方式进行，虽然椭球面的自身轮廓度能控制在0.10～0.15 mm，但由于当时没有先进的数控机床严格控制椭球面与模具底面的相对位置，所以图中L0、φ的实测值和理论值会存在误差，如果定位销孔仍然按理论数模尺寸加工，显然不符合使用要求。

1.2.3 加工成本高

由公式（1）可以推得椭球面上任意一点的法向量为（2x/a2，2y/b2，2z/a2），5 个孔的空间角度均不一样，五轴加工机床虽然能解决孔的加工问题，但是高昂的制造费用是经营者不得不面对的难题。如果能摆脱对于五轴机床的依赖，将会对后续模具的返修带来极大便利。

2 定位销孔的改进工艺设计

2.1 实物与数模y轴的找正对齐

如果采用数控加工，就必须建立理论数模与实物的联系，需要将零件椭球型面位置与数模当中摆放位置完全一致。椭球的理论回转轴为y轴，阳模加工的回转轴为B轴，理论数模中阳模底面与y轴成φ角，在实际加工中需要将阳模底面调整到与工作台面成φ角，见图4。

然后将y轴和B轴重合。椭球面上与xOz平面平行的任意截线为一半径为定值的圆，如果刀轴处于与xOz平面平行的平面内不动，则位于该截面内的圆上任意一点在旋转过程中会与刀轴上的固定点保持同等距离。利用这一原理，将百分表装到刀轴上，表头与工件表面任意一点接触，然后旋转B轴，根据百分表示值变化调整阳模位置，直至百分表指针在B轴旋转任意角度跳动很小，近似认为B轴和y轴重合。

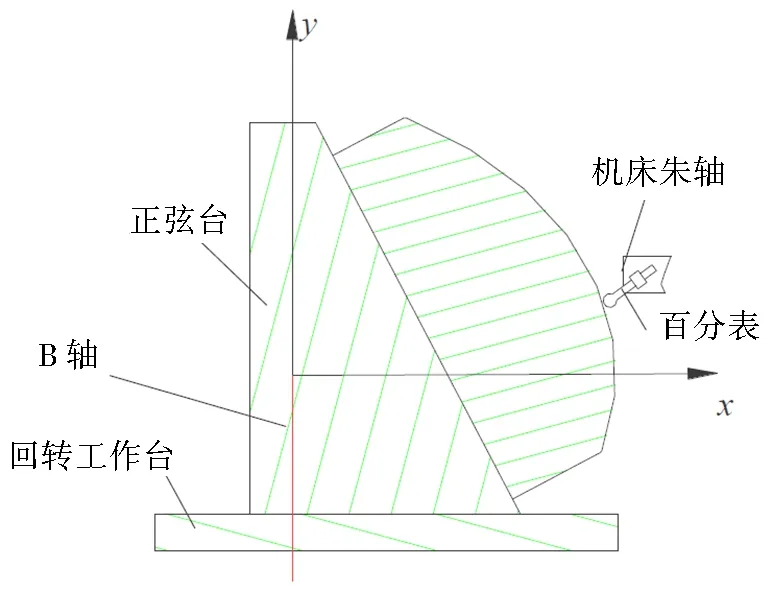
图4 用于调整阳模角度的正弦台Fig.4 Sine table used to adjust the angle of the male mold

在调整的过程中，φ角实际和理论的偏差会对找正结果有很大影响，图5显示在φ角偏差1°时，用上述方法在y=200 截面上找正百分表示数的变化为1113.76-1113.41=0.35 mm。

图5 摆角φ对找正的影响Fig.5 The influence of swing angle φ on alignment

因此，如果在理论角度φ对工件找正存在这个误差时，通过调整正弦台的旋转角度来调整阳模相对B轴的角度至φ′（实际阳模底面与y轴的夹角），以确保百分表示值的变动尽可能小，只有这样，B轴和y轴的重合误差才最小。

2.2 实物与理论数模在xOz平面的找正对齐

实物与理论回转轴对齐之后，只能确定y轴在加工坐标系中的位置，如果保证数模和实物的完全匹配，还需要确定理论xOy平面、xOz平面在实际加工坐标系中的位置。而且由于仿行铣的加工精度决定了2.1节中的坐标轴重合误差依然存在，还需要对φ′角进行精确验证。

由于椭球面为回转曲面，理论上过旋转轴的任意截面均可旋转至z=0 的对称截面（xOy平面）上，确定这个唯一截面是已刻零件边缘线，但是零件边缘线自身存在误差，因此，如果精确对齐，还需要对现有找正方法进行改进。

2.2.1 利用探针粗找正

利用零件边缘线在椭球面上的交点A、B、C、D，使用划针对刀，将实际加工坐标系与椭球理论坐标系粗对齐，直线AB、CD平行于z坐标轴，AB和CD中点E、F的z值均设为零，由于零件边缘线的刻线宽度约为0.2 mm，划针的尖制造误差约0.05 mm，而型面尺寸正确，因此找正误差约0.3 mm。

2.2.2 精确对齐

在数模上找到xOy面内对应的E、F两点，测量线段EF弦长，由于步骤1 的找正误差在0.3 mm 左右，因此，坐标系的对齐误差可以通过分别以E、F两点为圆心半径1 mm 的圆内均匀取10个点，计算得到的EF长度如果与数模当中量得的弦长最接近，理论上此E、F两点的坐标为精确位置。E、F点的实测位置更换为数模中的理论坐标，就将加工坐标系原点移到了理论数模的原点上，保证实物的摆放位置跟数模完全一致。

2.2.3 程序验证

在数模当中沿刀具在z=0 的平面内轨迹为一椭圆轨迹，生成加工加工程序，用图6所示3D 寻边器进行程序验证。将3D 寻边器固定在机床主轴上，主轴中心可以精确地定位在工件的各边上。其优势在于可以从任意方向接近零件，在测量过程中，指针始终沿一个方向偏移，并始终显示机床主轴中心与工件边之间的距离。程序验证过程见图7，刀轴沿x、y方向做差补即可，可以通过其示值的跳动来旋转B轴对摆角、旋转正弦台对φ角进行微调，直至找正误差最小。

图6 3D寻边器Fig.6 3D edge finder

图7 程序验证的方法Fig.7 Program verification method

然后，将E、F两点的实测坐标值替换为理论坐标值，加工原点最终与数模保持一致。

2.3 坐标转换，变五轴加工为三轴加工

对椭球面上任意一个孔M的加工，需要知道其在椭球面上的坐标M（x，y，z）及孔的轴线与各轴的夹角，用方向余弦如公式（3）表示：

当z=0时，cosγ=0，孔的轴线方向余弦就简化为：

经过计算得知：

可见，α′和β′互为余角。加工时，保证刀轴方向与方向余弦一致就可以进行孔的加工。所以实际加工过程中，如果将被加工孔的回转截面绕y轴旋转到xOy面内，就可以实现刀具单一角度对孔的加工。具体方法是，在机床坐标系中，将椭球原点设置为零点，同时数模中的椭球原点坐标值也为（0，0，0），此原点也是加工坐标系原点。如果将实物阳模中被加工孔绕旋转轴回转到xOy平面，将数模当中的模型也绕y轴整体旋转角度α，此时的z坐标为0，α=0，代入公式（2）旋转完成后孔的刀位点信息就变为：

而椭圆的平面方程为：

对于回转半径为r的孔，刀位点和刀轴的倾斜角度表示方法为：

因此，孔的加工在3轴机床上即可完成。

3 加工验证

在3轴机床上进行改进后的加工工艺验证，机床定位精度0.02 mm。定料销孔先用Φ5.9 mm 钻头粗钻，再采用直径Φ（6+0.012）mm三刃立铣刀精加工，转速n=1 500 r/min，轴向进给速度f=10 mm/min，加工验证的具体流程，见图8。

图8 加工流程图Fig.8 Processing flow chart

在调整y轴与机床B轴重合过程中，当φ角尺寸至φ′时，百分表的最小示值变动范围为0～0.15 mm，粗找正误差即0.15 mm。

在φ′角对EF 两点粗找正时，假设EF 两点的理论弦长为a0，实测值为a0+0.2。精确找正时在以E点和F点为圆心，半径为1 mm 的圆内各取10 个点，分别为E1，E2，...，E10和F1，F2，...，F10，在对这20 个点坐标值记录后，计算发现E3F8的弦长与理论值a0最接近，为a0+0.03。以此两点作为程序的找正基准，程序在验证过程中的示值变化范围为0～0.08 mm，继续对φ′角修正至φ″时，示值变化范围为0～0.03 mm，同时旋转B轴，发现3D 寻边器的示值变化由原来的0～0.15 mm 变为0～0.05 mm，认为找正误差满足要求，并重新记录E3和F8的实测值，将理论值替换实测值后，设定加工坐标系原点。

最后，采用此方法加工出来的孔位置度Φ0.1 mm，完全满足设计图纸要求，改进前后孔的位置度和加工成本对比见表1。

表1 改进前后的加工对比Tab.1 Comparison of processing before and after improvement

改进找正和加工方法后，找正误差从0.5 mm 降到0.05 mm，孔的位置度由之前的Φ0.55～Φ0.8 mm提高至Φ0.1 mm，孔的加工成本从原来2 万元降低至0.5 万元，降幅达到75%，改进效果显著。通过表1，可以得出以下结论：

（1）改进找正方法后，找正误差从0.5 mm 降到0.05 mm，主要是由于在零件轮廓度得到精确保证的情况下，采用双重保障，也即结合椭球面的回转特性和3D 寻边器替代刀具程序验证椭球截面方程的方法，尽可能减少找正误差；

（2）孔的位置度由之前的Φ0.55～Φ0.8 mm 提高至Φ0.1 mm，除了找正精度提高之外，还跟理论数模和实际之间的误差得到修正有关，主要是通过正弦台的调整保证了理论型面和实际型面的精确对齐，也即将理论型面的空间坐标系统一到加工坐标系下，就避免了使用实物非型面外形找正引入的误差，因此加工精度有了显著提高；

（3）通过坐标转换推导得到椭球面定位销孔的三轴加工刀位点信息，不再依赖五轴机床加工，五轴机床的每小时加工费用通常约为三轴加工中心的四倍，因此，改进后的加工方法能够降低生产成本75%。

4 结论

针对瓜瓣阳模上定位销孔加工的找正误差大、实物与数模不一致、加工成本高的难题，通过粗、精找正结合，提出用3D 寻边器进行程序验证的思路，改进找正方法，实现了理论数模和实物的精确对齐、找正，并通过椭球参数方程的坐标转换，实现了在3轴机床上对椭球面上法向和轴向定位销孔的加工，孔的位置精度达到Φ0.1 mm，加工成本降低75%，可在工程应用中加以推广应用。