网络拥塞控制模型Hopf分岔的PD控制
2021-04-06侯萍
侯 萍
(南京邮电大学 管理学院,江苏 南京 210003)
0 引 言
网络服务质量是网络应用的重要保障。对网络系统的稳定性和动力学特性的研究具有现实意义[1-7]。网络拥塞控制算法的主要目的是维持系统的稳定性,使信息流趋于特定的稳定值,力求最大的链路容量利用率[8]。一般来说,系统稳定性的丧失随之而来的是阻碍通信发展和链路容量的浪费,其中分岔行为可能引起振荡,诱发网络不稳定,所以需要控制分岔。文献[9]讨论了一种利用状态反馈控制器对网络拥塞控制系统的流体流模型进行Hopf分岔控制的问题。在状态反馈控制下,Hopf分岔的发生被成功地延迟,从而使稳定域得以扩展,通过调整控制器的线性部分和非线性部分的参数来确定分岔周期解的性质。文献[10]研究了由非线性延迟微分方程控制的无线接入网络的Hopf分岔分析,如果延迟超过临界值,闭环系统将不会保持稳定,并且发生Hopf分岔,应用积分滑模控制作为非线性鲁棒主动队列管理控制器来阻止网络拥塞。文献[11]为了控制不理想的Hopf分岔,提出了一种混合控制策略,通过线性稳定性分析,表明适当调整混合控制策略的控制参数,可以在不改变系统平衡点的情况下延迟甚至完全消除Hopf分岔。文献[12]提出了一种具有参数时滞的反馈控制方法,用于控制时滞分数阶双拥塞模型的分岔控制。利用参数时滞反馈控制器可以大大提高系统的稳定性,但在没有控制器的情况下,Hopf分岔会提前产生。
该文针对用于无线网络拥塞控制算法设计的TCP Westwood/AQM流体流模型进行稳定性和Hopf分岔分析,应用中心流形和规范型理论确定Hopf分岔周期解的方向和稳定性,并应用PD控制器控制Hopf分岔,最后给出数值实例及仿真证明算法的有效性。
1 TCP Westwood/AQM拥塞控制系统的Hopf分岔
通常在通信网络的传输层中实现的传输控制协议(TCP)可以检测其发生后的拥塞。但是,由于时变衰落和分组错误率,在具有无线接入链路的网络中,拥塞控制可能更加有挑战。
TCP Westwood是专门为高速无线网络设计的,完全符合高速无线网络的特点,大大提高了网络带宽的利用率,改善了网络性能。同时使用健壮的主动队列管理来防止拥塞,并对无线环境的严重干扰具有一定的容忍度。
文献[13-14]提出了源端采用TCP Westwood拥塞控制协议,路由器端采用随机早期检测算法(RED)的网络系统的流体流模型,在这里假设网络中仅有一条单链路,并且所有的TCP连接都遵循TCP Westwood拥塞控制协议。为控制Hopf分岔来实现一些预期的动力学行为,引入带有一个输入e(t)和一个输出u(t)的PD控制器,表示如下:
(1)
其中,输出偏差信号定义为e(t)=p(t)-p*,kp,kd分别为比例控制参数和微分控制参数。
因此,带有通信时延的受控拥塞控制模型[15]如下:
(2)

系统式(2)在平衡点处线性化,得到:
(3)
其中,y1(t)=W(t)-W0,y2(t)=q(t)-q0。
式(3)的特征方程为:
λ2+mλ+ne-λR=0
(4)
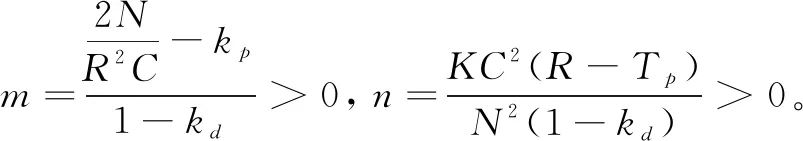
令特征根λ=±iω0,其中ω0>0,代入特征方程式(4),虚部实部分开,则有:
(5)
从中可以看出ω0R0<π/2。
引理1:当往返时间R=R0时,特征方程式(4)有唯一一对纯虚根λ=±iω0,且ω0R0<π/2。
引理2[17]:对于特征方程式(4),如果令M(R)={λ:Re(λ)≥0,Q(λ,R)=0},该式表示使得特征方程Q(λ,R)=0具有非负实部的特征根的个数,设R2>R1≥0,如果对于任意的往返时间R∈[R1,R2],特征方程在虚轴上没有解,则M(R1)=M(R2)。
引理3:当R 证明:当R=0时,特征方程为Q(λ,0)=λ2+mλ+n=0。又因为m>0,n>0,所以Q(λ,0)=0的特征根都有负实部,得到M(0)=0。从上面的分析得到当往返时间R 引理4:当往返时间R=R0,特征方程式(4)除了有一对纯虚根是±iω0外,其他的根都具有严格的负实部。 引理6:当往返时间R=R0,特征方程式(4)至少有一个根具有严格正实部。 基于上述引理分析特征方程的特征根的分布区域,应用文献[18]中的有限时滞微分方程的Hopf分岔定理得到具有PD控制器的拥塞控制系统式(2)的分岔定理,如下所示: 定理1:对于带有通信时延的添加PD控制器的拥塞控制模型式(2)有如下结论: (1)当往返时间R (2)当往返时间R>R0,拥塞控制系统式(2)在平衡点(W0,q0)不稳定; (3)当往返时间R=R0,拥塞控制系统式(2)在平衡点(W0,q0)产生Hopf分岔,出现周期解。 对已线性化的式(3)在平衡点进行泰勒展开,结果如下: (6) 设R=R0+υ,u(t)=(y1(t),y2(t))T,ut(θ)=u(t+θ),θ∈[-R,0]Ck[-R,0],初始条件φ(θ)=(φ1(θ),φ2(θ))T∈C[-R,0],则式(6)表述如下: (7) Lυφ=G1φ(0)+G2φ(-R) (8) F(φ,υ)= (9) 将式(7)转换为下述形式: (10) 对于φ(θ)∈C[-R,0],令: (11) (12) 令q(θ)是A(0)对应于λ(0)的特征函数,即A(0)q(θ)=iω0q(θ)。 对于ψ∈C[0,R],定义伴随算子为A*(0): <ψ,Aφ>= 则有如下引理: 下面计算υ=0时中心流形C0的坐标,该文采用同文献[20]Hassard同样的表示。对于ut当υ=0时,式(10)的解定义为: j(t)= (13) W(t,θ)=ut-jq+jq=ut=2Re{j(t)q(θ)} (14) (15) 对于式(10)的解ut∈C0,根据式(11)~式(13),由于υ=0得: (16) (17) … (18) (19) (20) (21) 在C0上, (22) 将式(15)、式(17)代入式(22)得: (23) 对照式(21)、式(23)系数,得: (24) 因此,得到: 很明显, K1=m13+m14ρ1e-iω0R0 与式(18)比较系数: 为了得到式中的g21,还需要计算出W11(θ)和W20(θ)的值,其中θ∈[-R,0)。根据前面已经得到的式(19),(20),对于θ∈[-R,0)有: 上式跟式(18)比较系数,得: 根据式(24)得: 解方程得: 同理得: 根据文献[13],最后得到: (25) 利用前面得到的公式,给出下面的定理: 定理2:对于具有PD控制器的拥塞控制系统式(2),当R=R0时,Hopf分岔的方向和周期解的稳定性由式(25)和下述结果决定: (1)Hopf分岔方向由υ2决定。如果υ2>0,则Hopf分岔是超临界的,当R>R0时系统有周期解。如果υ2<0,则Hopf分岔是亚临界的,当R (2)Hopf分岔周期解的稳定性由β2决定。如果β2<0,则系统周期解的轨迹是稳定的;如果β2>0,则系统周期解的轨迹是不稳定的。 (3)系统Hopf分岔周期解的周期由T2决定。如果T2>0,则周期解是增加的;如果T2<0,则系统周期解减少。 选取与文献[14,21]中相同的参数,即N=50,K=0.001,C=1 000,Tp=0.3。当R=0.344时,R0=0.343 图1 R=0.344时无控系统的波形 为了推迟Hopf分岔的发生,加入PD控制器,设置比例和微分参数展示控制效果。当R=0.344,kp=-0.5,kd=-0.5,仿真图2表明系统出现周期解,是稳定的。 图2 R=0.344,kp=-0.5,kd=-0.5时PD控制系统的波形 为了弥补TCP协议在无线接入链路网络的局限性,引入应用于高速无线网络,完全符合高速无线网络特点的TCP Westwood协议的一种网络拥塞控制系统模型,即TCP Westwood/AQM网络的连续流体流模型,通过选择通信延迟作为分岔参数,分析无线网络系统中的Hopf分岔行为,当通信时延超过临界值时,系统会产生Hopf分岔现象。为了延迟Hopf的发生,引入PD控制器,利用中心流形定理和规范型理论,推导得出系统发生Hopf分岔的条件和反映Hopf分岔性质,方向和周期的参数数值,MATLAB仿真证明PD控制器能有效控制分岔,验证了理论分析的正确性。
2 Hopf分岔的方向和Hopf分岔周期解稳定性








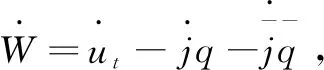


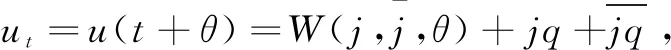

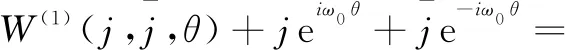



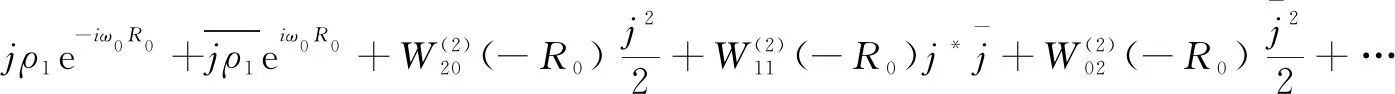

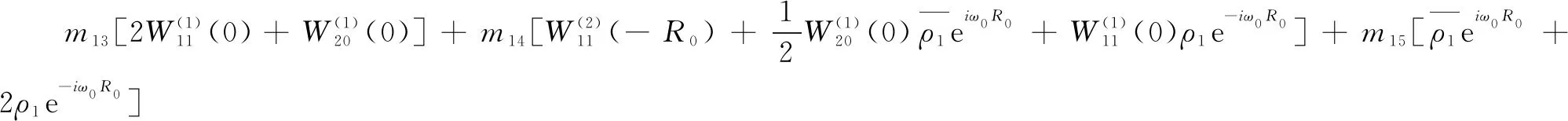

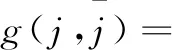

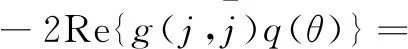
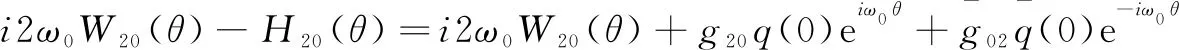



3 数值仿真


4 结束语
