基于无迹卡尔曼滤波的电池SOC估算与仿真∗

（青岛大学电气工程学院 青岛 266071）

1 引言

电动汽车行业的蓬勃发展，带动了车载锂电池的电池管理系统（Battery Management System，BMS）的研究深化，作为电池管理系统中的重要一环，电池剩余电量（State Of Charge，SOC）的精确级数制约着对电池能源的利用效率［1］，而如何提高估算精度，一直是电池领域科研事业的重中之重。目前国内通用的SOC估算方法［2］有基于电池自身特性的安时积分法，开路电压法，内阻法等；也有通过算法优化基础方法的卡尔曼滤波算法，BP神经网络算法［3］，粒子滤波算法等。其中鲍慧论文在原有安时积分法基础上进行四个系数的修正［4］，使SOC估算精度提高到5%以内，但其固有的系统累积误差没办法消除；林春景的基于电池内阻随温度变化进而求得电池状态［5］，对电池内阻特性进行了深入研究，不过内阻在电池满电时其变化特性和电池状态函数关系不明显，故该算法有一定局限性；商云龙所研究的神经网络和扩展卡尔曼滤波结合［6］，使电池估算精度极大地提高，可笔者认为该算法过于复杂，对器件要求精度过高，不适合应用在普通电池的BMS中。

本文基于二阶Thevenin模型下的无迹卡尔曼（Unscented Kalman Filter，UKF）算法，通过对得到的电池数据进行UT变换，得到相同概率密度下的SOC估算值，从而提高SOC估算精度。

2 锂电池模型

2.1 锂电池模型原理

本文在传统的Thevenin模型的基础上搭建二阶Thevenin模型，如图1。相较于一阶模型，二阶模型综合考虑了电池的电化学极化和浓差极化现象，能更精确地反映化学反应程度，实时模拟电池状态，进而提高SOC的估算精度［7］。

图1 二阶Thevenin模型

该模型的数学表达式为

通过对电池研究发现，电池模型中各个路原件随着电池剩余电荷量的变化不断波动，为更好反映电池本身情况，分别对电池模型中电路原件和SOC进行拟合确定函数关系。对电池进行HPPC脉冲放电实验，分别截取不同电池初值放电后的静置曲线［8］。在CFtool工具中，结合基尔霍夫定律和二阶电路全响应分析得到该模型的拟合方程。

图2 HPPC脉冲放电实验电流电压变化曲线

以图2为例对180s～300s电压曲线以式（3）进行拟合得到该SOC下的各个参数，分别拟合不同SOC初值下的极化现象曲线并进行参数辨识。其中已知电池的脉冲电流，电池的开路电压a为稳定后的电压值，电池浓差极化现象的时间常数c取值固定，而由于电化学极化现象不明显，其时间常数的取值总是波动，为提高拟合曲线的精度，对各SOC值下时间常数e的取值进行数据处理将其固定。则各SOC初值情况系的电路元件系数可求。截取部分实验数据如表1。

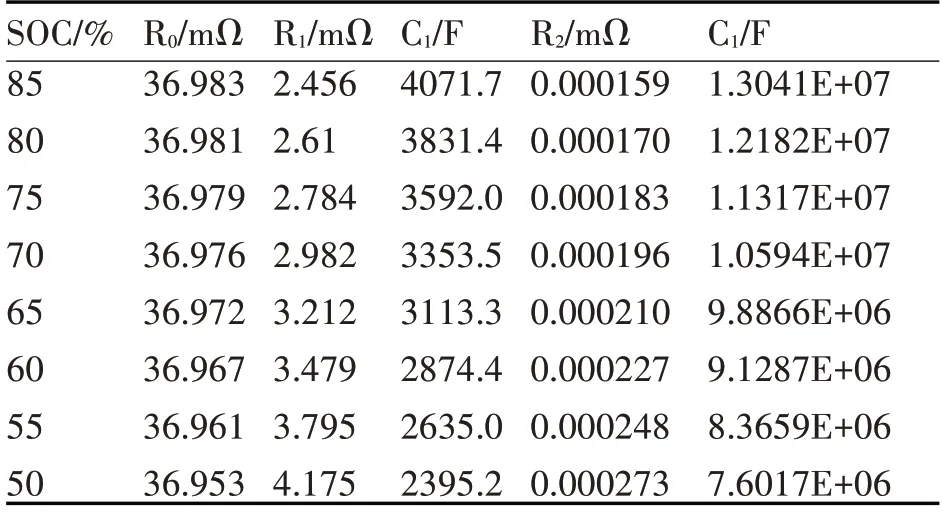
表1 截取部分实验数据

在Cftool工具中分别将R0、R1、C1、R2、C2…与SOC拟合，并将拟合函数用于搭建仿真模型。同时根据记录下来的电压值可得到电池的SOC-OCV曲线，如图3。对其关系进行五阶函数拟合得到关系式：

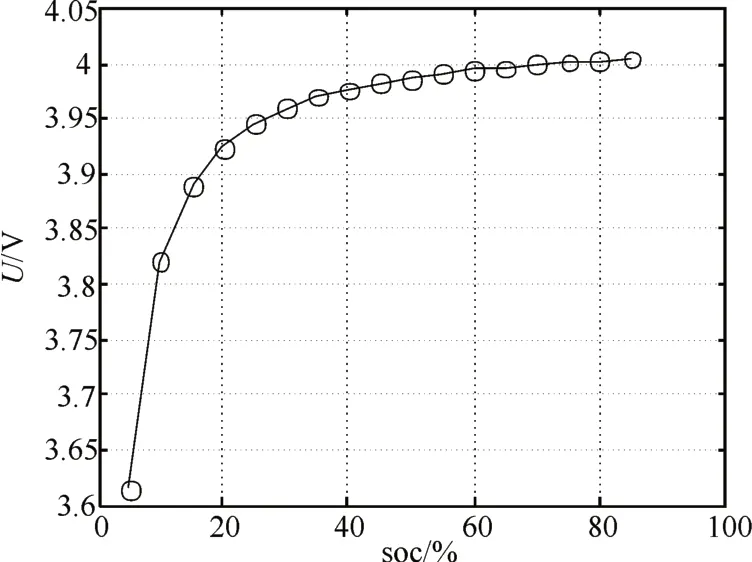
图3 SOC-OCV曲线

2.2 二阶仿真模型

根据已有电池原件及其函数关系在Matlab/Simulink搭建电池模型，如图4。

采用国标QCT 897-2011中的工况电流三来测试该模型的稳定性，其真实电压和模拟电压对比如图5，其误差控制在1.5%以内，分析电池模型可知该误差主要由工况电流反向充电引起，因本仿真只考虑电池放电故其存在的仿真误差在接下来放电实验可避免。

图4 二阶仿真模型

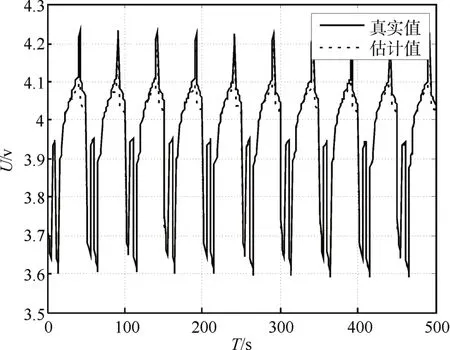
图5 工况电流三实验电压对比

3 卡尔曼那滤波

3.1 卡尔曼滤波原理

卡尔曼滤波器实际上可以看做是状态变量在由观测矩阵生成的线性空间上的映射，进而通过观测矩阵来修正估计的状态方程。由于电池状态的变化是非线性的，所以应生出扩展卡尔曼滤波算法，将非线性的电池系统离散化，使之适用于线性的卡尔曼滤波器［9～11］。其中卡尔曼滤波的状态方程和测量方程分别为

状态方程：

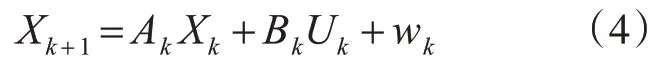
观测方程：

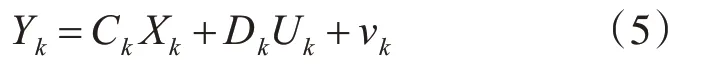
式中Xk为状态矩阵，Uk为控制矩阵，Yk为观测矩阵，Ak状态转移矩阵，Bk为状态控制矩阵，Ck为观测矩阵，Dk为观测控制矩阵，wk为k时刻的动态噪声，vk为k时刻的观测噪声。将卡尔曼滤波算法，安时积分法和二阶Thevenin模型结合得到式（6）和式（7）。

将卡尔曼滤波算法和电池模型相结合的程序框图如图6所示，将电池的输出电流和端电压作为输入，电池的SOC作为输出，用已经求得的开路电压曲线来修正安时积分法所输出的SOC值。

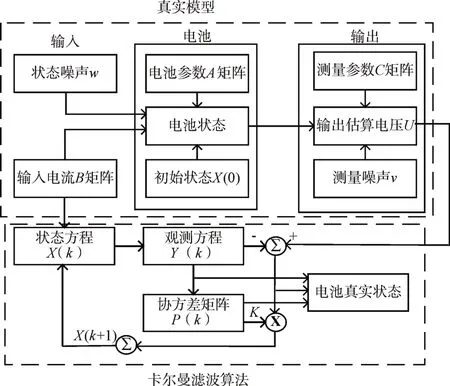
图6 卡尔曼滤波算法

3.2 无迹卡尔曼滤波原理

无迹卡尔曼滤波也是基于卡尔曼滤波原理的一种应用［12］，不同于扩展卡尔曼滤波对电池模型进行泰勒级数展开并略去高阶无穷小项，虽然使电池模型线性化，但在其过程中被忽略的高阶所带来的误差，会引起滤波器精确度降低以至于发散［13］。

UKF算法对电池模型中函数关系的概率密度进行分析［14］，通过无迹变换得到估计值对应的sig⁃ma点，由一系列的sigma点来逼近状态的后验概率密度，从而保证估计值的准确性，避免了对状态转移矩阵和观测矩阵求其雅各比矩阵的复杂运算，同时也没有忽略高阶项对矩阵的影响，从而保证估计值的准确性，式（8～9）为UT变化方程，即通过UT转化确定sigma点及其权重。

其中下标c表示协方差的权重，下标m表示均方差的权重，λ=α2(n+κ)-n，λ代表缩放比，α=0.01表示采样点的分布状态，当α较大时表明平均值处sigma点权重越大，β=2是权数，用来合并方程中高阶项的动差，κ=3-n。

首先列写基本的状态方程和从测量方程。

代入式（8～9）进行UT变换，得到k时刻的X列向量的sigma点矩阵。

将矩阵式（11）代入式（10）中的状态方程，求得下一时刻的系统状态。

此时得到的是X(k+1|k)时刻的状态矩阵，由式（9）求X(k+1|k)的加权均值和更新后的协方差矩阵。

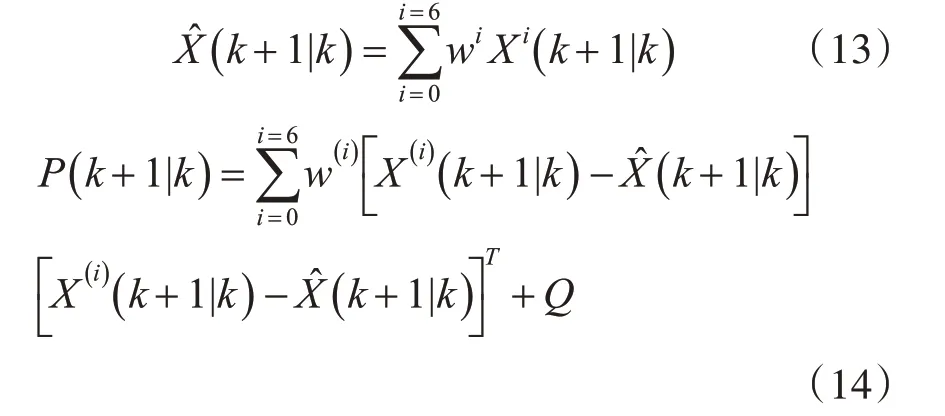
根据更新后的状态矩阵式（13）和协方差矩阵式（14），再次使用UT变换，产生新的sigma点集，并将该点集代入式（10）中的观测方程得到估计的观测值，通过两次的UT变换使估测的观测值具有系统代表性。

同样的由式（10）加权求得到估计预测值及其协方差。

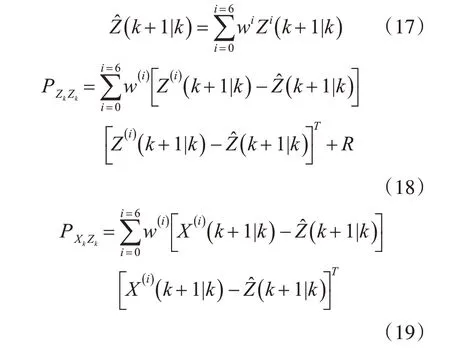
根据式（18～19）可求得Kalman增益系数K，并通过增益系数K更新系统的状态和协方差矩阵。

4 实验验证与仿真

在Matlab/Simulink中搭建电池放电电路［15］，通过Pulse Generator模块产生周期为200s占空比为80%的电流脉冲信号，同时为模拟工况，分别在电流采集和电压采集处添加高斯白噪声，将带有噪声的信号作为输入，经S-Function中的UKF滤波后，输出到示波器中，仿真如图7。

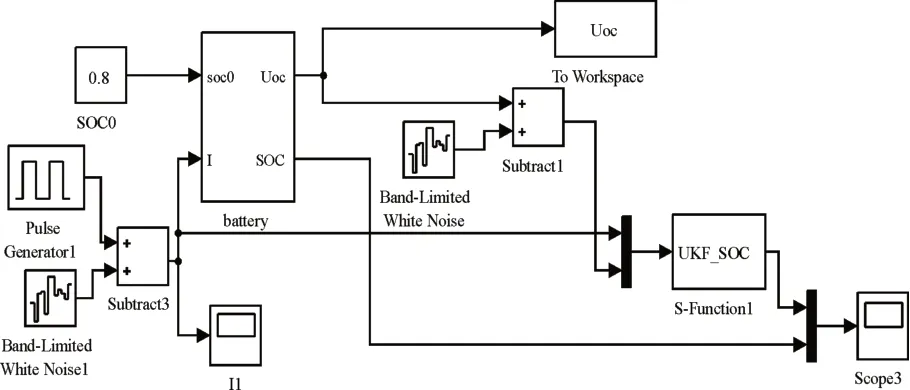
图7 仿真图

将输出结果用Matlab画图表示，图8是在SOC初值为85%时的电池模型输出结果，图9是EKF算法UKF算法分别和真实值做残差；由图像分析得相较于EKF算法3%的误差，UKF算法可将误差控制在1.5%以内。

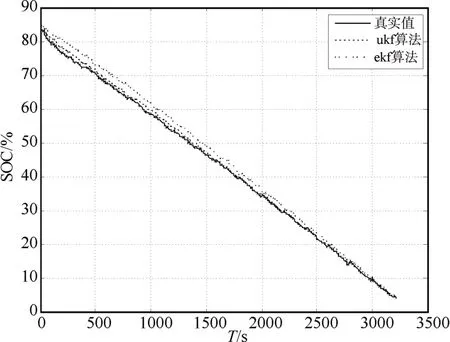
图8 初值为85%时SOC估算曲线

图9 初值为85%时误差对比曲线

图10和图11是在SOC初值错误的情况，观察其对应算法的修正能力，由图11残差对比图可以较为明显地观察到UKF算法会超前于EKF算法追踪到真实的电池状态，验证了UKF算法具有更优秀的收敛性和鲁棒性。

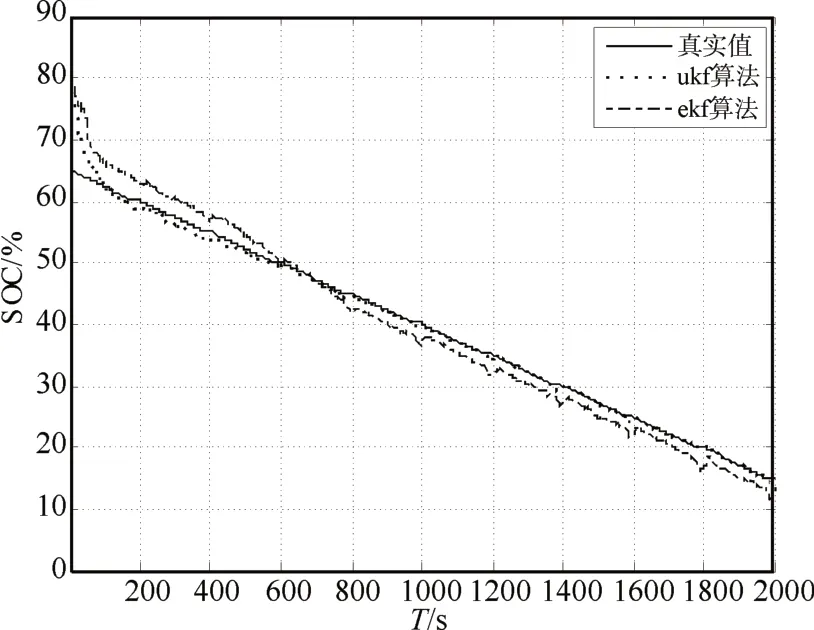
图10 初值有误差时SOC估算曲线

图11 初值有误差时误差对比曲线

5 结语

本文从常规的扩展卡尔曼滤波算法框架中加入无迹变换，提出了一种基于无迹卡尔曼滤波算法的电池SOC估算方法，建立二阶Thevenin电池模型，并在Matlab/Simulink对EKF和UKF算法进行了仿真对比。结果表明UKF算法相较于EKF算法具有更优秀的收敛性和鲁棒性，具有实际价值。本算法的局限性在于没有对电池充电情况进行考虑，如电池模型仿真时，在工况电流条件下电池存在反向充电电流，其电池模型相对于放电模型有细微差别，故该实验仍有很大的优化空间。