绝缘子在偏心冲洗时有效冲洗面积的研究∗
2021-04-04
(西南交通大学先进驱动节能技术教育部工程研究中心 成都 610031)
1 引言
带电水冲洗指的是在保证电路正常通电的状态下利用高压水射流对其外部绝缘设备表面的污秽颗粒进行清洗[1]。带电水冲洗高效率、低成本等优势在一定程度上满足了经济发展的需要[2~3]。污秽颗粒脱离绝缘子表面的方式主要有滑动脱落和滚动脱落两种方式,根据国外学者Mehdi Soltani&Goodarz Ahmadi的研究,在颗粒脱离过程中滚动脱附方式占主导且滚动脱附所需的临界水流速度小于滑动脱附[4],因此大于滑动脱附所需的临界水流速度的速度区域即为有效清洗面积,而有效冲洗面积的大小直接影响到水冲洗的效率。
2 污秽颗粒的脱附机理
根据JKR颗粒脱附模型可知,使得一个球体颗粒从其吸附的平面脱落所需要的最小力[5]为

其中,d为球体颗粒的直径大小;WA为附着力的热力学工。
污秽颗粒的脱附主要有滑动脱附和滚动脱附两种方式,其受力分析如图1所示[4]。

图1 球形颗粒黏附在光滑表面的几何特征
2.1 滚动脱附
如图1所示,一个颗粒受到一个外力Ft在O点所产生的力矩大于由颗粒的黏附力所产生的力矩,使得颗粒通过滚动脱附的方式脱离光滑平面,即

式中,Ft为作用在颗粒上的切向外力;α0为颗粒中心到平面的距离;Mt为是表面压力相对颗粒球心的转矩;FL为提升力;Fp为颗粒的黏附力。
当采用流体冲洗表面所粘附的颗粒时,静止颗粒受到的流体剪切力由O'Neill计算得[6]:

式中,u为粒心处的流体速度;d为颗粒直径;μ为流体粘度;f为为壁面效应的校正因子;CN为拉力校正因子;C为Cunningham校正因子。
把JKR模型中的式(1)代入颗粒的子层模型中并联立式(2)和式(3)可得到颗粒从平面滚动脱附所需的临界剪切速度ur[4],

式中,ρ为流体的密度。
2.2 滑动脱附
当粒子所受到的外力大于其最大静摩擦力时,颗粒通过滑动脱附的方式脱离平面,即

式中,Ft为作用于颗粒且与平面平行的外力;k为静摩擦因子。
运用JRK模型,颗粒发生滑动脱附的临界剪切速度[4]为

3 临界剪切速率的计算
绝缘子污秽的粒度分析显示,污秽粒径大致呈正态分布,九成以上污秽颗粒的粒径均小于50μm[7],崔燕通过自由沉降实验发现,沉积颗粒的平均粒径为20μm[8]。而附着在绝缘子上的污秽中主要的不溶物成分都是CaSO4和SiO2[9~10],因此该研究主要以成份为CaSO4和SiO2且粒径d为20μm的颗粒为研究对象进行计算分析。查阅相关资料[11~12]可得

将以上值代入式(4)和式(6)中,分别求得两种脱附方式流体在粒心处的临界剪切速度为ur=0.0386m/s,us=0.5171m/s。流体在壁面的速度为0,根据剪切速率的定义可以求得两种情况下的临界剪切速率为3860s-1和51710s-1。
4 模型的建立与网格的划分
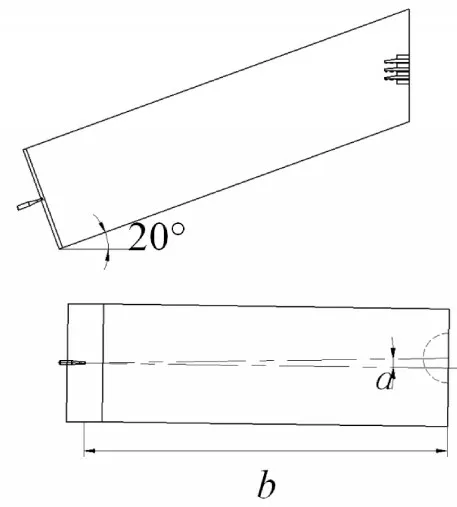
图2 三维流体域的模型图
利用solidworks建立如图2所示的喷嘴仰角为20°[13],靶距b为3000mm的三维流体域实体,喷嘴的水平偏转角为α。采用如图3所示的锥形喷管,该锥形喷嘴的主要结构参数为喷嘴的入口直径D,喷嘴的内锥角β,喷嘴出口直径d=5mm,喷嘴圆柱段长度为l,喷嘴接入段的长度n。其他参数分别为喷嘴的内锥角β为13°[14],l/d=3,n/D=4,D=2d[15]。在建模时使得喷嘴的出水面与其轴心垂直,有效地避免了水柱的过度发散。
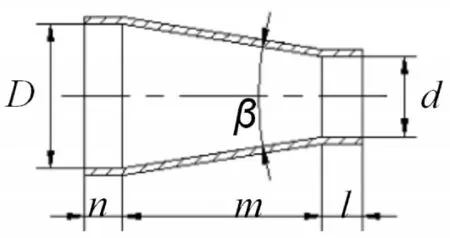
图3 喷嘴模型
为了提高仿真结果的可靠性以及计算效率,同时也要保证网格对复杂模型的自适应性,该研究采用如图4所示的混合网格。提高了网格对复杂曲面的适应性,同时也在一定程度上保证了网格的质量。

图4 流体域网格
5 边界条件的设置
将水的入口边界设置为压力入口,出口边界设置为压力出口,并设置好与入口压力相关的湍流强度以及水力直径。在fluent中选择vof模型中的Re⁃alizable k-ε方程模型,压力速度解耦采用piso算法,动量采用quick算法,能量及湍流参数的求解采用二阶迎风格式,在保证计算精度的前提下,尽可能地提高了计算速度。
6 仿真结果及分析
根据GB/T 13395-2008《电力设备带电水冲洗导则》中不同水冲洗方式下的喷口直径大小,针对绝缘子带电水冲洗小水冲、中水冲、大水冲三种情形选择出口直径d为3mm、5mm、8mm的喷嘴。
由于绝缘子的壁面大多是由很多曲面组成的一个复杂的旋转曲面,不能直接从仿真结果中直接读出绝缘子近壁面的剪切速率的大小,因此将仿真结果导入cfd-post中做如下处理:
1)在绝缘子壁面创建一个如图5所示的壁面剪切云图,并将云图分为两个颜色等级,仅显示大于51.71pa的区域,如图5所示;
2)利用剪切应力大于51.71pa的区域创建一个如图7所示的面域,并计算该面的面积大小即为有效冲洗面积的大小。

图5 绝缘子壁面剪切应力云图

图6 大于51.71MPa的剪切应力云图

图7 剪切应力大于51.71MPa的面域
由前文可得,滚动脱附的临界剪切速率为3860s-1,滑动脱附的临界剪切速率为51710s-1,为确保冲洗效果,因此选用更难达到的滑动脱附方式的临界剪切速率作为有效冲洗面积的判断依据。而根据剪切速率与剪切应力的关系:
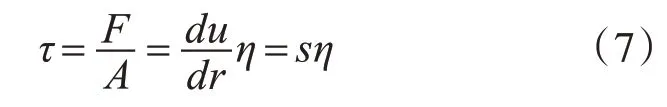
式中,τ为剪切应力,Pa;s为剪切速率,s-1;η为动力粘度,Pa·s。
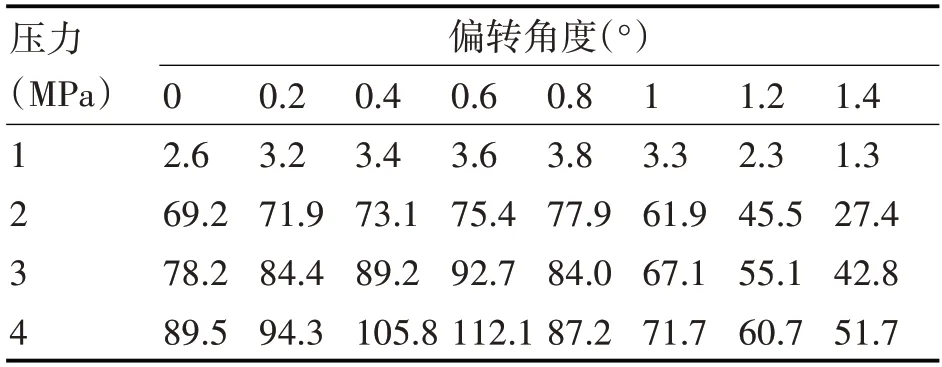
表1 喷口为3mm水射流的有效冲洗面积(cm2)
水在20°C时的动力粘度为1.01×10-3Pa·s,代入式(11)可得,滑动脱附所需的临界剪切应力为51.71Pa,因而在cfd-post中绝缘子壁面剪切应力大于51.71Pa的区域就是有效冲洗区域。
通过利用cfd-post完成后处理,小水、中水、大水冲洗方式下的有效冲洗面积仿真结果如图8~10所示。
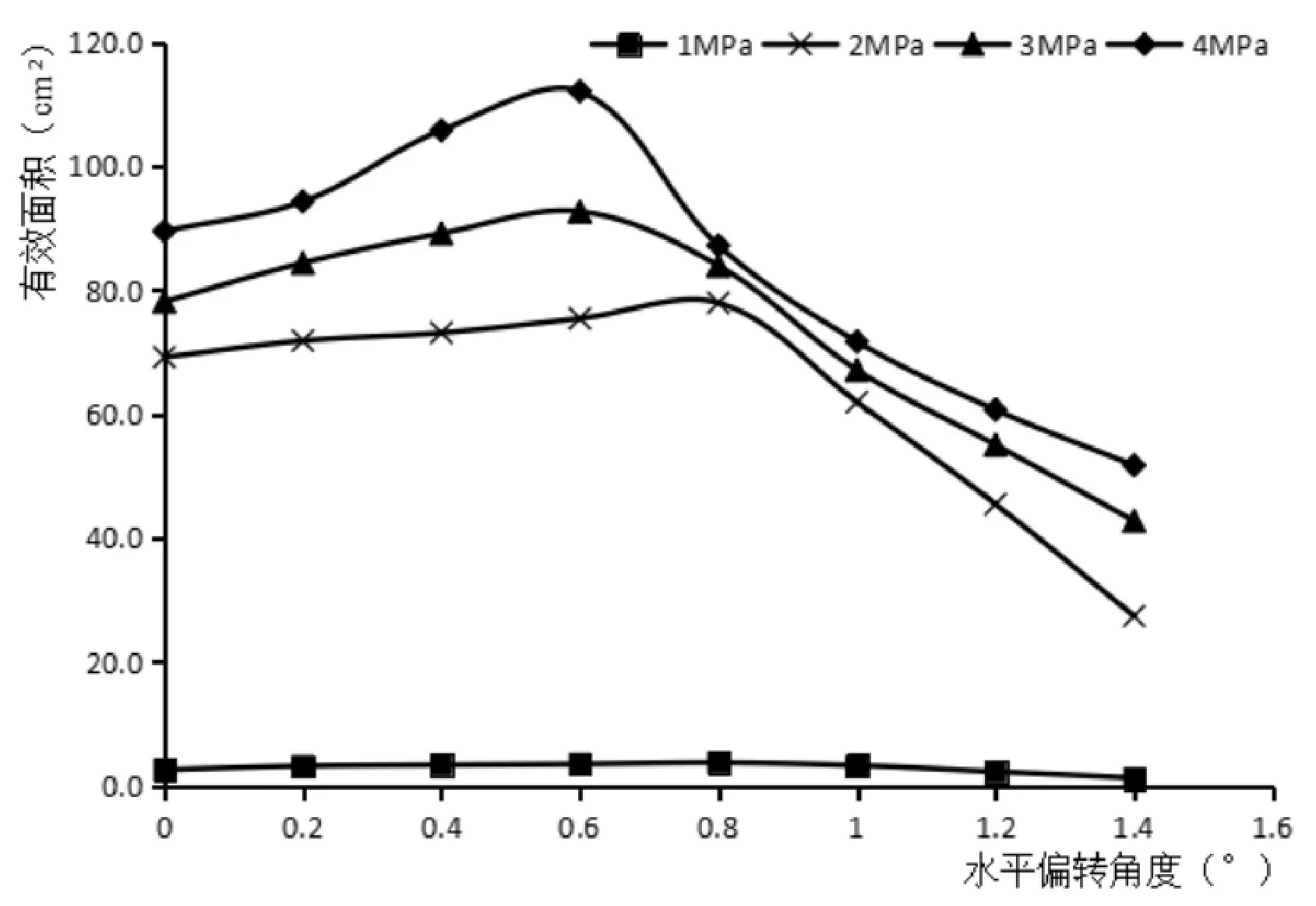
图8 3mm有效清洗面积的变化
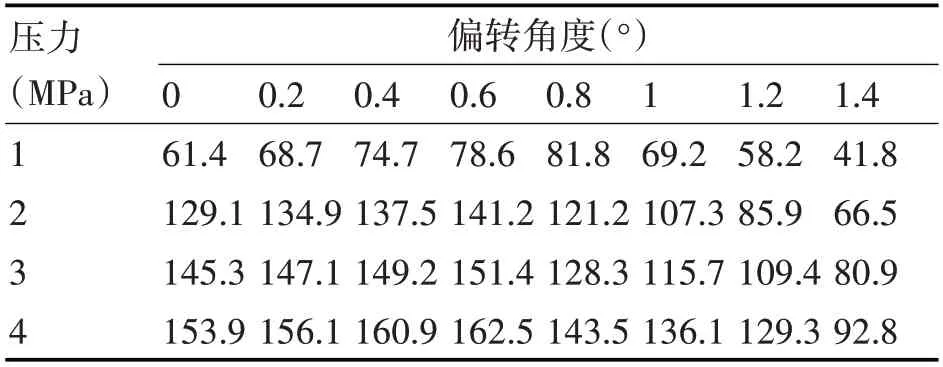
表2 喷口为5mm的有效冲洗面积(cm2)
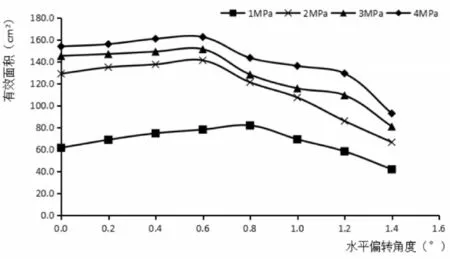
图9 5mm喷嘴有效冲洗面积的变化
从图8、9可以看出,利用小水和中水的冲洗方式对绝缘子壁面进行冲洗时,随着喷嘴水平偏转角度的增大,有效冲洗面积先增大然后减小;且随着压力的增大,有效冲洗面积的随偏转角度变化的转折点更靠近小的水平偏转角度。

表3 喷嘴为8mm的有效冲洗面积(cm2)
显然,图10所示的出口直径为8mm喷嘴的有效面积的变化趋势与3mm和5mm的喷嘴在较小的水平偏转角度下的变化完全不同,在较小的水平偏转角度时,8mm喷嘴的有效冲洗面积基本上维持不变,进一步增大水平偏转角,有效冲洗面积才随之减少。这是由于喷嘴直径为8mm的大水冲洗方式在对该绝缘子的清洗作业上已经达到了“饱和”状态,在该工况下,增大入口压力的大小并不能使有效冲洗面积有明显的提高。
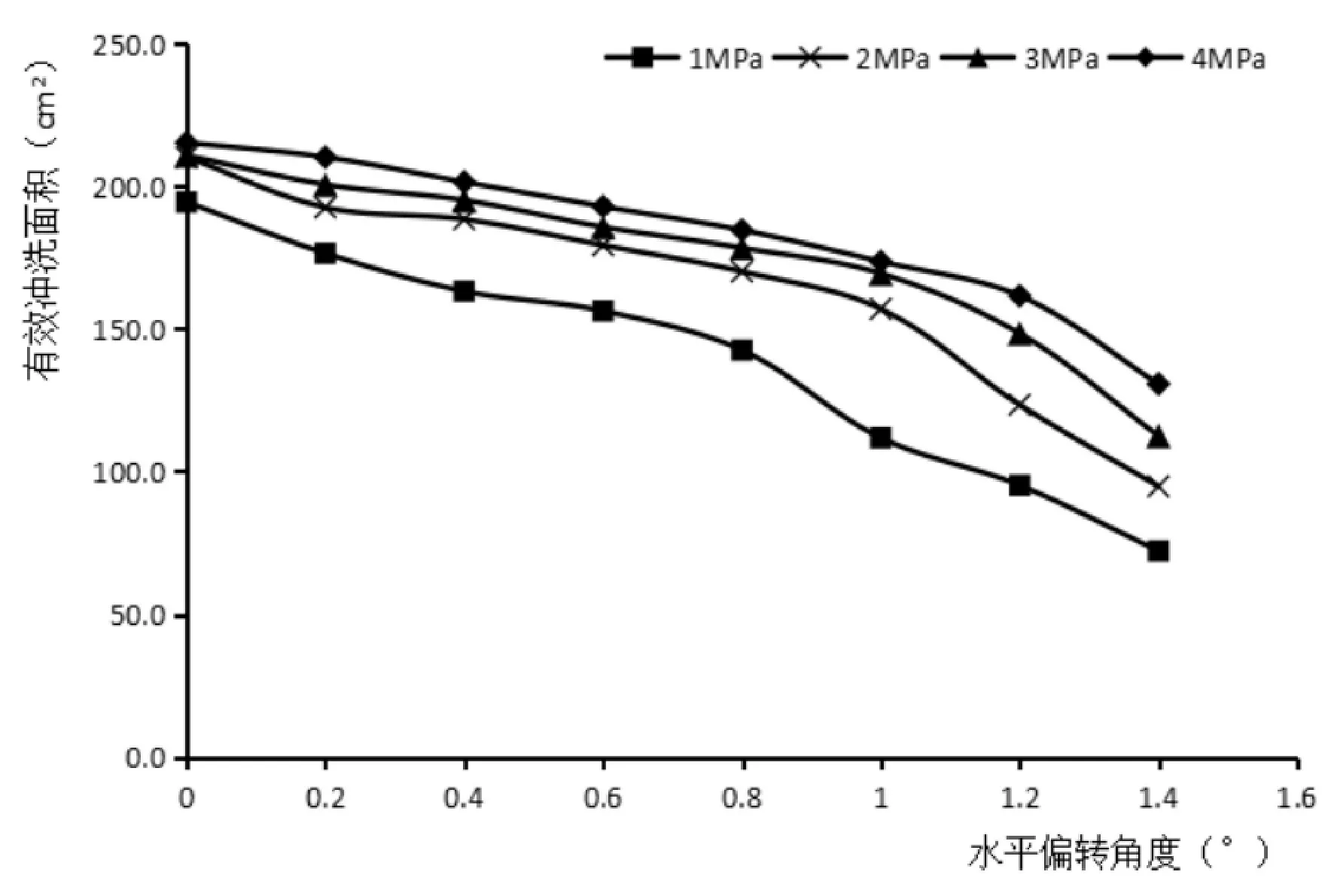
图10 8mm喷嘴的有效冲洗面积
7 结语
本文利用fluent对小水、中水、大水三种方式的绝缘子偏心水冲洗下的有效冲洗面积进行了仿真计算,对仿真结果进行了对比分析,得到了以下结论:
1)小水和中水冲洗方式下,有效冲洗面积随着入口压力的增大而增大,但其增长幅度会随着压力的增大而减小;
2)当入口压力一定时,随着水平偏转角度的增大,绝缘子伞裙下表面上的有效冲洗面积增大,而由水射流回转水和溅射水冲洗的卷源自伞裙上表面和内盘柱上的有效冲洗面积减少的幅度增大,从而导致了有效冲洗的总面积先增大后减小;
3)用大水冲洗的方式对该型号的绝缘子进行水冲洗时,会使得在绝缘子伞裙下表面的有效冲洗面积达到饱和,导致了随着水平偏转角度的增大,有效冲洗面积呈持续下降状态。
