布氏硬度自动测量中多圆检测方法∗

（东北大学软件学院 沈阳 110819）

1 引言

硬度是材料最重要的参数之一，其测试在生产过程中具有非常重要的意义。布氏硬度以其测量精确度高、可重复性好等优点，得到了广泛应用。布氏硬度试验方法原理为以一定的压头和试验力在试样上压出压痕后，测量试样表面压痕的直径，换算为布氏硬度［1］。

传统的布氏硬度测试方法采用读数显微镜人工测量压痕尺寸，基于机器视觉的测量具有非接触式、测量速度快、精度高、柔性好等特点，越来越受到重视，其关键是检测并准确测量压痕圆的直径。另外圆检测在很多方面都有应用。如虹膜检测［2］，细胞计数［3］、圆形器件或图标识别和定位［4］，圆形物计数［5］，标记定位［6～7］等。

目前圆检测方法主要有三类：圆霍夫变换、随机抽样一致性（random sampling consistency，RANSAC）和最小二乘法，以及它们的改进［8～12］。这些方法在特定领域内均取得了良好的效果。但它们均假定边缘检测到的绝大多数点为圆周上的点，而且难以处理圆分裂或者多圆的情况，影响了其实用价值。本文根据分裂圆的特点，利用部分圆周与其最紧致矩形的切点关系、找到三个确定的切点求初始圆，自动判别属于同一圆的不同部分，且能检测多个圆。利用凸包滤除非圆周点，结合迭代纯化最小二乘法，可以得到精确的圆半径，实验表明了本方法的有效性。

2 布氏硬度圆的特点与分析

2.1 布氏硬度圆的特点

在实际应用中，尤其是布氏硬度测量，检测圆时经常遇到多个圆、圆分裂、圆残缺不全的情况，如图1所示。一般的做法是，对图像进行预处理、阈值化、边缘检测之后，采用圆Hough变换或最小二乘得到圆心和圆半径。大多数圆检测方法适用于单个圆检测，如果是多个圆的情况，则需要明确给出圆的个数或百分比。

对于图1中的几种情况，传统方法存在以下问题：1）对于多个圆，一般需要给出准确的圆个数或百分比，难以完全自动化；2）如果圆分裂，难以确定哪些分裂部分属于同一圆，从而影响到圆检测的准确性；3）对于不完整圆，由于检测结果不可靠，一般采取放弃的策略；4）即使对于完整的圆进行检测，也严重依赖于边缘检测的精度，而由于实际采集的图像中噪声的影响，边缘点位置的偏差对造成最终检测到的圆心位置或半径的偏差。

图1 布氏硬度压痕圆图像

本文提出的方法能很好地解决上述问题。本文方法的优势在于：1）能够自动判断圆是否分裂，对于分裂的圆，能够自动将分裂的各部分合并为一个完整的圆；2）能够自动检测多个圆，而毋需给出圆的个数或百分比；3）采用迭代纯化最小二乘法，能够得到亚像素的圆心和半径，对部分圆也能够准确检测。

2.2 部分圆及其最小外接矩形的切点

图像中的局部区域，可以用矩形框包围。这些矩形框可以有多个，其中面积最小的称为最小外接矩形。

完整圆弧的最小外接矩形为正方形，圆弧与外接矩形的切点是正方形各边的中点。据此可以判断圆是否分裂，同时估算圆心位置和半径。

对于部分圆弧，有如下的定理：

定理1部分圆弧的最小外接矩形边长不全相等，最小外接矩形长边的中点在圆弧上，且是其与圆弧的切点。

证明：如图2所示，实线表示以圆弧的弦为一条长边的外接矩形，显然其另一条长边在中点与圆弧相切，设该矩形的长和宽分别为L与W，而其他任意的外接矩形（用虚线表示）的长和宽分别为L'与W'，两个外接矩形的夹角为θ，则有：

以上两式左右两边分别相乘，可得：

因此圆弧的最小外接矩形长边的中点是圆弧与矩形的切点，短边与圆弧相交或相切。

根据此定理，在得到一段曲线的最小外接矩形后，就可以根据矩形长边中点是否为曲线点来确定该段曲线是否为圆弧，如果是圆弧，则可以得到圆弧上三个点，从而得到相对确定的候选圆。

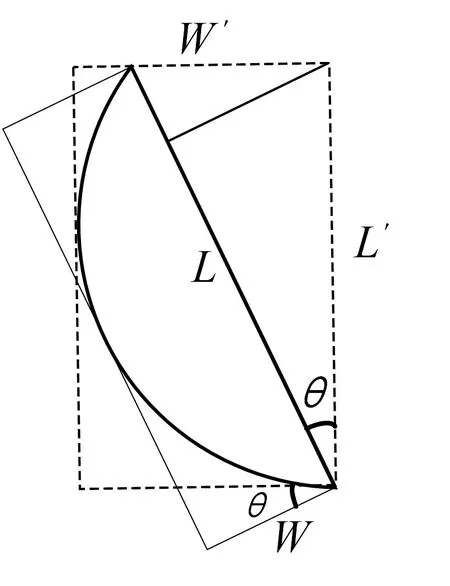
图2 部分圆及其最小外接矩形

2.3 圆交叉的判断及合并

如果一个圆分裂成两个或多个部分，则各个部分的外接圆之间有交叉，即两圆半径之和大于圆心之间的距离。对于交叉的圆，需要进行合并。设圆Cp、Cq的圆心分别为(xp,yp)、(xq,yq)，半径分别为Rp、Rq，则合并后的圆心和半径分别为

图3 轮廓（实线）及凸包（点）

2.4 区域凸包

区域凸包是指区域的外接凸多边形，这个凸多边形将该区域所有像素点都包含在内［13］。将合并之后的圆的各部分看作一个区域，则原来部分圆的圆弧部分将会包含在凸包点中，而非圆弧部分由于违反凸包的外凸特性，所以不包含在凸包点中。如图3所示。图中实线为圆区域轮廓，虚线为其凸包。可以看出，凸包可以将分裂圆上的非圆弧点排除，同时如果分裂圆内有区域，其轮廓点也不会保留。但凸包轮廓点中也包含非轮廓点，可以通过凸包与原区域轮廓点求交集得到合并圆弧点。

3 迭代纯化最小二乘拟合

如果能够得到三个以上同属一个圆的圆弧点，就可以利用圆Hough变换法或最小二乘拟合，得到较为精确的圆参数［12］。圆Hough变换要遍历三维参数空间，对内存和时间的消耗特别大，且检测结果精度受参数离散化程度的影响也大，但近年来提出了很多改进算法。最小二乘法理论严密、精度高，拟合效果佳，是目前圆测量的主要方法［12］。

在实际图像的获取和处理过程中，难免会受到各种干扰，造成检测到轮廓点不准确，或者将噪声点误认为轮廓点，影响最终拟合结果。而最小二乘法在圆拟合时尽量去适应所有点，包括噪声点和不准确的轮廓点（本文称之为离群点），显然这些离群点会大大影响拟合精度。为此提出RANSAC圆拟合算法［11］，但RANSAC算法中抽样耗时占算法总耗时的比重较大，且RANSAC并不能保证结果一定正确，为了保证算法有足够高的合理概率，必须小心的选择算法的参数（参数配置）。但在圆拟合过程中，特别是在离散点非均匀采集的情况下，经常会出现只运用最小二乘法时拟合精度不高的状况。

为了克服以上方法的局限性，本文提出迭代纯化最小二乘法。与文献［12］的方法不同，本文方法主要是基于3σ准则［14］。在前次最小二乘拟合的基础上，剔除离群点之后再进行最小二乘拟合，直到符合设定条件为止。而文献［12］提出的迭代优化最小二乘圆曲线拟合方法，是为了提高离散点非均匀采集情况下的拟合精度，并不剔除离群点。

根据3σ准则，干扰或噪声造成的奇异数据的难以满足正态分布。设μ代表均值，σ代表标准差。根据数理统计，观测值分布在（μ-3σ，μ+3σ）中的概率为0.9973。因此可以认为，观测值几乎全部集中在（μ-3σ，μ+3σ）区间内，超出这个范围的可能性仅占不到0.3%。如果一组测量数据中某个测量值的残余误差的绝对值大于3σ，则可认为该测量值为异常值，应剔除，不参加拟合。

本文提出的迭代纯化最小二乘圆拟合算法如下。

输入：N个轮廓点的坐标{(Xi,Yi)|1 ≤i≤N}，允许标准差σ，迭代次数j=0。

输出：圆心坐标(xC,yC)和圆半径R。

步骤2：根据每一个轮廓点坐标和上一步得到的圆心坐标，计算轮廓点和圆心之间的距离（轮廓点半径），计算其均值（平均半径）Rj和标准差；

步骤3：对每一个轮廓点，计算轮廓点半径与平均半径差的绝对值

步骤4：若轮廓点数Nj＞10且σj＞σ，剔除掉的轮廓点，得到新的轮廓点集，重复步骤1～步骤3。

否则，结束。

4 算法流程

本文方法的流程框图见图4。输入为待检测图像，输出为一个或多个圆心坐标和半径值。算法说明如下。

1）由于布氏硬度检测的压痕圆表面平滑，非圆部分一般较为粗糙，其成像结果表现为压痕圆部分灰度较低且灰度变化小。因此先进行图像增强，强化图像灰度变化。一般可采用像素局部方差、梯度强度和信息熵，这三种值越大，则灰度变化越大，反之亦然。根据布氏压痕圆图像的形成机理，也可采用Gabor滤波［15］进行增强。

2）对增强后的图像采用Otsu法进行二值化［16］。由于噪声干扰，且工件表面不平整，取阈值之后有许多细小的非圆坑黑点，采用数学形态学运算去除孤立小目标，形成多个连通区域。进而提取每个目标区域的轮廓。

3）根据目标区域轮廓，得到其最小外接矩形。根据目标区域最小外接矩形的面积和长宽比，可以排除非圆区域。

图4 本文方法流程框图

4）根据2.2节的方法，判断最小外接矩形长边中点是否在圆弧上，如果在，则该轮廓为候选圆弧。由长边中点、两条短边上与短边中点最近的圆弧的公共点，得到三点，根据这三点得到初步圆。判断相邻的两个区域的初步圆是否有交叉，如果有交叉，则按照式（3）进行合并。并将它们的轮廓点归并。

5）圆归并后，其轮廓点中包含非圆弧点，不能直接拟合。为此，对归并的区域，求合并圆的凸包。求合并区域的轮廓点与凸包点的交集，得到的点大概率为最终所求圆轮廓点上的点。

6）按照第3节的方法，进行迭代纯化最小二乘拟合，得到最终所求圆。输出圆心坐标与半径值。

5 实验结果与分析

本文的研究目标是准确检测出在实际生产环境下布氏硬度测量图像中可能分裂的多个圆，并精确测量其半径。为了验证本文方法的有效性，在Windows10平台上，采用Python 3.5语言，结合OpenCV3.0，实现了本文圆检测及拟合算法。计算机配置为Intel Core i5-2400处理器，主频3.10G Hz，内存4G。实验图像为用布氏硬度计实际拍摄的图像，部分典型图像如图1所示，图像分辨率为1024×1280。由图中可看出，布氏硬度图像存在光照无法统一、背景纹理复杂多样、尺度大小不一、圆个数不定、圆面光照不均等特点，给圆检测及测量造成困难。

5.1 本文方法结果

图1（a）中的圆明显分为两部分，图5给出了本文方法的主要中间结果及最终结果。由图5（a）可以看出，纹理增强极大突出了圆坑与周围背景的对比度，给后面取阈值带来很大方便。虽然经过二值化、形态学滤波之后，仍然有少数噪音点，但通过面积、长宽比等排除掉几乎所有的噪音点，我们只需要在保留下来的目标区域求最小外接矩形，并判断长边中点是否为圆弧切点，如图5（c）所示。图5（d）中的细线圆为各目标区域的初步圆，同一圆分裂后的各部分之间有交叉，可以被合并。粗线圆为合并后的圆。图5（e）为圆弧轮廓点与区域凸包点求交集后的结果，可以看出，只有区域的最外围的轮廓点被保留下来，但此时轮廓中仍然可能包含小突起噪声点。对此我们采用迭代纯化最小二乘拟合，逐步排除这些离群点的影响，就可以得到精确的圆半径。

检测到圆并得到亚像素的圆半径值之后，结合摄像机标定值，可以得到实际圆坑半径大小，进而得到布氏硬度值。

执行效率方面，平均每幅图像处理时间为29.4ms，满足硬度计的实际要求。

5.2 与其他方法的比较

为了检验本文方法的性能，在实拍的28幅布氏硬度压痕图像（每幅图像可能有一个或多个圆，共47个圆）上，将本文方法与目前常用的典型方法做了对比。这三种方法分别是曲率辅助的霍夫变换（CACD）［5］，经典霍夫变换（CHT），和随机霍夫变换（RHT）［11］，四种方法的检测结果见表1，其中准确率=正确检测数/（实际数+误捡数）。图6是四种方法对图1（f）的检测结果。

图5 图1（a）圆检测的主要中间结果及最终结果

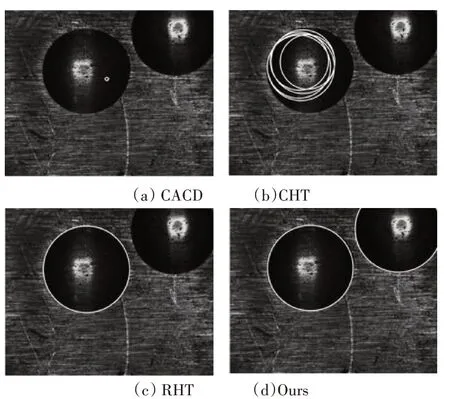
图6 各方法对图1（f）圆检测的效果

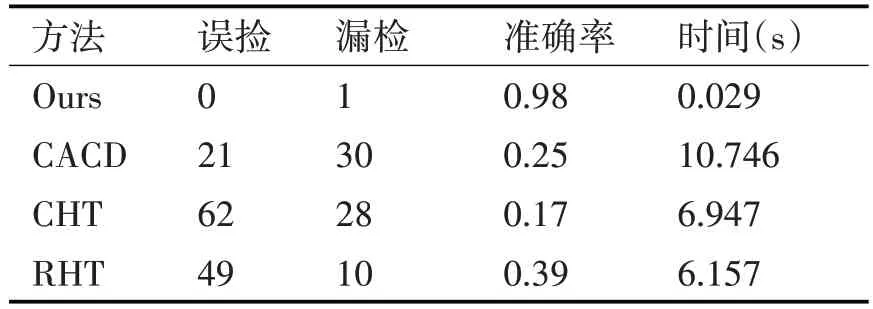
表1 四种方法的平均准确率及运行时间

用于比较的三种方法均是在阈值化之后的基础上检测圆的，可以看出三种方法均不能检测到所有圆，具有随机性。CACD方法由于要进行弧长归一化，倾向于检测小圆，CHT方法检测多圆个数不能确定，RHT方法倾向于检测完整圆。本文方法可以处理多圆、分裂圆、部分圆的情况。

对28幅实拍图像统计，四种方法的平均准确率和平均每幅运行时间对比如表1所示，可以看出本文方法运行效率最高。

6 结语

圆检测在很多方面都有应用，尤其在布氏硬度测量中，压痕圆的提取与测量是其关键。本文方法在纹理增强二值化的基础上，采用最小外接矩形切点判断，准确得到圆弧上的三个点，得到了基本确定的候选圆。圆交叉和合并能够处理圆分裂的情况，求凸包有效保留最外圆弧点，迭代纯化最小二乘拟合更进一步剔除了非圆弧点，并且得到亚像素半径值，为布氏硬度的精确测量打下了基础。今后将研究本文圆检测方法在其他领域的应用，以及维氏硬度压痕图的提取等。