基于节点加权和边加权的重分形研究∗
2021-04-04
(桂林电子科技大学认知无线电与信息处理教育部重点实验室 桂林 541004)
1 引言
随着时代和科技的发展,复杂网络逐渐衍生成为一门交叉度很高的综合学科,涉及到金融学、社会学、生态学、政治学、数学物理、系统科学、生物学等学科[1~3],复杂网络的应用领域也越来越广泛,已经在购物系统、推荐系统[4]、地球物理、生物医疗、金融模型[5]、天气预测、生物系统[6]、社交网络等方面具有非常广泛和深度的应用,复杂网络已经成为数据科学的基石[7],能够充分揭示各种事物的本质和演化规律[8~13]。复杂网络具有各种各样的性质,其中关于复杂网络的重分形特性是研究的热点,引起了众多学者的深入研究,目前已经有学者对复杂网络在单独考虑节点权重和边权重时所具有的重分形性质进行研究,但同时综合了节点权重和边权重的复杂网络的重分形性质则缺少相应的研究,本文即是基于水平可视图算法,利用改进的沙箱算法对分形布朗运动时间序列映射而成的同时包含节点权重和边权重的可视网络进行计算,探究网络的重分形维数与节点权重和边权重之间的关系。
2 水平可视图算法
目前,将时间序列转化为可视网络从而研究复杂系统的性质已经成为了众多研究者的热点,并且已经在股票交易、外汇汇率、能量扩散、病情诊断、飓风预测等领域得到了广泛的应用。Lacasa L等[14]提出了自然可视图(Natural Visibility Graph,NVG)算法,NVG算法指如果时间序列x(tk)中任意两个节点i、j之间存在的所有中间节点均在i、j两点连接直线之下,则将i、j连接起来,否则i、j之间没有连接边,即:

这样便可将时间序列x(tk)映射成为一个可视网络。B.Luque等[15]基于NVG算法提出了水平可视图(Horizontal Visibility Graph,HVG)算法,即如果时间序列x(tk)中任意两个节点i、j之间的所有节点值均小于x(ti)、x(tj),则节点i、j之间存在连接边,否则不存在,即:

3 改进的沙箱算法
目前的研究结果表明复杂网络主要具有无标度、小世界以及自相似三大特性,尤其是自相似特性,目前已经成为复杂网络的研究热点。目前针对揭示复杂网络重分形维数的算法研究,已经得到了越来越多的学者的关注。2017年Liu等[16]针对加权网络中不同边权重数量过少时难以计算网络分形特性这一弊端,提出了一个提高的盒覆盖算法,即从网络最小权重值d0到网络直径d等间隔设置盒子的半径,然而对于Liu提出的算法,通过一系列计算发现,Liu所提算法存在大量的计算浪费。因为盒覆盖算法的最终核心思想是寻找到合适的作为线性拟合区间的盒子半径集r并得到相应最小覆盖网络所需盒子数,所以并没有必要从最小边权重值d0到网络直径d设置线性步长总数,只需要抓取核心适合于作线性拟合部分的盒子半径即可。改进的算法如下:
1)根据网络规模设置采样节点个数,对网络的最短路径矩阵进行采样。
2)对每个采样节点与其他所有节点之间的距离进行等间距的采样。
3)根据采样结果,选择最短路径值最集中的区间作为盒子半径范围。
4)在所选择的半径范围内等间距设置间隔,并将此作为各个盒子的半径以传统沙箱算法计算网络的重分形维数。
以H=0.1的分形布朗运动时间序列基于HVG算法映射所生成的边加权指数取k=-3的加权网络为模型,将改进的盒覆盖算法与Liu所提出的算法进行比较。图1中,改进的算法的盒子半径是从1~1500,间隔为1,一共1500个盒子半径,而Liu所提算法以盒子半径间距为10取一共有69164个用于覆盖网络的盒子半径。从图1可以看出,改进的算法可以很好地保留最后最适宜进行线性拟合的盒子半径区间,去掉了头尾的不必要区间,将盒子半径个数缩小至Liu所提算法的数十分之一左右,证明了改进的算法在保持计算精度的前提下大大地提高了计算的速度。

图1 改进的沙箱算法与Liu所提算法相比较
4 实验结果分析
本文中,利用Matlab软件自带的“wfbm”函数生成分形布朗运动时间序列,将Hurst指数H设置为0.1,此时的分形布朗运动具有较强的自相似性,节点总数N设置为5000,一共生成100个分形布朗运动时间序列。对于每一个时间序列,利用HVG算法生成相应的可视网络。
边权重定义为相连接的两个节点的函数值之差的绝对值,即:
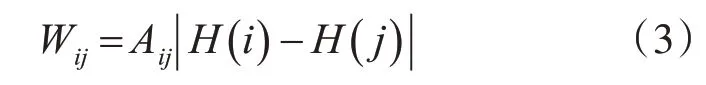
节点权重定义为
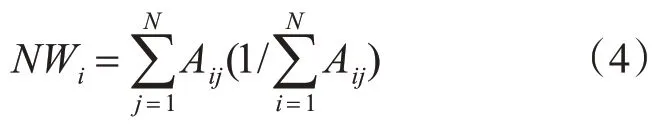
在本文中,对于H=0.1所生成的100个节点加权和边加权网络均利用改进的沙箱算法,计算各个网络的广义分形维数D(q),其中q从-10~10,间隔为1,最后对100个网络的广义分形维数取平均值<D(q)>,即为H=0.1下分形布朗运动映射而成的综合节点加权和边加权的可视图网络的广义分形维数D(q)。图2为最后ln(<[M(r)]q-1>)/(q-1) 与ln(r)进行线性拟合,网络选自100个可视网络中的一个,q取0,2,4,6,8,10。
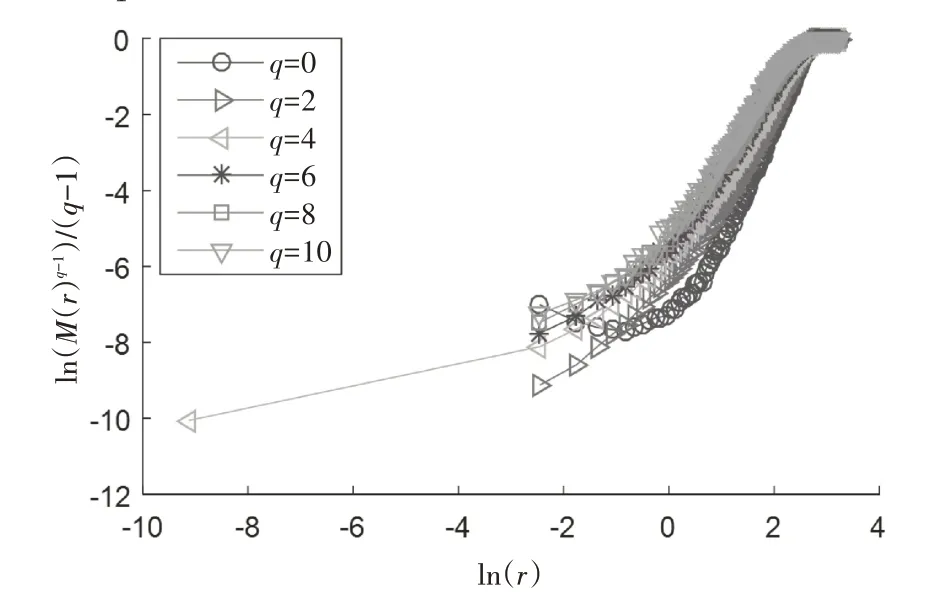
图2 最后不同q时的线性拟合
H=0.1时,利用改进的沙箱算法,对分形布朗运动基于HVG算法映射而成的节点加权和边加权的100个可视网络计算得到的平均广义分形维数<D(q)>如图3所示。与Yu等[17]通过沙箱算法对H=0.1时分形布朗运动映射而成的原始可视网络相比较,此时的广义分形维数D(q)整体有所增大,但下降趋势基本保持一致,依然具有明显的重分形特性。

图3 同时包含节点和边权重时的广义分形维数D(q)
图4为H=0.1时,分形布朗运动基于HVG算法映射而成的可视网络随边权重值变化时,广义分形维数D(q)的变化情况,均取自100个网络的平均值。从图4(a)可以观察到,在-1 ≤k ≤1的范围内,D(q)随着边权重系数k的增加而增加,在-1 ≤k ≤0.5时,增加部分集中在q>-3部分,q<-3部分基本不变;在k从0.5增加到1的过程中,增加部分主要是q<0部分,q>0部分保持平稳。从图4(b)可以观察到在k从1增加到2的过程中,D(q)随着k的增加而增加,在q>0部分,则颠倒过来变成随着k的增加而减小;在k从2增加到3的过程中,D(q)则是随着k的增加而逐渐减小的,尤其是q>0的部分,迅速减小至接近于0。

图4 广义分形维数D(q)随边权重变化情况
图5为节点权重变化时D(q)的变化情况。从图5可以观察到,此时的广义分形维数D(q)随着k的增加而逐渐减小,但整体的变化情况很小,远没有边权重变化时D(q)的变化大,也由此可以说明网络的广义分形维数D(q)主要与节点是否被盒子覆盖有关,而与节点本身的权重值关系不大。
5 结语
本文主要通过利用改进的沙箱算法,对由H=0.1时的分形布朗运动基于HVG算法映射而成的同时包含节点权重和边权重的可视网络进行广义分形维数D(q)计算,分析在同时包含节点权重和边权重的情况时,复杂网络的广义分形维数D(q)的变化情况。结果表明,复杂网络边权重对于复杂网络重分形特性的影响很大,且重分形特性的变化与边权重系数的变化之间是不存在线性关系的,而节点权重对于复杂网络的重分形特性的影响则较之边权重小很多,可以说基本不受其影响。对于本文中所发现的这些重分形特性,与其背后所对应的网络所具有的拓扑结构和其他统计特性之间是否存在联系与如何定量分析两者之间的联系,值得进一步深入研究。

图5 广义分形维数D(q)随节点权重变化情况
