改进粒子群算法在舰船备件配置优化问题中的应用∗

（中国人民解放军92771部队 青岛 266000）

1 引言

2 舰船备件配置优化

舰船备件配置可以看作一个复杂的多约束、非线性组合优化问题，其优化过程复杂，计算量大，收敛速度较慢，且容易陷入局部最优解。

2.1 可靠度要求

可靠度是指装备在一定的条件下，在规定的时间内，完成要求功能的概率。装备可靠度是时间的函数，通常记为R（t）。设T为装备寿命的随机变量，则可靠度函数为

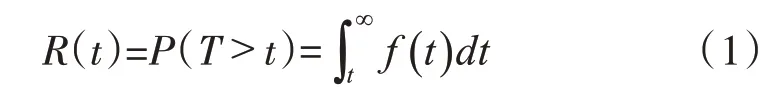
装备失去本该具有的功能就是失效。装备从开始工作到失效前为正常工作时间T，称为装备寿命［4］。用F（t）表示寿命T的分布函数，则：

系统装备整体可靠度由所有基本单元可靠度决定，本文将整个系统视作串联。设系统装备由m个部分组成，第i部分有n个备件，则该装备系统的第i个部件的可靠度：

只有串联系统所有相对独立部分均工作正常时，整个系统才能正常工作，所以可用下式对系统可靠度进行表达：

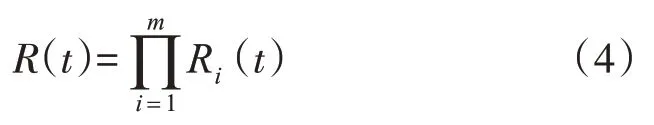
2.2 费用要求

系统备件的供应受到资金的影响，所以备件优化问题必然受到费用的约束。尤其是在战时，费用问题更为突出明显，有限的资金如何发挥最大的作用对任何一样物资的供应都有着极其严格的要求。

2.3 模型的建立

记M为备件种类，xi为第i种备件的存储数量，向量V=［xi x2…xM］即表示了一个储备方案；ci为第i种备件的单价，C0为可用于备件储备的总费用，R0为武器系统任务可靠度最低门限值。C=f1(V)为最终用于备件储存的总费用，R=f2(V)为装备系统任务可靠度优化结果值，依部件之间结构关系运算求得［5］。一般备件优化模型可分以下几类。

在新时代机遇与挑战并存背景下，广东瑞丰生态环境科技股份有限公司专注土壤修护事业，走出了属于自己的发展之路。为了共商土壤修护大计，构建基层土壤修护服务模式，共同推进绿色生态文明建设，11月18日，“千秋伟业激昂前行”中国首届基层土壤修护服务体系发展论坛暨2018瑞丰生态（集团）第五届“未来之星”VIP客户联盟财富峰会在安徽黄山召开。

模型1：目标函数是任务可靠度，约束条件是备件的经济指标，也就是满足费用约束情况下，将任务可靠度最大化。

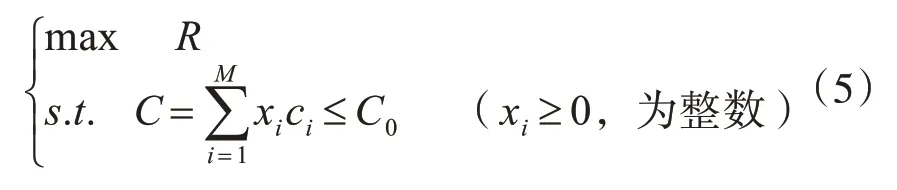
模型2：目标函数是费用，约束条件为系统任务可靠度，也就是达到任务可靠度约束条件下，将所需费用降到最少。

模型3：目标函数是任务可靠度与费用之间比值，约束条件为系统任务可靠度与费用，也就是资金有限的情况下，实现对可靠度最基本的要求［6～7］。

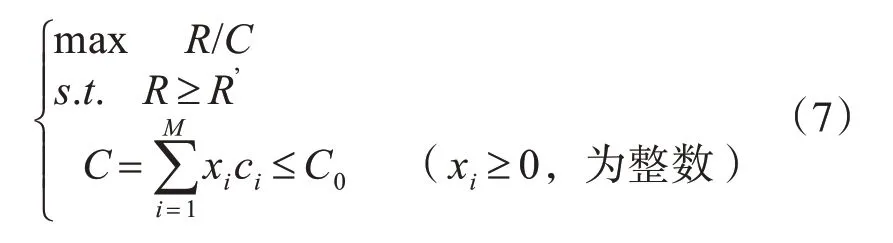
3 改进的粒子群算法

粒子群算法（PSO）是Kennedy和Ebernart博士在1995年时所提出的随机寻优算法［8］。PSO算法在求解优化函数时，具有较好的寻优能力，但基本的PSO算法非常容易陷入局部最优，产生较大的误差，所以对PSO算法进行一定的改进就显得非常重要。PSO算法的具体参数主要有微粒群个数、惯性权重ω、学习因子等。

3.1 惯性权重的改进

惯性权重ω作用是可以实现粒子全局与局部搜索能力之间的平衡。迭代初期，全局搜索能力是粒子必须具备的，把惯性权重的值设置高点可以保证在全局范围内大步长搜索。在迭代后期，粒子需要在小范围内集中搜索，所以为使局部的搜索能力得到提升，可以调低惯性权重值。显然，在进化公式中，惯性权重是非常重要的因素。1998年，惯性权重线性减少这一概念由Y.shi等学者提出，也就是线性递减策略，惯性权重用下式表示：

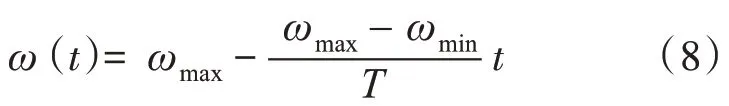
其中，ωmax、ωmin分别表示最大、最小惯性权重值［9］。

3.2 学习因子的改进

学习因子c1和c2的值在PSO算法中起到反映粒子向个体历史、全局最优位置学习能力的作用，其设置的合理性对粒子之间的学习交流和寻优能力影响较大，过高设置会使粒子脱离搜索区域，偏低设置导致粒子搜索范围减小。1999年，M.Clerc给出学习因子值为2.5的想法，基于此，Suganthan等在考虑线性递减策略后改进更新公式：

其中，cmax表示最大的学习因子；cmin表示最小的学习因子［10～12］。

3.3 改进粒子群优化算法CLPSO

在基本粒子群优化算法研究中，粒子会同时向个体最优值pbest和全局最优值gbest学习。但gbest并不能保证是最优的，这导致粒子可能始终无法再靠近最优解的范围内寻优，最终产生粒子陷入局部最优的问题。文献［13］提出一种Comprehensive Learning Particle Swarm Optimizer（CLPSO），它使用了一种新的学习策略，可以提高种群的多样性，并能有效解决粒子在多峰上问题。在该学习策略中，粒子的速度公式被定义为

其中fi=［fi(1),fi(2),fi(3)…fi(D)］表明个体最优值所对应的粒i，pbestfi(j)j表示任何一个粒子的pbest。在每一维中，设定一个随机数rand，根据rand值的大小判定粒子的pebst的值。若rand值大于概率pci，那么其相应的维度将会遵循自己的pbest，若小于概率pci，那么维度值将会学习其他粒子的pbest。其中，概率pci有如下定义：

4 舰船备件配置优化实例及分析

舰船某系统有四个类型的重要构件［13］，其单价与故障率如表1所示。

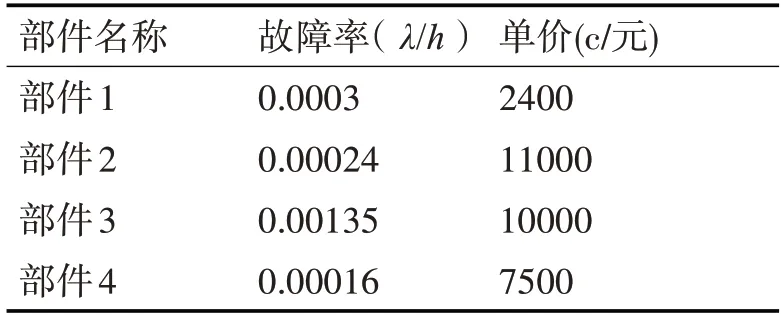
表1 系统备件参数表

其中，费用限制为99000元，工作时间为1450h，系统可靠度至少达到0.85。采用模型3，即备件优化模型为

s.t.R≥0.85，C≤99000，xi≥0，为整数

4.1 试验过程及结果

设定改进粒子群算法参数如下：群规模选择30个粒子，精度为10-5，进行10次仿真试验，c1=c2=2.5，惯性权重ω=0.5，迭代数取100，学习概率取式（11）。CLPSO算法执行程序如下。

1）对粒子群进行初始化，随机将各粒子散布在搜索空间、对粒子初速度进行设定，且明确所有粒子适应值和最佳群体gbest。

2）任意取m维粒子朝着gbest进行学习，根据学习概率P，明确剩余D-m维学习粒子，Flag(i)=0,End Fori。

3）For i=1to S，如果Flag(i)不小于最佳粒子更新阈值，则任取m维粒子朝着gbest进行学习，根据学习概率pci。明确剩余D-m维学习粒子，Flag(i)=0,End。

4）根据式（10）和粒子最大速度求得所有粒子速度，对粒子当前位置进行更新，明确pbest，If pbest不变，则Flag(i)=Flag(i)+1,End If 。

5）End Fori，明确gbest最佳群体，到满足设定终止条件为止［14～16］。

统计数值测试结果与进化代数后分析可得如表2。不难看出，尽管CLPSO算法与Mx-MIMIC都能确定最优配置，同时实现系统可靠度最基本的要求，但相较于Mx-MIMIC算法，CLPSO算法求取的最优配置可以省4000元。在进化代数上，CLPSO算法为25，Mx-MIMIC算法为64，表明CLPSO算法进化速度更快，仿真试验效率得到了很大的提高。

表2 测试结果对比

4.2 可靠度约束条件对结果的影响

在上述实验中，发现可靠度R0的增大，能尽可能地提高费用利用率。设系统约束可靠度R0从0.9开始，按0.01递增，直到0.99，共10组参数。分析得出，系统可靠度越大，费用利用率也就越高，由于可靠度无法不限制地增大，最大到0.9561为止，结果如表3所示。

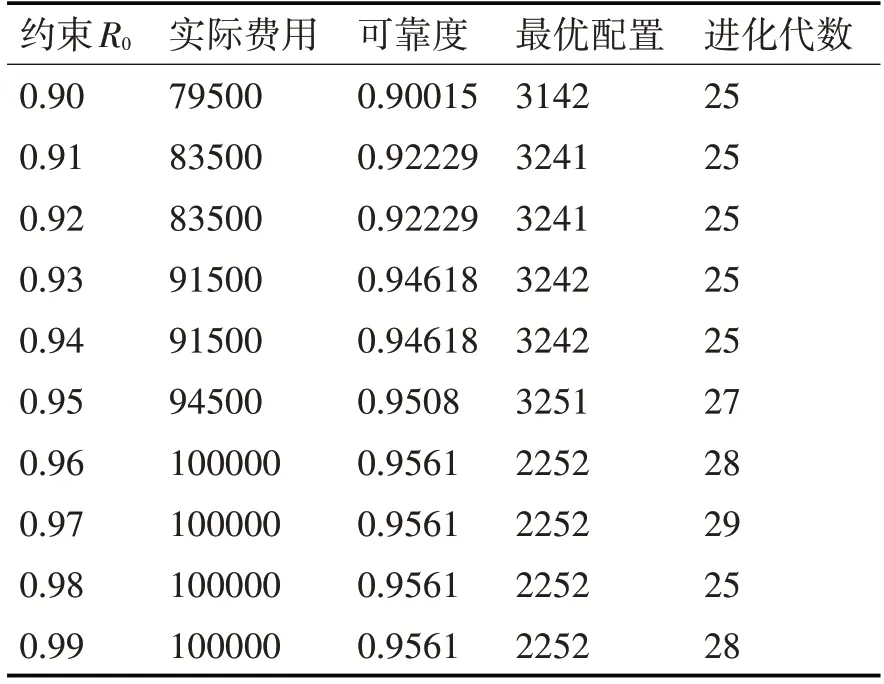
表3 可靠度约束条件对结果的影响

5 结语

本文采用将系统任务可靠度与费用之间比值作为研究问题的目标函数，可靠度、费用作约束条件的模型研究舰船备件配置优化问题，采用改进粒子群算法CLPSO对该问题进行求解，验证其可行性，并与Mx-MIMIC算法进行对比证明其优越性。在下一步研究中，可基于对各备件保障效能参数的分析研究，探索纳入各方面保障效能参数，以综合效能度量为目标构建备件优化配置模型。