基于粒子群算法的多机无源定位系统优化布站∗

2021-04-04

计算机与数字工程 2021年3期

（海军航空大学烟台 264001）

1 引言

由于无源定位技术具有隐蔽性好，可定位距离远，定位方法和手段较多等优点［1］，各军事强国在此方向上投入了大量的科研精力。特别是多机无源定位技术在近几年的研究中得到了突飞猛进的发展。

文献［2］和文献［3］系统介绍了多机无源定位技术基本原理以及可用的定位体制。文献［4］对影响多机定位精度因素进行了细致分析，推导出存在站址误差与速度误差的克拉美罗下限（CRLB）。多机无源定位系统定位精度的影响因素主要有系统内各机位置误差，目标辐射源位置误差，到达时间（到达角）误差以及其它测量误差，然而在一定海空战场环境下，当其他误差一定的情况下，系统内各机位置布局以及其误差对定位系统精度影响相对较大。文献［5］对多机几种典型布站的定位精度进行了仿真分析，得出了四站星型布站的GDOP等高线图，并进一步研究了基于典型布站的二次自主规划布站高精度定位，但是并没有给出自动寻优的布站策略。文献［6］介绍了基于遗传算法的无源定位系统优化布站的方法，解决了针对空间中某一目标或区域定位系统最佳布站问题，但是算法收敛较慢，对于快速定位环境并不适用。所以研究多机无源定位系统优化布站策略对于有效提升无源定位效率和精度具有重要意义。

2 多机无源定位系统定位精度的GDOP

几何精度稀释GDOP（Geometric Dilution of Precision，GDOP）是表征无源定位系统定位精度的一种指标，通过对比GDOP值高低来衡量定位精度，GDOP值越大，定位精度越低，反之越高［7］。文献［8～10］给出了GDOP详细的推导过程，并对影响因素参数进行了分析，应用其结论，给出多机GDOP推导公式。

多机无源定位系统共有N架飞机，其中S0为主机，S1，S2，S3，…Sn为辅机，目标辐射源为T，其中Si=（Xi，Yi，Zi），i=｛0，1，2，3，…n｝，目标T=（X，Y，Z）。其定位方程为

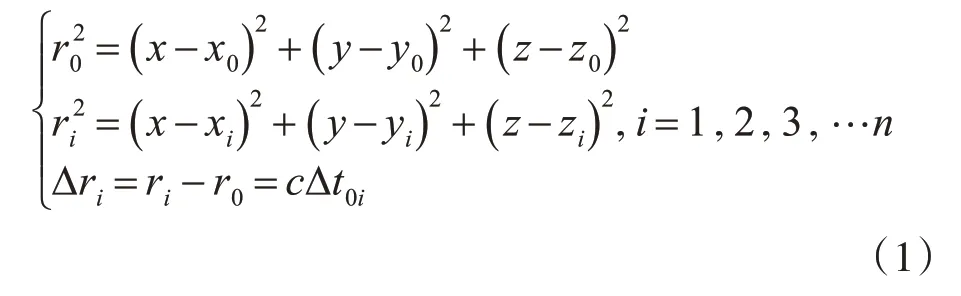
式中，r0表示目标到主平台的距离，ri（i=1，2，3，…n）表示目标到副平台的距离，Δri表示目标到主平台与到各副平台的距离差，c表示电磁波的传播速度，Δr0i表示信号到主平台与到各副平台的时间差。

对式（1）的等式两边微分，得下式：

式中：

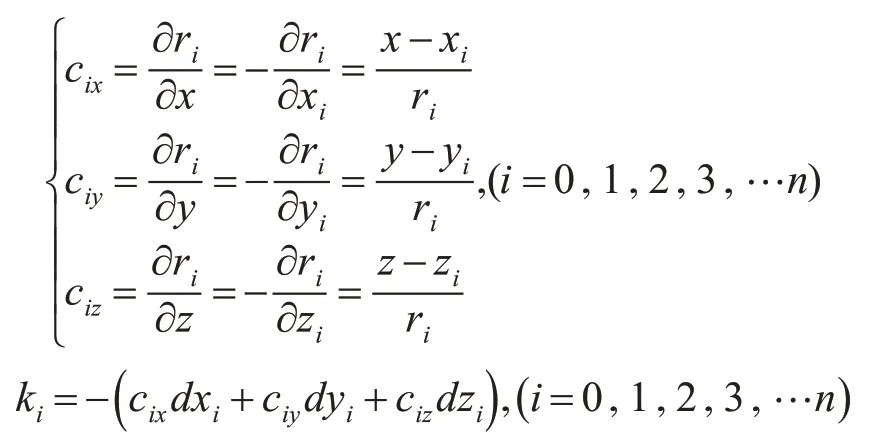
将式（2）转换成矩阵表达式为

整理上式，则定位误差估计值如下式：

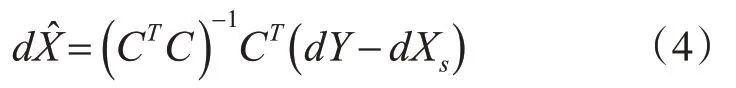
求解得到协方差：

所以定位误差在x，y，z三个分量的方差为

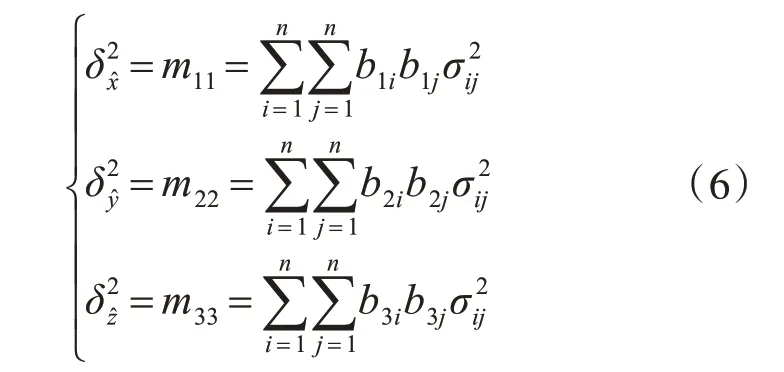
则多机时差无源定位精度GDOP表达式为

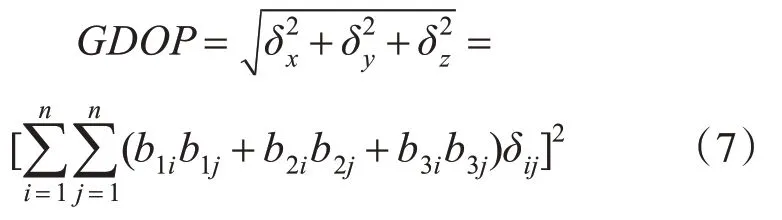
3 基于粒子群算法的最优布站方法

粒子群算法（Particle Swarm Optimiztion，PSO）是一种有效的全局寻优算法，最初由美国学者Ken⁃nedy和Eberhart于1951年提出［11］。它是基于群体智能理论的优化算法，通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。粒子群算法具有进化计算和群体智能的特点，通过个体间的协作与竞争实现复杂空间中最优解的搜索，个体的每一个粒子按照下面的算法进行自身速度和位置的更新。

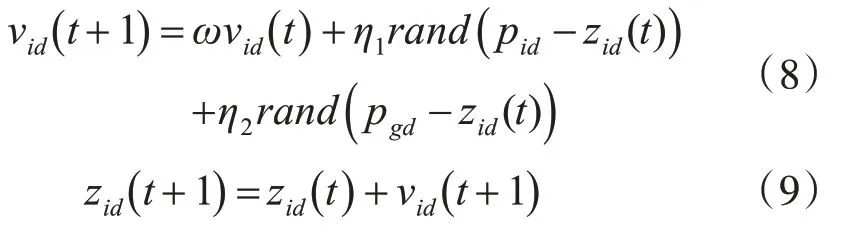
式中，Vid表示第i个粒子某时刻速度，d表示粒子所在空间的第d个坐标分量，Pid表示自身最优解，Zid表示某时刻粒子所处位置即所求问题的一个解，Pgd表示全局最优解，ω是惯性权重，其取值范围一般为0.1～0.9之间，η1、η2为加速因子，其取值范围为0～2，且为保证收敛η1+η2≤4。

3.1 粒子群算法的基本流程

粒子群算法具有自行起步的特点，给定粒子的维度和初始种群的规模，可以实现随机自动初始赋值，通常流程为粒子群初始化、适应度值计算、局部最优选择、全局最优选择、粒子速度与位置进化（产生新粒子）以及迭代步进输出最优结果［12］。如图1所示。

1）种群初始化（设定粒子群规模，最大迭代次数并对其赋值）；

2）通过适应度函数计算每一个初始粒子在当前状态下的适应度值；

3）对计算出的适应度函数值与最优值（当前最优与自身最优）进行比较，如果出现最优则取代前一次最优，并且用新粒子取代前一次粒子；

4）将各个粒子的最优适应度值与所有粒子最优适应度值比较，如果出现最优，则用最优取代全局最优，同时记录最优适应度值对应粒子；

5）完成上述计算之后判断是否达到迭代次数或者精度要求，如果没有则按照式（8）和（9）更新粒子状态，从步骤2）继续计算直至满足条件；

6）满足条件结束，输出最优粒子与最优适应度值。

图1 粒子群算法流程图

3.2 最优布站策略

前文已推导了多机TDOA定位算法定位误差的GDOP公式，最优布站方法是利用粒子群算法的基本原理搜索解算定位系统对某一区域内目标定位平均GDOP最小的多机位置。

其最优布站策略是在确定的定位站数量基础上，当定位系统在某一规定区域内时，针对空间中某一区域目标求解平均的定位误差的GDOP最小，利用粒子群算法对规定区域进行迭代搜索解出最优的各站位置。

3.3 参数设定与适应度函数选取

仿真中选取无源定位系统站数为N（N=4，5，6），由于各站由空间三坐标表示，则单个粒子维度为3×N，粒子群规模选取20，则初始化种群规模为3×N×20。为利于算法收敛，选取ω=0.7298，η1=2，η2=2。

适应度函数值是评价种群中个体优劣的重要指标，是保留和淘汰个体的判断准则，对于多机无源定位系统选取表征定位精度指标的GDOP值更有利于实现布站优化，GDOP值越小定位精度越高。文中选取定位系统对某一区域内目标定位平均GDOP值作为适应度函数。其表达式为

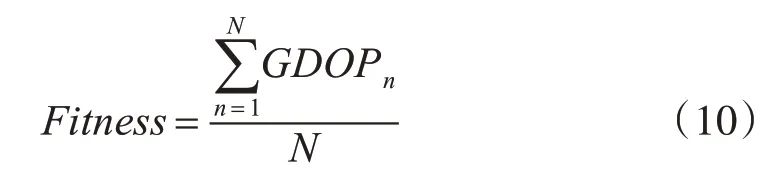
其中N代表定位区域中所选点的个数，GDOPn代表各点对应GDOP值。

图2 空间4站无源定位优化布站结果

4 仿真与结果分析

4.1 空间4站无源定位优化布站仿真分析

假定定位目标区域为X=［-200，200］，Y=［100，200］，Z=0，主机固定S0=［0，0，4］，各辅机位置上限为［20，20，5］，下限为［-20，-20，3］，粒子群算法各参量依据3.3节设定，空间4站无源定位优化布站结果如图2所示。

图4 空间6站无源定位优化布站结果

表1 粒子群算法与典型布站结果对比

基于以上仿真条件，空间4站基于粒子群算法最优布站各站坐标为S0=（0，0，4）km，S1=（20，20，5）km，S2=（1.0574，-20，3）km，S3=（-20，20，3）km，目标区域最小GDOP均值为1177。4站典型布站［5］各站坐标为S0=（0，0，4）km，S1=（20，20，3）km，S2=（0，-20，3）km，S3=（-20，20，3）km，目标区域最小GDOP均值为6692。图2（a）表示目标区域GDOP均值随迭代次数变化关系，随迭代次数增加GDOP均值减少并收敛于稳定值，说明了粒子群算法的可行性，图2（b）表示最优布站各站位置与目标区域关系，图2（c）和图2（d）分别表示典型布站和最优布站的GDOP等高线图，从两图对比中可以明显看出最优布站对目标区域的GDOP分布优于典型布站。

4.2 空间5站无源定位优化布站仿真分析

仿真条件与4.1节相同，空间5站无源定位优化布站结果如图3所示。

基于以上仿真条件，空间5站基于粒子群算法最优布站各站坐标为S0=（0，0，4）km，S1=（20，20，5）km，S2=（20，-20，5）km，S3=（-20，20，3）km，S4=（-20，-20，3）km，目标区域最小GDOP均值为650。5站典型布站［13］各站坐标为S0=（0，0，4）km，S1=（20，20，5）km，S2=（20，-20，5）km，S3=（-20，20，5）km，S4=（-20，-20，5）km，目标区域最小GDOP均值为1014。图例分析同4.1节。

4.3 空间6站无源定位优化布站仿真分析

仿真条件与4.1节相同，空间6站无源定位优化布站结果如图4所示。

基于以上仿真条件，空间6站基于粒子群算法最优布站各站坐标为S0=（0，0，4）km，S1=（20，20，5）km，S2=（20，-20，5）km，S3=（-20，20，3）km，S4=（-20，-20，3）km，S5=（20，-20，3）km，目标区域最小GDOP均值为601。典型布站［14］各站坐标为S0=（0，0，4）km，S1=（20，20，4）km，S2=（20，-20，4）km，S3=（-20，20，3）km，S4=（-20，-20，3）km，S5=（20，-20，3）km，目标区域最小GDOP均值为800。图例分析同4.1节。