聚焦知识本质，发展数学核心素养

郭建芬

[摘要] 运算律是数学运算的主要性质，反映了运算的规律性。学习运算律不仅是为了计算简便，更为重要的是发展学生对数与运算意义的理解。通过呈现“乘法分配律”磨课历程与思考，体现小学数学运算律教学应厘清运算本质，培养学生数学学习能力，发展数学核心素养的教学思路。

[关键词] 知识本质;数学核心素养;乘法分配律

“乘法分配律”是苏教版义务教育教科书四年级下册的学习内容。教学时不仅要重视结论的归纳，拉长探究过程，凸显儿童立场，同时要引导学生多角度感悟其中的思维逻辑和数学内涵，实现学科核心素养的切实提升。

一、首次教学——显露缺憾  陷入尴尬

片段一 创设情境，初步感知

师：（出示班级领取篮球的情境图）从中你获得了哪些数学信息？

生：四年级有6个班，五年级有4个班，每个班领5个篮球。

师：根据这些条件你能提出哪些数学问题？

生1：四年级和五年级一共领多少个篮球？

生2：四年级比五年级多领多少个篮球？

生3：五年级比四年级少领多少个篮球？

（教师引导学生列综合算式解决问题）

算法一：（6+4）×5=10×5=50（个）

算法二：6×5+4×5=30+20=50（个）

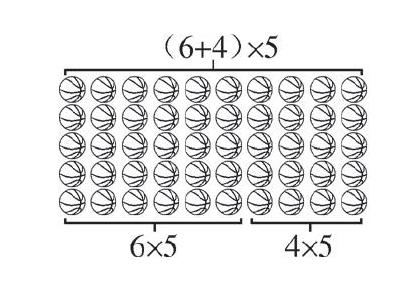
生4：6×5表示四年级6个班一共领多少个篮球，4×5表示五年级4个班领多少个篮球。

生5：（6+4）表示两个年级一共有10个班，再乘5就表示四、五年级一共领多少个篮球。

师：（呈现篮球图）仔细观察这两种方法你发现了什么？

生1：他们两个算式中都有一个5，结果相等。

生2：每个班都领5个篮球，既可以两个年级合起来算，也可以两个年级分开来算。两种方法的结果相等。

师：两个不同的式子，结果却相等，你知道其中的道理吗？

生1：左边是两个年级合起来算，右边是两个年级分开来算，结果都是50。

师：你能从乘法的意义角度去解释吗？

生2：6×5表示6个5是多少，4×5表示4个5是多少，合起来就是10个5。所以结果相等。

师：还有同学想说说其他的解释吗？（学生沉默）

思考：运算律是伴随数学运算的自然存在。教学中创设具体生活情境，引导学生自主提出问题，分析两种方法的解题思路，在解决问题的过程中通过观察比较，结合具体的数量关系初步发现两种方法结果相等。当引导学生解释左右两边式子结果为何相等时，很少有学生能够脱离情境，从乘法的意义等角度进行表述，结果就是方法比较单一，学生思维受限。

片段二 探究规律，深入理解

师：（6+4）×5=6×5+4×5，两种解法运算顺序不同，但却得出了一样的结果，会不会是巧合呢？

生1：再举几个例子。

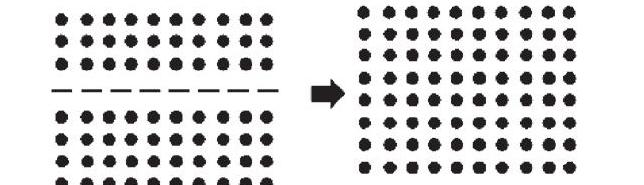
师：我们借助点子图来研究。仔细观察你获得了哪些数学信息？

生2：每排10个点子，有这样的8排。每列有8个点子，有这样的10列。

师：下面请小组合作讨论分法，可以横着分，也可以竖着分，然后选择其中的一种分法写在导学单上，通过说理或算一算的方法判断两个式子结果是否相等。

（学生合作交流后，各组汇报活动结果）

生1：1×10+7×10=（1+7）×10

生2：2×10+6×10=（2+6）×10

生3：3×10+5×10=（3+5）×10

生4：4×10+4×10=（4+4）×10

师：等式两边的式子结果为什么相等？

生1：我们是通过计算的方法判断的。

生2：点子数一共就是80个，所以结果一定相等。

师：大家还能从别的角度说说吗？

生3：1个10加7个10合起来是8个10;2个10加6个10合起来是8个10;3个10加5个10合起来是8个10;4个10加4个10合起来是8个10。

师：仔细观察你有什么发现？

生：不管怎么样分，左右两边合起来都是8个10。

师：现在没有点子图你能独立写出几个这样的式子吗？然后用自己的方法判断左右式子两边是否相等。

（教师引导学生写等式，归纳乘法分配律，并用字母表示这个运算律）

思考：这个环节中，教师首先让学生比较左右两边式子的相同点与不同点，引导学生关注数据特征，关注结构特征。然而，在利用点子图进行验证时却陷入了窘境：一些学生能分割点子图，却又不能根据点子图写出相应的算式;一些学生纠结于怎么分割点子图，却忽视了对左右两边结果为何相等的解释;更有一部分学生不知所措。究其原因，一方面是上述片段学生说理时没有切身体验，理解停留在表面，比较肤浅，同时在验证环节提供了同一幅格点图，学生的思维被禁锢，对乘法分配律的结构特征感知仍然比较模糊，结论的得出牵强而生硬，教学陷入尴尬。

总体来看，首次执教暴露出诸多缺陷，一是因为临时借班上课，前面的加法、乘法运算律学生还没有学，缺乏对运算律的认知经验，学生似乎一直被拽着走，学习的主体性、主动性不够;二是借助点子图进行举例验证时，学生过多地把注意力放在“怎么分”上，左右两边算式的结构特征得不到凸显，乘法分配律的模型建构与预设效果相去甚远;三是学生的演绎推理能力等没能得到历练和发展。

二、再次实践——无缝对接 水到渠成

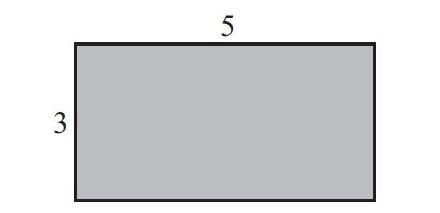
针对以上问题进行对应的调整：一是学习加法、乘法的交换律和结合律相关知识，帮助学生积累相关活动经验和学习方法，同时课前增设复习环节，勾连新旧知识，为课堂有效探索和迁移做好铺垫;二是立足学生，注重说理，关注多元表征，增设让学生用自己喜欢的方式去解釋两边算式结果为什么相等这一环节，激发学生的潜能;三是进一步丰富学习素材，增加了长方形面积图，借助几何直观，更好地帮助学生发现其结构特征，为构建数学模型提供支撑。再次执教，教学内容和教学形式都做了相应的调整和对接，给足学生探究的时间和空间，聚焦知识本质，发展学生核心素养。

片段一 激活旧知，产生联想

师：（依次出示四张图片）前面我们已经学习了加法、乘法的运算律，看着这些图你们想到了哪些运算律？用字母怎么表示？

思考：通过四幅图直观呈现，数形结合，激活学生对已经学过的加法、乘法运算律的相关认知，同时引发猜想“在乘法和加法之间是否存在运算律”。如此一来，就激发了学习好奇心，引发学生探索欲望。

片段二 聚焦本质，深入理解

1.注重对比，质疑释疑

师：同一情境，两个不同的式子，它们的结果为什么会相等呢，你能进一步说明其中的道理吗？想一想我们在说理的时候通常会采用什么方法？

生1：结合生活实际讲故事。

生2：画图。

生3：举例子。

师：（引导学生用喜欢的方法去解释说明）生活中买衣服、桌椅等经常会成套购买，用讲故事的形式解释这个道理，合情合理。

生1：假如买一条裤子需要6元，一件上衣需要4元，买5套这样的衣服可以分开买也可以合起来买，都是5件上衣和5条裤子的价格，所以需要的钱是一样的。

生2：我是用线段图表示的，上面表示6个5，下面表示4个5，一共有10个5。

生3：我用的是画图的方法。竖着看左边表示6个5，右边表示4个5，合起来就是10个5。（6+4）×5就表示10个5，所以结果相等。

师：（演示点子图变成方块图，最后变成长方形）这幅图的意思看懂了吗？你能解释一下为什么两个算式的结果相等？

生：6×5表示红色长方形的面积，4×5表示蓝色长方形的面积，加起来是大长方形的面积，6+4的和表示大长方形的长，再乘以宽就是大长方形的面积。

思考：借助生活经验和几何直观，是小学阶段学生理解数学知识的两种辅助手段。学生对于运算律的理解不应是肤浅的、表面的，而要用他们自己的方式有创造性地表达对乘法分配律的理解和描述。引导学生用自己的方式去解释或说明道理，就为学生个性化思考和表征提供了舞台。他们或根据生活实际讲故事，体会它的合情合理，或根据乘法的意义给出解释，或根据长方形面积计算去说明理由。从不同角度展开推理与联想，加深了学生对乘法分配律的理解，同时也向演绎推理跨出了可喜的一步。

2.数形结合，探索举证

师：猜想一下其他算式中是否也具有这样的特征呢？它们的结果也相等吗？

生1：有的，我觉得它们的结果都相等。

师：能这么快下结论吗？接下来我们该怎么办？

生2：为时过早，我们可以再举点例子去验证一下。

师：（借助几何画板演示）下面我们借助图形玩一个“超级变变变”游戏，同桌两人合作，选择下面的菜单按键变化图形，一人报出算式，另一个人记录，同桌交流并判断两个算式结果是否相等。（学生借助平板电脑，点击变化图形，写出相应算式，验证探究）

师：写出来的两个算式结果都相等吗？怎么判断两个式子的结果是否相等？

生：通过计算发现，左边的长方形面积加右边长方形面积都等于大长方形面积。

师：仔细观察这些算式，你又发现了什么？

生1：每次的数都在变化，但它们的结果都相等。

师：想一想结果为什么会相等呢？

生2：因为左边的长方形面积加右边长方形面积都等于大长方形面积。

师：谁还能从两个算式的联系来解释一下呢？

生3：我发现右边的加起来就是左边括号里的和。

师：你的意思就是几个相加合起来就是相乘之积，为你的发现点赞！现在不看图，你能独立再举出这样的几个例子吗？想一想举例时注意些什么？

生4：举的例子要有代表性。

生5：（3+0）×3=3×3+3×0。

师：想象一下这个例子是怎样的一幅图？

生6：只有一个长方形。

师：那两边的计算结果相等吗？

生：（齐）相等。

师：这是一个特例，但同样能说明两边结果相等。

生7：我发现（2×5）×2不等于2×2+5×2。

师：这个例子有问题吗？

生8：这个例子不符合算式的特征，括号里应该改成2+5，两边就相等了。

师：现在你们觉得还需要再举例吗？你找到其中的规律了吗？怎么说明这个规律？

生9：用字母表示。

……

片段三 串联整合，内化提升

师：想一想我们以前接触过乘法分配律吗？（出示图片，引导学生计算图的周长，找出其中蕴含的乘法分配律）

师：在计算中我们曾遇到过乘法分配律，你还想到了哪些运算中蕴含着乘法分配律？

……

三、磨课思考

《义务教育数学课程标准（2011年版）》指出，数学活动经验的积累是提高学生数学素养的重要标志。[1]教学中通过创设情境，引导学生经历发现问题、提出问题、分析问题和解决问题的全过程，同时通过沟通实际问题，感知数学模型;把握规律内涵，理解数学模型;探究结构特点，建构数学模型;串联知识体系，内化数学模型，层层递进，让乘法分配律的结构特征进一步清晰，知识本质得以凸显。

1.多元表征，深化知识本质

数学学科教学，必须对教学内容所经历的过程以及使用的方法作一定的阐述。在认识抽象的数学原理或规律时，仍需以具体形象的事物或图片作为载体，借助几何直观来完成向抽象思维的过渡。[2]因此，在学生结合具体数量关系得出算式两边相等后，教师直击知识本质，引领学生深入探寻知识背后的道理。激发学生创意，激活数学思维，用生活实例、电子图、线段图等辅助手段，用数、形、事、理相结合的形式解释说理，用多元表征解释乘法分配律。同时，巧妙引入几何模型长方形面积图，构建“面积模型”。最后，通过“创意变变变”，超越表面形式的模仿，引领学生触及数学规律最核心的内在结构——数形结合，达成不同表征系统的相互转化，实现数学抽象、逻辑推理等学科素养的发展。

2.有效勾连，内化知识本质

“要理解事物就要用联系的观点来看待它”，而“要对知识形成深刻的、真正的理解，意味着学习者所获得的知识是结构化的、整合的，是相互关联的”。[3]学生认识的乘法分配律其实在以前的学习中早已有了孕伏。教师在教学中和学生边回忆、边解释、边联想，让新旧知识得以勾连，知识体系得以建构，促进数学理解从零碎走向结构化，进一步体会乘法分配律应用的广泛性、普遍性，积累活动经验，感悟思想方法，内化知识本质，提升数学核心素养。

[参考文献]

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大學出版社，2011：46.

[2]张奠宙，巩子坤，任敏龙，等.小学数学教材中的大道理——核心概念的理解与呈现[M].上海：上海教育出版社，2018：17-19.

[3]李艳.聚焦本质 深度理解——“3的倍数的特征”教学实践与探索[J].小学数学教育，2018，280（22）：71-72.