水平轴风力机复合材料叶片结构特性有限元分析

张 旭，张孟洁，李召暄，李 伟

（1.天津工业大学天津市现代机电装备技术重点实验室，天津 300387；2.天津城建大学能源与安全工程学院，天津 300384）

1 引言

风力机发电是清洁能源主要生产方式，也是当今世界能源生产的主要潮流。作为风力机发电的关键部件，风力机叶片一直是研究者们的热点研究对象[1-3]。叶片设计过程中，对叶片进行结构性能分析可以有效地了解设计参数对于叶片结构的影响，以提高风力机叶片结构性能。

国内外学者在风力机叶片的结构性能分析方面取得了一些进展。文献[4]提出一种叶片结构设计，并通过有限元方法对叶片进行了强度分析，根据分析结果验证了该结构设计。文献[5]对34m的复合材料叶片数值模拟并进行失效测试。文献[6]运用有限元方法研究了同一几何外形不同铺层方案下叶片的模态特性。文献[7]利用有限元法，针对某一叶片的叶根进行了强度分析。文献[8]使用ANSYS 软件分别计算了单个叶片与整机中叶片的静动态特性。但是，对于有限元方法的基础验证，众文献中几乎没有提及。

应用理论和有限元法分析了拉压、弯曲、扭转基本变形下的结构性能，并通过结果对比验证了应用数值计算过程的正确性。在构件基本变形解析验证的基础上，利用有限元软件建立了叶片参数化模型，计算了叶片固有频率，重力、风载作用下的静态响应，为大型叶片结构性能分析提供依据。

2 构件结构性能分析对比

层合板是复合材料结构的基本结构形式，由各单层复合材料沿厚度方向叠合而成的多层材料。通过层合板理论和蔡吴强度准则[9]，可以推导得到构件复合材料各层的应力分量以及强度比值的求解公式。

2.1 应力分量和强度比求解公式推导

2.1.1 应力分量计算公式

层合板的应力应变关系式，如式（1）所示（式中ε0为中层面应变，k为层合板的曲率）。

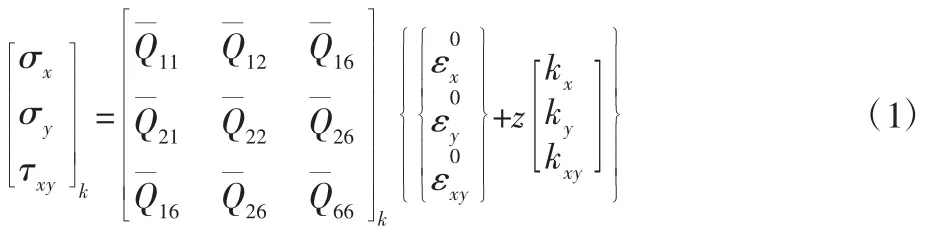
在已知层合板材料的属性以及具体铺层情况下可以得到正轴刚度矩阵［Q］，通过坐标转换得到偏轴刚度矩阵中层面应变 ε0和曲率k可以通过式（2）求解。

式中：N、M—构件所受的力和力矩；A、B、D—构件整体刚度矩阵；等式左边分量在拉压时Nx取定值，弯曲时Mx取定值，其他分量为零。将应变和刚度矩阵带入应力应变关系式从而求解每层的纤维向应力分量。

扭转变形的应变求解与拉压、弯曲变形的应变求解过程不同，坐标系选择柱坐标系，圆筒仅受扭矩T，应变只考虑中层面应变。扭转变形下的应变求解公式，如式（3）所示。

式中：D—圆筒外直径；ti—铺层层数。

将应变值ε 带入式（1），得到正轴应力分量，正轴应力分量带入式（4）得到纤维向应力分量。

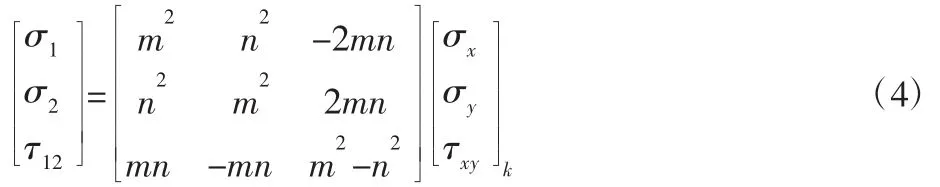
2.1.2 强度比计算公式

根据蔡吴强度准则推导得到强度比R的计算公式：

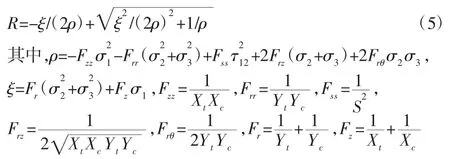
将纤维向应力带入强度比公式，可以得到铺层各层强度比，判断构件能否满足强度要求，并得到强度裕度。

2.1.3 构件模型及数值算例

叶片的约束和受力情况类似于悬臂梁，因此选择梁进行拉压、弯曲变形分析；叶片属于薄壁壳体结构，因此选用薄壁圆筒进行扭转变形分析。选择长L=20mm，宽B=1mm，高H=1mm 的长方体模型，如图1 所示。选用碳纤维T300/934 作为铺层材料，铺层角度与顺序依次为 90°，0°，0°，90°，每层厚度为 0.25mm，分别受拉力10N，弯矩MX=5N；薄壁圆筒的几何尺寸半径r=50mm，长为100mm，总厚度为1mm，如图2 所示。铺层参数与梁相同，受扭矩1250N·M。

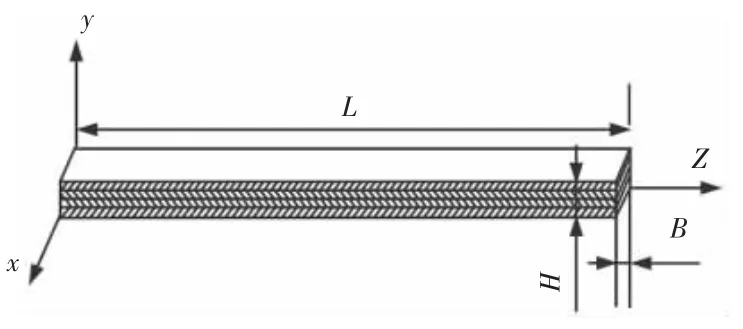
图1 复合材料梁几何模型Fig.1 Composite Beam Geometry Model

图2 复合材料薄壁圆筒几何模型Fig.2 Composite Thin-Walled Cylinder Geometry Model

将构件模型的相关参数数据带入解析式公式，得到三种基本变形下的解析解，如表1 所示。

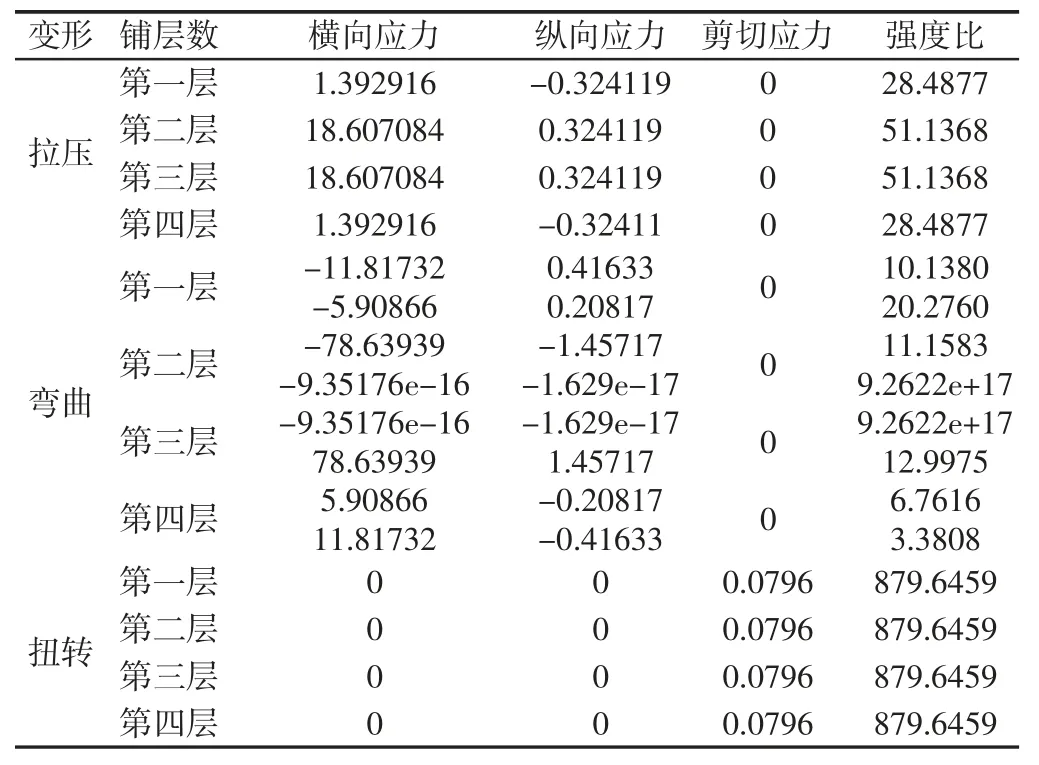
表1 基于解析法的应力和强度比结果Tab.1 Stress and Intensity Ratio Results Based on Analytical

2.2 构件基本变形有限元分析

建立与理论计算时几何、铺层参数相同的构件有限元模型。拉压变形时，复合材料梁z=0、y=0 的一端施加对称约束，在z=20的一端施加拉力FX=10N，模拟复合材料梁拉压变形，如图3（a）所示。弯曲变形时，复合材料梁z=0 的一端施加固定约束，在z=20的一端添加y方向转动的耦合位移并在这一端施加弯矩MY=5N，模拟复合材料梁弯曲变形，如图3（a）所示。扭转变形，对薄壁圆筒z=0 的一端施加固定约束，在z=100 的一端施加轴向的耦合位移约束，并在该处的各个节点施加周向力fy=25N，即相对应为扭矩1250N·M，如图3（b）所示。对模型计算并提取各层的应力分量和强度比。得到三种基本变形下的应力分量和强度比值，如表2 所示。

图3 构件有限元模型Fig.3 Finite Element Model of Component

表2 基于有限元方法的应力和强度比结果Tab.2 Stress and Intensity Ratio Results Based on Finite Element

将解析和有限元法的结果进行对比计算得到误差。三种基本变形情况下的应力分量误差分别为0.00149%、0.0027%、1.5553%，强度比误差分别为0.2182%、0.2362%、0.9824%。发现两者误差都很小，结果可以视为一致。结果说明应用ANSYS 程序的建模过程，几何模型铺层，以及约束和载荷定义均正确，所得应力分量和强度比数值结果合理。

3 2MW 风力机叶片有限元建模

采用2MW 风力机复合材料叶片作为研究对象，叶片长度31m，最大弦长3.219m，根据文献确定叶片各截面参数，包括翼型型号、弦长、扭角等[10]。

3.1 坐标转换

叶片截面翼型的空间坐标点数据，需要通过以下坐标变换公式进行转换。坐标变换公式，如式（6）所示。

式中：θ—扭角；r—叶片展向长；c—截面弦长。

在已知各截面原始参数的情况下，应用翼型空间坐标变换式，得到叶片各截面翼型实际空间坐标。将截面翼型坐标数据，以创建关键点K的命令保存至TXT 文件。

3.2 叶片有限元建模

应用ANSYS 软件，建立风力机复合材料叶片模型。使用APDL 语言导入关键点，并将各截面翼型的上下翼型的关键点连接成样条曲线，将曲线作为引导线蒙皮生成光滑曲面；选取距离翼型前缘的每个翼型的0.24c和0.54c处作为腹板位置添加腹板；选择shell181 单元对叶片通过赋予截面属性的方法定义各面铺层的材料类型、铺层角度、铺层厚度以及铺层顺序，同时设置网格尺寸进行网格划分，得到完整复合材料叶片模型，如图4 所示。

图4 叶片有限元模型Fig.4 Blade Finite Element Model

4 风力机叶片的结构性能分析

4.1 叶片的模态分析

对叶片根部进行固定约束，进行模态分析，得到前六阶固有频率以及振型，如表3 所示。模态振型图，如图5 所示。

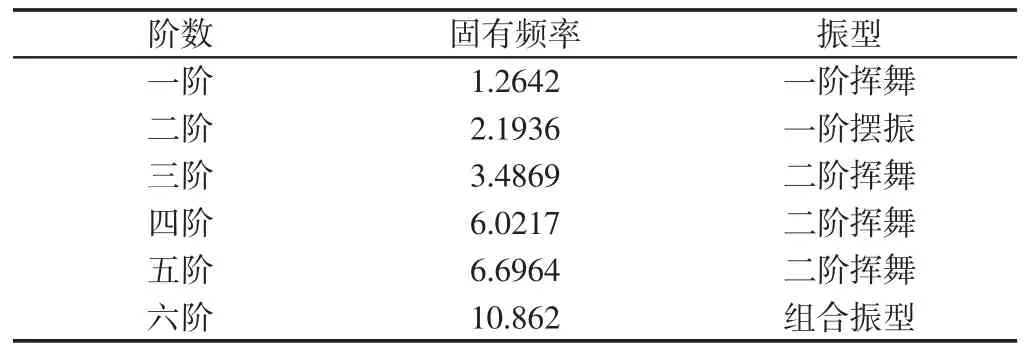
表3 前六阶固有频率和振型Tab.3 Natural Frequency and Mode Shape of the First Six Orders

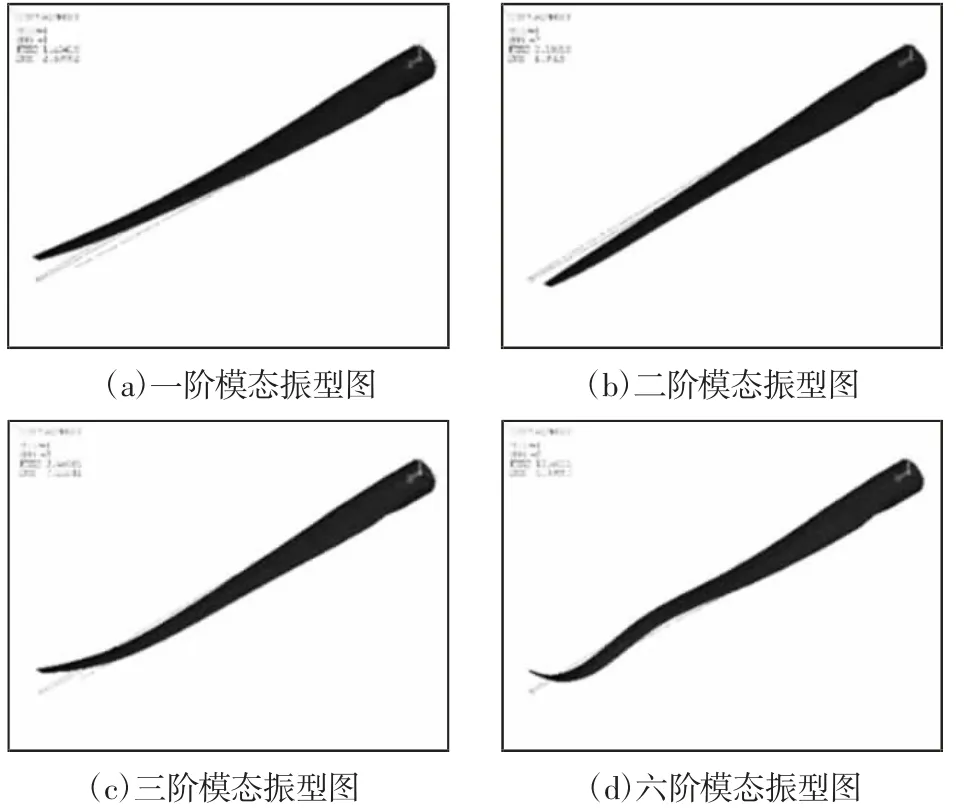
图5 模态振型图Fig.5 Modal Mode Diagram

2MW 复合材料叶片额定转速为（12～19）r/min，转化为旋转频率为（0.2～0.318）Hz，为了防止叶片发生共振，要求其固有频率远离其旋转频率。所建模型一阶固有频率最小，但大于额定转速下的叶片旋转频率的3 倍以上，符合安全要求。

4.2 叶片的静力分析

4.2.1 重力作用下的静力分析

把叶片叶根进行固定约束，对叶片施加自身重力，计算叶片在静止状态下受自身重力影响的位移与应力分量，如图6、图7所示。

图6 叶片位移分布图Fig.6 Blade Displacement Distribution

图7 叶片应力分布图Fig.7 Blade Stress Distribution

叶片在重力作用下的最大位移为124.021mm，最大应力为29.1494MPa，通过对位移和应力图的分析，发现受力方向最大位移发生在叶尖处，最大应力位于翼型与叶根交界处的部位，与叶片真实受重力情况相符。

4.2.2 风载作用下的静力分析

风力机叶片的主要受力方式就是受风载荷，随着叶轮旋转所处位置会发生变化，叶片所处高度不同风速也不同，所受风载荷也不同。选取叶片的三个主要位置叶片作为研究对象。不同高度风速对叶片产生的压力[6]：

选择塔架与叶片相交部分为参照点，H0为参照点高度即塔架高度，V0为参照点风速（即额定风速），Z为叶片上各点所处高度。对位于塔架高为62.5m 的三个位置的单叶片施加额定风速在12.5m/s 的风载，得到在风压下的最大位移和最大应力。叶片在不同位置的最大位移和应力，如表4 所示。

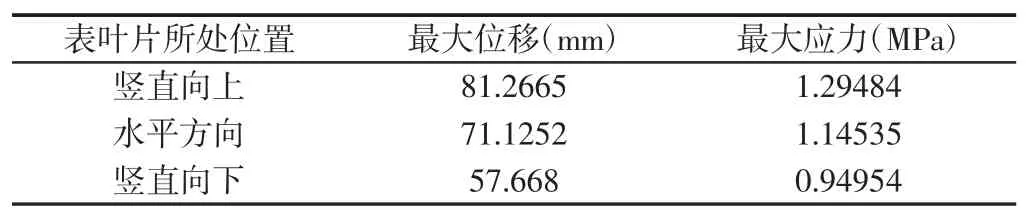
表4 不同位置额定风载下的最大位移和应力Tab.4 Maximum Displacement and Maximum Stress Under Wind Load at Different Locations

叶片在额定风速载荷作用下的最大位移为81.2665mm，最大应力为1.29484MPa，且均发生在叶尖处，此时叶片位于竖直向上方向位置，位移和应力分布，如图8、图9 所示。

图8 叶片位移分布图Fig.8 Blade Displacement Distribution

图9 叶片应力分布图Fig.9 Blade Stress Distribution

随着叶片所处位置的变化，叶片所受最大应力和最大位移的数值也会改变，但最大位移均位于叶片的叶尖部分。最大应力位于叶中部分。

5 结论

在构件基本变形解析验证的基础上，通过有限元软件建立了MW 级水平轴风力机复合材料叶片模型，计算了叶片固有频率，以及在重力、风载作用下的静态响应，研究可知：

（1）对复合材料梁的拉压、弯曲变形以及薄壁圆筒的扭转变形这三种基本变形应用解析法和有限元法进行应力和强度比求解，并对结果进行比较分析，验证了应用ANSYS 程序的几何建模，铺层方法，以及约束和载荷定义的正确性。

（2）对叶片进行结构性能分析，叶片的一阶固有频率大于额定转速下的叶片旋转频率的3 倍以上，符合安全要求；受重力作用时，最大位移发生在叶尖，最大应力位于翼型与叶根交界靠近叶根处的部位；受风载时，叶片最大位移发生在叶尖，最大应力位于叶中部分。