基于并行策略的改进混合粒子群算法及其应用
2021-04-02陆凤仪于浩洋徐格宁
陆凤仪,于浩洋,徐格宁
(太原科技大学机械工程学院,山西 太原 030024)
1 引言
优化的过程就是将一个需要解决的问题抽象为一个数学模型,并使用优化算法求其最大值或最小值。优化算法可分为梯度优化算法和非梯度优化算法。梯度优化算法指向最优点的搜索方向明确,收敛速度快,对于复杂多峰问题容易陷入局部最优,前提条件是目标函数连续且可导,在实际工程问题中目标函数往往是离散、不可导。非梯度优化算法缺乏指向最优点的搜索方向,搜索过程更为随机,但收敛速度较慢,容易跳出局部最优,不依赖目标函数的连续、可导性,更符合工程要求。
粒子群算法(PSO)是当下最流行的非梯度优化算之一,被广泛研究与改进。目前对粒子群算法的改进分为对粒子群算法自身的改进和混合其他算法改进粒子群算法。在粒子群算法自身的改进方面:文献[1]中提出一种自适应的方法,根据其性能和距离,确定了每个粒子在不同维度上的惯性权重,提升了粒子群算法解决方案质量。文献[2]针对可靠性优化问题,提出一种没有速度和参数的NSC-PSO 算法。文献[3]提出了3 种非线性的惯性权重,来提升粒子群算法的质量和收敛速度。上述文献对粒子群算法自身的参数进行改进,挖掘粒子群算法的潜力,有效地提升了粒子群算法针对某些目标函数的性能,但难以克服高维度复杂优化易陷入局部最优的局限性。在混合其他算法改进粒子群算法方面:文献[4]借鉴了差分进化算法的交叉和选择操作,生成指导向量提升优化结果质量和求解效率。文献[5]提出一种粒子群算法与实数编码遗传算法相结合的混合算法,很好的平衡了混合算法的开发能力与探索能力。文献[6-8]使用模拟退火算法(SA)作为PSO 的本地搜索机制,帮助PSO 跳出局部最优。借鉴其他算法可以很好地改善PSO本身的一些难以解决的缺陷,但会增加算法的复杂程度。
就工程实际应用而言,文献[9]使用3S(强度、刚度、稳定性)理论及几何约束构建门式起重机门架优化模型,使用零阶优化方法优化该模型,减小了门架质量。文献[10]使用3S(强度、刚度、稳定性)理论构建通用桥式起重机主梁金属结构模型,提出并使用改进果蝇算法优化,减小了主梁体积。但并没有针对实际情况合理划分网格,圆整后会产生较大误差。
鉴于此,以并行策略为基础,不改变种群规模,独立运行3种算法,每隔n次比较3 种算法,获得当前最优点,并用其替换粒子群算法的种群最优点,利用PSO 算法个体向种群最优靠近的特点,使被替换后的PSO 算法跳出局部最优,提升优化结果的质量。同时,为验证算法的实用性,将其应用在10t~32t/31.5m 系列化的桥式起重机主梁金属结构轻量化设计中。
2 算法原理
2.1 粒子群算法(PSO)
粒子群算法(Particle Swarm Optimization)由Kennedy 和Eberhart 于1995 年提出,是一种模拟鸟群觅食行为的智能算法[11]。鸟群在整个搜索食物过程中,鸟群相互沟通,信息共享,让所有鸟知道种群最优位置,每只鸟通过种群最佳位置和个体最佳位置修正飞行的方向向量,最终鸟群聚集到食物附近。粒子群算法中有NP个粒子,粒子有速度向量V和位置X两个属性,在搜索空间中随机生成NP个初始位置X和速度向量V。
在迭代过程中,每个粒子按式(1)生成下一代粒子的速度向量和位置:
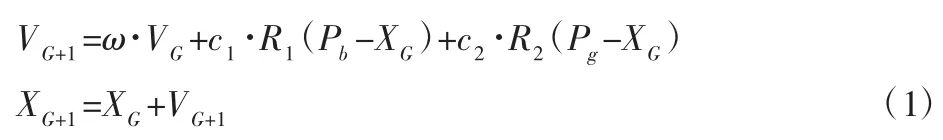
式中:ω—惯性因子;
c1、c2—加速因子,为正常数;
R1、R2—[0,1]之间的随机数;
Pb、Pg—粒子当前最优位置和种群最优位置;
G—已完成迭代次数。
为了防止粒子飞出搜索空间,对粒子的速度和位置进行约束,如式(2)、式(3)所示,算法流程,如图 1 所示。

式中:Vmax、Xmax—粒子速度和位置的上限;Vmin、Vmin—粒子速度和位置的下限。
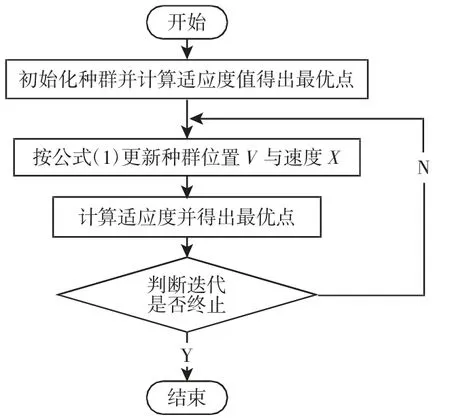
图1 粒子群算法流程图Fig.1 PSO Flow Diagram
粒子群算法鲁棒性好,易于实现,收敛速度快,但在解高维度的多峰问题时容易陷入局部最优,广泛应用于非线性规划、路径规划、汽车生产[12]等领域。如何在粒子群算法寻优过程中平衡探索能力和开发能力对算法的全局收敛尤为重要。
2.2 差分进化算法(DE)
差分进化算法(Differential Evolution),由Rainer Storn 和 Kenneth Price 于1997 年提出[13]。差分进化算法源于遗传算法,其基本思想是利用当前种群个体间的差异重组得到中间种群,然后子代个体与父代个体竞争获得新一代种群。差分进化算法中个体数量为NP,在搜索空间随机生成NP个位置向量,种群个体位置向量为其中,D—优化目标函数的维度;G—种群经过G次迭代;i—种群中的第i个个体,1≤i≤NP。
首先,种群位置向量根据式(4)进行突变操作,得到个体变异位置向量Tij。

式中:r1、r2、r3—[1,NP]内互不相等的随机整数。
然后对种群位置向量和变异位置向量进行交叉操作,得到个体交叉位置向量Cij,交叉操作,如式(5)所示。
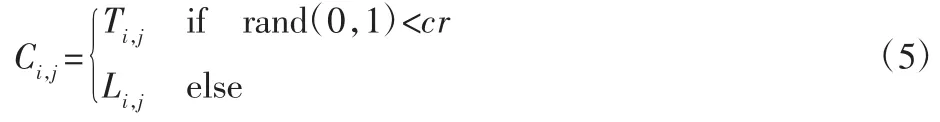
式中:cr—变异算子。
最后进行选择操作,如式(6)所示,得到下一代个体位置向量LG+1,选择操作采用的是贪婪选择策略,差分进化算法流程图如图2 所示。

DE 算法能有效的处理复杂多峰问题,与PSO 算法形成互补。变异算子cr对DE 算法的性能影响很大,合理的设置cr,可以很好的平衡DE 算法的开发能力与探索能力。DE 算法已被广泛的应用于许多实际问题如模式识别、电力优化、特征选择等[14]。
图2 差分进化算法流程图Fig.2 DE Flow Diagram
2.3 人工蜂群算法(ABC)
人工蜂群算法(ABC)是由Karaboga 在2005 年提出[15]。人工蜂群算法来源于蜂群采蜜行为是一种基于群智能的优化算法。人工蜂群算法将蜂群的采蜜行为分为初始化蜜源、放出雇佣蜂、放出观察蜂、放出侦查蜂四部分。在算法迭代开始之前,在搜索空间中随机生成NP/2 个点作为初始化蜜源的位置Si,D},其中,NP为种群规模,i代表第i个蜜源,1≤i≤NP/2,D为蜜源位置的维度,G为当前迭代次数,记录当前蜜源被使用次数的Trail(i)=0;迭代开始后,放出NP/2 个雇佣蜂在蜜源附近寻找新蜜源,观察蜂位置Li由式(7)得出。

式中:d—随机选取的一个维度;
k—随机选取的一个蜜源。
按贪心策略更新蜜源位置,若蜜源位置更新,则Trail(i)=0,若蜜源位置没有改变,则Trail(i)=Trail(i)+1。
然后放出观察蜂,每个蜜源都有一定的概率被观察蜂跟随,每个蜜源被跟随的概率Pi按式(8)计算。

式中:fit(Li)—第i个蜜源的适应度。
使用式(7)在被跟随蜜源附近搜索新蜜源,直至NP/2 个跟随蜂全部放出,并用贪心策略更新蜜源,若蜜源位置更新,则Trail(i)=0,若蜜源位置没有改变,则Trail(i)=Trail(i)+1。
若蜜源满足Trail(i)>limit,其中limit为放出观察蜂的界限,则进行放出侦查蜂操作,在搜索空间中随机生成一个蜜源替代掉蜜源i。limit的值影响算法的开发能力,需设置为一个合适的值,人工蜂群算法流程图,如图3 所示。ABC 算法每次迭代都进行全局搜索和局部搜索,具有很强的全局收敛能力,对目标函数及初值无特殊要求,适应性强。ABC 被广泛应用于结构工程、网络拓扑设计、图像处理等领域[16]。
2.4 混合算法(DA_PSO)
DA_PSO 算法以粒子群算法为基础,采用并行混合策略,将DE 算法和ABC 算法嵌入 PSO 算法中,DE 算法和 ABC 算法在求解高维度、复杂问题,性能出众,使用上述2 种算法的最优点帮助PSO 算法跳出局部最优,并加以探索,可提高优化结果的质量。DA_PSO 算法在每次并行3 种算法迭代结束后设置一个交流区,通过交流区将DE 算法和ABC 算法的求解精度和稳定性传递给PSO 算法,进而得到一种功能强大的算法。交流区分为判断、择优、传值三个部分。DA_PSO 算法的流程,如图4所示。
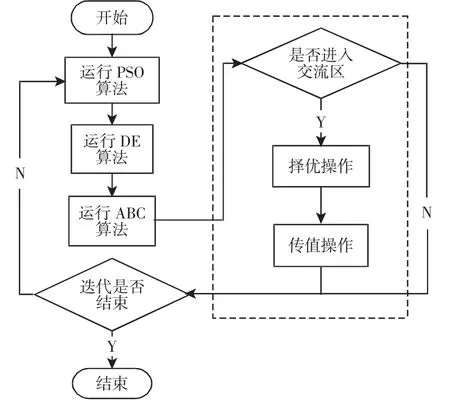
图4 DA_PSO 流程图Fig.4 DA_PSO Flow Diagram
判断部分在每次3 种算法迭代结束后,判断DA_PSO 算法是否进入交流区。判断操作使3 种算法每隔n次交流一次(n的值根据实际情况设置)。
判断进入交流区后,进入择优部分,选出3 种算法运行结果中的最优值和最优点。如式(9)所示。
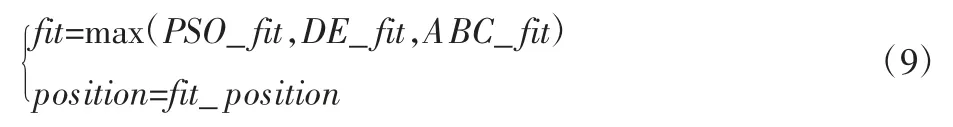
式中:fit—3 种算法运行产生的最佳适应度;PSO_fit、DE_fit、ABC_fit—PSO 算法、DE 算法、ABC 算法的最佳适应度;fit_position—3 种算法的最佳位置(fit对应的位置);position—择优结果。
传值部分的功能是将择优部分产生的最优值,最优点传给PSO 算法,如式(10)所示。

式中:Pg—PSO 算法的种群最优位置。
这个操作会帮助粒子群算法摆脱自身局限,有效提升优化结果的质量。
3 算法测试评价
3.1 测试函数
为测试DA_PSO 算法的性能,使用如表1 所示的5 个函数对混合算法进行算法测试。测试函数f1、f2为单峰函数,f2函数的全局最优点位于一个平滑、狭长的抛物线形山谷内,算法很难辨别搜索方向,f3是二维复杂函数,具有很强的震荡性,很难找到全局最优,f4、f5是典型的非线性多模态函数,具有广阔的搜索空间,是优化算法很难处理的多模态问题。

表1 测试函数Tab.1 Test Function
3.2 测试结果与评价
将上述5 个测试函数分别用PSO 算法、ABC 算法、DE 算法、DA_PSO 算法取合适参数运行30 次,提取均值、最优值、最差值、标准差作为评价参数,其中均值体现算法的精度,标准差体现算法的稳定性。结果如表2 所示,DA_PSO 算法的测试函数迭代次数的均值,如图5 所示。
由表2 和图5 可以看出,PSO 算法在善于解决小范围、低维度优化问题(f2、f3),在大范围、高维度的函数(f1、f4、f5)的测试中得到的结果精度和稳定性都很差;与PSO 算法相反,DE 算法在大范围、高维度的函数(f1、f4、f5)测试中收敛速度快,得到的结果精度高;ABC 算法在各类函数测试中取得优化结果质量较好,稳定性优于DE 算法和PSO 算法。DA_PSO 算法能很好的解决上述所有测试函数,是一种高精度、高稳定性、适应性强的优化算法。
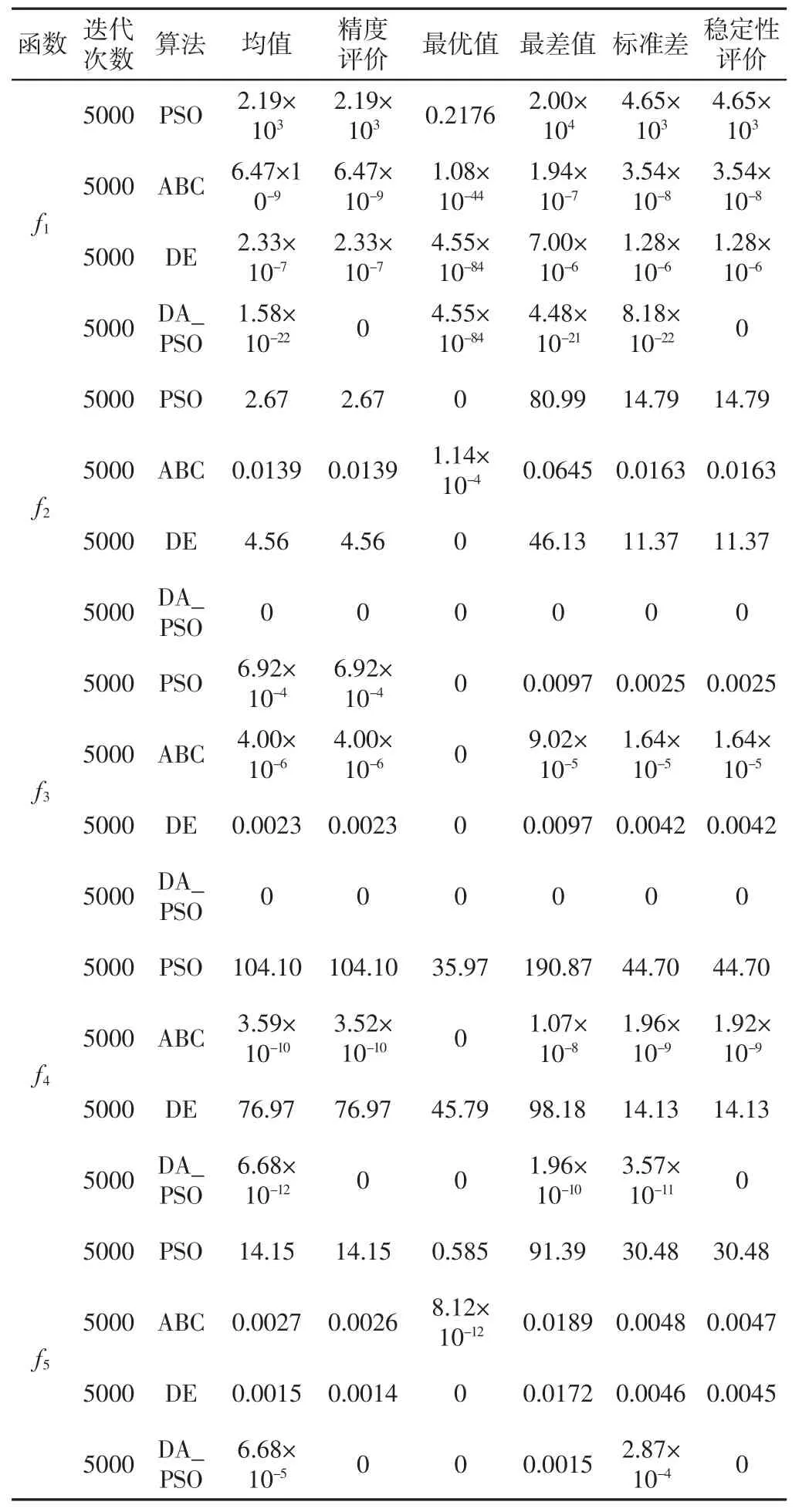
表2 测试结果与评价Tab.2 Test Result

图5 迭代次数的均值Fig.5 Average Value of Iterating Times
DE 算法与PSO 算法擅长领域恰好相反,具有很强的互补性,ABC 算法在解决各类测试函数所表现出的稳定性是PSO 算法和ABC 算法所不具备的。PSO 算法具有很好的鲁棒性,易与其他算法相结合,所有粒子向种群最优位置聚集的功能,可以整合3 种优化算法的信息,并加以探索,在精度方面会表现会优于3种算法单独运行。在稳定性方面,ABC 算法为DA_PSO 算法提供了很好的稳定性,DA_PSO 算法采用并行策略进一步提高算法的稳定性。由于 DA_PSO 算法吸收了 PSO 算法、DE 算法、ABC 算法的特点,DE_PSO 算法的适用范围更广。
结合策略的通用性也很强,不局限于上述3 种算法。这种并行策略只需要其他算法提供给PSO 算法一个当前最优点即可,针对不同的问题可以将DE 算法和ABC 算法换成任意一种合适的算法;而且并行算法的个数也不是固定的。
4 工程实例
4.1 优化模型构建
为进一步验证DA_PSO 算法的实际使用价值,以10t~32t/31.5m 系列化桥式起重机主梁结构为研究对象,使用DA_PSO 算法对其进行轻量化设计。桥式起重机主梁耗费的钢材占成本的30%以上,桥式起重机进行轻量化设计对降低成本具有重要意义。桥式起重机主梁由上、下盖板和主腹板、副腹板焊接而成的箱型梁。桥式起重机结构复杂,工况多变,承受载荷多样,对主梁结构进行合理简化,得出的桥式起重机力学模型,如图6 所示。
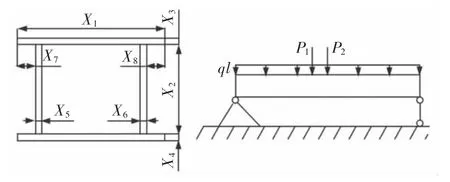
图6 桥式起重机力学模型Fig.6 Bridge Crane Mechanical Model
设计方法采用极限状态法。桥式起重机轻量化设计就是桥式起重机主梁在满足3S(强度、刚度、稳定性)设计要求的情况下,减轻主梁自重(减小箱型梁截面面积)。主梁优化设计模型,如式(11)所示。强度约束条件,如式(12)所示。刚度约束条件,如式(13)所示。稳定性约束条件,如式(14)所示。

式中:f(X)—优化的目标函数(箱型梁截面积);
g1—强度约束条件;
g2—刚度约束条件;
g3—稳定性约束条件;
X1—上盖板宽;
X2—腹板高;
X3—上盖板厚;
X4—下盖板厚;
X5—主腹板厚;
X6—副腹板厚;
X7—轨道侧翼缘外伸;
X8—翼缘外伸。

式中:M—危险截面弯矩;
y—危险点到形心距离;
Ix—主梁截面惯性矩。

式中:Yc—主梁最大变形;
[y]—许用应力[y]=S/1000;
S—主梁跨度。

考虑到主梁的实际制造情况及主梁各参数的几何关系,主梁的几何约束定义,如式(15)所示。

在实际生产中,钢板的厚度(X3、X4、X5、X6)都为整数,为方便划线及备料切割,腹板高(X2)和上盖板宽(X1)以及两侧翼缘外伸(X7、X8)都为10 的整数倍,将整个寻优空间按上述要求划分网格,DA_PSO 算法在网格的节点中寻找最优解。
将寻优空间划分成整数网格,更贴近实际情况,优化生成的结果(箱型梁截面参数)更符合生产制造要求,若迭代完成后再将结果圆整,则会产生较大误差,要么得出非最优解,要么违反约束条件。因此,文本将连续多维的搜索空间离散成整数点,有效的降低了求解问题的规模,保证算法得到最优解。
4.2 优化结果及分析
将起重机箱型梁的跨度S 设置为31.5m,起重量分别为10t,20t,32t。基于DA_PSO 算法的200 次迭代的结果记录在表3 中,目标函数的优化迭代曲线,如图7 所示。DA_PSO 算法任意个体目标函数的优化迭代曲线,如图8 所示。
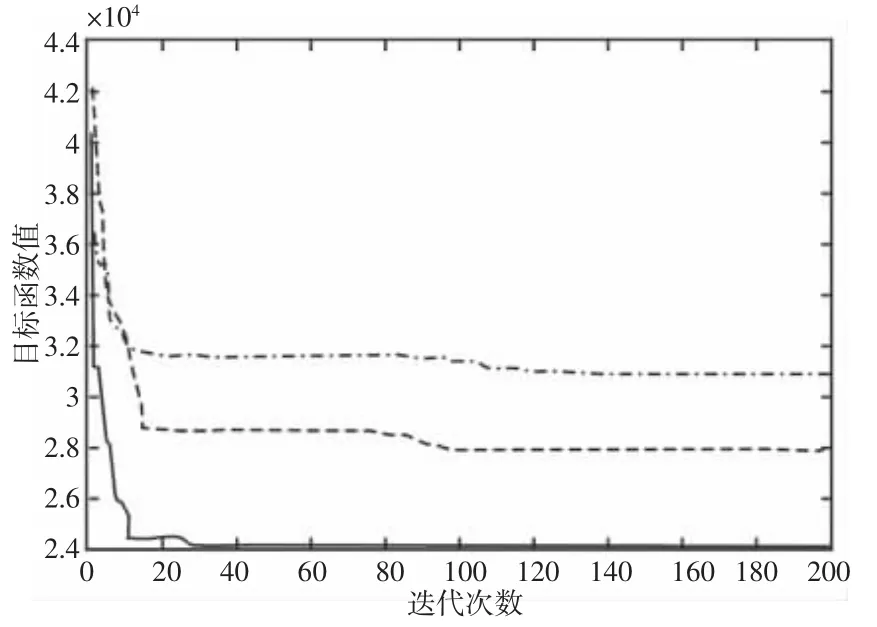
图7 目标函数的优化迭代曲线Fig.7 Optimal Iteration Curve of the Objective Function
通过对图7、图8 的分析发现,DA_PSO 算法在迭代80 次左右达到收敛,能够快速的向最优解收敛,表3 中的数据贴近实际生产情况,易于加工制造。将表3 中起重量为32t 的数据与文献[17]中仿真算例优化后的数据(截面面积为33700mm2)进行对比,主梁截面面积减少6.38%。鉴于以上分析,DA_PSO 算法在几何约束和结构约束的共同作用下,能快速的得到最小截面积且易于生产的箱型梁结构参数,很好的完成了主梁轻量化设计,具有广阔的工程应用前景。
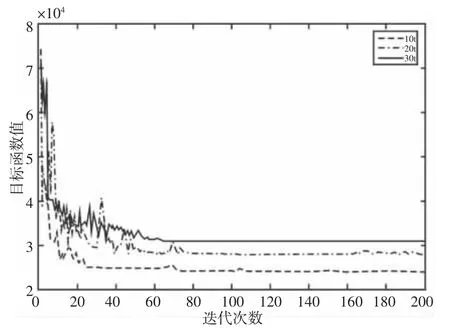
图8 任意个体目标函数的优化迭代曲线Fig.8 Optimal Iteration Curve of Any Individual Objective Function

表3 优化结果Tab.3 Optimization Results
5 结论
对PSO 算法进行研究,发现PSO 算法在解决复杂,多维度问题时,易早熟,陷入局部最优,引入善于解决高维度问题DE 算法和ABC 算法与PSO 算法并行、交流得到DA_PSO 算法,并采用测试函数和工程算例验证DA_PSO 算法性能,得出结论如下:
(1)DA_PSO 算法,吸收了并行的3 种算法的优点,精度高,稳定性好,通用性强,可解决多种问题;由于DA_PSO 算法是并行算法,算法的运算量比单一优化算法的运算量大。
(2)提出了一种混合策略,利用粒子群算法的鲁棒性好,以及向种群最优聚集的特性,针对要解决的问题,将DE 算法和ABC 算法替换成任何其他算法,并吸取其特性,可更改并行算法数量。
(3)针对工程实例合理划分网格,能降低问题规模,得到适合生产制造的优化结果。
