基于可靠性稳健优化设计材料选择
2021-04-02王发展吕勤良郑建校
王发展,吕勤良,郑建校
(西安建筑科技大学机电工程学院,陕西 西安 710055)
1 引言
随着工业化技术的不断革新,大量新型材料不断涌现,它们具有的优质属性越来越多,对新材料的合理设计和利用显得至关重要。材料选择是零件设计的首要任务,同时也是开发新型零件的必要前提。因此通用简便、有效的材料选择方法是机械行业在经济结构转型升级中的重点和关键[1]。
传统的材料选择主要由设计人员依靠自身经验和查阅大量的资料进行选择,这种方式存在认知局限性、材料多样性等其它问题。对此,国内外学者也做有相关研究,文献[2]使用拓扑优化来设计透射的单层周期性变换表面的材料选择;文献[3]提出了灰色模糊逻辑方法在材料选择中的应用;文献[4]利用模糊数学和神经网络的方法对刀具材料选择进行了研究;文献[5]研究了低温支撑结构的材料选择。此外,还有学者对多材料选材做了研究比如采用质量功能部署法、层次分析法和模糊折衷决策等方法探讨了汽车车身多材料的部署[6-8];以及针对不同材料,如磁性磨料、碳纤维复合材料等,总结并提出了回收再利用的主要方法,包括物理法、化学法和能量回收法[9-10]。然而当前的大多数研究都表现有理论性较强,实用性和通用性不够。并且对于机械零部件的设计而言,零件在实际工作中的可靠性[11-13]、稳健性[14]、轻量化才是设计者的首要关注点。因此,提出一种以可靠性稳健优化设计为设计基准的材料选择方法是很有必要的。
本方法综合考虑了零件的设计尺寸,材料属性,极限受力状态等问题,建立了系统的优化数学模型,在保证可靠性一定的情况下,实现结构尺寸的优化,且提高稳健性。随后对不同备选材料设计结果进行分析比较,选出最佳设计材料。
2 可靠性与灵敏度分析
由可靠性设计的摄动法和四阶矩[15]法可知,当已知随机变量的前两阶矩,且随机变量服从正态分布时,利用概率统计中求矩的方法可求得随机变量的三、四阶中心矩。
随机变量X=(X1,X2,…,Xn)T的r阶中心距定义,如式(1)所示。

而在实际设计过程中,往往很难确定随机变量的概率分布,对于非正态分布的情况,就需要通过变换,将非正态的变量转换为正态变量进行处理。另一方面,在无法确定设计变量分布类型的情况下,若能确定设计变量的前四阶矩,也可以使用标准化技术及相应的经验修正公式等近似算法,从而得到设计结构的可靠度。
功能函数Z=g(x)通过标准化技术,如式(2)所示。

得到标准正态随机变量,如式(3)所示。

因此,基于四阶矩与高阶矩标准化技术的可靠性指标β4M,如式(4)所示。

可以获得可靠度的估计量,如式(5)所示。

式中:φ()—标准正态空间的累积分布函数。
在可靠性分析的基础上,求可靠度对随机变量的均值和方差的一阶导和DRFM/DVar(X),得到各随机变量对可靠度的灵敏度,根据灵敏度大小,将设计变量分为主变量和次变量,主变量Y即为优化设计中的约束变量。
3 可靠性稳健优化设计
可靠性稳健优化设计是在可靠性设计的基础上实现零件结构的稳健性和轻量化设计。数学模型[16]表示,如式(6)所示。
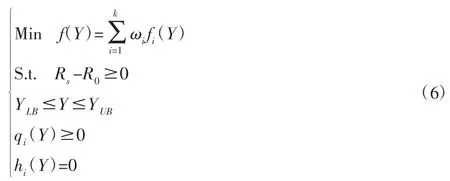
式中:Y—优化设计变量,即为灵敏度分析中得到的对可靠性影响较显著的变量;f(Y)—优化设计的目标函数;ωi—各单独目标函数fi(Y)的权重系数,如式(7)所示;RS—稳健优化设计的可靠度;R0—目标可靠度;YLB、YUB—设计变量的下限和上限;qi(Y)、hi(Y)—不等式和等式约束。
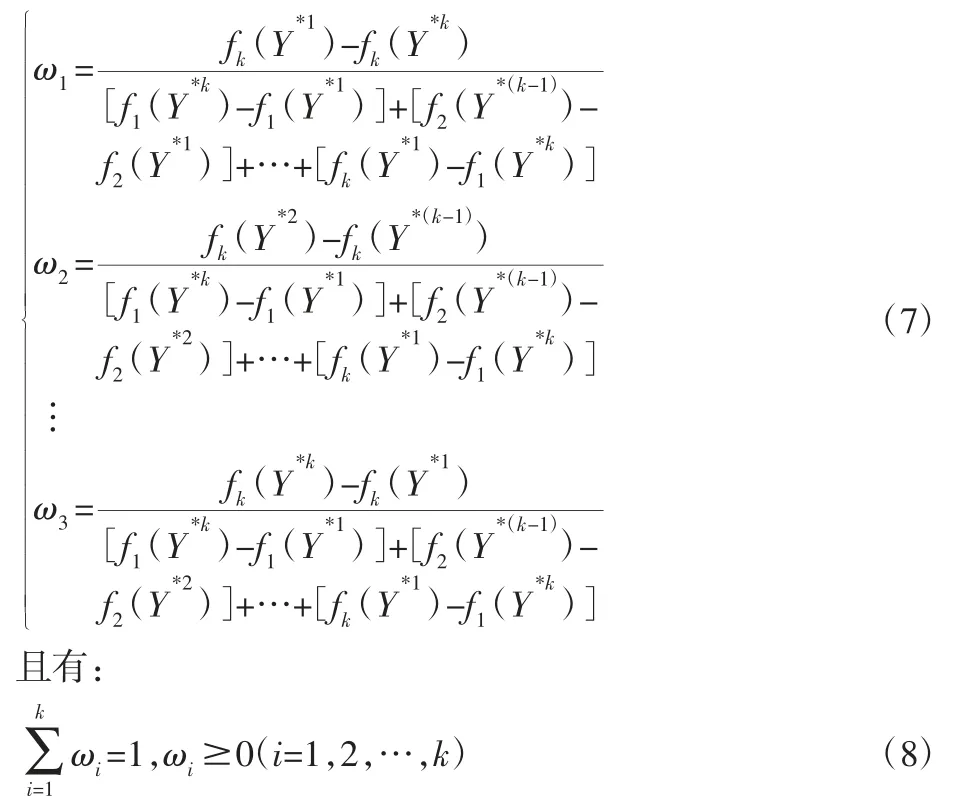
式中:Y*k—第k个目标函数的最优设计点。
4 数值算例
4.1 建立力学模型
某种履带式车辆的主动轮[17],若已知主动轮危险截面处的直径为D1,螺栓孔径为D0,主动轮齿轮厚度为h,主动轮受外界载荷为P,三维模型,如图1 所示。

图1 主动轮三维模型Fig.1 Driving Wheel 3D Model
则由悬臂梁结构模型可以求得在直径D1上,则危险截面处的切应力τ 为:

得到极限状态函数g(Y)为:

式中:r—主动轮材料的强度极限值。
各变量的均值和方差文献[17]中已给出,另外,计算出三、四阶中心矩,数值如表1 所示。

表1 变量的前四阶矩Tab.1 The First Four Moments of the Variables
4.2 建立可靠性稳健优化模型
(1)建立目标函数:①要求主动轮的可靠度对设计变量Y=(h,D0,D1)T均值的灵敏度平方和再开方的值为最小f1(Y);②要求主动轮的质量最小,转变为体积V最小即可,这里使用简化计算来表示齿轮体积。f1(Y)和f2(Y)两者表达式分别为:

所以目标函数为:

(2)建立约束条件
R-R0≥0
40≤h≤60
1100≤D0≤1300
900≤D1≤1100
(3)利用MATLAB 优化函数fmincon 实现对有约束非线性多元变量的优化求解,设定R0=0.9999,选取初值Y0=[1200,1000,50]T,此时F有最小值为 1.9007e+07(优化前为 2.8274e+07)数值明显减小,部分Matlab 代码如下:

采用同样的方法,对极限强度值分别为120MPa、150MPa、160MPa 的材料进行稳健优化设计,得到优化后的尺寸,和目标函数值等信息,如表2 所示。
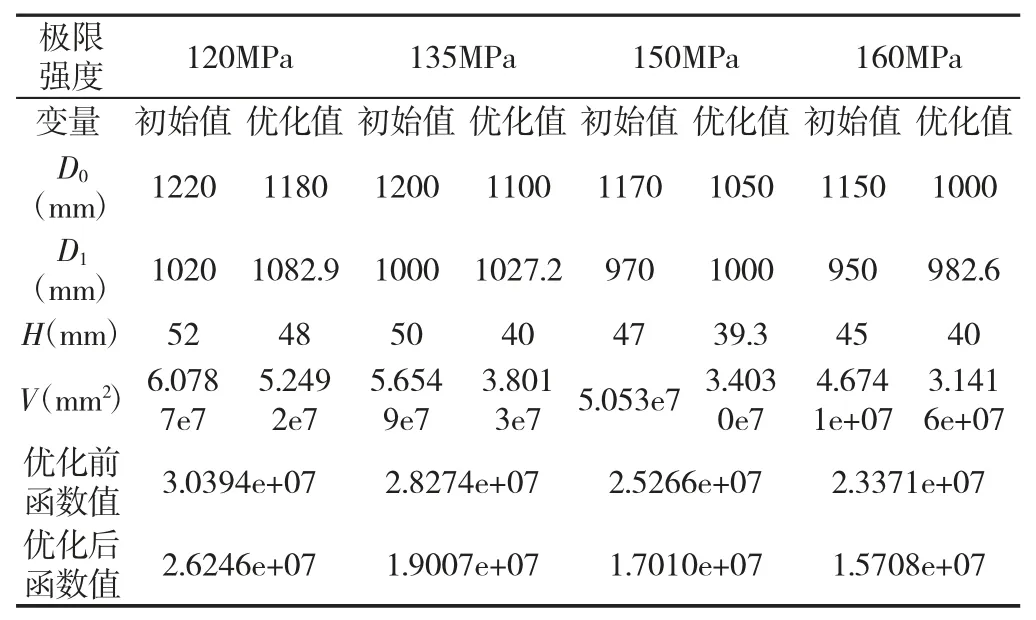
表2 优化前后各变量和函数值数据Tab.2 Before and After Optimization of Variables and Function Value Data
优化前后结构的体积和目标函数值对比图,如图2 所示。从表2 优化前后的结果对比中可以很容易的看出,在保证可靠度为0.9999 的基础上,各设计尺寸都得到了优化,使零件结构的体积减少了(10~30)%,实现了结构的轻量化设计;另外,目标函数中去除体积的减小因素,其余的为灵敏度的减小所致,这使得结构的稳健性得到改善。
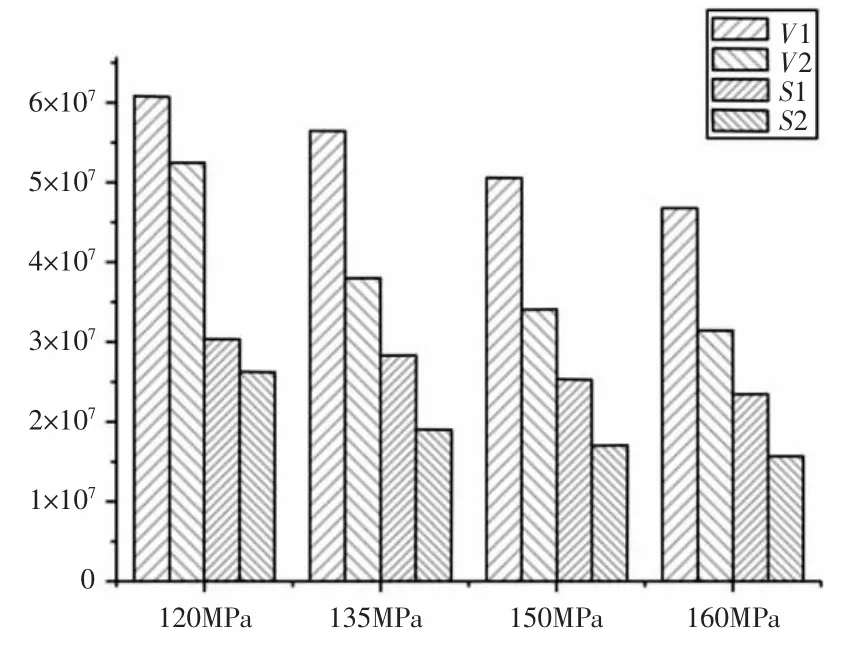
图2 优化前后结构的体积和目标函数值对比Fig.2 Optimization of the Structure Before and After the Volume and Objective Function Value Comparison
在零件用材方面往往是根据经验惯例,选择试用新材料、新结构的往往不多,对于本研究的履带式主动轮结构,实际中通常采用的是135MPa 的材料,如果采用强度更高的150MPa 或160MPa 的新型材料时,零件的结构可以实现更大的轻量化,且可靠性和稳健性也得到了增强。另外,从经济性角度对材料的选择提供参考,利用(优化后体积*材料单价=材料总价)这一方法,对选择不同材料的经济成本进行预算。
5 结论
(1)提出了一种结合可靠性分析和稳健优化设计的综合选材方法,将预选材料的强度作为选材设计变量,以稳健优化设计为选材原则,实现了结构的轻量化和稳健性的提升。(2)利用MATLAB 优化工具箱提供的fmincon 函数对建立的非线性多元变量可靠性稳健优化模型进行求解,得到不同强度设计值的优化数据,结果显示在保证可靠度为0.9999 的基础上,零件结构的体积得到了明显的减少,且结构的稳健性也得到改善。
