变样本容量比例控制图设计及应用

张 莹，周思阳，张 弓

（1.武汉理工大学 物流工程学院，湖北 武汉 430063；2.港口物流技术与装备教育部工程研究中心，湖北 武汉 430063）

0 引言

控制图作为统计过程控制（Statistical Process Control,SPC）的重要工具之一，被广泛应用于监控过程中关键质量特性的波动。目前，如何使用控制图监控两个正态变量之间的比例这一问题受到广泛关注。这是因为在一些实际生产过程中，监控两个变量之间的比例变化比单独监控每个变量的变化更为重要。例如，在煤炭港口的生产过程中，配煤是将各种煤质指标不同的煤按一定的比例配成混合煤，以满足各类客户需求，降低成本，稳定煤质，减少污染物的排放，获得较好的经济、社会和环境效益。其中各种煤炭的比例是一种关键质量特性，在配煤过程中如何监控各种煤炭的比例，确保混合煤的配比稳定是煤炭生产过程中重要的一环。

在使用控制图对变量间比例进行监控的研究中，Celano，等[1]首先针对样本容量n=1 的情况设计了用于监控二元正态变量间比例关系的Shewhart-RZ控制图，并对其统计特性进行了讨论。之后Celano和Castagliola[2]将这项研究扩展到样本容量n ＞1 的情形，并通过一个食品行业的例子说明了Shewhart-RZ 控制图的有效性。为了改善Shewhart-RZ 控制图不能有效检测比例中小偏移的缺陷，Tran，等[3-4]提出了EWMA-RZ控制图和CUSUM-RZ控制图。此后学者们采用不同的策略对比例控制图进行优化，以进一步提高比例控制图的性能。Celano，等[5]将Shewhart-RZ控制图与合格品链长控制图结合，提出了Synthetic-RZ控制图；Nguyen，等[6]开发了Synthetic-RZ控制图的单边版本，计算结果表明单边Synthetic-RZ控制图能有效改善Synthetic-RZ控制图中ARL-biased的问题，并获得更好的统计性能；Tran，等[7]采用运行准则对Shewahrt-RZ控制图进行优化，提出了带有附加运行准则的 Shewhart-RZ 控制图；Nguyen，等[8-10]结合变抽样区间（Variable Sampling Interval，VSI）策略开发了VSIShewhart-RZ控制图、VSI EWMA-RZ控制图和VSI CUSUM-RZ控制图。除了对比例控制图统计性能的优化，Tran，等[11]考虑了需要监控混合物中多种成分间的比例特性的情况，提出了MEWMACoDa控制图；Tran，等[12]，Nguyen和Tran[13]分别研究了测量误差对Shewhart-RZ 控制图和单边Shewhart-RZ控制图性能的影响。

Shewhart型控制图由于易于实现而被广泛采用，同时它们在检测过程均值的大偏移方面提供了良好的性能，但可能需要更长的时间才能检测到中小偏移。解决这一问题的常用方法是使用更高级的控制图，例如带运行规则的控制图、合成控制图、CUSUM控制图或EWMA控制图和使用自适应策略的动态控制图。在动态控制图中可变抽样区间（Variable Sampling Interval，VSI）控制图和可变样本容量VSS控制图是两种常见的类型。王兆军[14]对VSS 控制图的设计理论进行了综述。一些学者研究了VSS型控制图的统计性能，Costa[15]通过将 VSS与 EWMA 控制图、CUSUM 控制图和带有运行规则的Shewhart控制图进行比较，研究了VSS控制图的统计性能。Teoh，等[16]使用运行长度的中位数和运行长度中位数的期望值对VSS控制图进行了优化设计。由于VSS 策略能有效改善Shewhart 型控制图对中小漂移不敏感的缺陷，Castagliola，等[17]提出了VSS t 控制图以改善t控制图对中小偏移的检测性能。Castagliola，等[18]和 Yeong，等[19]提出了 VSS CV 控制图对变量的变异系数进行监控。Annadi，等[20]首先将VSS策略应用于CUSUM 型控制图，提出了VSS CUSUM 控制图，并通过计算说明VSS CUSUM 控制图优于传统的静态CUSUM 控制图，特别当偏移不大时，这种优势更加明显。薛丽[21]将VSS 策略应用于非正态EWMA控制图，并通过计算说明VSS 策略提升了控制图的检测效率。

分析发现，针对比例控制图的研究大多集中于合成比例控制图和VSI 比例控制图，缺乏针对变样本容量策略在比例控制图中应用的研究。针对这一问题，本文提出一种单边变样本容量比例（VSS Shewhart-RZ）控制图来监控两正态变量间的比例特性，比较其与单边Shewhart-RZ 控制图的性能，发现VSS Shewhart-RZ 控制图的性能明显优于Shewhart-RZ 控制图。最后针对港口配煤问题，将其运用于皮带机配煤系统中，对煤炭比例进行监控，以提高配煤质量。

1 单边Shewhart-RZ控制图

W为二元正态随机向量，W=(X,Y)T～N(μW,ΣW)，其均值向量为：

协方差矩阵为：

其中ρ为变量X,Y的相关系数，X,Y的变异系数可分别表示为表示变量X,Y标准差之比。记变量X,Y之比为Z，在文献[2]中Celano和Castaliola给出了变量Z的累积分布函数(c.d.f)、概率密度函数(p.d.f)及逆分布函数(i.d.f)的近似表达式：

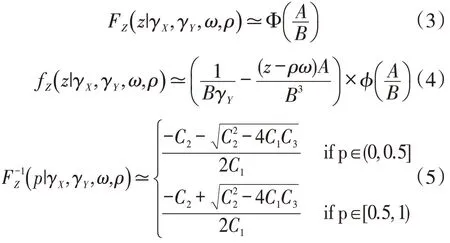
其中 Φ(·)和φ(·)分别表示标准正态分布的c.d.f和p.d.f；A,B,C1,C2,C3为关于z,γX,γY,ω的函数。

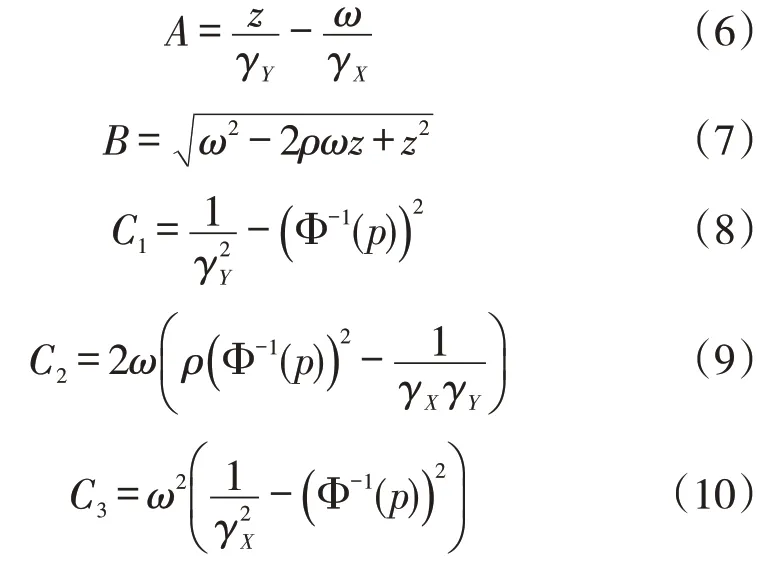
假设在时刻i抽取样本容量为n的样本{Wi,1,Wi,2,…,Wi,n}，样本之间相互独立且服从二元正态分布，Wi,j=(Xi,j,Yi,j)T～N(μW,i,ΣW,i) ，i=1,2,…，1 ≤j≤n，其均值向量为：

协方差矩阵为：

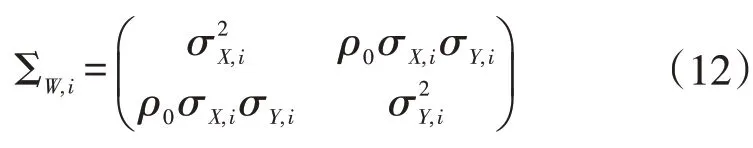
与Celano 和Catagliola[2]一致，本文假设：（1）对于变量X,Y存在σX,i=γX×μX,i，σY,i=γY×μY,i的线性关系，其中变量X,Y的变异系数γX,γY为已知常数；（2）当过程处于受控状态时，变量X,Y的比例为已知常数当过程失控时比例发生偏移，z1=τz0，其中τ表示偏移的大小和方向，τ∈(0,1)时发生向下的偏移，τ ＞1时发生向上的偏移。

为了对比例变量Z进行监控，构造统计量：

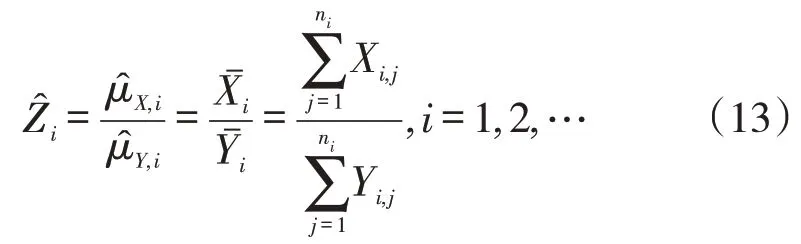
的累积分布函数及其逆函数可由式（3）和式（5）推导得到：

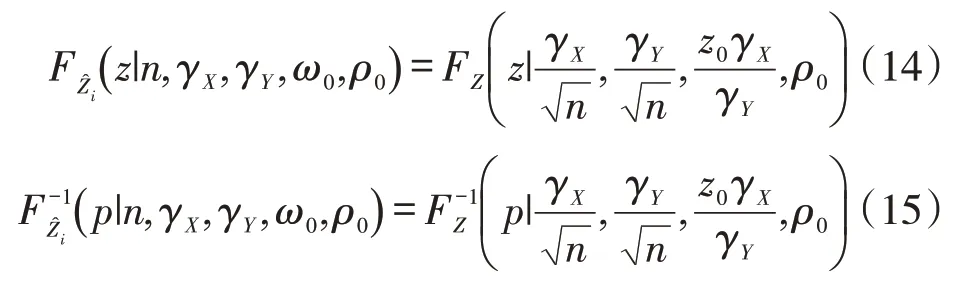
单边Shewhart-RZ 控制图包括检测比例向上偏移的上单边Shewhart-RZ 控制图和检测向下偏移的下单边Shewhart-RZ控制图。对于上单边控制图，仅有上控制限：

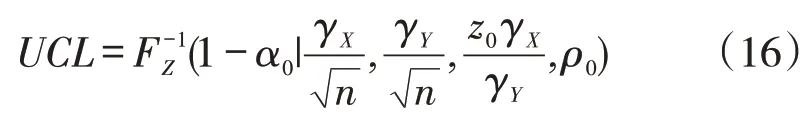
对于下单边控制图仅有下控制限：

其中α0为单边Shewhart-RZ 控制图的虚假报警概率。当统计量大于上单边控制图的上控制限UCL或小于下单边控制图的下控制限LCL时，控制图发出过程失控的警报。

2 单边VSS Shewhart-RZ控制图

2.1 单边VSS Shewhart-RZ 控制图的实施流程

本文在单边比例控制图研究的基础上，增加了动态调整样本容量的自适应策略，提出两个单边变样本容量比例控制图。变样本容量控制策略是指在过程监控中可以根据抽样样本信息动态调整控制图抽样样本容量，而非采用固定的样本容量。在本文中样本容量有两种可能的取值，即小样本容量nS和大样本容量nL，nS ＜nL。通过引入警戒限将控制图分为三个区域：安全区、警戒区和失控区，由式（16）和式（17）可知控制图的上下限受样本容量n的影响，因此当样本容量n取nS或者nL时，会有不同的控制限和警戒限。

检测向上偏移的上单边VSS Shewhart-RZ 控制图在时刻i的控制限可设为UCLi=z0×KU,p，KU,p为上单边控制图的控制限系数，警戒限为UWLi=z0×WU,p，WU,p为上单边控制图的警戒限系数；同理检测向下偏移的下单边VSS Shewhart-RZ控制图的控制限为LCLi=z0×KD,p，警戒限为LWLi=z0×WD,p，KD,p，WD,p分别为下单边控制图的控制限系数和警戒限系数。其中，当n(i)=nS时，p=S；当n(i)=nL时 ，p=L；对 于 上 单 边 VSS Shewhart-RZ 控制图，不同样本容量下的控制限和警戒限系数满足KU,S ＞WU,S，KU,L ＞WU,L；对于下单边VSS Shewhart-RZ 控制图，不同样本容量下的控制限和警戒限系数满足WU,S ＞KU,S，WU,L ＞KU,L。

上单边VSS Shewhart-RZ控制图的运行过程为：

下单边VSS Shewhart-RZ 控制图的运行过程与上单边类似，这里不再详细描述。

2.2 VSS Shewhart-RZ控制图的性能指标

在控制图的设计研究中，通常使用平均运行长度ARL来评价控制图的性能，即从过程开始运行到异常信号产生时所经过的平均样本数。记过程处于受控状态下的平均运行长度为ARL0，失控状态下的平均运行长度为ARL1。当过程处于受控状态时，ARL0越大越好，此时控制图虚发警报的概率降低，可避免多余的停机检查；当过程处于失控状态时，ARL1越小越好，此时控制图漏发警报的概率降低，可以快速检测到异常因素的产生。当样本容量可变时，平均样本容量（Average Sample Size，ASS）也是一种评价指标，ASS=E(n(i))。记过程处于受控状态下的平均样本容量为ASS0，失控状态下的平均样本容量为ASS1。VSS型控制图与静态控制图进行比较时，使受控状态下的ARL0和ASS0保持一致，比较失控状态下的ARL1和ASS1，更小的ARL1或ASS1代表拥有更好的性能。

采用马尔可夫链推导单边VSS Shewhart-RZ 控制图的性能指标，将单边VSS Shewhart-RZ控制图建模为一个含有三种状态的马尔可夫链，其中前两种状态分别对应小样本容量和大样本容量，第三种为吸收态，对应过程失控的情形。该马尔可夫链的转移概率矩阵P为：

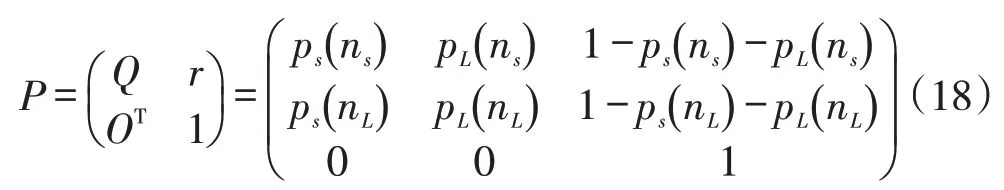
其中I 为2×2 的单位矩阵，q 为初始概率向量。当设定第一组样本的样本容量n(1)=nS时，q=(1,0)T；当设定第一组样本的样本容量n(1)=nL时，q=(0,1)T。本文假设初始状态较为平稳处于安全区域内，设置第一组样本容量为nS，q=(1,0)T。

ASS 的计算需要先将转移矩阵P 转换成P*，当n(1)=nS时：

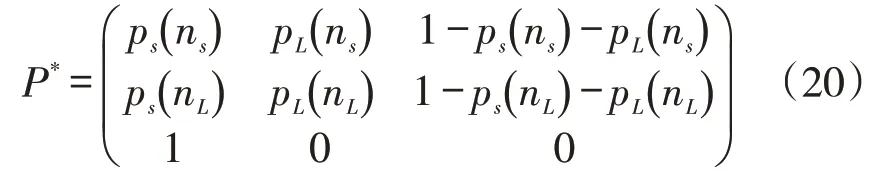
与矩阵P不同，P*没有吸收态，当马尔可夫链到达第三种状态即失控状态时，立刻重启恢复至第一状态。由P*定义的马尔可夫链有稳态概率向量π=(πs,πl,πOOC)T，可由式（21）求得：

其 中 稳 态 概 率 (πs,πl,πOOC) 与 样 本 容 量(nS,nL,n(1))相关。当n(1)=nS时，矩阵R可由矩阵P*先转置，对角线元素减1，并将第一行的元素替换为1，得到：

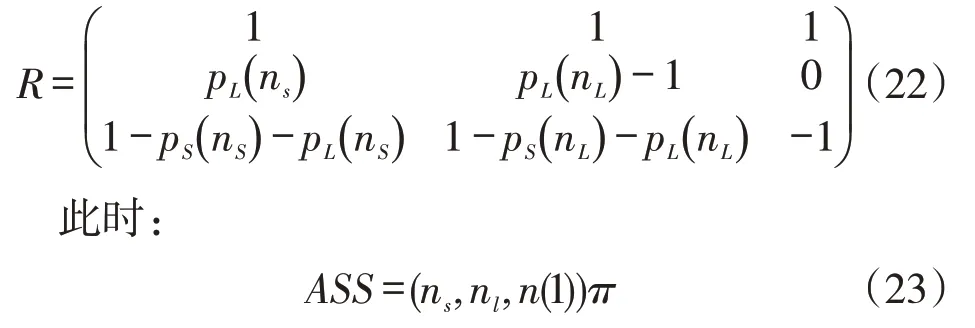
2.3 VSS Shewhart-RZ控制图的设计

本文首先保证过程处于受控状态的统计性能，即保证ARL0和ASS0大小，进而使得过程处于失控状态的平均运行长度最小，即最小化ARL1。此时，VSS Shewhart-RZ 控制图的设计问题转化为带有约束的非线性函数最优化问题。

上单边控制图的优化模型如下：

下单边控制图的优化模型为：

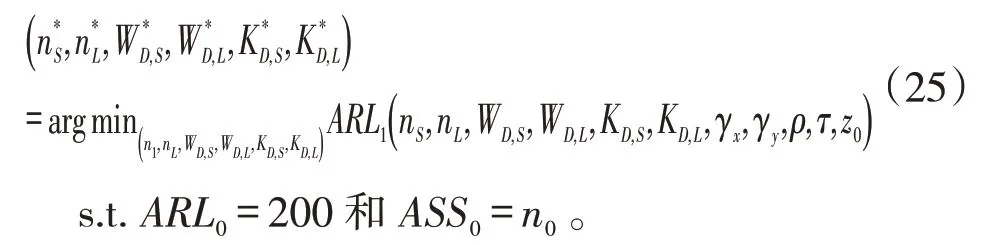
其中ARL0的取值由实际过程中允许的最大虚发警报概率确定，本文为了方便比较，与文献[2-11]中的ARL0的取值保持一致，ARL0=200。n0的取值为实际过程中受控状态下样本容量的希望值，为方便比较，本文取n0={5,15}。同时在实际应用中样本容量的最大值一般会有限制，与文献[17-18]类似，本文设置样本容量可取的最大值为31，则nS,nL需要满足1 ≤nS ＜n0＜nL≤ 31的约束。

（1）设置γx,γy,ρ,τ,z0,n0等参数的取值；

（2）令nS=1；

（3）令nL=n0+1；

（4）在当前参数下，采用Matlab 软件优化工具箱中的fmincon 函数对当前的非线性规划模型进行求解，得到 (WU,S,WU,L,KU,S,KU,L)；

（5）根据当前(nS,nL,WU,S,WU,L,KU,S,KU,L)的取值计算ARL1指标；

（6）保持nS不变，令nL=nL+1；

（7）重复第2步至第4步直至nL=31；

（8）令nS=nS+1；

（9）重复第3步至第8步直至nS=n0-1；

（10）从所有的决策变量组合中选取使ARL1最小的参数。

3 数值分析与比较

本文将研究不同场景下单边VSS Shewhart-RZ控制图的统计性能，并与固定样本容量（Fixed Sample Size，FSS）的单边Shewhart-RZ控制图的统计性能进行比较。为方便分析与比较，本文只研究由比例偏移引起的过程失控，假设在生产过程中两个变量间的相关系数保持不变。本文考虑的一些场景参数如下：

γX∈{0.01,0.2},γX∈{0.01,0.2}，分别对应变量X、Y离散程度较小和较大的情况；

ρ∈{0.0,±0.4,±0.8}，代表变量X、Y 间不同程度的相关性；

n0∈{5,15}，对应使用小样本容量和大样本容量的情形；

τ∈{0.9,0.95,0.98,0.99} 为 向 下 的 比 例 偏 移 ；τ∈{1.01,1.02,1.05,1.1}为向上的比例偏移。

给定参数γX,γY,ρ0,n0,τ的值，可以通过式（24）求得上单边控制图的最优参数通过式（25）求得下单边控制图的最优参数失控状态下的ARL1指标可基于求得的最优参数计算得到，表1和表2展示了过程发生不同大小偏移时单边VSS Shewhart-RZ 控制图和单边FSS Shewhart-RZ控制图的ARL1值。

从表1和表2中可以得出以下结论：

（1）VSS 策略显著提高了单边FSS Shewhart-RZ控制图的统计性能，特别是当偏移较小或变量X,Y的 离 散 程 度 较 大 时 。 如 当γX=0.01,γY=0.01,ρ=-0.8,n0=5,τ=1.01 时，单边 FSS Shewhart-RZ 控制图的ARL1=12.5，而单边VSS Shewhart-RZ控制图的ARL1=4.1，统计性能提升了67.2%。当γX=0.2,γY=0.2,ρ=-0.8,n0=5,τ=0.9 时，单边 FSS Shewhart-RZ控制图的ARL1=42.1，而单边VSS Shewhart-RZ 控制图的ARL1=10.4，统计性能提升了75.2%。

（2）变量X,Y的离散程度 (γX,γY) 的取值对VSS Shewhart-RZ 控制图性能的影响较大，(ρ,n0,τ)等参数保持不变时，(γX,γY)越小越能快速检测到比例 的 偏 移 。 如 当ρ=-0.8,n0=5,τ=1.05 并 且γX=0.01，γY=0.01 时，VSS Shewhart-RZ 控制图的ARL1=1，当γX=0.2，γY=0.2 时，ARL1=32.7。

（3）变量X,Y间的相关系数ρ0对VSS Shewhart-RZ控制图的性能有所影响，(γX,γY,n0,τ)等参数保持不变时，ρ的取值越大即变量间的正相关性越强，控制图的性能越好。如γX=0.01,γY=0.01,n0=5,τ=1.01且ρ=-0.8 时，VSS Shewhart-RZ 控制图的ARL1=4.1；当ρ=0.8 时，ARL1=1.3。

（4）受控状态下的平均样本容量n0的取值也会对VSS Shewhart-RZ控制图的性能有所影响，n0越大控 制 图 的 性 能 越 好 。 如 当γX=0.01,γY=0.01,ρ=-0.8,τ=1.01 且n0=5 时，VSS Shewhart-RZ 控制图的ARL1=4.1；而当n0=15 时，ARL1=2.3。

4 煤炭配比仿真实验

本文通过仿真实验说明单边VSS Shewhart-RZ比例控制图在煤炭港口配煤过程中对煤炭比例进行监控的应用。在散货码头物流装备实验室中对配煤比例监测环节做仿真实验，假设需要监测的两类煤炭（神混一，平混六）的目标混合比例为1：1（z0=1），在生产过程中两类煤炭各由一条皮带机运输，最后在筒仓内混合。为监控两类煤炭的比例，对一定时间内两条皮带的流量进行抽样检测，将两类物料的质量用变量(X,Y)表示。抽样检验时分别截取两个皮带机上30s内运输的物料进行称重，记录两类物料的质量作为一个样本。在进行监控前需要通过多次抽样对过程参数进行估计，并确定过程处于稳定状态，由此得到γX≈0.05,γY≈0.05,ρ=0 。

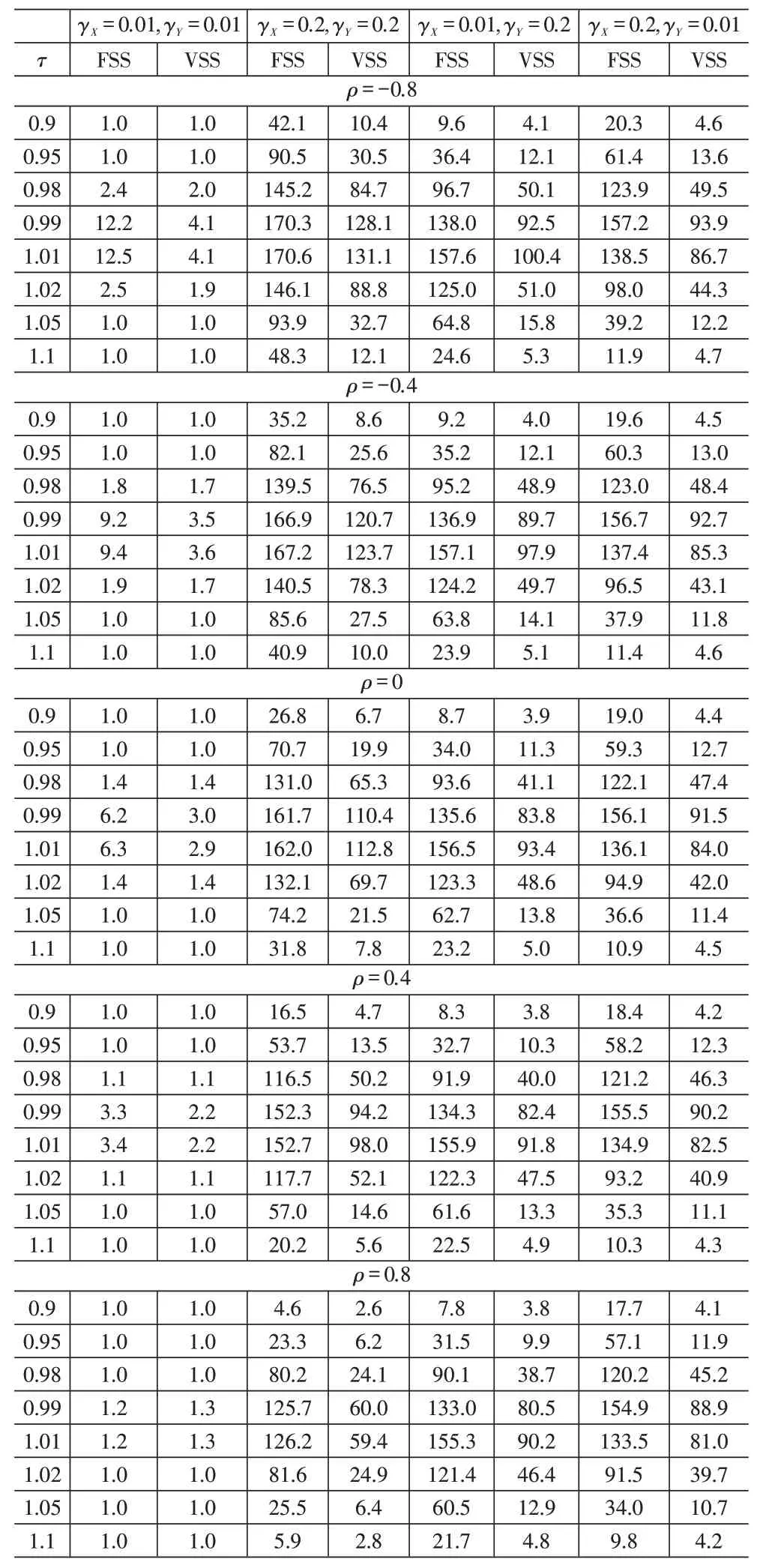
表1 n0=5 时，单边VSS Shewhart-RZ和单边FSS Shewhart-RZ控制图的ARL1

由第3节分析，以n0=5 为例，针对生产过程中两种煤炭的比例z0可能偏移至z1=1.1 的情况，对上单边VSS Shewhart-RZ控制图进行优化设计，计算得到决策变量的取值为nS=4,nL=12,小样本时的控制限和警戒限分别为KU,S=1.094 6,WU,S=1.038 0，大样本时 的 控 制 限 和 警 戒 限 分 别 为KU,L=1.059 0,WU,L=1.040 5，此时控制图失控状态下的平均运行长度为ARL1=1.48。

表2 n0=15 时，单边VSSShewhart-RZ和单边FSSShewhart-RZ控制图的ARL1

实验中共进行了15次抽样，在前10次抽样时模拟受控状态下的生产过程，让设备正常运转；在第10次抽样后让其中一个皮带每次运行33s 以模拟生产失控导致物料比例偏移至z1=1.1 的情况。根据采集到的数据可绘制上单边VSS Shewhart-RZ 控制图如图1所示，前10次抽样结果皆位于控制限之下，表示过程处于受控状态。当第10次抽样样本容量发生变化后，控制图通过第12-15样本点超出控制限及时发出警报，表明过程失控，需要对生产过程进行检查以恢复正常生产。

图1 上单边VSS Shewhart-RZ控制图

5 结语

本文针对实际生产中需要对二元正态变量间的比例特性进行监控的问题，提出采用两个单边VSS Shewhart-RZ 控制图来监控过程中的比例变量，采用马尔可夫链方法推导出VSS Shewhart-RZ 控制图的平均运行长度和平均样本容量指标，通过优化失控状态下的平均运行长度指标研究了单边VSS Shewhart-RZ控制图的统计性能。实验结果表明了单边VSS Shewhart-RZ 控制图相对于Shewhart-RZ控制图的优越性，尤其当偏移较小或变量X,Y的变异系数较大时，VSS Shewhart-RZ 控制图的性能优势更加显著。港口配煤生产过程中，采用单边VSS Shewhart-RZ 控制图来监控煤炭的混合比例，可以迅速对比例偏移做出反应，有效减少不合格混合煤的产生，提高生产效率。本文仅研究了VSS 策略在Shewhart 比例控制图中的应用，其在EWMA 和CUSUM比例控制图中的应用还需要进一步研究。