GOCE卫星重力梯度观测值的时变重力场变化改正及影响分析

陈鑑华，张兴福，沈云中，陈秋杰，李伟超

1. 广东工业大学测绘工程系，广东 广州 510006； 2. 同济大学测绘与地理信息学院，上海 200092； 3. 波恩大学大地测量与地理信息学院，波恩 53121

2009年，欧空局(European Space Agency，ESA)发射了GOCE(gravity field and steady-state ocean circulation explorer)卫星，其主要科学目标是确定约100 km分辨率、1～2 cm精度的大地水准面，可为固体地球物理学、海洋学、大地测量学和冰川学等科学研究提供高精度的中高阶静态地球重力场模型[1]。GOCE卫星在任务期间共获取了约42个月的有效重力梯度观测值，由于重力梯度观测值包含了时变重力场变化信号，在高阶静态重力场反演中需考虑时变重力场变化改正的影响。ESA在Level 2级别的GOCE卫星重力梯度数据中给出了ESA计算的时变重力场变化改正值[2]，目前国内外绝大多数科研机构均直接利用GOCE卫星Level 2重力梯度数据进行重力场反演[3-5]，但时变重力场变化改正是实现由GOCE卫星Level 1b级别数据到Level 2级别数据转换的重要过程，也是完整GOCE卫星数据处理过程中的一个重要环节，而ESA有关文档中并未给出详细的数据处理过程，自主实现由GOCE卫星Level 1b重力梯度数据直接进行重力场反演具有重要的科学意义，可为我国独立开展相关GOCE类卫星任务的数据处理研究提供重要参考。

GOCE卫星重力梯度观测值的时变重力场变化改正主要包括直接潮汐改正、固体潮汐改正、海洋潮汐改正、极潮改正和非潮汐质量变化改正等[6-7]。鉴于GOCE卫星重力梯度观测值的时变重力场变化改正的重要性，国内外已有学者对重力梯度的时变重力场变化改正展开研究[7-16]，分别从功率谱密度特性[13-15]以及时变重力场变化的高频信号源[9-10]等方面分析了时变重力场变化改正对GOCE卫星重力梯度观测值的影响。但目前暂未见从重力场反演结果层面分析时变重力场变化改正及标准和背景模型更新对高阶静态重力场反演的影响等相关研究成果。基于上述背景，本文采用直接法进行GOCE卫星重力反演，并进行有关分析，首先选用和ESA一致或同类的标准和背景模型计算出时变重力场变化改正值并与ESA结果进行比较，验证本文计算的正确性；然后采用新标准和背景模型对GOCE卫星重力梯度观测值进行时变重力场变化改正，自主实现了由Level 1b重力梯度数据直接进行重力反演；最后通过3种时变重力场变化改正方案分别反演220阶次的重力场模型，从大地水准面阶误差和不同方案模型间全球大地水准面差异等方面来分析时变重力场变化改正对高阶静态重力场反演结果的影响，并利用实测大地水准面模型对结果进行检核。

1 原理与方法

GOCE卫星的主要任务是反演高精度的静态地球重力场，但重力梯度观测值包含了时变重力场变化信号，需要考虑对其进行时变重力场变化改正，主要包括：直接潮汐改正、固体潮汐改正、海洋潮汐改正、极潮改正和非潮汐质量变化改正等，其中，直接潮汐改正先计算引潮位，再将其转换为重力梯度改正值，而固体潮汐改正、海洋潮汐改正、极潮改正、非潮汐质量变化改正是先确定对应的位系数改正数，然后将其转换为重力梯度改正值。

1.1 直接潮汐改正

直接潮汐是由日月及其他天体对卫星的引潮力引起的，对应的引潮力位Vj可表示为[17]

(1)

1.2 固体潮汐改正

固体潮汐引起的重力位系数改正可分为两步计算[18]。

第1步：计算固体潮汐引起的2阶和3阶重力位系数改正，以及2阶对4阶重力位系数的改正，公式为

(2)

(3)

第2步：计算2阶项的日潮、半日潮及长周期潮改正，其中计算日潮改正的公式为

(4)

2阶项的潮汐校正包含48个日潮、两个半日潮以及21个长周期潮(其他具体计算公式可参考文献[18])，f为各潮波分量,Ampf(ip/op)和其他相关参数含义可通过文献[18]获得。

1.3 海洋潮汐改正

由海洋潮汐引起的重力位系数改正数可用式(5)计算[18]

(5)

1.4 极潮改正

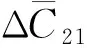
(6)

式中，m1、m2参数含义及其具体计算过程可参考文献[18]。

1.5 非潮汐质量变化改正

非潮汐质量变化改正包括大气与海洋非潮汐质量变化改正、陆地水质量变化改正和冰雪质量变化改正等地表质量季节性变化的改正。

1.5.1 大气与海洋非潮汐质量变化改正

ESA提供的大气质量变化改正采用ECMWF(European Centre for Medium-range Weather Forecast)模型计算，其海洋非潮汐质量变化改正采用OMCT(ocean model for circulation and tides)模型数据计算。由于GFZ研发的AOD1B(Atmosphere and Ocean De-aliasing level-1B)模型给出了大气和海洋非潮汐变化模型，因此，本文直接采用AOD1B模型中提供的有关重力位系数的改正数进行计算。

1.5.2 地表质量季节性变化改正

地表质量季节性变化改正主要为陆地水质量变化改正和冰雪质量变化改正等，而GRACE月时变重力场模型已扣除了各种潮汐及大气和海洋非潮汐质量变化影响，剩余的时变重力场变化信号主要来自地表质量季节性变化信号，因此，可以采用GRACE月时变重力场模型计算地表质量季节性变化影响的改正值[6,10]。

2 计算结果验证与更新比较

为验证本文时变重力场变化改正的正确性，并分析标准和背景模型更新前后时变重力场变化改正结果的差异，本文选择了2010年6月1日的GOCE卫星实测数据，分别计算出各项潮汐改正值以及非潮汐质量变化改正值，并进行有关比较与分析，所采用的标准和背景模型信息见表1，其中“ESA”表示ESA标准，“Tongji”表示本文采用的新标准。后文计算结果中，“ESA”表示ESA发布结果；“Tongji”表示本文按照新标准计算结果；“Tongji(ESA)”表示本文按照ESA标准计算结果，其中计算大气与海洋非潮汐质量变化改正时，采用了AOD1B RL05模型来代替ECMWF和OMCT模型，其他与ESA标准一致。

表1 标准和背景模型信息

2.1 时变重力场变化改正结果验证

ESA和Tongji(ESA)比较结果见图1—图5，两者差值标准差的统计结果见表2。综合图1—图4以及表2可得，当采用的标准和背景模型与ESA一致时，本文的计算结果与ESA的结果是吻合的；本文计算值与ESA结果差值的标准差比对应潮汐改正值的最大量级低1～3个量级，说明本文的潮汐改正结果是正确的。图5结果显示，本文非潮汐质量变化计算值与ESA发布结果在数值上稍有差异，产生差异的主要原因是所使用的背景模型不完全一致(本文计算大气与海洋非潮汐质量变化采用的背景模型为AOD1B RL05模型)，但两者在趋势和量级上具有较好的一致性，说明本文非潮汐质量变化改正值计算结果应该是可靠的。综合看，本文时变重力场变化改正的结果是正确的，在所有改正项中，海潮改正的量级最大，其次为非潮汐质量变化改正，极潮改正的量级最小。

图1 直接潮汐改正值与ESA结果比较Fig.1 Comparisons between direct tide corrections and ESA results

图2 固体潮汐改正值与ESA结果比较Fig.2 Comparisons between solid tide corrections and ESA results

2.2 ESA标准和背景模型更新比较

由于ESA计算重力梯度观测值的时变重力场变化改正所采用的标准和背景模型较老，理论上，新标准和背景模型能更好地模型化时变重力场变化信号，因此本节探讨标准和背景模型更新前后时变重力场变化改正值的差异(新标准和背景模型采用表1中“Tongji”项)，计算结果比较见图6。由图6可知，更新的标准和背景模型会影响时变重力场变化改正的结果，但更新前后两者的时变重力场变化改正值趋势一致，大小稍有差异但差异不大，总量在同一量级，下文将详细分析标准和背景模型更新前后对高阶静态重力场反演的影响。

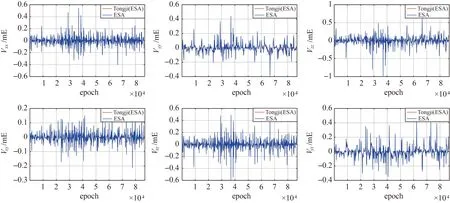
图3 海洋潮汐改正值与ESA结果比较Fig.3 Comparisons between ocean tide corrections and ESA results

图4 极潮改正值与ESA结果比较Fig.4 Comparisons between pole tide corrections and ESA results

表2 Tongji(ESA)与ESA结果的差值标准差

图5 非潮汐改正值与ESA值的比较Fig.5 Comparisons between non-tidal corrections and ESA results

图6 Tongji和ESA的时变重力场变化改正值比较Fig.6 Comparisons of temporal gravity field variations corrections between Tongji and ESA

3 时变重力场变化改正对高阶静态重力场反演的影响分析

本节设计了3种方案来分析时变重力场变化改正对利用GOCE卫星重力梯度数据反演高阶静态重力场的影响，分别为：①无改正方案(Case 1)，不进行任何时变重力场变化改正；②ESA方案(Case 2)，采用ESA发布的时变重力场变化改正值；③Tongji方案(Case 3)，采用新标准和背景模型计算时变重力场变化改正值，3种方案差异仅在于时变重力场变化改正值，其他数据处理方法完全一致。

考虑到低轨道GOCE卫星对重力场信号更敏感，本文采用GOCE卫星2012年10月—2013年4月期间新版的Level 1b重力梯度观测数据[23]，按照上述3种方案进行高阶静态重力场反演。首先选择GIF48模型截断至300阶次作为本次反演的参考模型，利用频带范围为5～100 mHz的IIR带通滤波器对扰动重力梯度值进行带通滤波，采用直接法构建反演220阶次重力场模型的法方程；然后与180阶次的Tongji-Grace02s模型[24]法方程进行融合，反演220阶次的无约束重力场模型。在数据融合过程中单位权中误差取GRACE卫星的轨道精度，GRACE KBR观测值精度取验后统计精度，而重力梯度分量的精度根据滤波之后的扰动重力梯度值进行统计确定。3种方案解算模型和Tongji-Grace02s模型的大地水准面阶误差如图7所示，比对模型为EIGEN-6C4模型。

图7 各方案模型与EIGEN-6C4模型比较大地水准面阶误差Fig.7 Geoid degree error of different models with respect to EIGEN-6C4

图7结果显示，3种方案解算模型的大地水准面阶误差几乎一致，不能明显地分析时变重力场变化改正对静态重力场反演的影响。融合了GOCE卫星重力梯度数据后，模型大地水准面阶误差相对于Tongji-Grace02s模型在72阶次后逐渐有了改善，在108阶次后其改善效果更为明显，说明相比GRACE卫星，GOCE卫星重力梯度数据对中高阶重力位系数的贡献更大，因此在中高阶的位系数精度改善效果会比较明显。为了更清晰地分析时变重力场变化对静态重力场反演的影响，本文计算了全球1°×1°的大地水准面(220阶次)，其比较结果见图8(a)、图8(b)和图8(c)，同时图8(d)给出了100～220阶次不同方案反演模型所对应大地水准面差异的统计结果。

由图8(a)和图8(b)可知，时变重力场变化改正对重力场反演是有影响的，其在局部区域的大地水准面差异的绝对值最大达到1.4 cm，差异主要体现在南北两极、阿根廷东部沿海和欧洲等地区，这些地区也是该时间段时变重力场变化信号较为明显的区域，如果采用的数据观测时间段不同，时变重力场变化影响会有所差异。但由图8(c)可知，采用不同的标准和背景模型同样也会影响高阶静态重力场反演结果，两者在南北两极、亚马孙河口附近和欧洲等区域中稍有差异。由图8(d)可知，从全球大地水准面差异看，在220阶次，时变重力场变化改正对静态重力场反演的整体影响超过1 mm，影响主要体现在中高阶次位系数，低于120阶次的影响很小。综合图8可知：GOCE卫星重力梯度观测值的时变重力场变化改正是需要的，且不同标准和背景模型对静态重力场反演的影响稍有差异。

图8 不同模型间的全球大地水准面比较Fig.8 Comparison of global geoid height between different models

为进一步检核时变重力场变化改正对利用GOCE卫星重力梯度数据反演高阶静态重力场的影响，同时考虑到南北两极可能会受到极区空白的影响，而极区空白对远离两极的区域大地水准面的精度影响较小[25]，因此本文利用收集到的欧洲区域(图8中时变重力场影响较大的区域)约1 cm精度的France水准面模型RAF18(图8(b)中的A区域)和Great Britain水准面模型OSGM15(图8(b)中的B区域)对本文3种反演方案获得的重力场模型进行精度评定，精度统计结果见表3(其中截断阶次后采用EIGEN-6C4模型填充至2160阶次)。

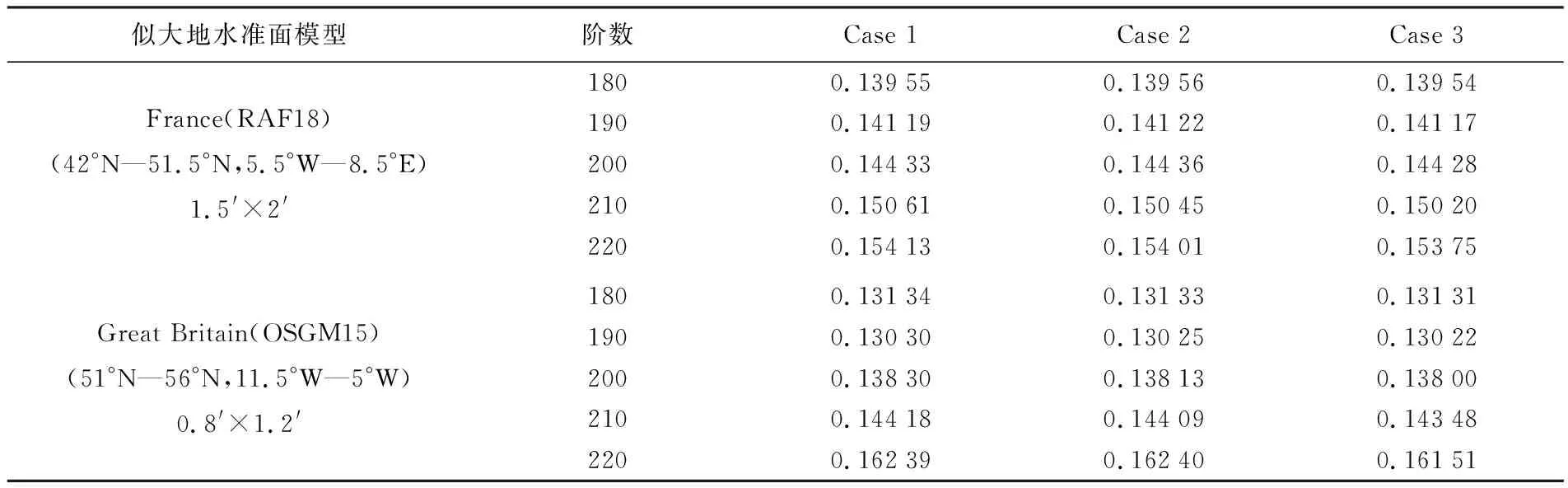
表3 RAF18和OSGM15水准面模型评估模型的精度统计

表3结果表明，虽然不同方案模型间差异不大，但综合看，进行时变重力场变化改正(Case 2和Case 3)方案比无改正方案(Case 1)解算的模型精度稍好，说明重力梯度观测值的时变重力场变化改正是有效的，同时Tongji方案(Case 3)精度稍优于ESA方案(Case 2)，说明背景模型和标准的更新更有利于扣除时变重力场变化信号，从而提高高阶静态重力场反演的精度。

4 结束语

本文研究了GOCE卫星重力梯度观测值的时变重力场变化改正方法，更新了ESA标准和背景模型，并从重力场反演角度分析了时变重力场变化改正对高阶静态重力场反演的影响，实现了从GOCE卫星Level 1b重力梯度数据直接进行重力场反演，主要结论如下。

(1) 在时变重力场变化改正中，海洋潮汐改正值的量级最大，其次为非潮汐质量变化改正，极潮改正值的量级最小。利用3种时变重力场变化改正方案进行高阶静态重力场模型反演，并进行分析与比较，结果表明：从全球大地水准面比较可看出时变重力场变化改正对重力场反演结果是有影响的，其影响在局部区域的大地水准面差异绝对值最大达到1.4 cm；在全球范围内对重力场反演的整体影响超过1 mm，因此利用GOCE卫星重力梯度观测值反演高阶静态重力场时需要扣除时变重力场变化的影响。

(2) 利用France水准面模型RAF18和Great Britain水准面模型OSGM15检核3种方案模型的精度，结果表明进行时变重力场变化改正方案比无改正方案解算的模型精度稍好，且更新后的标准和背景模型更有利于扣除时变重力场变化的影响。