单级倒立摆系统的仿真分析

李艳杰 佟福奇

沈阳理工大学 机械工程学院 沈阳 110159

1 分析背景

倒立摆系统是一个非线性、强耦合、多变量自然不稳定系统,需要采用有效的控制策略。基于倒立摆系统,可以检验控制理论与方法的合理性、有效性。军工、航天及一般工业中的很多问题都可以简化为倒立摆系统,如人型机器人行走过程中的平衡控制问题、航天飞行器飞行中的姿态控制问题等。

单级倒立摆系统可以简化为小车和摆杆两部分。小车由电机带动,沿直线轨道移动。摆杆与小车铰接,可绕铰接点旋转。单级倒立摆系统的控制目标是通过向小车施加控制力,使小车停留在期望的位置,并且摆杆竖直向上。

自20世纪50年代美国麻省理工学院设计出一级倒立摆实验装置以来,众多学者对单级倒立摆系统的控制与仿真进行了大量研究。杨世勇等[1]对单级倒立摆系统进行了比例积分微分控制研究。李秋菊等[2]针对单级倒立摆系统提出一种基于广义扩展线性化的非线性控制方法,并进行了仿真分析。蒲建波等[3]在Matlab软件中建立单级倒立摆系统的线性化仿真模型,进行多种控制方法的仿真对比。

笔者针对单级倒立摆系统设计了双比例积分微分控制、极点配置控制、线性二次型调节器控制三种控制方案[4-10],在单级倒立摆系统数学模型的基础上,应用Matlab/Simulink软件Simscape子模块建立单级倒立摆系统的物理仿真模型,进行控制方案的对比与分析。

2 单级倒立摆系统数学模型

忽略空气阻力及摆杆与支点之间等各种次要摩擦阻力后,将直线单级倒立摆系统抽象为由小车和匀质刚性摆杆组成的系统,如图1所示。

图1 单级倒立摆系统

对小车和摆杆进行受力分析后,运用牛顿第二定律,得到小车和摆杆在水平、竖直方向共四个力的平衡方程,以及摆杆绕质心的力矩平衡运动方程。消去大小相等的小车和摆杆之间的水平、竖直方向相互作用力后,可以得到单级倒立摆系统的运动方程,为:

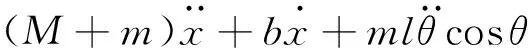
(1)

(2)

式中:M为小车质量;m为摆杆质量;I为摆杆绕质心的转动惯量;l为摆杆质心与转动轴心间的距离;b为小车与导轨之间的黏性摩擦系数;g为重力加速度;θ为摆杆与竖直向下方向之间的夹角;F为施加在小车上的作用力;x为小车水平位移。

可见,单级倒立摆系统具有非线性、强耦合的特点。φ为摆杆与竖直向上方向之间的夹角,为了便于设计控制器,可以在φ为0°时对系统进行线性化处理。

用u代表施加在小车上的作用力F,得到线性化后运动方程为:

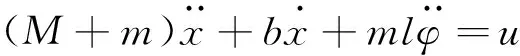
(3)

(4)

(5)

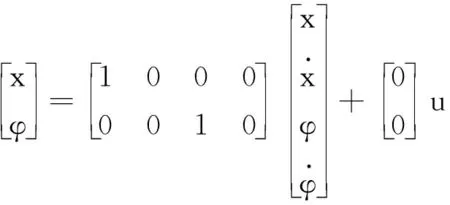
(6)

单级倒立摆系统具体参数如下:M为0.2 kg,m为0.5 kg,I为0.006 kg·m2,l为0.3 m,b为0.1 N/(m·s)。将参数代入式(5),可得状态空间方程中的系统矩阵A为:

输入矩阵B为:

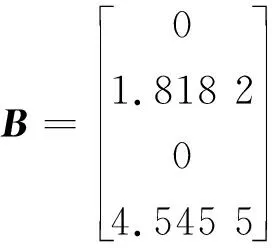
3 单级倒立摆系统物理仿真模型

Simscape是Matlab/Simulink软件中的一个子模块。使用Simscape子模块中的刚体、关节、约束、力元件、传感器等模块,可以建立多体系统物理仿真模型,实现在Matlab/Simulink软件中对控制器和控制对象同时建模,避免多平台联合建模对仿真效率的影响。

建立单级倒立摆系统的物理仿真模型,如图2所示。环境变量包括重力、维度等,一般不需要设置。基于世界坐标、坐标变换1、坐标变换2,小车和摆杆建立空间位置联系。设置移动关节和旋转关节,建立旋转运动。小车在控制力的作用下移动,设置关节传感器以观测小车的位移和速度、摆杆的角位移和角速度等变量。单级倒立摆系统三维模型如图3所示。

向小车施加单位阶跃力,得到响应曲线,如图4所示。由图4可以看出,如果不进行反馈控制,摆杆将产生周期振荡。假设导轨足够长,小车将持续运动,速度越来越快。由此可见,单级倒立摆系统是自然不稳定系统。

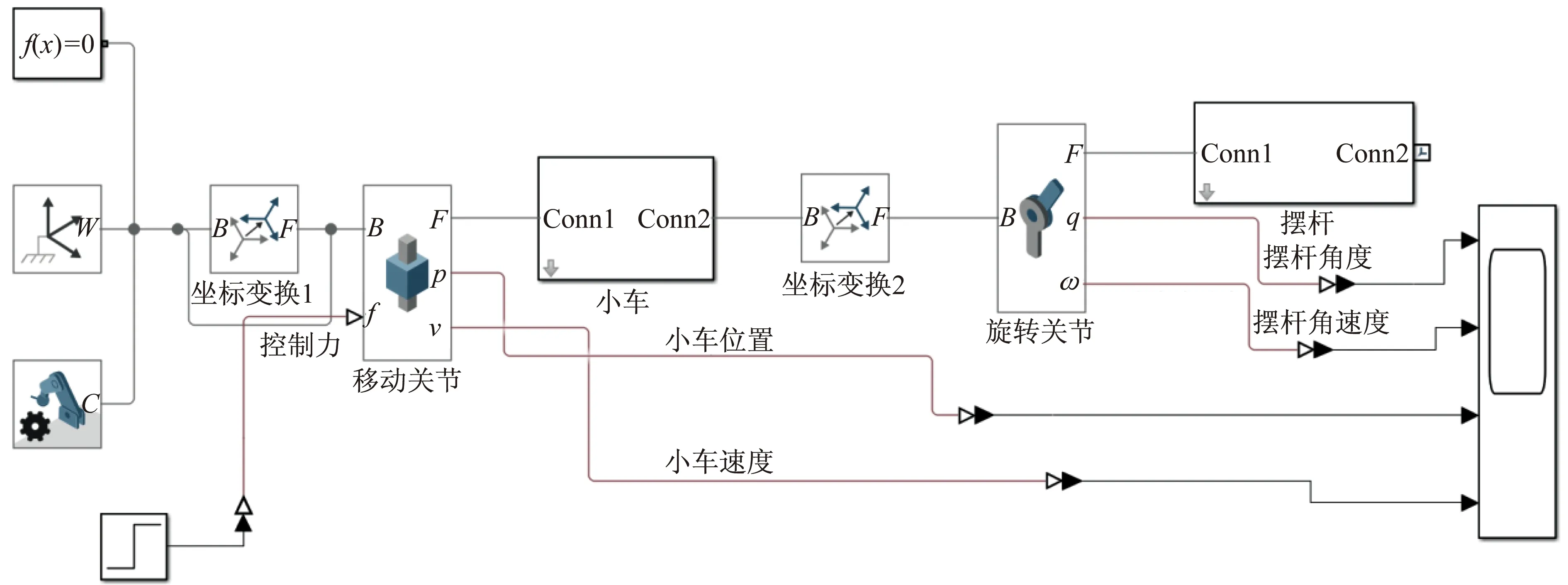
图2 单级倒立摆系统物理仿真模型

图3 单级倒立摆系统三维模型

4 控制方案分析

4.1 双比例积分微分控制

比例积分微分控制具有结构简单、易于调节的特点,不需要精确数学模型,就可以达到较好的控制效果。为了对摆杆和小车都进行控制,可以采用双闭环比例积分微分控制,实现小车在指定位置时摆杆竖直向上的控制目标。由于摆杆和小车之间存在变量耦合,双比例积分微分控制的参数调整过程比较耗时,一般采用经验法进行调整。双比例积分微分控制单级倒立摆系统仿真模型如图5所示。

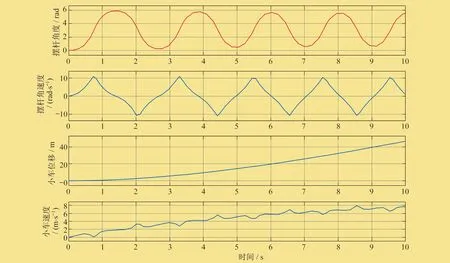
图4 单级倒立摆系统阶跃响应曲线

通过反复试验,小车位置比例、积分、微分参数依次整定为50、50、8,摆杆比例、积分、微分参数依次整定为80、100、8。双比例积分微分控制单级倒立摆系统响应曲线如图6所示,可以看出小车平衡在设定的位置,摆杆维持竖直向上方向。

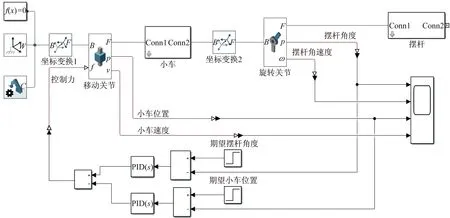
图5 双比例积分微分控制单级倒立摆系统仿真模型

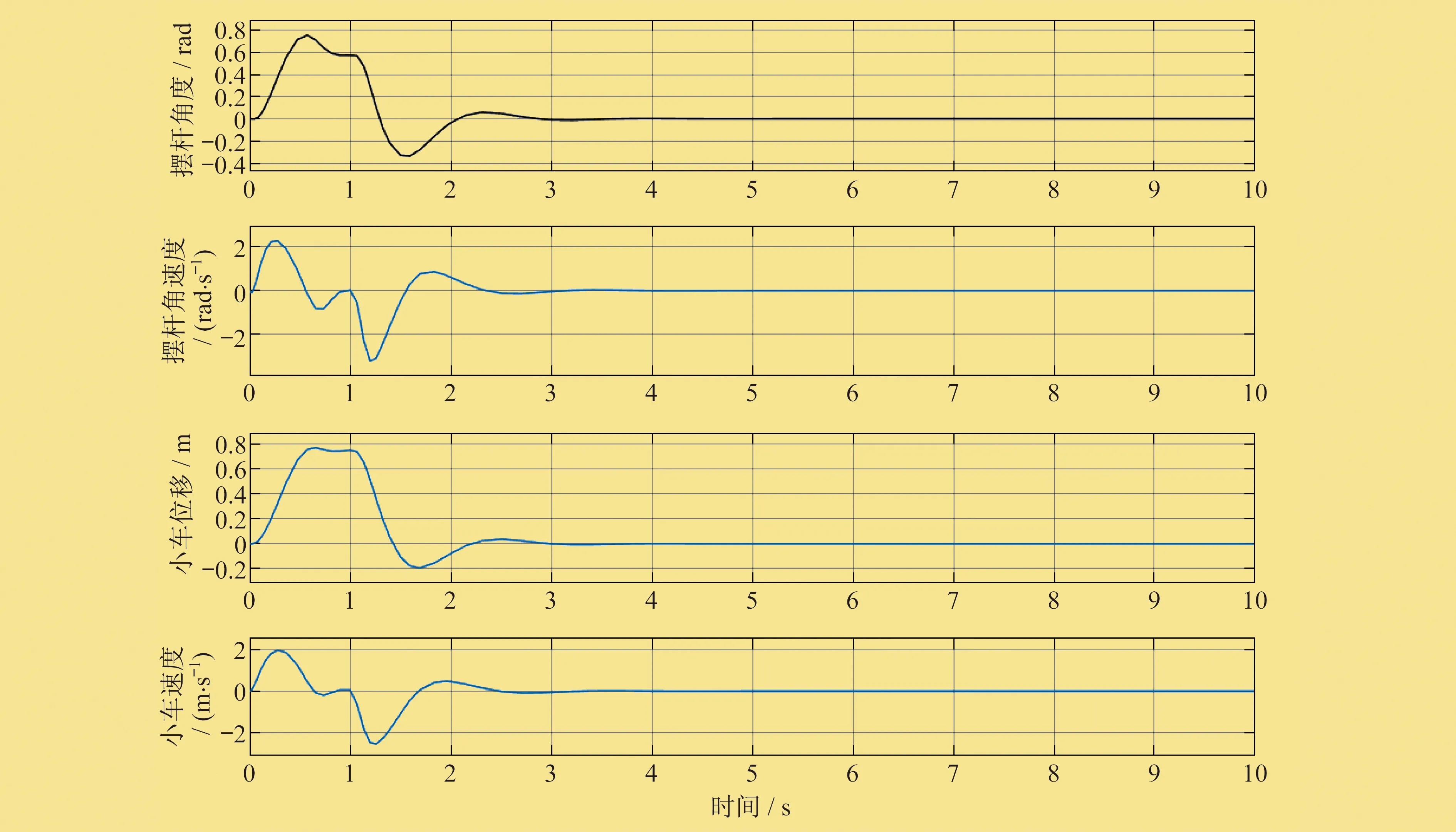
图6 双比例积分微分控制单级倒立摆系统响应曲线

4.2 极点配置控制分析

状态空间极点配置控制可以通过设计状态反馈控制器,将多变量系统的闭环系统极点配置在期望的位置,从而使系统满足性能指标的要求。极点配置控制原理如图7所示。

根据单级倒立摆系统性能指标的要求,设定好期望的闭环极点,利用Matlab软件中的PLACE函数可以方便获得状态反馈增益矩阵[k1k2k3k4],此时系统的控制律为:

(7)

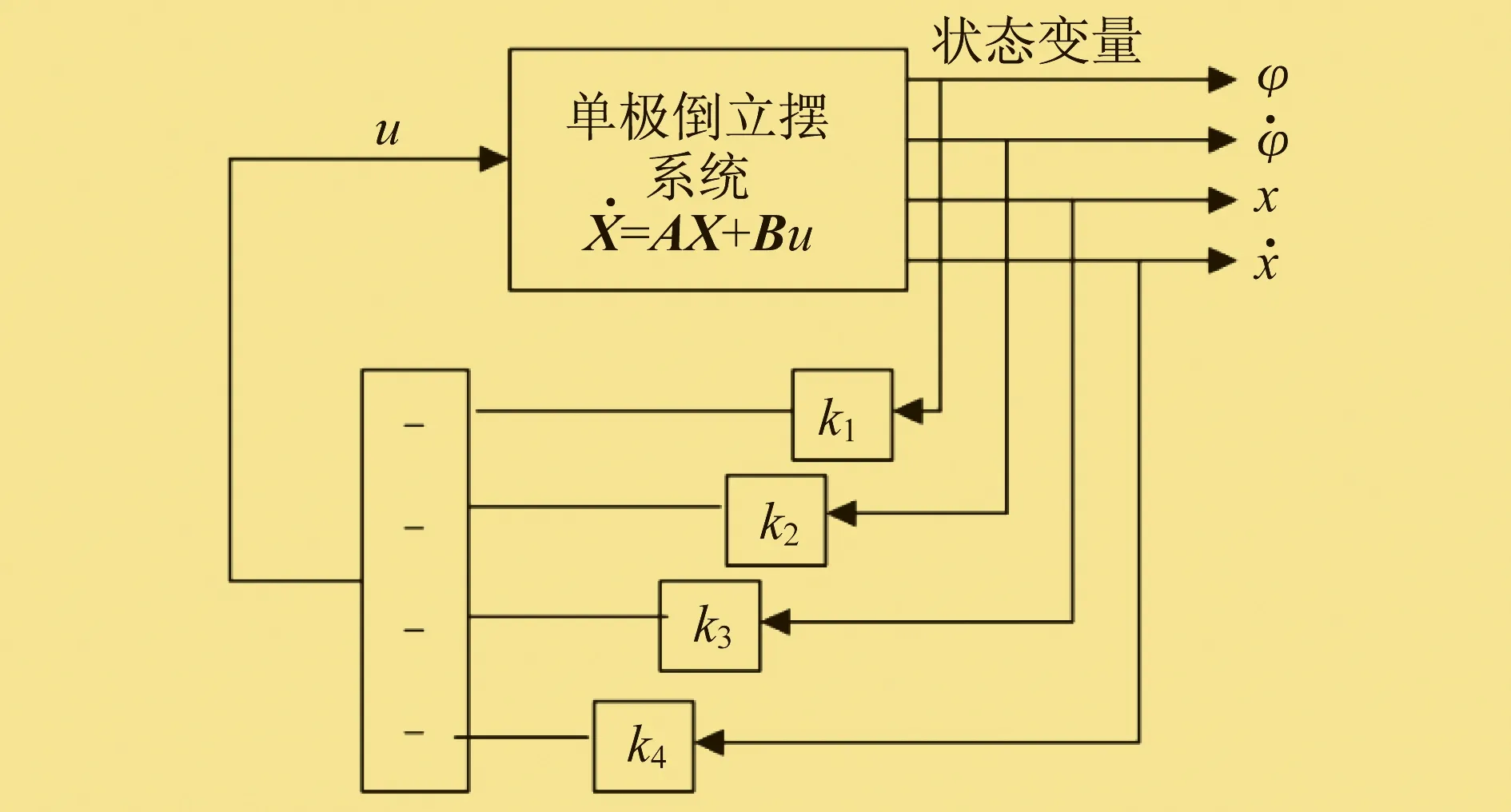
图7 极点配置控制原理

利用Matlab软件中的PLACE函数,可以直接获得极点配置控制的增益,语句格式为K=PLACE(A,B,P),其中,P为配置极点,K为反馈增益矩阵。取期望配置极点P为(-10,-10,-0.6+1.171j),运行PLACE函数,得到k1为105.537 7,k2为17.948 2,k3为-77.717 7,k4为-27.920 7。

极点配置控制单级倒立摆系统仿真模型如图8所示,在模型中引入对摆杆的阶跃干扰信号,幅值为0.5,作用时长为0～1 s。极点配置控制单级倒立摆系统响应曲线如图9所示。

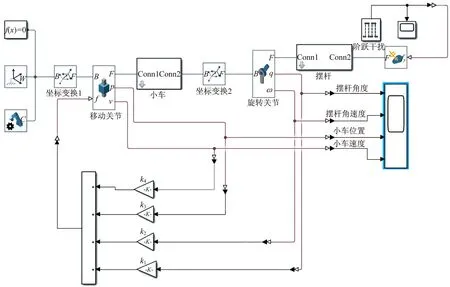
图8 极点配置控制单级倒立摆系统仿真模型

仿真结果表明,单级倒立摆系统在扰动信号消失大约3 s后,以较小的超调量稳定在平衡位置,控制方案有效。

4.3 线性二次型调节器控制分析

线性二次型调节器控制是一种应用广泛的最优控制方法,其控制原理如图10所示。

系统二次型调节器控制性能指标函数J为:

(8)

Q、R为加权矩阵变量,用于平衡输入向量和状态向量之间的权重。Q为半正定矩阵,R为正定矩阵。理论上Q的元素可在0到无穷大之间取值。Q的元素越大,系统的调整时间越短,响应越快。但受计算限制,实际上Q的元素不可能取无穷大。一般通过调整Q的元素,以获得良好的响应特性。R的元素可不调整。

控制律同式(7),使J最小的K即为最优反馈增益,可用MATLAB软件LQR函数求取,语句格式为K=LQR(A,B,Q,R)。

Q为:

(9)

图9 极点配置控制单级倒立摆系统响应曲线

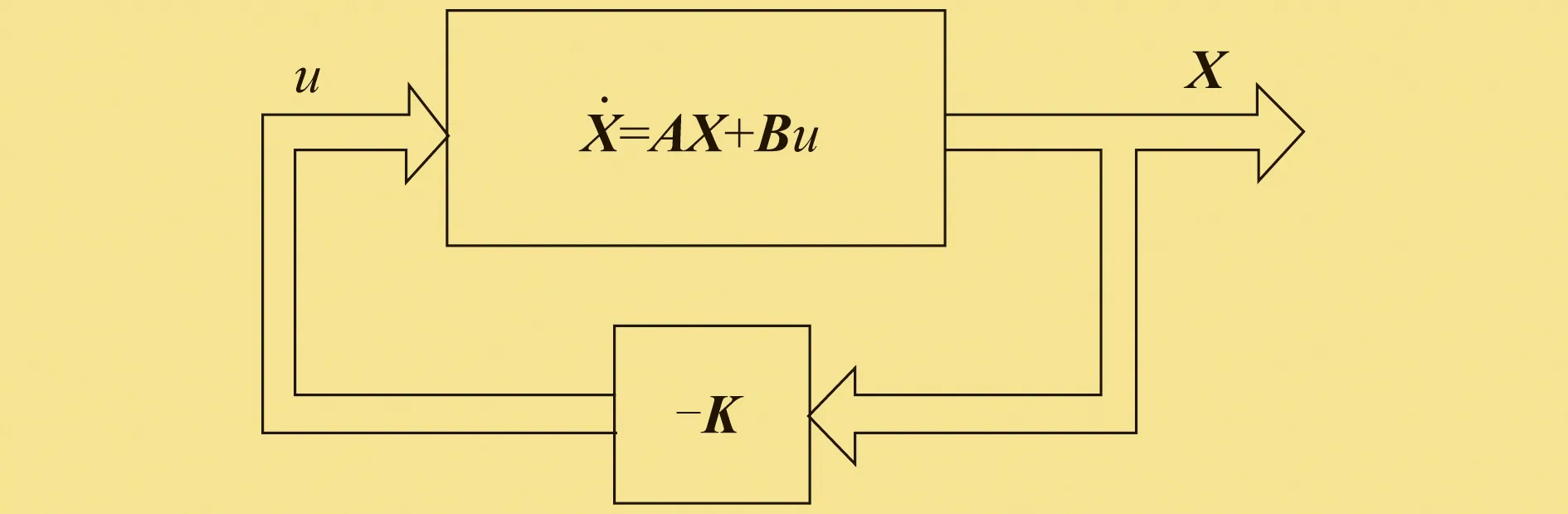
图10 线性二次型调节器控制原理

Q11为小车位移权重,Q33为摆杆角度权重。修改Q11、Q33可以得到不同的反馈增益矩阵K,从而实现不同的控制效果。当Q11为1,Q33为1,R为1时,最优反馈增益矩阵为[-1.000 0 -1.656 7 18.685 2 3.459 4]。当Q11为1 000,Q33为200,R为1时,最优反馈增益矩阵为[-31.622 8 -19.537 9 65.404 4 12.593 2]。

线性二次型调节器控制单级倒立摆系统仿真模型如图11所示,线性二次型调节器控制单级倒立摆系统响应曲线如图12所示。仿真时在模型中仍然引入幅值为0.5、作用时长为1 s的阶跃干扰信号。由图12可以看出,增大权重可以加快单级倒立摆系统的响应速度,减小超调量。

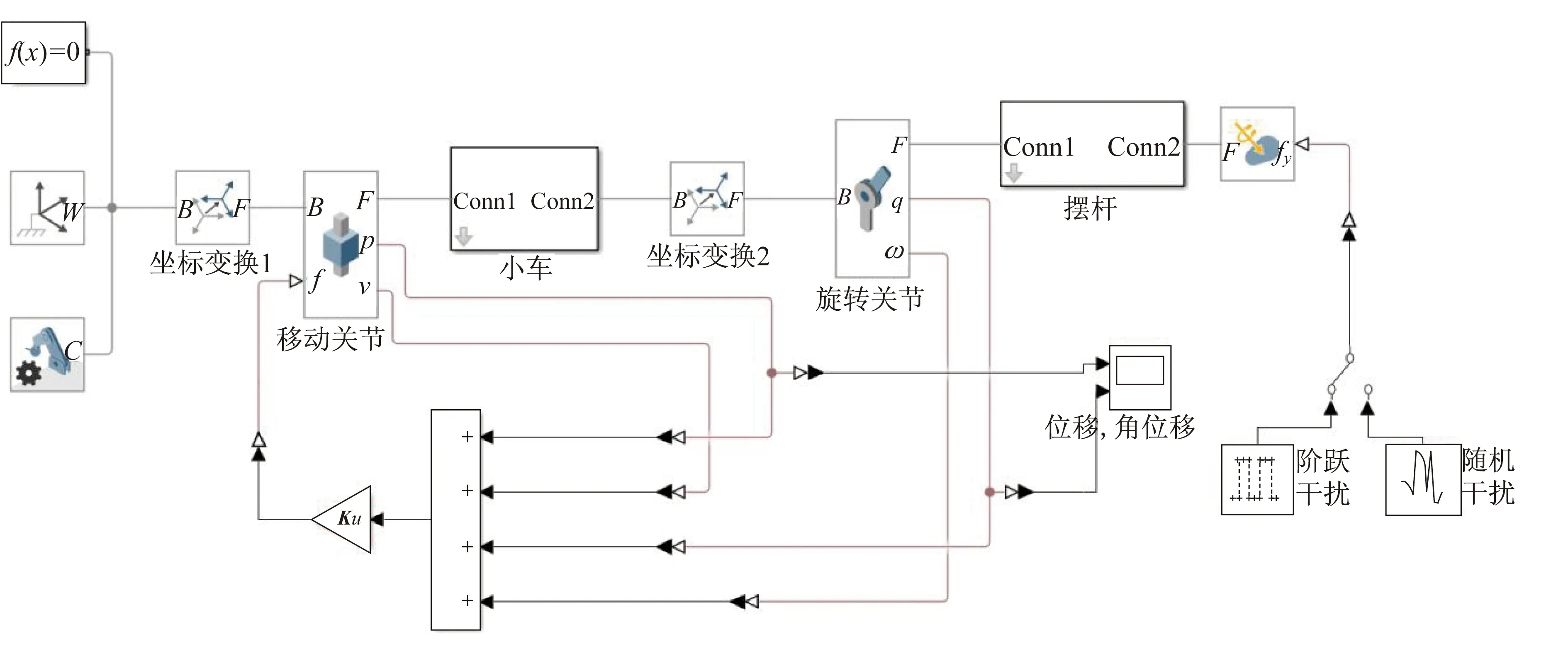
图11 线性二次型调节器控制单级倒立摆系统仿真模型

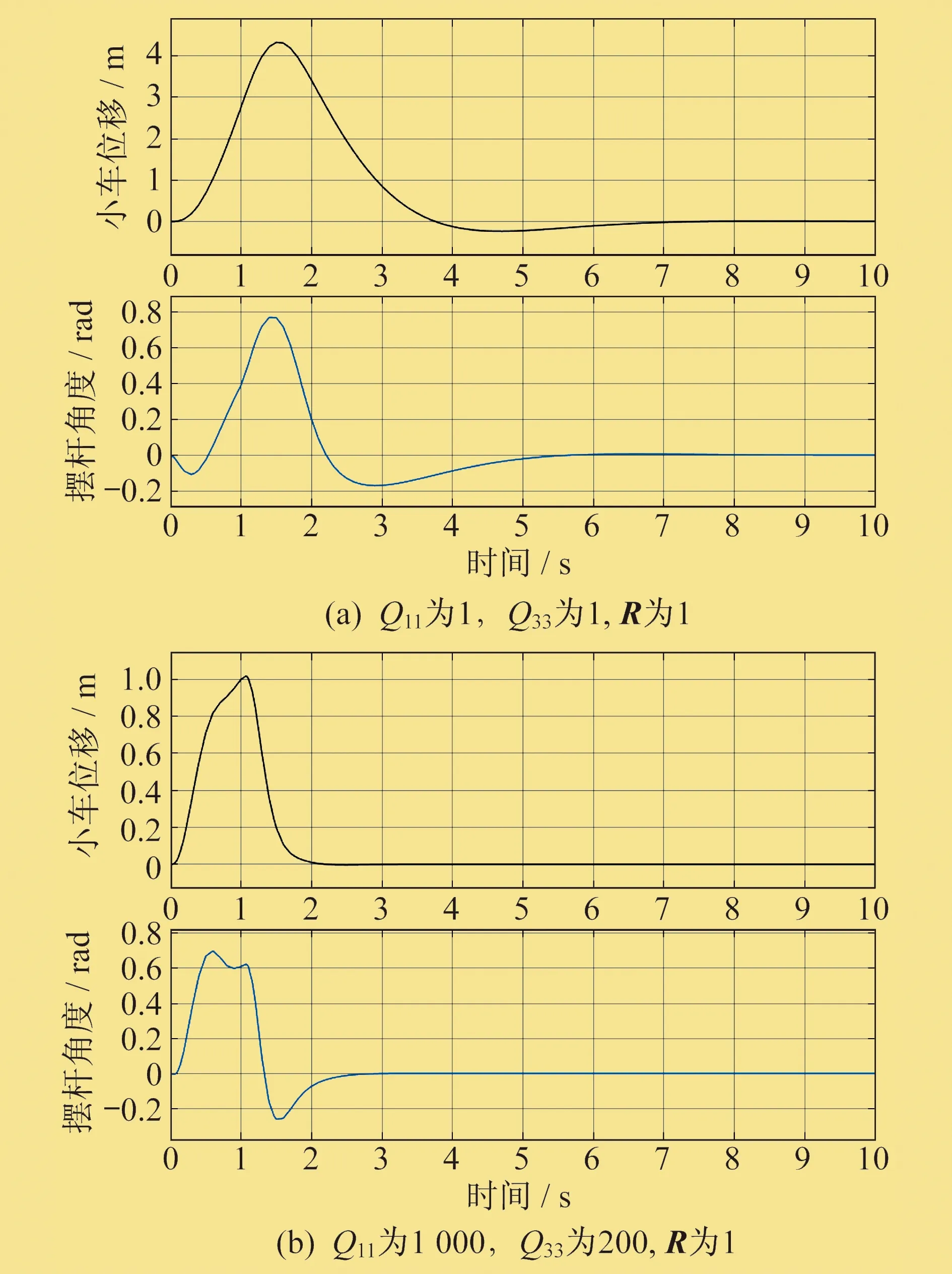
图12 线性二次型调节器控制单级倒立摆系统响应曲线

5 结束语

单级倒立摆系统是一个多变量、强耦合、不稳定非线性系统,针对这一系统,笔者设计双比例积分微分控制、极点配置控制、线性二次型调节器控制三种控制方案,进行了仿真分析和对比。分析结果表明,在一定的干扰范围内,单级倒立摆系统具有良好的抗干扰能力,可以通过调整控制律参数达到理想的控制效果。在实际应用中,可根据系统的具体指标要求选择适合的控制方案。