斜槛群不同透水率及不同高度对弯道水流的影响
2021-04-01张峻博张英超张靖王文康滕晓敏
张峻博,张英超,张靖*,王文康,滕晓敏
斜槛群不同透水率及不同高度对弯道水流的影响
张峻博1,张英超2,张靖2*,王文康2,滕晓敏2
1. 同济大学 土木工程学院, 上海 200092 2. 山东农业大学 水利土木工程学院, 山东 泰安 271018
为了研究不同透水率斜槛群对弯道水流特性的影响,本文进行了物理模型试验。通过试验所得数据,计算了最大横向水面差及相对最大横向水面差、水面差平均值、水面均匀度等水力学指标并进行了分析。结果表明:斜槛群的透水率越小,对弯道水流的改善效果越好;在正弦式斜槛群中,从最大横向水面差、水面差平均值、水面均匀度来看,斜槛的高度越高,改善弯道水流的效果越好。在余弦式斜槛群中,从最大横向水面差、水面差平均值、水面均匀度来看,斜槛过低过高对改善弯道水流的效果都不好。
斜槛群; 透水率; 高度; 影响
溢洪道是一种常用的泄水建筑物,由于受地形、地质、施工及运用条件等因素的限制,在实际工程中,常常需要设置弯道段。泄槽弯道处的水流受到离心力作用使凹岸水位变深,凸岸水位变浅,且因两侧边墙转向被迫发生偏转,从而产生急流冲击波。此外,弯道急流使得断面水深和动量波动范围大,水流流态差,增加了下游消能防冲的难度。目前,在实际工程中改善弯道水流主要有以下方法:渠底横向扇形抬高法[1]、消能栅与导流消能板法[2]、导流墩与糙条法[3]、淹没式导流屏法[4]、复曲线法[5]、渠底超高法[6]、斜槛法[7,8]等。Knapp[9]利用动量交换原理,在渠道底部设置突槛来调整弯道底部水流方向,改变了流场,平衡了凹凸岸水面差;魏炳乾[10]通过插入缓变曲线后发现可有效改善水流流态,减小对河道的冲刷;王鑫[11]对布置5道三种形式的斜坎进行了可行性研究,得出斜坎对消减弯道水面超高、改善水流流态有明显效果;滕晓敏[12]通过在溢洪道泄槽弯道段设置透水斜槛,发现透水斜槛对改善弯道水流的效果明显;杨金孟[13]通过在溢洪道泄槽弯道凹岸设置透水丁坝,使弯道水面均匀度增加,改善了弯道水流条件。通过傅灿[14]等人的试验研究发现,斜槛不合理布置或设计,不仅达不到消减急流冲击波的目的, 而且会更加恶化水流流态、降低下游消能设施的效率。且在急流情况下,斜槛背水一侧极易产生汽蚀现象,影响斜槛使用期限。
目前斜槛在工程中的应用是采用统一规格的多根斜槛组成斜槛群对水流进行调节。但为了找到最佳斜槛群的组合方法,本文研究不同透水率的斜槛群组合情况、以及不同高度的斜槛群组合对水流的调节能力大小,试图找到更合适的斜槛群组合方法,为工程建设中选择斜槛群提供参考。
1 试验方法
1.1 试验布置
本试验在山东农业大学水利实验室进行。试验系统包括地下水库、水泵、高位水池、供水管道、电磁流量计、稳流栅、渠道、模型试验区、尾水池、回水渠等设施。闸阀和电磁流量计用于控制和量测试验流量为100 m³/h,模型试验区用于布置试验模型和进行水深等指标的测量。
1.2 试验模型
试验模型溢洪道为矩形断面,宽500 mm,溢洪道底坡=0.02。轴线半径=1200 mm,弯道轴线长1500 mm,弯道前后泄槽均为直线连接段。弯道段均匀布置5道透水斜槛,位置分别为弯道轴线1/6、2/6、3/6、4/6、5/6圆弧处,斜槛轴线与弯道半径角度45°,见图1。透水斜槛采用圆形透水孔,斜槛尺寸见表1。

图 1 溢洪道弯道斜槛布置图

表 1 斜槛尺寸分布表
1.3 试验方案
本试验采用单因子变量法,控制其他因素不变,只研究某一个影响要素的改变对弯道水流的调整效果。本文主要讨论两个斜槛群的几何要素,分别为透水率和槛高。即高度相同、斜槛群的透水率不同以及透水率相同、斜槛群的高度不同。透水率计算公式为:透水孔总面积/斜槛总面积。为方便设计和施工,透水孔是成行列布置的,因此只能做到近似而不能做到完全相同。通过计算和设计,透水率差别较小。本试验所有方案流量均为100 m³/h。溢洪道弯道开始处的弗劳德数大于1.0,保证溢洪道弯道水流为急流。按照研究要素不同,本文试验分成两组。
1.3.1 斜槛群透水率组合方案本组合方案斜槛高度均为20 mm,根据不同位置斜槛的透水率分为4个方案,具体方案见表2所示。
1.3.2 斜槛高度方案本试验采用3个斜槛高度,分别为20 mm、30 mm、40 mm,具体方案见表3所示。

表2 斜槛群不同透水率组合方案
备注:表2中方案1斜槛群透水率变化规律为由小到大再减小,命名为正弦式斜槛群,方案2斜槛群透水率变化规律为由大到小再增大,命名为余弦式斜槛群。
Note: In table 2, the change rule of water permeability of scheme 1 is from small to large and then decreases, which is named sinusoidal sill group. The change rule of water permeability of scheme 2 is from large to small and then increases, which is named cosine sill group.

表3 斜槛群高度不同组合方案
备注:表3中方案5、8分别与表2中方案1和2相同。
Note: Scheme 5 and scheme 8 in table 3 are the same as scheme 1 and scheme 2 in table 2 respectively.
1.4 试验测量
试验测量内容包括水位、流量。水位测量采用精度为0.01 mm的数显水位测针。通过闸阀控制流量大小,采用中国开封仪表有限公司生产的E-magC型电磁流量计测量试验流量。
本试验共有18个测量断面,其中进口段布置3个测量横断面(0-0),(1-1),(2-2);弯道段均匀布置13个测量横断面(3-3),(4-4),…(15-15);出口段均匀布置2个测量横断面(16-16),(17-17)。沿水流方向对称布置5条纵向测线(包括左右岸边处、泄槽底板中心线处、距底板中心线两侧1/4槽宽处)纵横断面的交点为试验水位测量点。具体见图2。
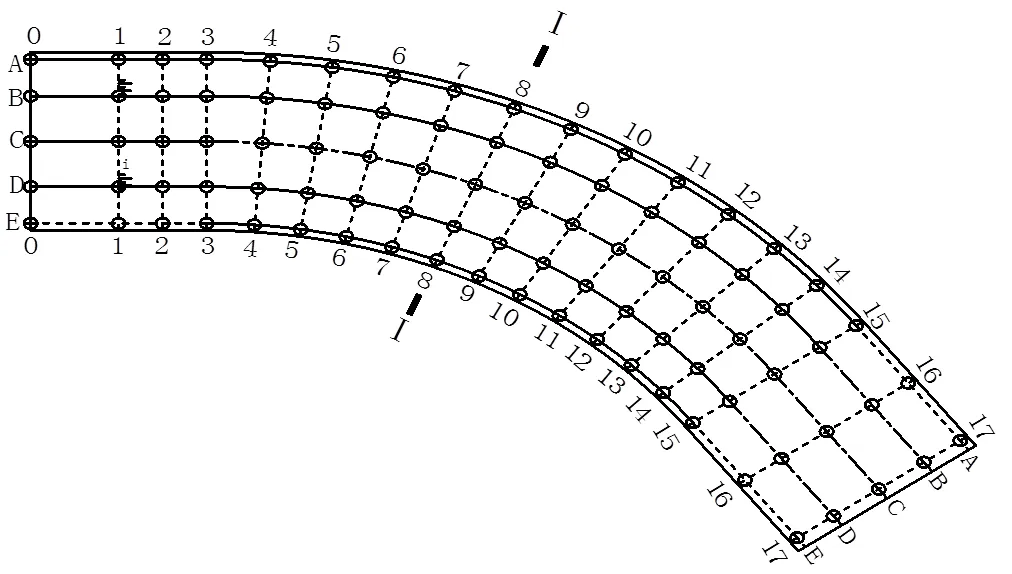
图 2 水位测量点布置图
2 结果与分析
2.1 分析指标
水流在溢洪道泄槽弯道上因离心力作用,泄槽弯道段水流产生横向环流现象,河道横断面水深发生变化,使凹岸水面雍高凸岸水面降低,从而在过水断面上形成横比降,致使水流不均匀。弯道段轴线设置不同透水率斜槛群的目的,就是为了改善这种水流现象。因此,分析弯道水流改善效果可用最大横向水面差及相对最大横向水面差、水面差平均值、水面均匀度等指标来反映。
2.1.1 最大横向水面差弯道横断面最大横向水面差是弯道各个横断面凹岸水深与凸岸水深差的最大值,反映弯道设置透水斜槛后对弯道凹凸岸最大水面差的改善情况,按下式计算:
∆max=max{|h1-h2|} (=1,2,…,5)(1)
式中:∆max为横断面最大横向水面差,mm;h1为弯道第个横断面凹岸水面深,mm;h2为弯道第个横断面凸岸水深,mm。
2.1.2 相对最大横向水面差
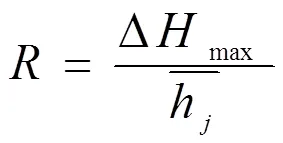
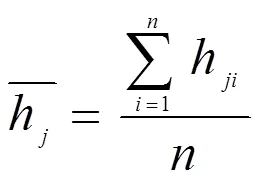
2.1.3 水面差平均值水面差平均值是同一方案各横断面水面差的平均值,从整体反映了设置透水斜槛后对溢洪道弯道水面的改善情况。

2.1.4 水面均匀度水面均匀度反映溢洪道横断面各点水深的均匀情况,用下式计算:

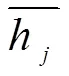
2.2 斜槛群透水率不同组合的水流改善效果分析
2.2.1 凹岸水面线通过四条曲线对比可以看出,余弦式斜槛群的布置方法具有最低的凹岸水面线,而正弦式斜槛群的布置方法凹岸水面线相对较高,大透水率的斜槛群凹岸水面线较低,如图3所示。

图 3 斜槛群透水率组合方案的凹岸水面线
具体分析如下:(1)对比方案1和方案2,方案1中小透水率的斜槛布置在最前部,引发水流壅高,并在进入弯道中部乃至后部时在较高的范围内进行水面波动,而方案2透水率较大,水流壅高被有效减弱,进而后续波动发生在较低的水位基础上。(2)对比方案1和3,两者具有相同的第一根斜槛的透水率,但后续斜槛的透水率不同造成了凹岸水面线变化不同。方案1水面波动比方案3更加剧烈,且普遍凹岸水面线较高。产生这个现象的原因在于方案1各斜槛的透水率不均,造成水流在过弯道的各个位置处所遭受的阻力不同,过流通道面积和位置也不同,因此水面线变化更加剧烈。(3)同样对比方案2和4,方案2水面线变化也相对4更复杂。(4)由于水流过弯时的弯道水流效应,凹岸水面线比凸岸水面线高,泄槽边墙高度往往需要根据此进行加高,导致使用的材料增加。故凹岸水面线低比较有利减少边墙材料使用,并使水流均匀过弯,对比四组图线,方案2和方案4具有最低的水位,说明大透水率布置时的凹岸水位调节作用最好。
2.2.2 凸岸水面线相对于凹岸水面线,凸岸水面线在不同方案时的差别更加明显。通过四条曲线对比可以看出,大透水率的斜槛群凸岸水面线较低,透水率不变的斜槛群产生四者中最高和最低的凸岸水面线。如图4所示。
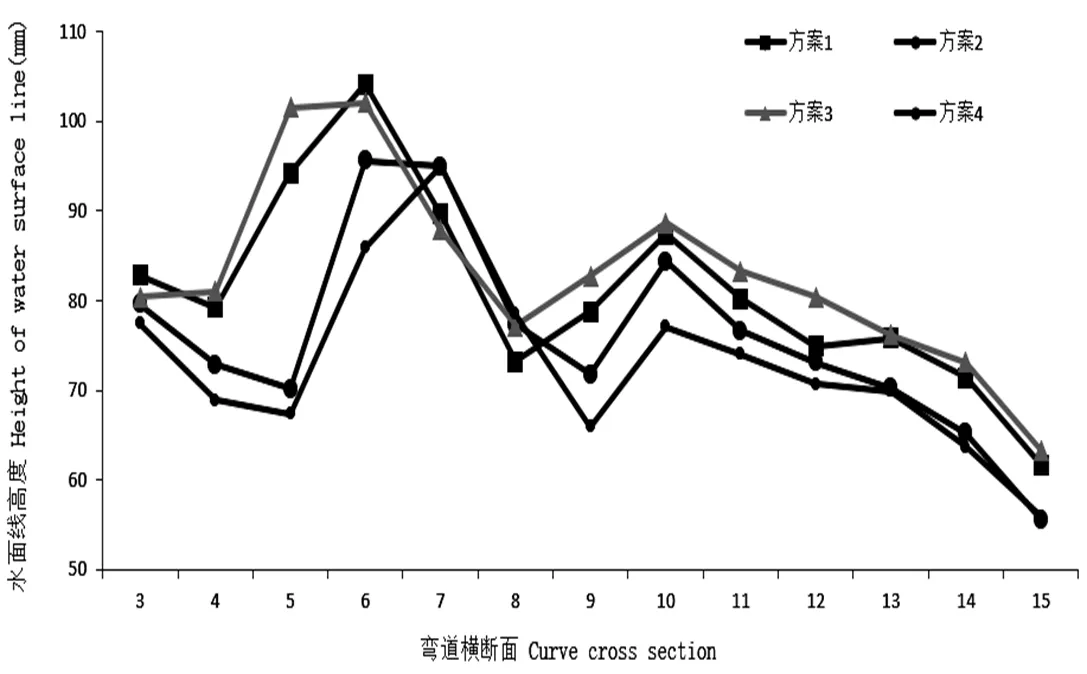
图 4 斜槛群透水率组合方案的凸岸水面线
四条线明显分成两组,其中方案1、3的凸岸水面线相近,而方案2、4的凸岸水面线相近。具体分析如下:(1)对比方案1和2,方案1水面线位于方案2水面线上方,因方案1首条斜槛透水率小于方案2首条斜槛透水率,导致方案1水面壅高值大于方案2。(2)对比方案1和3,两者具有相同的第一根斜槛的透水率,水面线变化基本一致,在弯道中、后部方案3水位稍高、波动略小于方案1,这是由于进入弯道中部之后,方案1中斜槛透水率发生变化,引发水流不稳定,故产生比均匀透水率方案(方案3)略强的波动。(3)对比方案2和方案4,两者具有相同的第一根斜槛的透水率,但后续斜槛的透水率不同造成了凸岸水面线变化不同。(4)由于水流过弯时的弯道水流效应,凸岸水面线比凹岸水面线低,有时甚至出现露底现象,导致底板破坏。故凸岸水面线高比较有利水流均匀过弯,对比四组图线,方案1和方案3具有最高的水位(两者差别不大),说明小透水率变化布置时的凸岸水位调节作用最好。
2.2.3 最大横向水面差及相对最大横向水面差最大横向水面差反映了同一断面凹凸岸水面之间的最大差值,若水流绝对均匀,最大横向水面差应为0,故该值越小表示水流过弯越均匀。相对最大横向水面差反映了每个断面的最大横向水面差占水深平均值的百分比,比例越小表示水流流态越好。
从图5可得,在13组数据中:方案3有7组最大横向水面差最小,占53.8%;方案1和方案4各有1组最大横向水面差最小,占7.7%;方案2有3组最大横向水面差最小,占23.1%。由此说明,方案3对最大横向水面差的改善效果最好。
从图6可得,相对最大横向水面差小于50%的数据中,方案1占1组、方案2占2组、方案3占3组、方案4占1组;相对最大横向水面差小于30%的数据中,方案1占1组、方案3占1组、方案2、方案4占0组。

图 5 斜槛群透水率组合方案的最大横向水面差

图 6 斜槛群透水率组合方案的相对最大横向水面差
通过对比分析可得:(1)小透水率的最大横向水面差好于大透水率情况;(2)透水率的改变不利于水流稳定,故水面产生了较大改变,因而方案1相对于方案3的布置水面差略大。
2.2.4 水面差平均值水面差平均值是同一方案各横断面水面差的平均值,从整体反映了设置透水斜槛后对溢洪道弯道水面的改善情况。
从图7中可得,在斜槛群高度相同、透水率组合不同的情况下,方案3弯道段水面差平均值最小,为15.0 mm,对水流流态的调整效果最好;方案4弯道段的水面差平均值最大,为22.2 mm,对水流流态的调整效果最差;方案1与方案2弯道段的水面差平均值相差不大,分别为17.5 mm、19.1 mm,对水流流态的调整效果较好。由此说明,方案3对水面差平均值的改善效果最好。
2.2.5 水面均匀度水面均匀度反映了溢洪道横断面各点水深的均匀情况。若水流绝对均匀,水面均匀度应为100%,故该值越大表示水流过弯越均匀。

图 7 斜槛群透水率组合方案的水面差平均值
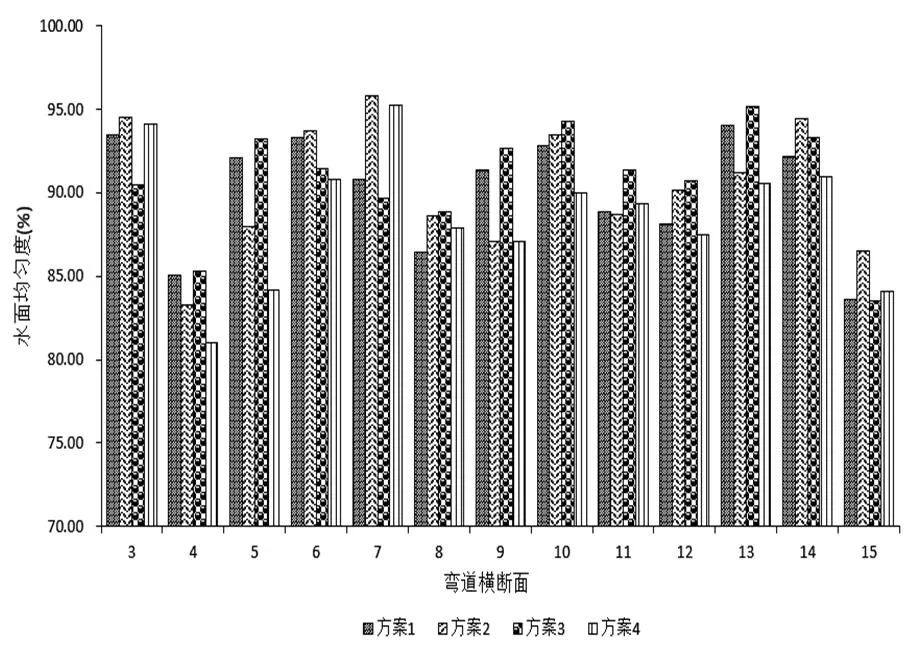
图 8 斜槛群透水率组合方案的水面均匀度
从图8可以看出,水面均匀度大于85%的数据中,方案1占12组、方案2占12组、方案3占12组、方案4占10组;水面均匀度大于90%的数据中,方案1占8组、方案2占7组、方案3占9组、方案4占6组;水面均匀度大于95%的数据中,方案1占0组、方案2占1组、方案3占1组、方案4占1组。
通过对比分析可得:(1)小透水率的水面均匀度好于大透水率情况;(2)透水率的改变不利于水流稳定,故液面产生了较大改变,因而方案1相对于方案3的布置水面均匀度略小。
2.3 正弦式、余弦式斜槛群对水流改善效果分析
在斜槛群透水率变化基本一样的情况下,为分析斜槛群高度的影响,将方案5、6、7(表3);方案8、9、10(表3)进行数据整理和分析,得到以下指标和结论。
2.3.1 凹岸水面线将正弦式、余弦式斜槛群的凹岸水面线绘制成线,如图9、10所示。

图 9 正弦式斜槛群凹岸水面线
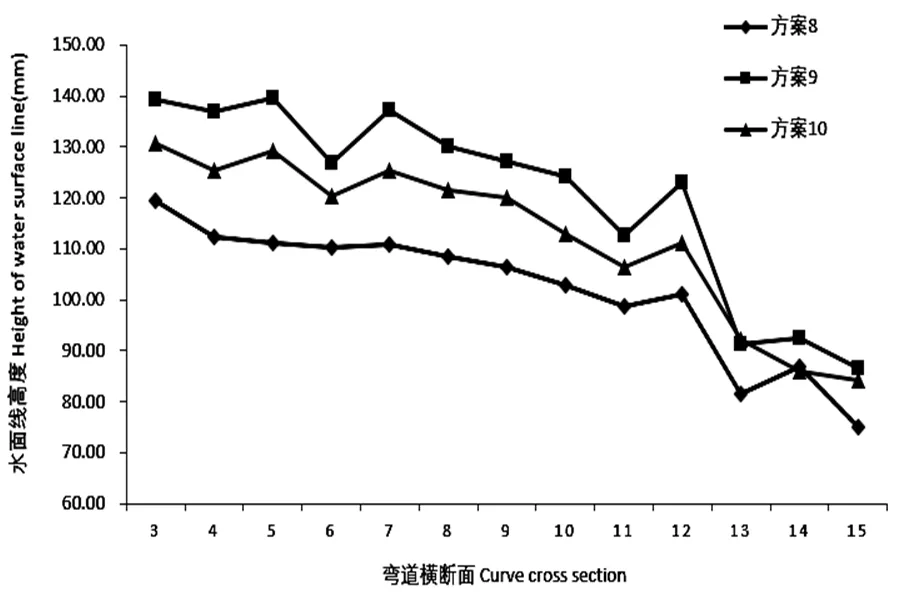
图 10 余弦式斜槛群凹岸水面线
通过图9可以看出,凹岸水面线大小与斜槛高度呈正相关。方案5具有最低的凹岸水面线,方案7具有最高的凹岸水面线。具体分析如下:(1)对比方案5、6、7,斜槛的高度越高,引发水面线壅高越明显,因此方案7具有最高水面线。在弯道前部和中部,3组方案的水面波动规律相近。(2)因泄槽边墙的高度需在凹岸进行加高,方案5具有最低水面线,说明斜槛高度较低时对凹岸水位调整作用好。
通过图10可以看出,方案8具有最低的凹岸水面线,方案9具有最高的凹岸水面线。对比方案8、9、10,斜槛的高度较高,引发水面线壅高越明显、且变化规律相同。
2.3.2 凸岸水面线相对于凹岸水面线,凸岸水面线在不同方案时的差别更明显。正弦式、余弦式斜槛群的凸岸水面线沿程变化如图11、12所示。

图 11 正弦式斜槛群凸岸水面线

图 12 余弦式斜槛群凸岸水面线
由图11可以看出,方案5由于槛高在三者中最低,对凸岸水位的调整最小,因而其凸岸水面线最低,且容易引发波动;方案7具有最高的槛高,对凸岸水位调整效果最明显,且水面较为均匀;方案6具有中间槛高,调整效果居中。
由图12可以看出,方案9和10的凸岸水面线具有相同变化规律;方案8由于槛高在三者中最低,对凸岸水位的调整最小,因而其凸岸水面线最低,且容易引发波动;方案9具有较高的槛高,对凸岸水位调整效果最明显,且水面较为均匀;方案10具有最高的槛高,调整效果居中。由此看出槛高时调整效果较好。
2.3.3 最大横向水面差及相对最大横向水面差最大横向水面差及相对最大横向水面差的指标如图13、14所示。
由图13可得:方案5有0组最大横向水面差最小,占0%;方案6有3组最大横向水面差最小,占23.1%;方案7有10组最大横向水面差最小,占76.9%。由此说明,正弦式斜槛群中方案7对最大横向水面差的改善效果最好。方案8有0组最大横向水面差最小,占0%;方案9有8组最大横向水面差最小,占61.5%;方案10有4组最大横向水面差最小,占30.8%。余弦式斜槛群中方案9对最大横向水面差的改善效果最好。
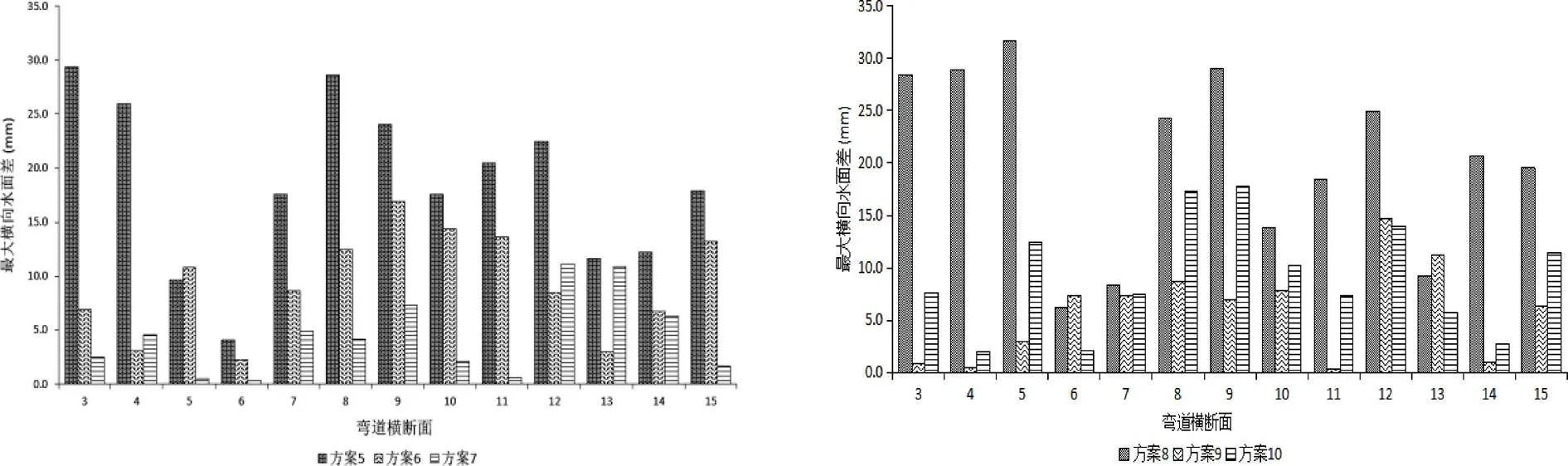
图 13 最大横向水面差

图 14 相对最大横向水面差
由图14可得:相对最大横向水面差小于50%的数据中,方案5占1组、方案6占3组、方案7占4组、方案8占3组、方案9占3组、方案10占3组;相对最大横向水面差小于30%的数据中,方案5占1组、方案6占1组、方案7占3组、方案8占0组、方案9占3组、方案10占3组。
对比方案5、6、7分析可得:高度的增加利于水流稳定,斜槛高度越高,最大横向水位差值越小;对比方案8、9、10分析可得:方案9相对最大横向水面差的改善效果最好。
2.3.4 水面差平均值正弦式、余弦式斜槛群的水面差平均值指标如图15所示。
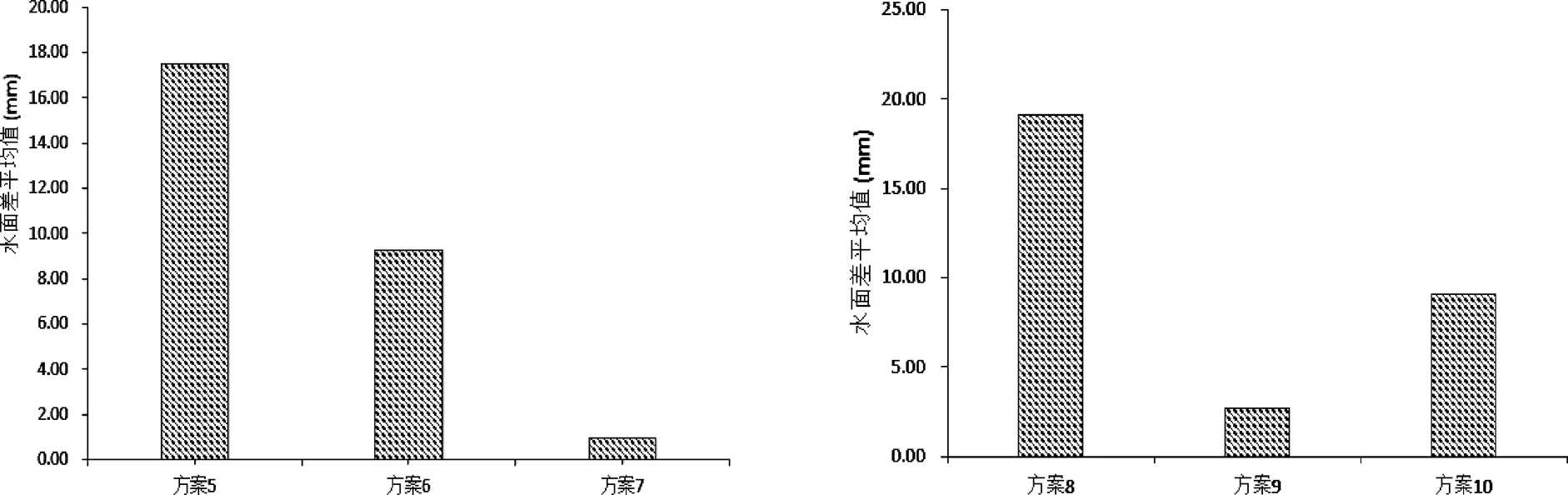
图 15 水面差平均值
由图15可知,在透水率相同、斜槛群高度不同的情况下,正弦式斜槛群中方案5斜槛群水面差平均值最大,为18.58 mm,对水流流态的调整效果相对最差。方案7斜槛群水面差平均值最小,为4.33 mm,对水流流态调整效果相对最好。
余弦式斜槛群中方案8斜槛群水面差平均值最大,为19.12 mm,对水流流态的调整效果最差;方案9斜槛群水面差平均值最小,为2.74 mm,对水流流态调整效果最好。
2.3.5 水面均匀度正弦式、余弦式斜槛群的水面均匀度指标如图16所示。

图 16 水面均匀度
从图16可以看出,正弦式斜槛群中水面均匀度大于90%的数据中,方案5占7组、方案6占9组、方案7占11组;大于95%的数据中,方案5占0组、方案6占8组、方案7占6组。
余弦式斜槛群中水面均匀度大于90%的数据中,方案8占7组、方案9占10组、方案10占10组;大于95%的数据中,方案8占1组、方案9占6组、方案10占5组。
通过对比分析可得:(1)斜槛群高度高的水面均匀度好于斜槛群高度低的情况;(2)高度低的斜槛群因壅水高度较低,凸岸水位不能得到有效提高,故水面差平均值低于槛高的斜槛群。
3 结论
本试验研究得到以下结论:(1)不同透水率斜槛群对水流改善有一定影响,在其他条件相同时,斜槛群的较小的透水率使弯道水流的均匀度更大一些。(2)透水率按位置不同的布置方式中,第一根斜槛的透水率大小对调整效果的影响最大,其调整效果与按照第一根斜槛的相同透水率布置效果基本相同。(3)从水面差平均值、水面均匀度来看正弦式斜槛群的布置形式调整效果优于余弦式斜槛群的布置形式。(4)从最大水面差、水面差平均值、水面均匀度3个指标分析发现:采用正弦式斜槛群的布置形式时,斜槛的高度越高,改善弯道水流的效果越显著;当采用余弦式斜槛群的布置形式时,斜槛过低过高对改善弯道水流的效果都不好。此外,斜槛群的组合方式多种多样,若寻求最佳方案、还需进一步试验研究。
[1]西北水利科学研究所.明渠陡槽急弯上冲击波最大水深计算及弯道底部扇形抬高克服方法报告[R].1961.
[2]邱秀云,侯杰,孙涛,等.一种消除陡坡弯道急流冲击波的新措施[J].水力发电,1998(11):18-20,64
[3]孙娟,陈晓梅.导流墩和糙条对溢洪道弯道水流的调整作用[J].新疆水利,2001(6):6-9
[4]姚仕明,金琨.淹没式导流屏在河流治理中的应用[J].长江科学院院报,2001,18(4):18-21
[5]黄春花,孙颖,陈肇和,等.急流弯道双曲底板的体形设计[J].水利学报,2003(8):1-5
[6]周斌,宋天文,龚爱民,等.渠底超高法和弯曲导流板法在凤凰水库溢洪道的应用[J].水电能源学,2007(5):89-90,60
[7]傅灿,邱勇,周卫霞.斜槛法在消减弯道急流冲击波中的应用[J].陕西水利,2010(3):102-103
[8]周星,杨校礼,高峰.斜槛法在山区弯道河流消能设计中的应用[J].水电能源科学,2014,32(3):126-128,69
[9]Knapp RT. High-velocity Flow in Open Channels: A Symposium: Design of Channel Curves for Supercritical Flow [J]. Transaction of the Amercican Society of Civil Engineers, 2014,116:393-400
[10]魏炳乾,严培,刘艳丽,等.插有缓变曲线弯道水流运动的三维数值模拟[J].长江科学院院报,2016,33(6):1-7
[11]王鑫,张宗孝,严培,等.应用斜坎改善弯道流态的可行性研究[J].西北农林科技大学学报(自然科学版),2017,45(1):197-204
[12]滕晓敏,陈威,杨金孟,等.透水斜槛对溢洪道泄槽弯道水流改善效果试验[J].南水北调与水利科技,2018,16(5):171-178
[13]杨金孟,滕晓敏,陈威,等.单个透水丁坝对溢洪道泄槽弯道水流流态影响试验研究[J].水电能源科学,2018,36(9):102-106
[14]傅灿,邱勇,余雄杰,等.一种改善溢洪道陡槽弯道水流流态的措施研究[J].南水北调与水利科技,2010,8(1):49-51
The Influence of Different Water Permeabilities and Heights of Inclined Sill Group on Flow in Bend
ZHANG Jun-bo1, ZHANG Ying-chao2, ZHANG Jing2*, WANG Wen-kang2,TENG Xiao-min2
1.200092,2.271018,
In order to study the influence of the inclined sill group with different permeability combinations on the flow characteristics of the bend, a series of physical model tests were carried out in this paper. Based on the experimental data, the hydraulic indexes such as the maximum transverse water surface difference and the average water surface difference relative to the maximum transverse water surface difference were calculated and analyzed. The results show that the smaller the permeability of the inclined sill group is, the better the improvement effect of the water flow in the bend is. In sinusoidal sill group, the higher the height of the inclined sill is, the better the effect of improving the water flow in the curve will be from the perspective of the maximum horizontal water surface difference and average water surface difference. In cosine sill group, from the point of view of the maximum transverse water surface difference and the average water surface evenness of the water surface difference, too low and too high sill is not good for improving the water flow in curves.
Inclined sill group; permeability; height; influence
TV135
A
1000-2324(2021)01-0054-09
10.3969/j.issn.1000-2324.2021.01.010
2019-09-01
2019-11-20
山东省自然科学基金青年基金(ZR2020QE286);天津大学水利工程仿真与安全国家重点实验室开放基金(HESS-2008)
张峻博(1997-),男,硕士在读,研究方向为水文与水资源工程. E-mail:1740082836@qq.com
Author for correspondence. E-mail:jing16@sdau.edu.cn
