单侧供热汽车烘干房气流组织数值模拟研究

李会知,侯孟言,邢金超

单侧供热汽车烘干房气流组织数值模拟研究

李会知1,侯孟言1,邢金超2

1. 郑州大学 土木工程学院, 河南 郑州 450001 2. 郑州力之天农业科技有限公司, 河南 郑州 450001

本文以一种新型的单侧供热的大型运猪汽车烘干房为研究对象，通过现场实测和Airpak数值模拟相结合的方法，研究该烘干房的气流组织，分析送风口位置、送风速度的不同对烘干房温度场及烘干质量的影响。研究表明送风口1和送风口2的位置分别为1=2.8 m、2=12.65 m，送风速度1=4.5 m/s、2=5 m/s时，烘干房内温度不均匀系数最小，温升时间最短，气流组织最优。在此基础上分析了温度和速度分布特征，为后续研究提供参考。

汽车; 烘干房; 气流组织; 数值模拟

近期非洲猪瘟等病毒造成养猪场生猪批量死亡，说明猪场的生物安全极为重要，大型养猪场迫切需要更为严格的生物安全管理体系，运猪汽车作为养猪场内运送生猪的唯一交通工具，是猪场生物安全的最大威胁之一[1-4]，需要对其进行彻底的清洗消毒，经试验研究表明在高温环境下，绝大多数猪只病毒在高温下能完全失活[5-7]，因此需要对清洗后的车辆进行高温烘干，这样既可以有效防止病菌的传播，也能使车辆快速干燥，提高车辆利用率。郑州力之天农业科技有限公司和郑州大学合作研发的运猪汽车烘干房结构形式也在不断改进，带耳房形式的烘干房两侧墙面的热风出风口速度较低，升温时间较长，且在投入使用后，耳房内的风机持续在高温条件下工作，易缩短使用寿命，降低了经济效益。因此后续研发了新的结构形式的烘干房——单侧供热运猪汽车烘干房。

烘干房内合理的送风系统能形成比较均匀而稳定的温度场，有利于车身的快速烘干，提高烘干质量。本文基于CFD方法，利用AIRPAK软件，对一种新型的运猪汽车烘干房进行模拟研究，将模拟结果与实测数据进行对比分析，通过改变烘干房送风口的位置、送风速度对烘干房室内流场进行模拟，对各种工况下的温度场和速度场进行对比分析，对烘干房结构进行合理优化，为后续运猪汽车烘干房的研究提供参考。

1 建立烘干房模型

1.1 烘干房实体模型及网格划分

本文以一种新型的单侧供热的运猪汽车烘干房为研究对象，运猪车辆用烘干房由烘干房主体室和燃烧装置设备间构成，室外新风进入设备间内的燃烧室燃烧后，燃烧后的热风与烘干房内回风在设备间的混合室混合，混合后的热风由风机通过送风管道直接输送到烘干室，运猪汽车的烘干在烘干室内完成，烘干室的内壁墙板进行保温处理。本文仅研究烘干室内气流组织情况，将烘干房简化后的模型如图所示。

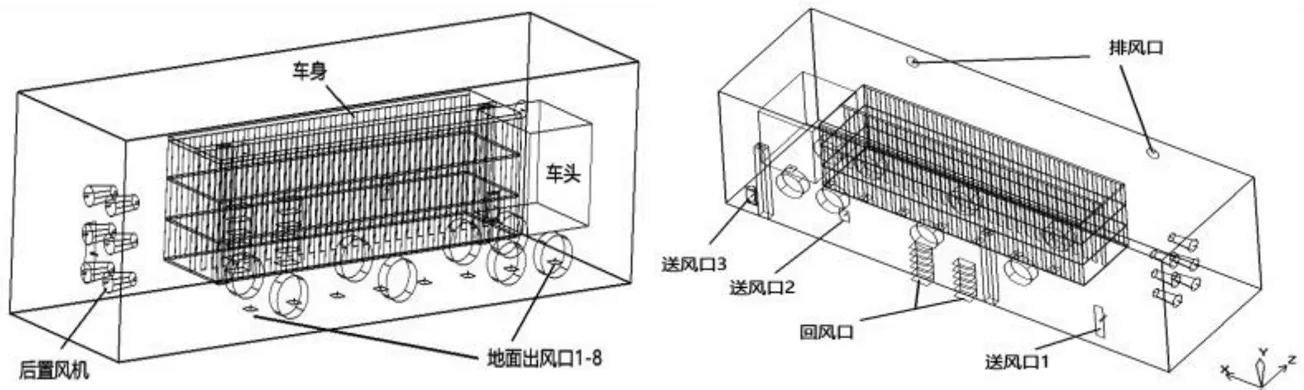
图 1 烘干房的简化模型

烘干房大小为（长×宽×高）16.5 m×5 m×5.2 m，其总建筑面积约为82.5 m²，此烘干房摒弃了之前带耳房构造的烘干房结构形式，避免了热风在耳房内二次散失热量。对车身加热方式主要方式为对流传热，对流传热按照送风方式分类，一般可分为“下送上回”、“上送下回”、“侧上送侧下回”、“侧下送侧上回”等送风方式[8-9]，由于运猪汽车体型较大，且汽车底盘结构复杂、不易烘干，本实验采用“侧下送侧上回”与“下送侧上回”结合的送风方式，并在此基础上，在烘干房内汽车尾部处加设六台后置风机，当设备启动后能加快室内气流循环，高效利用热量，提高烘干效率。

图 2 烘干房风口布置图

简化后的模型左侧墙两端共有三个送风口，右侧墙上方有两个排风口（直径为0.43 m），地面中心线均布八个出风口，左侧墙中部有两个回风口，其回风在燃烧室内和燃烧后的新风混合以便再次送入室内。送风口1-3的中轴线距烘干房入口侧边界的距离分别为2.535 m、12.01 m、15.53 m，具体参数如下表所示。

表 1 风口尺寸表

2 数学模型及参数设置

2.1 数学模型

在进行模拟时，烘干房内热空气连续相的流动换热是基于连续性方程、动量方程、能量方程和计算湍流的方程进行数值模拟[10,11]。连续性方程如下式:

能量守恒方程：可描述为流体微团内能变化率为流入微团的净热流量以及体积力和表面力对流体微团的做功功率的和。

动量守恒方程：当方程的对流项均采用散度形式表示时，这种方程为守恒式的控制方程。

(4)

(5)

2.2 参数设置

在使用数值模拟软件Airpak进行模拟时，假设烘干室壁面传热采用设置热流密度的边界条件，忽略由流体黏性力做功引起的耗散热，忽略室内车身和墙壁之间的辐射作用，流体按连续介质处理，将该传热过程视为非稳态湍流传热问题，时间步长设置为3 s，每十个步骤保存一次，指定统一的时间步长，模拟时间为0~1800 s，根据测量结果设置模拟条件室外温度为16.89 ℃，室内设计温度为70 ℃，经实地测量得各送风口风速及温度如下表所示。

表 2 送风参数表

烘干房共计有六台后置风机在室内循环送风，经实地测量得每个后置风机入口处的风速约为23 m/s，其循环风量约为1.79 m³/s。地面出风口每个风口的循环风量设置为0.36 m³/s，设置室内初始温度与外界环境温度相同。车身材料以钢为主，墙体为150 mm厚加芯复合聚苯板，外抹灰砂浆。建筑保温材料的热工设计计算应当采用计算值，参考现行的《民用建筑热工设计规范》（GB50176）得到烘干房墙体的保温材料的传热系数，烘干房大门使用冷库保温门，以泡沫板为保温层，两侧面板材料为彩钢板，保温门的门厚约150 mm。墙体材料传热系数如下表所示。

表 3 墙体传热系数表

对烘干房进行模拟时采用了标准-双方程湍流模型，方程采用有限体积法进行离散，网格划分采用六面体非结构化网格，对流动复杂的地方（比如轮胎、后置风机处）进行网格加密处理，划分完网格数为660764，网格质量良好。

3 测量方案及模拟分析

3.1 测量方案及评价指标

烘干房高温烘干的目的之一在于灭杀车身上的病菌，防止疫病在猪群内的传播，在运送生猪时，两侧栏杆与生猪直接接触，是最易传播疫病的区域，因此本次实验将测点布置车厢两侧栏杆和中间栏杆处，分三层布置，最底层和中间层每层布置九个测点，最顶层布置两个测点于中轴线处，共计20个测点，第一层到第三层测点布置高度分别为1.4 m、2.4 m、3.8 m，从左到右栏杆距左墙的距离分别为1.3 m、2.5 m、3.7 m，测量方案布置如图3，使用的测量仪器为精创温湿度自记仪，测得烘干房内初始平均温度为16.89 ℃。

运猪汽车烘干房运行中，室内风速跟温度较高，设备启动时，人员不得停滞在烘干房内，使用温湿度自记仪记录数据，设备设置为每隔三十秒记录一次，要求所有的测点均能保持在70 ℃~80 ℃之间，且维持时间不少于20 min，才能有效灭杀大部分生猪易感染病菌[4]。

为客观评价运猪汽车烘干房内的气流组织形式和分布特征，本文选取测点的温度不均匀系数和速度不均匀系数作为主要参考指标，不均匀系数值越小，气流分布越均匀[5]。不均匀系数公式如下：

3.2 模拟分析

将测点的模拟结果与测量结果的平均值进行对比，如图4，发现不同位置的测点升到70摄氏度的温升时间有差距，模拟温升段达到70 ℃时需240 s，实验测得温升段达到70 ℃约500 s，这是由于烘干房刚开始运作时，燃烧机燃烧后的空气进入设备间的混合室与冷空气混合，首先加热混合室内的空气，刚开始的几分钟内烘干室的送风口送风温度暂未达到90 ℃，在燃烧一段时间后，出风口的送风温度才趋于稳定状态。用AIRPAK进行数值模拟时，模拟结果的各测点温升时间比测量结果大大缩短，但室温达到70摄氏度时，即室内流场充分发展后的稳定结果与测量结果准确度较高，在烘干室运行十分钟到第三十分钟内，这二十分钟内模拟数据与实验数据误差在0.1%以内，且满足烘干房使用要求，可使用AIRPAK进行后续模拟研究及优化。

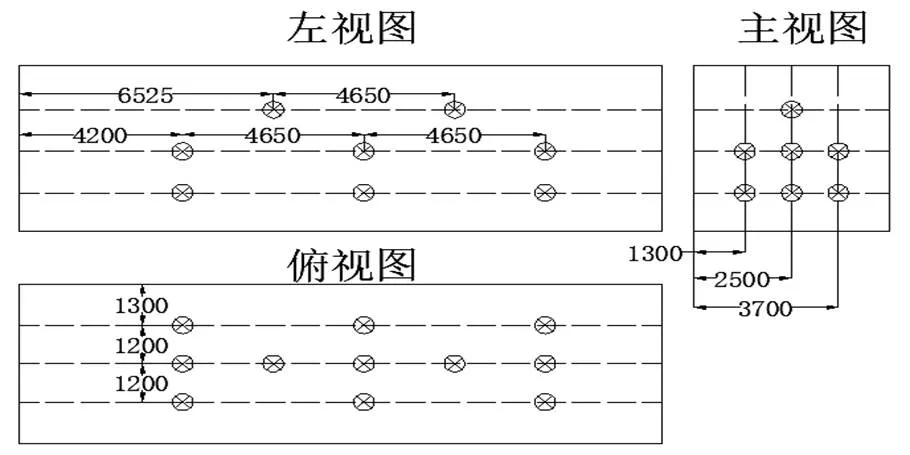
图 3 温度测点布置图

图 4 模拟与实验结果的对比曲线图

根据模拟结果显示，烘干房的温度在达到70 ℃后，随时间缓慢上升，车身栏杆的平均温度在75~80摄氏度之间。室内温度场稳定后，在烘干房运行稳定后取=30 min时的不同高度的平面=1.4 m、=2.4 m，分析第一层测点所在平面=1.4 m和第二层测点所在平面=2.4 m温度分布云图，可以由图5看出烘干室有送风口侧的整体温度要高于另一侧部分的温度，随着车身高度的增高，烘干房内的整体温度变大，靠近车笼栏杆处的温差变小，整体温度越均匀。

送风口2的热风遇到由后置风机向车身两侧流动的气流就改变了送风方向，沿着车身向车头处流动，热风很难到达车身右侧栏杆处，因此右侧后方栏杆处温度偏低。可由图5看出云图上送风口2旁一部分半圆形区域温度较高，因此可以通过改变送风口2的位置进行优化，提高送风口2的热量利用率，使温度更均匀。

图 5 Y=1.4 m处平面温度分布云图

图 6 Y=2.4 m处平面温度分布云图

送风口1的热风射流到达后置风机出风口前部区域时受到强力风作用，由车笼尾部向前部流动，由于两排后置风机风速高，两股气流相互作用一边向车头位置流动一边向两侧扩展，当到达车笼前板处向两侧流动（如图7），与绕过车头两侧气流相遇，在车头右侧轮胎处形成小涡旋区；而靠近送风口侧气流向车厢外流动于栏杆处遇到送风口2的热风射流，因此送风口2的热气流大部分都沿墙向车头前部流动。

截取=2.5 m平面及=3 m平面的速度矢量图分析烘干室内气流流动趋势，可由图6看出后置风机前部出风气流由车尾向车前部流动，一部分与地面出风口的气流相遇，送风口2和送风口3的热风在后置风机高速气流作用下向车前部流动，车底气流在压强作用下向车尾部流动，与后置风机的气流在车尾底部形成对流；一部分吹向车笼内部，遇到车笼前挡板便向车身两侧斜向流动（如图7）；车前部的热空气又通过车顶上方向车尾流动，再流入后置风机尾部风口，通过风机加速循环，自风机前部出风在烘干房内部形成一个气流循环。结合图6及图7的气流循环图可得室内气流组织较为合理，可针对送风口的位置及送风速度进行研究分析。

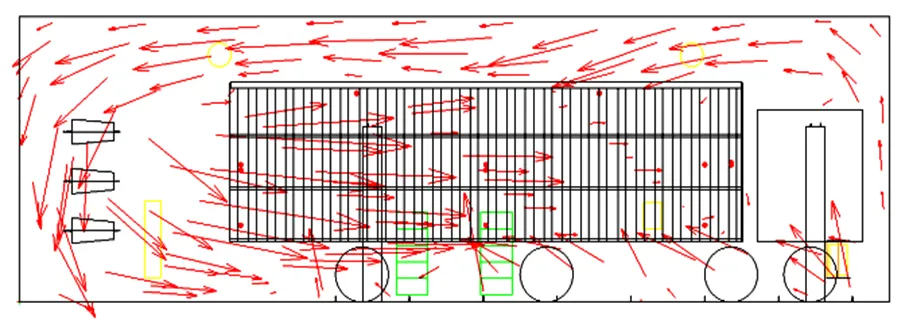
图 7 Z=2.5 m平面的速度矢量图

图 8 Y=3 m平面的速度矢量图

4 优化设计

4.1 风口位置的优化分析

针对模拟结果，选择改变送风口1和送风口2的位置作为优化研究对象。烘干室燃烧装置设备间有两个燃烧室，间隔为1 m，最长对角为2.24 m，送风口1中轴线的位置1=2.535 m，送风口2中轴线的位置为2=12.01 m，考虑到回风口及后置风机的位置，设计24种工况将模拟结果分组进行对比分析，模拟工况参数如表4所示，其中工况3为原模拟结果。在烘干房室内温度场趋于稳定后，取后20 min内（即第600 s~1800 s内）的测点数据，取每个测点在这20 min内的平均温度T，再计算20个测点的平均温度和风速的平均值和均方根偏差，求取不均匀系数。

表4 风口位置优化工况参数表

将25种工况分为五组进行对比，由图8可观察工况1~5、工况11~15、工况16~20这三组工况的平均温度和不均匀系数趋势图，可看出当1=2.535 m、1=2.8 m、1=3.8 m时，在指定范围内，送风口2离入口处距离越远，即2的值越大，在车栏杆处选取的测点的不均匀系数越小，而平均温度T的值越来越大，趋势呈相反状态；将工况6~9进行对比，当1=1.8 m时，2在10.45~12.65范围内，不均匀系数逐渐减小，平均温度也大致呈下降趋势；对比工况20~25平均温度和不均匀系数，可看出当1=4.8时，随着送风口中轴线2的值越大，不均匀系数先增大后减小，而平均温度的值先增大，再减小而后增大，并且这组工况的不均匀系数与其他组相比都偏大，说明测点温差较大，因此送风口1的位置最好设置在车尾后，这样车身温度更为均匀。

由图8可见工况4、工况5、工况12、工况14、工况15不均匀系数与工况3（原模拟结果）相比较低，工况2、工况13与工况3的不均匀系数较为接近，并且它们的平均温度都较为接近。在烘干房运行后二十分钟内，室内气流组织稳定时每层测点的平均温度T和不均匀系数情况如图9所示，工况1~10的一层温度不均匀系数最大，三层不均匀系数最小；工况1~4的一层平均温度最高，二、三层平均温度较为接近；工况11~15的一层和二层的不均匀系数较为接近，且一层、二层和三层的平均温度也较为接近；工况16~25的一至三层平均温度差距较大，三层平均温度最高，且工况20平均测点温度差约为2.3 ℃。工况1~5、工况11~14每层的平均温度最接近，且不均匀系数较低。

图 9 不同方案下测点的平均温度与不均匀系数

图 10 不同方案下每层的平均温度与不均匀系数

图 11 不同区域的平均温度与不均匀系数

由图10分析不同工况下左侧栏杆、中间栏杆和右侧栏杆的平均温度和不均匀系数，左、中、右栏杆处的平均温度曲线较为稳定，各工况间的平均温度值相差不大；工况1~15的不均匀系数较低，其中1~5、工况11~15的右侧不均匀系数最低，工况6和工况11~15的中间不均匀系数最低，工况2~4和工况12~14的左侧不均匀系数最低。

结合图8、图9、图10，分析得工况12、工况13、工况14的测点平均温度更为接近，不均匀系数最小，室内工作区温度场更均匀。分析这三种工况下的升温时间，工况14升到70 ℃时所需时间最短，因此，最佳优化方案1=2.8 m，2=12.65 m时室内温度场更为均匀，温升时间更短。

4.2 风口风速的优化分析

在运猪车厢内每层均匀选取6个测点，共计18个测点，研究在风口位置不变的情况下，风速变化对室内温度场及温升时间的影响。送风口1和送风口2的风速1、2分别取4 m/s、4.5 m/s、5 m/s进行对比分析。

表 5 风口速度工况参数表

由图11知，随着送风口1和送风口2风速的增大，室内整体平均温度也在增大，不均匀系数逐渐减小，第三层的温度不均匀系数最小。

工况1~3中，平均温度：第三层>第二层>第一层，不均匀系数：第一层>第二层>第三层；工况4~9中，平均温度：第一层>第二层>第三层，不均匀系数：第二层>第一层>第三层。由图12知，随着风速的增大，每层之间的平均温度差也在不断增大。工况1~6每层之间的平均温差较小，其中工况3、工况6的第三层不均匀系数最小，工况6的第一、二层的不均匀系数最小。

图 12 不同方案下测点的平均温度和不均匀系数

图 13 不同方案下每层的平均温度与不均匀系数

图 14 不同区域的平均温度与不均匀系数

将运猪汽车的车厢分为左右两个工作区，对比左、右区域的平均温度和不均匀系数，如图13。其中工况7、8、9的左右两区域的不均匀系数相差较大，因此综合比较分析，工况6的平均温度既满足条件，每层不均匀系数、左右不均匀系数又相对较小，相对温差较小。

5 结论

本文通过Airpak数值模拟软件研究单侧供热运猪汽车烘干房的气流组织特征，探究了烘干房送风口1和送风口2的不同位置处、不同送风速度下温度与速度的分布规律，得到1=2.8 m，2=12.65 m处的位置，烘干房内温度不均匀系数最小；送风速度1=4.5 m/s，2=5 m/s时，在最佳工况下，各测点的温度均满足烘干房的烘干要求，稳定后平均温度在78℃左右。

1）送风口2的位置越靠近车头位置，车厢前挡板处的温度就越高。送风口1的位置在后置风机和车尾之间（1=1.8~4 m）温度更均匀。

2）对车笼来讲，层高越高，平均温度越大，不均匀系数越小，测点最大温差越小。

3）靠近送风口侧的左侧栏杆不均匀系数>中间栏杆不均匀系数>右侧栏杆不均匀系数。

4）送风口1的位置在后置风机和车尾之间温度更均匀，其中轴线最佳位置1=2.8 m左右。

5）运行期间，送风口速度越高，平均温度越高，总不均匀系数越小，但每层车笼的温差越大，左右区域的不均匀系数值差越大。

利用烘干房的热风烘干运猪车辆，使用智能化系统操作简便，温度和风速可以进行智能调控，室内热空气分布均匀，车辆干燥后即可直接投入下次使用，相比自然晾干车身的水分所需的时间大大减少。运猪汽车烘干房后续需要不断地探索改进，优化其结构，以适应市场的发展需求。

[1]李玉杰,王庆伟,陈志飞.现代规模化猪场生物安全体系的规划建设[J].养猪,2018(6):73-76

[2]郝晓芳,徐佳,刘玲,等.从生物安全管理角度谈规模猪场对非洲猪瘟的防控[J].黑龙江畜牧兽医,2018(24):83-85

[3]张建虹.由非洲猪瘟引发的对设立跨省运输动物车辆准入制度的思考[J].当代畜牧,2018(14):5-6

[4]张宁宁,韩熹,李硕,等.运输车辆洗消中心建设和管理模式探讨[J].中国动物检疫,2019,36(12):33-35,44

[5]李传宗.大型汽车烘干房气流组织的数值模拟及优化研究[D].郑州:郑州大学,2017

[6]肖方恰.运猪汽车烘干房的气流组织试验及数值模拟研究[D].郑州:郑州大学,2018

[7]方雨彬.针对非洲猪瘟病毒的特点预防非洲猪瘟[J].养猪,2019(6):115-116

[8]刘泽勤,徐静,高行恭,等.送风高度对果蔬冷藏库内热环境的数值模拟研究[J].低温与超导,2019,47(12):72-77

[9]林涛,刘天力,黄鹏,等.高效节能烘干室的模拟仿真与设计[J].工业炉,2016,38(6):9-12

[10]周鑫涛,王博,申高展,等.深海载人平台密闭舱室气流组织数值模拟[J].船舶工程,2019,41(3):102-106

[11]陈豪,郭磊,华呈新.船舶舱室置换通风系统的数值模拟和优化[J].船舶,2019(4):1-6

Study on Numerical Simulation for Airflow Distribution in Automotive Baking Room with a Single Side Heating

LI Hui-zhi1, HOU Meng-yan1, XING Jin-chao2

1.450001,2.450001,

A new type of large pig truck drying room with one-side heating was used as the research object. By combining field measurement and Airpak numerical simulation, the air distribution of the drying room was studied, and the influence of different air inlet location and air supply velocity on the temperature field and drying quality of the drying room was analyzed.The study shows that when the positions of air inlet 1 and 2 are1=2.8 m and2=12.65 m, respectively, and the air inlet velocity1=4.5 m/s and2=5 m/s, the temperature non-uniformity coefficient in the drying room is the smallest, the temperature rise time is the shortest, and the air distribution is the best. On this basis, the characteristics of temperature and velocity distribution are analyzed to provide references for subsequent studies.

Automotive; baking room; air distribution; numerical simulation

TU834.3+3

A

1000-2324(2021)01-0084-07

10.3969/j.issn.1000-2324.2021.01.015

2019-01-12

2019-02-11

李会知(1965-),男,博士,教授,主要从事于建筑环境控制研究. E-mail:Lhz6380@zzu.edu.cn

网络首发:http://www.cnki.net