周期边界Korteweg-de Vries方程的高精度差分格式

程 宏

（闽南师范大学数学与统计学院，福建漳州363000）

Korteweg-de Vries(KdV)方程是一种单向运动浅水波偏微分方程，最早由Boussinesq 在1870年提出[1].KdV 方程在研究浅水中小振幅长波运动以及描述弱非线性回复力的浅水波现象中具有重要作用[2].同时，KdV 方程也广泛应用于磁流体波、离子声波、弹性棒中的纵色散波等方面.当前，对KdV 方程的数值方法的研究主要有有限差分法、有限元方法、拟(谱)方法及保结构算法等[3-5].

本文考虑如下一类周期边界KdV方程的初边值问题：

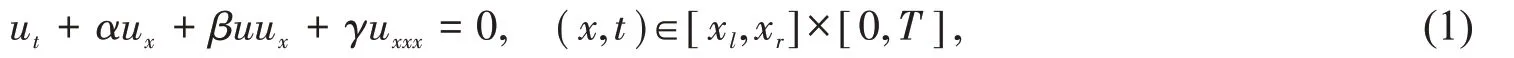
初值条件和边界条件分别为

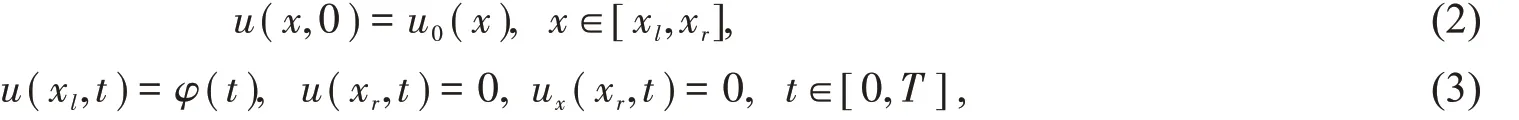
其中φ(t)为周期函数，α，β，γ为非负常数，u0(x)为已知函数.当α=0 时，方程(1)即为经典的KdV 方程.实验室水流模拟结果表明[6]，当边界条件中φ(t)为时间周期边界时，浅水波的流动也具有周期性，且保持了与边界相同的周期，这就促使我们寻找一个精确的数值方法，来验证在此条件下浅水波流动的周期性.

1 高精度差分格式

我们考虑建立KdV 方程(1)-(3)的三层线性四阶精度差分格式.首先，构造如下网格：xj=xl+jh,tn=nτ, 0≤j≤J, 0 ≤n≤N,其中h=(xr−xl)/J和τ=T/N分别为空间和时间方向上的步长.设unj为u(xj,tn)的近似解，即unj≈u(xj,tn).为方便计，引入如下记号：

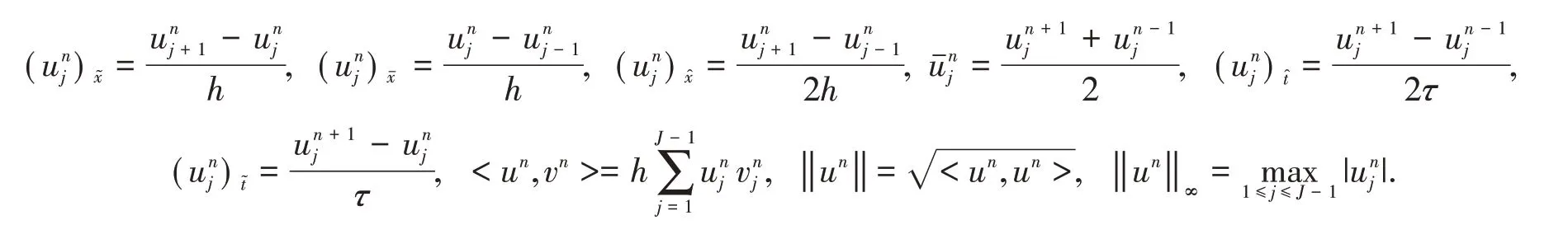
令w=−αux−βuux−γuxxx,则式(1)可写为w=ut.对式(1)两边同时对变量x求二阶导数，则有

同时，利用泰勒展开得到

对于三阶导数的离散，我们采用如下四阶离散格式[7]

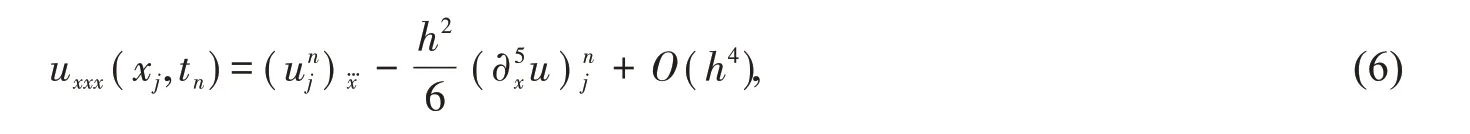
这里

由式(4)-(6)，我们可得

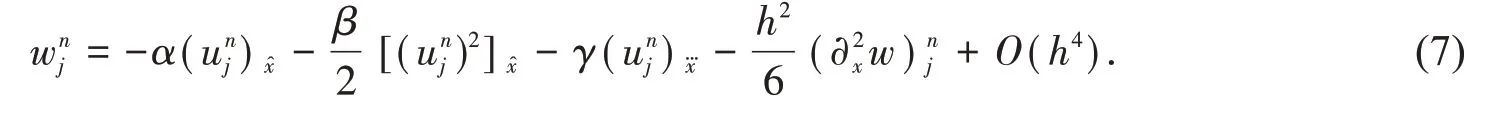
同时，我们有

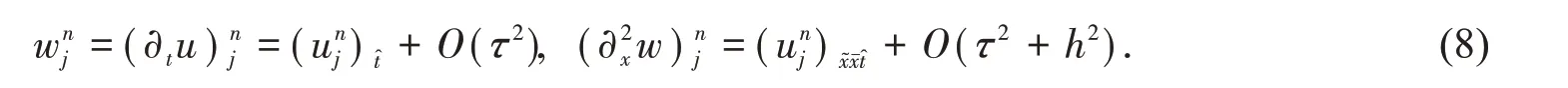
由式(7)-(8)，我们对式(1)-(3)建立如下高精度差分格式：

由于式(9)在时间方向上是三层格式，在具体运算的时候，还需要知道u1的值.为此，考虑如下两层时间格式：

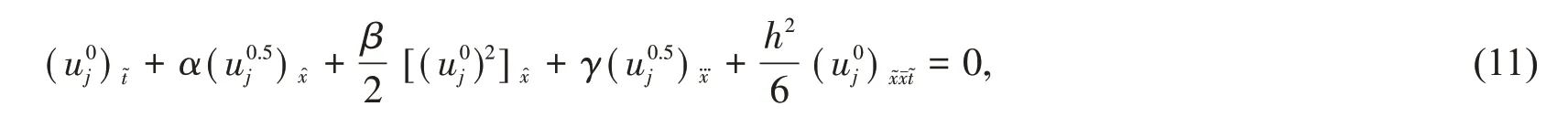
其中1 ≤j≤J−1.可以看到，式(11)同样在时间方向上是二阶精度，在空间方向上是四阶精度.

2 收敛性和稳定性分析

为证明式(9)-(11)的收敛性和稳定性，我们只考虑齐次方程零边界的情况，即φ(t)= 0，且记

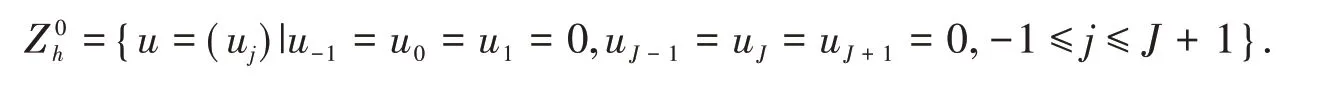
引理1[8-9]任取两个函数u,v∈Zh0，则有

引理2[7]任取函数u∈Zh0，则有＜u…x,u＞= 0.

引理3任取函数u∈Zh0，则有

证明由于u∈Z0h，有

引理4[10]任取函数u∈Z0h，存在不依赖h的常数C＞0，使得

定理1假定u0(x)∈H20(Ω)，则式(9)-(11)的解满足进一步有

证明利用数学归纳法证明.由式(10)可得第一层u1的值可由式(11)计算，可得假定式(9)两端对做内积，由引理1得

由柯西-施瓦兹不等式[8]及引理2得

定理2若u0(x)∈H20(Ω)，则差分格式(9)-(11)的解是唯一的.

证明用数学归纳法证明，由于u0和u1分别可由初始条件(10)和两层格式(11)唯一确定，假设u1，u2，…，un是唯一可解的，考虑式(9)的齐次方程形式：

式(14)与un+1做内积，由引理1，2，3 得从而因此，式(14)存在唯一的零解，故而式(9)-(11)存在唯一的解.

定理3若u0(x)∈H20(Ω)，则差分格式(9)-(11)的解收敛到式(1)-(3)的解，且收敛阶为O(τ2+h4).

证明令这里和分别表示初边值问题式(1)-(3)的精确解和式(9)-(11)的数值解，则误差方程为

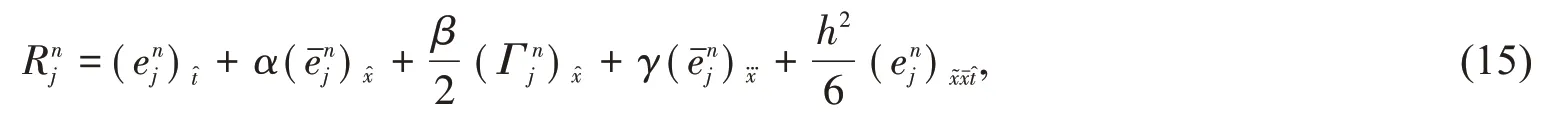
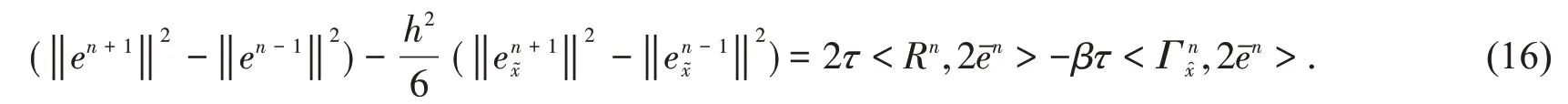
由引理1和定理1可得

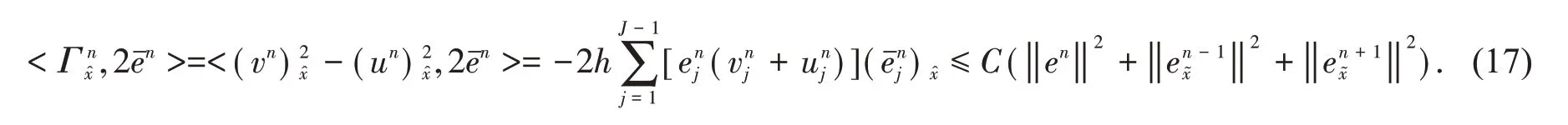
同时，由柯西-施瓦兹不等式得

将式(17)-(18)代入式(16)中得

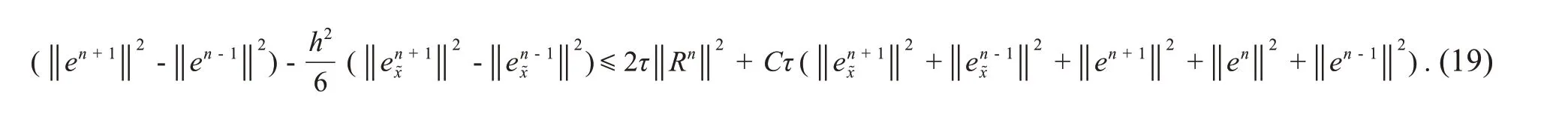
由式(11)得e0=0,Λ1=O(τ2+h4)2, 则由离散Gronwall不等式[11-12]得Λn≤O(τ2+h4)2，即由引理4 可得从而可知式(9)-(11)的解以‖⋅‖和‖⋅‖∞范数收敛到式(1)-(3)的解，收敛阶为O(τ2+h4).

类似于定理3的证明过程，可得定理4：

定理4若u0(x)∈H02(Ω)，则式(9)-(11)的解以‖⋅‖和‖⋅‖∞范数稳定.

3 数值实验

例1在KdV方程中取如下参数(α=0,β=1,γ=1,φ(t)= 0)，可得如下方程[13]：

初值条件为

该问题的解析解为

在本算例中，我们选取如下参数：κ=0.3,x0=0,Ω =[−30,30], 表1给出T=10,h=1.0,τ=0.5 时误差和收敛阶，这里收敛阶为[15]

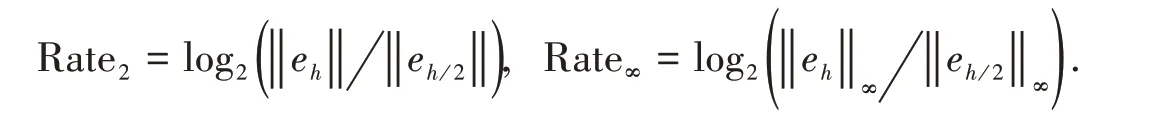
从表1可以看出，本文格式精度接近于理论分析的四阶精度，这就验证了理论分析的正确性.

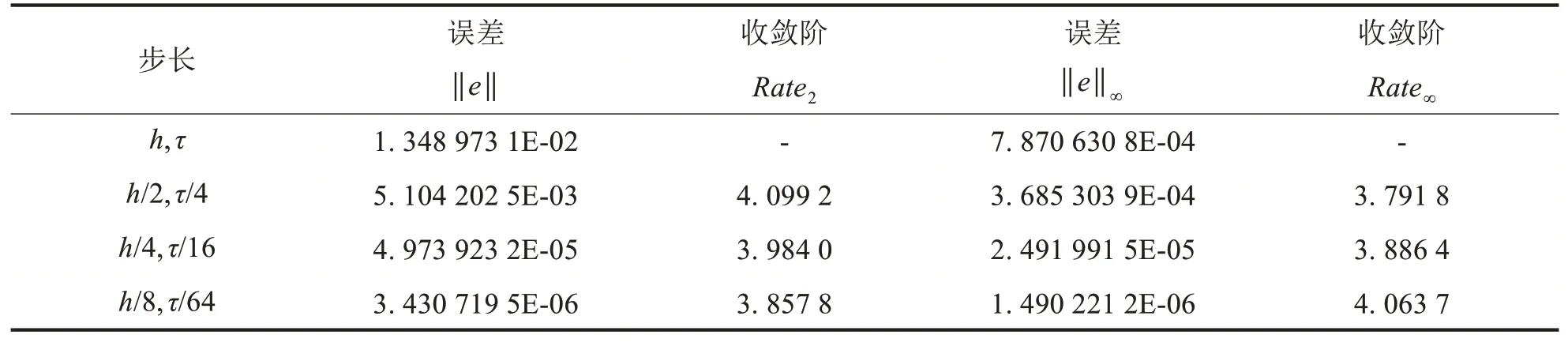
表1 误差和收敛阶Tab.1 Error and convergence rate

为了和其他格式比较，式(20)的如下守恒量[14，16-17]：

表2中列出了h=1.0,τ=0.5,T=10时本文格式、Sinc方法[14]和Lines方法[16]计算这些守恒量的误差值比较.从表2中可以看出，本文方法计算结果比Sinc方法[14]和Lines方法[16]都要精确.

表2不同守恒量误差值的比较Tab.2 Comparison of errors of different conserved quantities

例2在KdV方程中取如下参数(α=1,β=2,γ=3)，可得如下方程[14]：

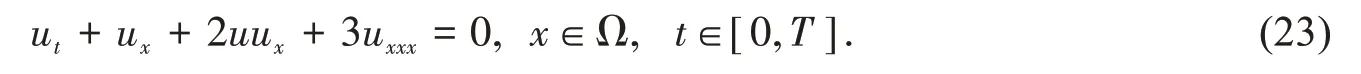
此问题的初值可取式(21)，但其精确解是不知道的.

本算例我们取如下参数：x∈[0,1],h=0.01,T=1,τ=0.001,κ=0.5,x0=5.图1中分别给出边界条件φ(t)= sin(5πt)和sin(10πt)时三维波的传播图形.从图1可以看出，波的传播具有周期性，且周期与边界条件中的函数φ(t)的周期性相同，这就验证了我们最初的猜想是正确的.

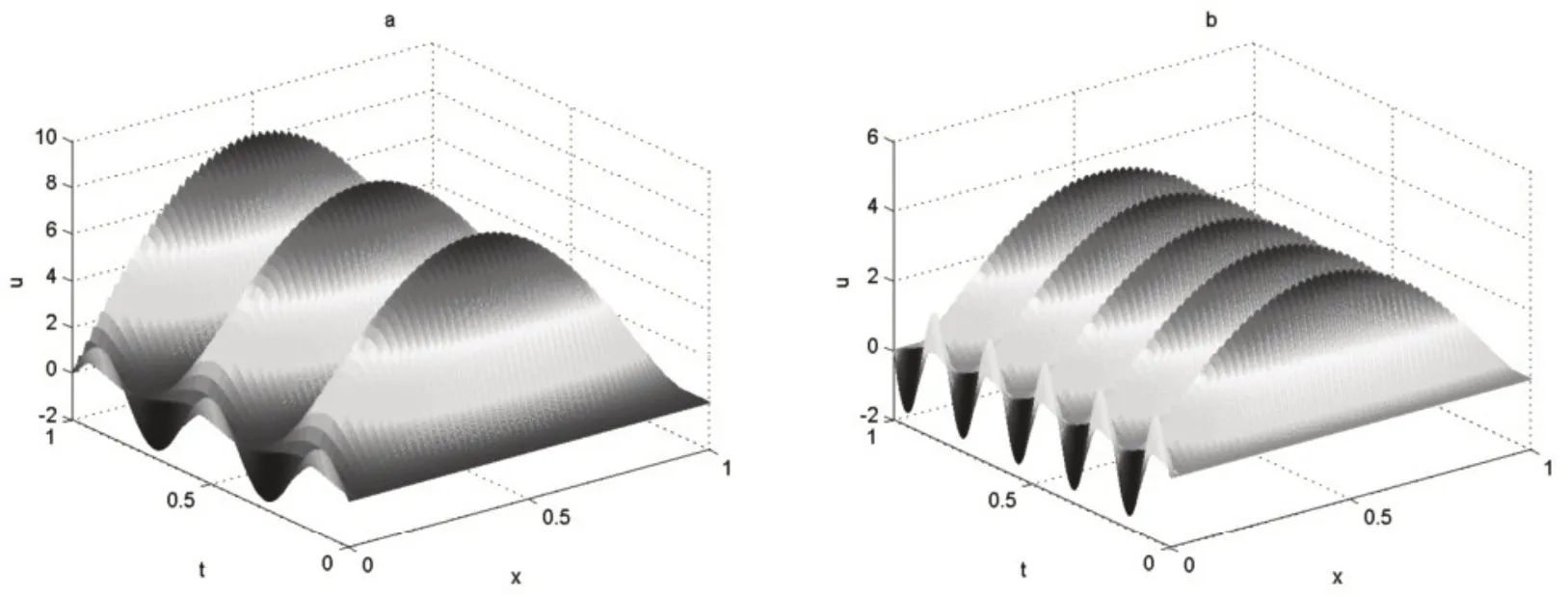
图1 波的传播周期解三维图形Fig.1 3D figure of periodic solutions for wave propagation

4 结语

本文主要是对周期边界的Korteweg-de Vries方程建立了三层线性高精度差分格式，格式的收敛阶为O(τ2+h4)，并严格证明了所构造数值格式解的存在唯一性、稳定性与收敛性，数值实例验证了数值解保持了与边界周期相同的周期性.