矩形截面高层建筑立面上面风压极值的尺度折减系数

全 涌，王 翔，张正维

（1.同济大学土木工程防灾国家重点实验室，上海，200092；2.奥雅纳工程咨询（上海）公司，上海，200031）

为了简化起见，工程设计中常常有人直接采用测点风压的最不利值进行围护结构设计，这默认受压面上不同位置处的风压时程是同步变化的。但实际情况并非如此，受压面上的风压在时间和空间上都是不断变化的，面积平均风压（下文简称“面风压”）极值将随受压面的增大而减小，这种效应一般用尺度折减系数或者尺度折减系数来表达［1］。

Marshall［2］对一栋单层住宅进行了风压现场实测和模型风洞试验，并对屋盖表面某些测点的风压时程进行加权平均处理来计算作用于较大面积上的极值风压，结果表明随着受压面的增大，极值风压显著减小；Davenport等［3］通过面积平均方法研究了风压极值随受压面增大而衰减的规律以及屋盖不同位置的尺度折减系数的变化规律；Lawson［4-5］针对围护结构尺度折减效应提出了移动平均法，并建议所给公式中的参数K取4.5；Stathopoulos等［6］采用气动总管方法测量得到高层建筑围护结构风压系数随受压面积增加的减小的曲线；梁益［7］根据高层建筑表面密集布点的风压测量结果，认为极值负压下Lawson［5］公式K值为3.7，极值正压下K值为2.2；Gavanski等［8］根据NIST数据库中的低矮建筑风压数据，用面积平均方法确定墙面的风压系数并与日本规范AIJ（2004）和美国规范ASCE7-10中随受压面面积变化的风压系数进行对比，发现AIJ规范高估了10 m2以上受压面上的极值负风压，而低估了其正极值风压；且ASCE7-10低估了几乎所有受力面积上的正极值风压；Hong［9］采用一种模块化的方法对测压模型进行密集布置测点，并且改变建筑高宽比，对比ASCE7-10规范，提出与Gavanski等［8］相似的结论。

一般认为尺度折减系数与受压面面积相关，但实际上可能还与受压面位置和形状有关，可在既有研究中受压面形状和最不利风向一般被忽视，这有可能导致给出的尺度折减系数不准确。本文基于刚性模型的风压测量风洞试验，研究了受压面的大小、形状和位置对面风压极值的尺度折减系数的影响。

1 风洞实验设置

考虑高层建筑多处于城市中心或大都市市郊，本研究采用C类地貌［10］，以一栋高度H为60 m，宽度B为30 m的方形截面高层建筑为例进行风洞试验研究。此外，相同模型尺寸下，大比例模型的单个测点代表的风压作用面积较小，使得面积平均方法所得到的面风压更加接近真值，故模型长度、风速和时间缩尺比分布为1/100、1/4和1/25。数据采集频率和长度为500 Hz和144 s，对应于足尺模型20 Hz和60 min。

风场模拟结果如图1所示，建筑高度处风速VH（量纲一），Iu为湍流度，10 cm高度处的来流试验风速为6.3 m·s-1，模型顶部高度处的紊流积分尺度为60 cm左右，分别对应于足尺模型10 cm高度处风速25.2 m·s-1和湍流积分尺度60 m。图1b为建筑高度处来流脉动风功率谱。

图1 C类地貌风场模拟结果Fig.1 Results of wind field simulation of category C

风洞试验模型采用模块化组合模型，标准模块利用光敏树脂材料通过3D打印技术制作而成，其他附属模块采用铝板制作；测点与扫描阀之间采用长800 mm、内径1 mm的PVC管连接。试验模型相邻管道壁厚为2 mm，测压管道3D打印部分的最长处仅5 mm，占管道总长不到1%，可保证数据可靠性。

模型详细信息如图2a所示，测压管道均匀地布置于测压模块表面，测点中心距统一为3.7 mm，对应于足尺0.37 m。同步测压的面积为三种不同高宽比的矩形，面积类型1、2和3的高宽比分别为1、1/4和4。本次测压范围为不受三维流影响的0.50～0.75高度范围。测压面迎风时定义为0°风向角（图2b）。试验风向角范围为0°～360°，风向间隔为10°，在0°，90°，180°，270°附近风向角梯度加密到5°。

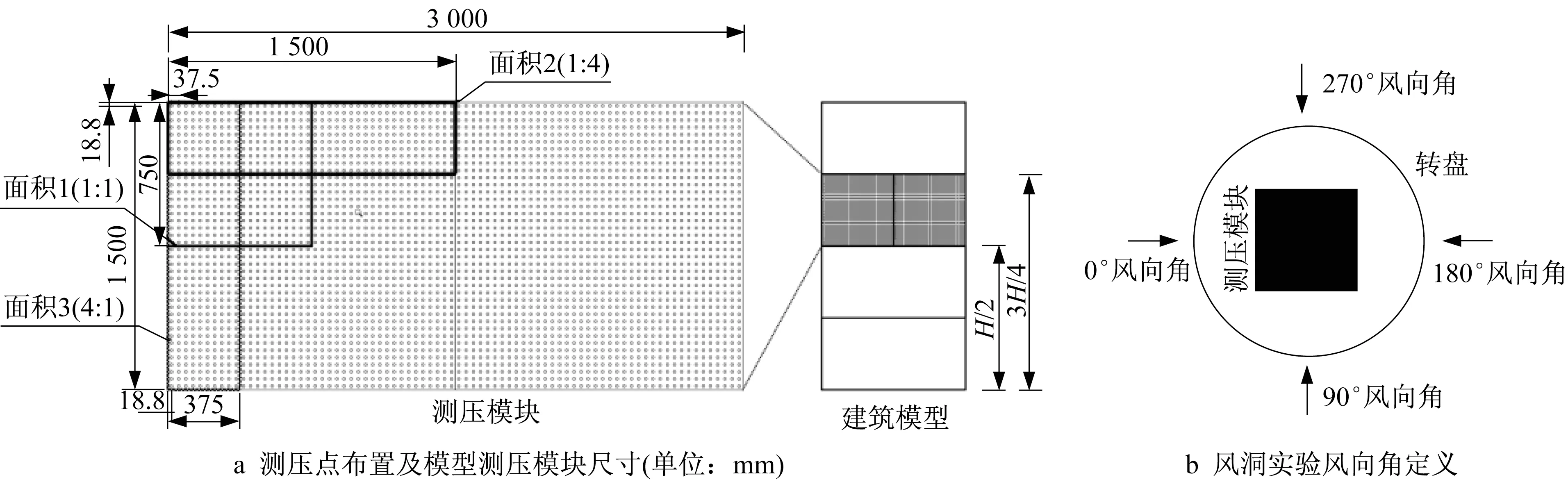
图2 测压点布置及模型测压模块尺寸及风洞实验风向角定义Fig.2 Arrangement of measurement taps and position of module and definition of wind direction

2 数据处理

面风压系数时程计算如下：

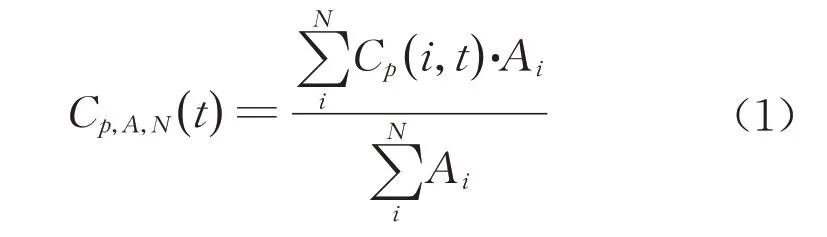
式中：Cp，A，N(t)和Cp(i，t)分别为包含N个测点的受力面积A面风压系数时程和测点i的点风压系数时程，其来流风压的参考高度为建筑高度；Ai为测点i所代表的风压作用面积。

极值风压系数利用全涌等［11］推荐的方法计算，但给出的值不是风压系数的极值期望值，而是Cook和Mayne［12］定义的极值风压系数（CM系数）。极值计算时观测时矩取10 min。

考虑面积最不利风向角下，两测点间的风压相关系数定义如下：

式中：rcor(i，j)为测点i与测点j上风压系数的相关系数；Cov(Cpi，Cpj)和Var(Cpi)分别为极值风压的互相关系数与自相关系数。

含有N个测点的受压面面风压极值的尺度折减系数CA，N的计算过程如图3所示。

3 试验结果

3.1 风压系数的空间相关性分析

3.1.1 水平相关性

选取最靠近建筑边缘的测点作为参考点，分析测点高度对最不利风向下建筑风压水平相关性的影响，分析结果如图4所示。随着两测点间水平距离的增加，风压的相关性快速地下降到0附近。对比图4a与4b可知，正负压作用下的空间相关性表现为不同的下降趋势。正压作用下的相关性曲线为先快速下降，下降速率随距离的增大逐渐减小并趋于平缓。负压作用下在距离小于建筑宽度10%时的相关系数下降速率相对较慢。在距离为10%～40%时下降速率相对较快，大于40%后下降速率又变慢。此外，无论极值正负压，测点高度z对水平相关性的影响不明显。但当测点接近建筑顶部或者底部时，因三维流的影响，测点间风压的相关性可能会有较大的不同，这些特别的区域不在本文研究范围，有待进一步关注。

图3 尺度折减系数计算流程Fig.3 Test data process of size reduction factor

3.1.2 竖向相关性

将建筑0.75 H位置处的测点作为参考测点，选择建筑0.75 H～0.50 H之间的测点分析竖向测点间的相关性。图5展示了在距建筑边缘0.125 B范围内，测点距建筑边缘的距离x'对竖向相关性的影响。随着测点间距离的增加，竖向的相关性呈下降趋势，并且相关性曲线近似线性。正压极值的竖向相关性在测点间距达到0.50 B时下降到0.7～0.8范围附近，而负压下相同距离下降较快达到0.55～0.60范围附近。同一竖列的测点间最不利正风压（迎风面）的相关性随测点列距建筑边缘的距离的增大呈增大趋势。如图5a所示，建筑边缘2.5%的距离处测点列与距边缘12.5%处测点列的正压相关性最大相差为0.11。然而，这样的现象在最不利负风压（侧风面上）上表现并不明显，侧风面最不利负风压的相关性曲线距边缘不同位置最大差异仅为0.05，如图5b所示。

图5 测点距建筑边缘的距离对风压竖向相关性的影响Fig.5 Influence of distance between taps and edge of facade on vertical correlation of wind pressure

图6比较了水平和竖直两个方向上极值风压系数的空间相关性。在测点间距相同时，无论正风压还是负风压，竖向相关性明显都高于水平相关性，且极值正风压的水平、竖直关性差异较极值负压明显。

3.2 受压面面积对面风压极值尺度折减系数的影响

图7给出了建筑0.75 H～0.5 H之间，受压面为方形（面积类型1）时其面积从0.14～50 m2的变化过程中尺度折减系数的变化。图中明显展示了当附属面积在建筑立面的位置变化时，正负风压极值的尺度折减系数都在一定的范围内变化，平均尺度折减系数随受压面积的增加呈下降趋势，面风压正极值尺度折减系数从在0.14 m2接近1，50m2时为0.89左右，面风压负极值折减系数从1附近折减到0.80。图7中也对比了本文研究结果与梁益［7］、Hong［9］研究以及我国建筑荷载规范GB 50009—2012［10］中的尺度折减系数。结果展示出已有研究结果与本文研究较为相似，但由于建筑体量和来流风场湍流度差异导致折减曲线存在细微差别。值得注意的是我国的建筑荷载规范中规定的尺度折减系数明显小于各个研究中的结果，尤其面风压正极值的折减系数明显偏小。

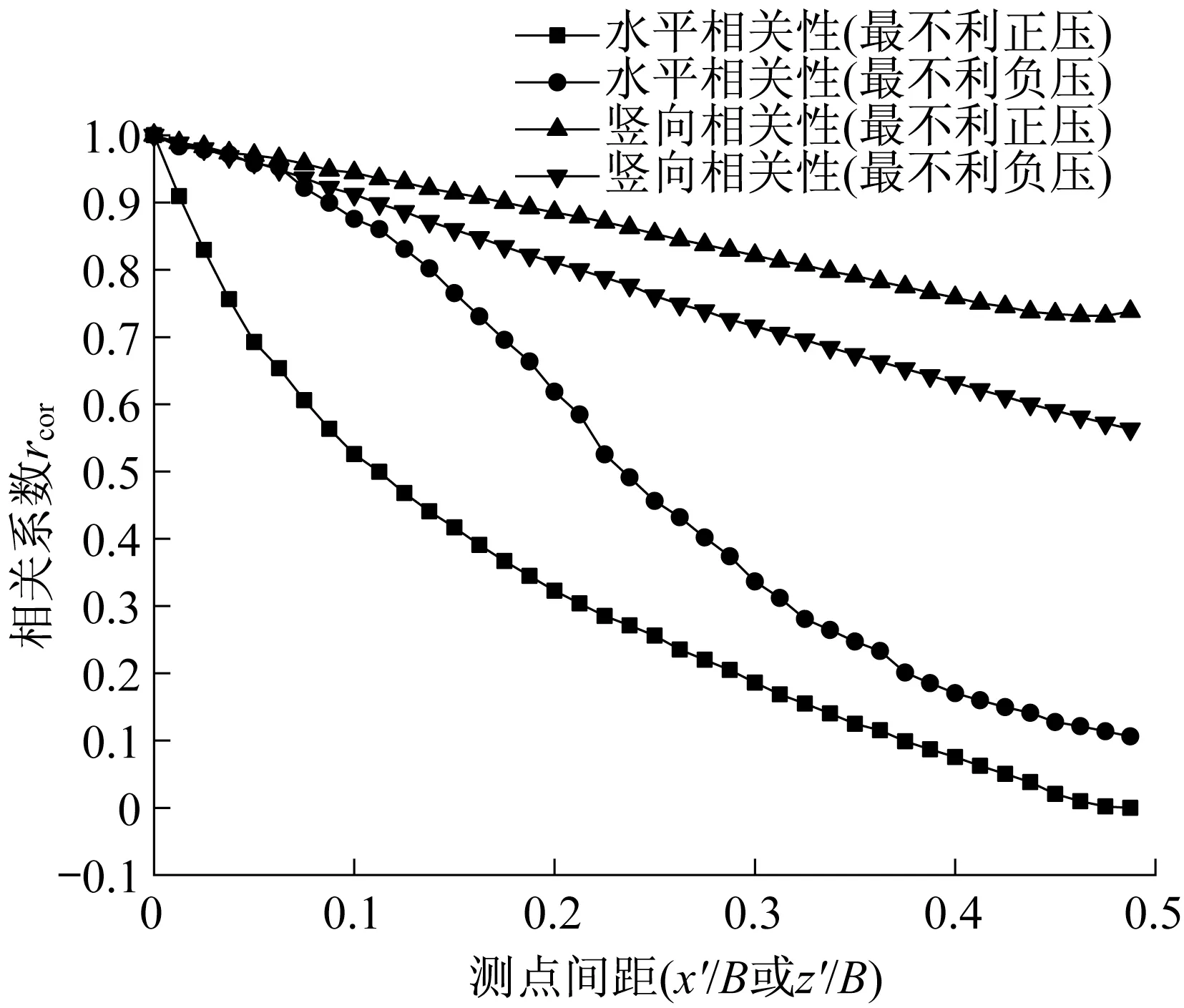
图6极值风压的横竖相关性对比Fig.6 Comparison of two-direction correlation in most unfavorable positive and negative wind pressure

3.3 风压极值尺度折减系数的尺度参数选择

由3.1节分析可知，围护结构上各测点风压表现为水平相关性小而竖直相关性大，这一特点表明围护结构面风压极值受其水平尺度影响大而受竖向尺度的影响小，但通常研究者将受压面面积作为尺度参数来研究面风压极值的尺度折减系数，而不是分开考虑水平尺度和竖向尺度。如3.2节所示，对于相同的受压面面积，面风压系数极值的尺度折减系数并不相同，且具有较大的离散性，可见以受压面面积作为尺度参数来考查面风压极值的变化并不合适。如图8a所示，对于相同的受压面面积，受压面高宽比对尺度折减系数有明显的影响，高宽比越大折减系数越大。

有的研究者［5］将受压面的最大尺度（如矩形的对角线）定义为特征尺度，作为尺度参数考查尺度折减系数。图8b展示了将对角线作为尺度参数时高宽比对折减系数的影响。虽然未能将不同高宽比受压面的折减系数统一起来，但比面积作为尺度参数时的规律性好一些。

考虑到受压面宽度b对测点风压间的相关性影响较大，这里也将它作为尺度参数考查折减系数变化趋势，结果如图8c所示。不同高宽比受力面的折减曲线进一步聚集，但仍然有较大的离散性。从3.1分析可知，受压面的水平尺度b和竖向尺度h都对测点间的风压相关性有影响，b的影响大，h的影响小。同时，建筑的迎风面宽度B对特征湍流的湍流积分尺度有重大影响。基于以上两点考虑，本文以综合参数为尺度参数来描述面风压极值的尺度折减系数，其中α为拟合参数。经拟合，α=0.85，即综合尺度参数取b0.85h0.15/B。此时，不同高宽比的矩形受压面的尺寸折减系数基本聚在统一的曲线上，离散性最小，如图9所示。

图7极值风压的尺度折减系数Fig.7 Reduction coefficient of extreme area-averaging wind pressure

图9中粗实线为拟合得到的尺度折减曲线，其中最不利正风压（图9a）为

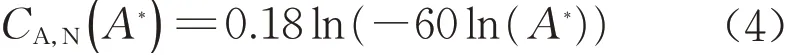
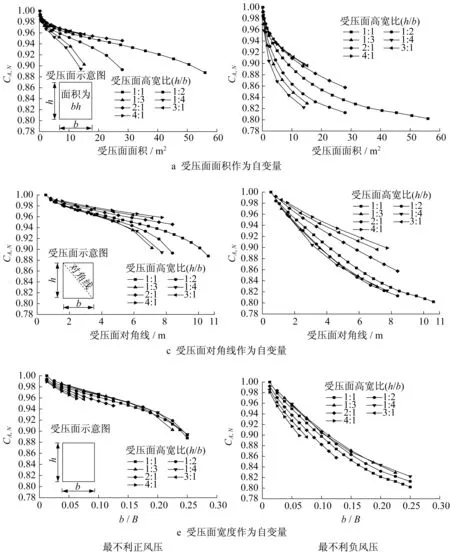
图8受压面的不同特征尺度作为自变量对其折减系数的影响Fig.8 Effects of different characteristic parameters as independent variable on size reduction factor of forced areas

图9 综合尺度参数（b0.85h0.15/B）对CA，N的影响Fig.9 Comprehensive parameter(b0.85h0.15/B)versus CA,N

4 结论

本文通过一系列刚性模型测压风洞试验，讨论了矩形截面高层建筑中段（不受顶部和底部三维流影响的高度范围）立面幕墙上测点风压极值的相关性和面风压极值尺度折减系数的变化特征，得出结论如下：

（1）测点风压的水平和竖向相关性受参考点高度（不受顶部和底部三维流影响的高度范围）影响不明显，参考点到立面边缘的距离对相关性有明显影响。在相同距离下，无论面风压的正值极值还是负极值，竖向相关性明显大于水平相关性，且面风压正极值的竖向相关性与水平相关性的差异较负极值的明显。

（2）当受压面在建筑围护结构上不同位置移动时，面风压极值的尺度折减系数表现为一定范围变化，其均值随受压面面积的增大而减小；对比本文研究结果、已发表文献研究结果及我国建筑荷载规范GB 50009—2012中尺度折减系数规定发现，在极值风压作用下，我国建筑荷载规范中的尺度折减系数偏小，在极值正风压作用区域这种差异尤为明显。

（3）综合尺度参数A*（b0.85h0.15/B）作为尺度折减系数曲线的自变量时，不同高宽比受压面上面风压极值的尺度折减系数将聚集在一条曲线上，离散性很小，并拟合出此参数作为自变量的折减曲线。

作者贡献声明：

全涌：确定具体研究内容和实施方案，指导论文撰写及修改成稿；

王翔：完成试验设计及实施，数据分析，撰写论文初稿；

张正维：提出研究目标，协助指导试验设计。