考虑驾驶员模糊感知的深度学习跟驰模型
2021-04-01李林波李瑞杰邹亚杰
李林波,李瑞杰,邹亚杰
(同济大学道路与交通工程教育部重点实验室,上海201804)
跟驰模型的研究对交通安全及通行效率有很大意义。从建模方法角度划分,跟驰模型可分为理论驱动与数据驱动两类[1]。理论驱动类模型按照不同的建模机理,可以进一步分为刺激反应类[2]、安全距离类[3]、心理-生理类[4]、优化速度类[5]、基于期望值的模型[6]等,其优点是可以描述跟驰过程中的某几个显性因素,但对驾驶人的驾驶经验以及模糊感知特性,难以准确刻画。基于此,Yu[7-8]先后将车头间距、相对速度作为驾驶记忆,并改进全速度差模型,得出考虑驾驶记忆可以提高驾驶稳定性,并减少燃油消耗等;Sun[9]将一段时间内本车与前车速度差作为驾驶记忆,用来改进最优速度模型,通过控制论方法提高了驾驶的稳定性。Tang[10]基于最优速度模型,通过设计权重考虑了两个不同时刻的刺激,来模拟驾驶人记忆。由于这些方法只能考虑很少的记忆时刻,同时仅考虑了一个影响因素作为驾驶记忆,当公式变得复杂时,反而会失去理论模型的简洁性。模糊控制类方法[11-12]需要根据人为经验构建模糊控制规则、选取隶属度函数等,从而对数据造成了主观干预。随着大数据技术、人工智能及深度学习的迅速发展,从数据驱动的角度,基于人工神经网络方法,直接对数据样本进行学习并预测,被证明能够更为准确地模拟人的行为特性。Panwai[13]最先构建了简单的反向传播神经网络,基于车上传感器采集的数据对模型进行训练,仿真结果比基于Gipps的模型结果有更高精度,说明了基于神经网络方法在跟驰行为预测上的适用性。Wang等[14]较早验证循环神经网络方法比传统跟驰模型建模方法能大幅提高模型精度。随后不同学者通过神经网络类方法研究驾驶员各种特性,如捕捉驾驶员非对称驾驶行为[15],驾驶记忆影响[16-17],驾驶员的反应延迟现象[18]等。然而,基于数据驱动的跟驰模型在数据获取方式和精度方面依然存在一定的不足,当前用于训练神经网络的跟驰数据获取方式主要分为:①在车上安装各类传感器,获取前车与本车位置、速度以及间距等数据;②通过驾驶模拟器获取相应数据;③通过摄像机在高处对某路段进行视频录制,并随后通过视频图像处理技术,提取视频中车辆原始轨迹数据。
车载传感器方式可能会对驾驶员以及道路周边用户行为造成影响,导致收集的数据无法准确反映自然驾驶行为,而通过高空安装摄像头或无人机航拍获取路段视频数据,并通过图像处理技术得到路段监控区域所有车辆轨迹信息可以避免对交通参与者的干扰,基于该方法使用最广泛的数据为下一代仿真(next generation simulation,NGSIM)数据。为排除数据中固有误差,许多文献[19-20]进行了各种预处理。然而NGSIM数据集存在许多相邻轨迹间重合、速度-加速度矛盾,低分辨率带来的车辆位置标识误差等问题,且无法严格清洗或插补数据[21]。由于基于深度学习类的人工智能算法,直接通过各种类型跟驰数据进行学习,因此,数据来源的缺陷必然会对预测结果产生不良影响。
由于人工驾驶常无法精准感知当前时段的本车速度、车头时距等跟驰状态,在行驶过程中,需要依靠之前的驾驶记忆,并对即将出现的跟驰场景不断进行预估,从而进行相应操作,而预估的驾驶场景,通常都是不确定的,与实际有一定的差别。这一特性可解释,即使相同的驾驶员,在相同的跟驰场景下,每次的操作都不会完全相同。因此,本文同时将本车速度、与前车车速差、车头间距作为驾驶记忆,基于门控循环单元(gated recurrent units,GRU)/长短期记忆网络(long short-term memory,LSTM)循环神经网络,提取highD数据集中的跟驰片段,采用端到端的方式训练模型,减少主观因素干扰。在模型输入端,设计了模糊感知时间窗,将模型计算出的部分预测值,与序列中的本车真实状态值进行替换,来模拟驾驶人对跟驰场景的模糊感知特性,对不同仿真场景以及不同模糊感知时间窗下跟驰场景进行实验,验证不同模糊感知时间窗下的不同跟驰行为。该方法可快速生成大量异质跟驰行为,有利于进一步仿真研究走走停停、震荡、交通流失效、迟滞回环等现象的发生。
1 数据分析
1.1 数据说明
highD数据集是2017年9月份在德国公路上,通过高空无人机航拍后,并依次使用先进的计算机视觉算法、神经网络及贝叶斯平滑算法提取出的自然驾驶轨迹数据集,提取出的轨迹数据每秒25帧,其定位误差通常小于10 cm[22]。关于数据的具体描述见文献[23],被提取出的数据集被分为60份,每份包含4个文件,分别为高速公路特定区域的高空照片,以及关于地点元数据、轨迹元数据、每车每帧轨迹的详细信息。数据集中包含德国6处不同高速公路路段。本文基于路段2的车辆轨迹数据进行跟驰行为研究,经统计,路段2轨迹数据包含2 400辆小汽车,674辆卡车。如图1所示,车辆分布于4个车道,LaneID为车道标识,图中分别为2、3以及4、5车道。2、3车道的车辆向左行驶,4、5车道车辆向右行驶。需注意的是,由于highD数据集使用了全球坐标系,且原点在图像左上角,横、纵坐标轴左边分别向右、向下。因此,原始轨迹数据中2、3车道行驶的车辆速度记录为负值,加速度为负值代表加速。

图1 路段2示意图Fig.1 Diagram of road segment 2
1.2 跟驰行为提取准则
highD数据集中包含小汽车以及卡车两种类型轨迹数据。由于不同车型跟驰行为有很大差异,本文针对小汽车的跟驰行为进行筛选。由于highD轨迹元数据中的numLaneChanges字段表示车辆换道次数,因此,可通过该字段进一步删除存在换道行为的车辆轨迹数据。筛选跟驰片段持续15 s及以上的轨迹数据,也即每个跟驰片段至少包含375帧。经上述处理后,得到的数据集共94条跟驰片段,总时间为4 895 s。
2 模型建立
2.1 LSTM块及GRU块结构
跟驰片段数据集是较为典型的时序数据。目前,在跟驰行为预测上,广泛使用的循环神经网络有两种,分别为LSTM[7-8]及其一种结构更为简洁的变体GRU[6]。这两种模型在跟驰行为预测上,均有不错表现,但笔者却未发现,两种模型针对于同一数据集的对比分析,在此,不同单元结构也当作模型超参分析。LSTM的总体结构[24]如图2所示,xt为t时刻的输入向量,ht为t时刻输出向量,ht-1为t-1时刻输出向量,ct-1为t-1时刻输入的记忆单元,Ct为t时刻的输出记忆,c͂t为更新ct-1记忆单元的中间变量。LSTM通过遗忘门ft、输入门it以及输出门ot,将输入数据xt、输出数据ht、以及记忆单元ct结合起来,其中σ以及tan h分别代表sigmoid以及双曲正切激活函数,⊗代表向量间点积。
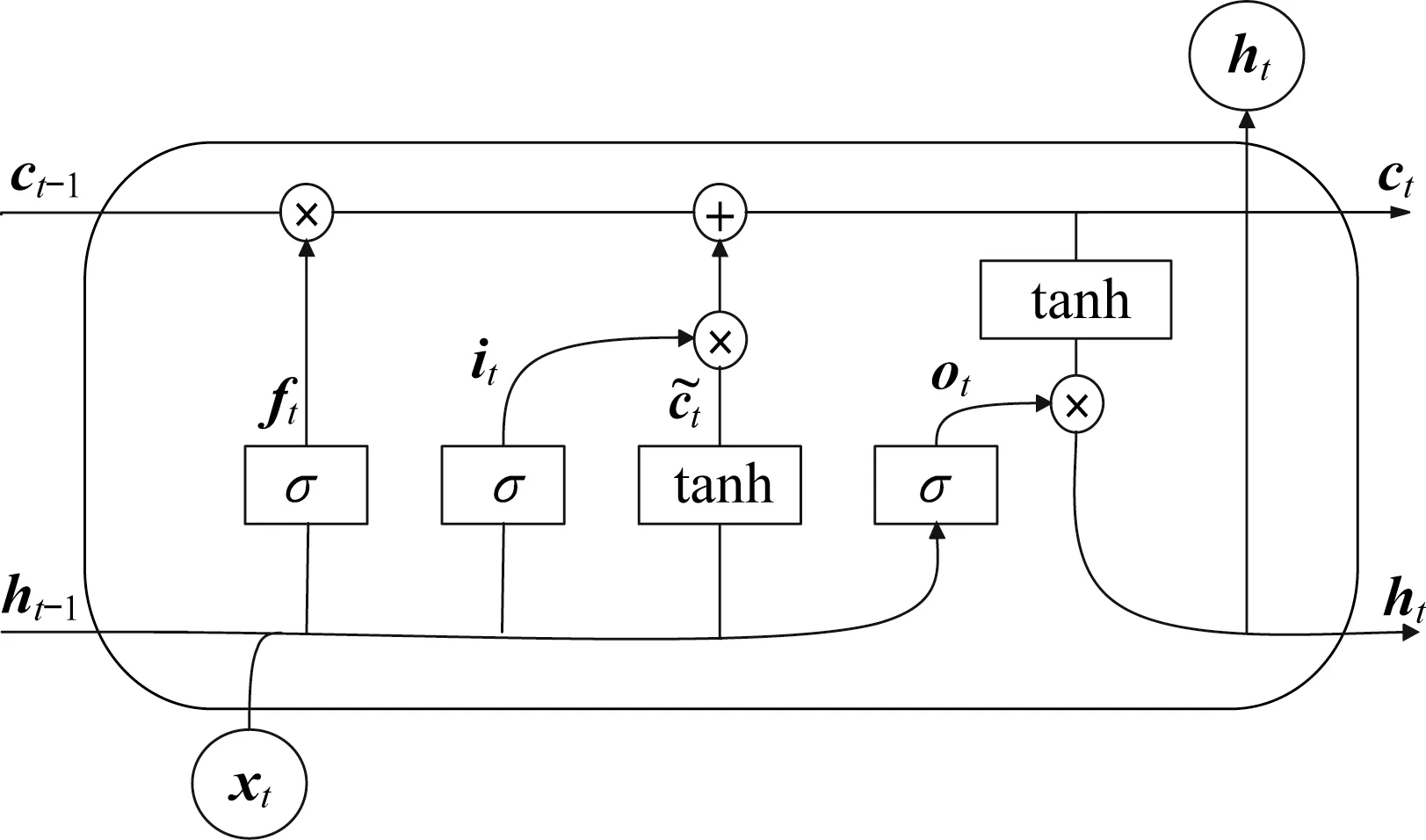
图2 LSTM单元结构Fig.2 Structure of LSTM unit



图3 GRU单元结构Fig.3 Structure of GRU unit

2.2 网络结构
在本车初始状态已知的情况下,在下一时刻,对于位移、速度、加速度三个状态变量,模型只需预测其中一个,就可根据牛顿运动定律,得出另外两个。模型损失函数以及评价指标常基于模型预测值进行构建。由于在稳定跟驰状态下,加速度接近于0,导致基于加速度构建的评价指标常常出现一些不必要麻烦,如无法加入权重、难以计算结果等。以评价指标平均相对误差绝对值为例,由于该指标分母包含加速度,当加速度趋于0,会导致式子趋于无穷大,无法准确描述模型精度[26]。如图4所示,基于GRU/LSTM的跟驰模型训练是将一段时间的特征序列作为输入,从而计算下一时刻的跟驰行为,其中cn,1代表第一层网络中第n个时刻的记忆单元,hn,1代表第一层网络中第n个时刻的输出,其他变量以此类推。本模型将连续n个时刻的:①本车速度vn;②本车与前车的相对速度Δvn;③本车与前车的车头间距sn作为输入特征,在经过多层GRU/LSTM隐藏层之后,通过一层Dense全连接层,将最后一个时刻的单元输出转换为一维数据,代表第n+1时刻的本车速度。与普通全连接层神经网络不同的是,由于LSTM/GRU块对时序数据的处理是自循环方式,无论输入的时间步长的长短,训练的模型参数都是固定的,因此,每一隐藏层的神经元个数,确切来说,是每层单个LSTM/GRU块的输出h的维度。
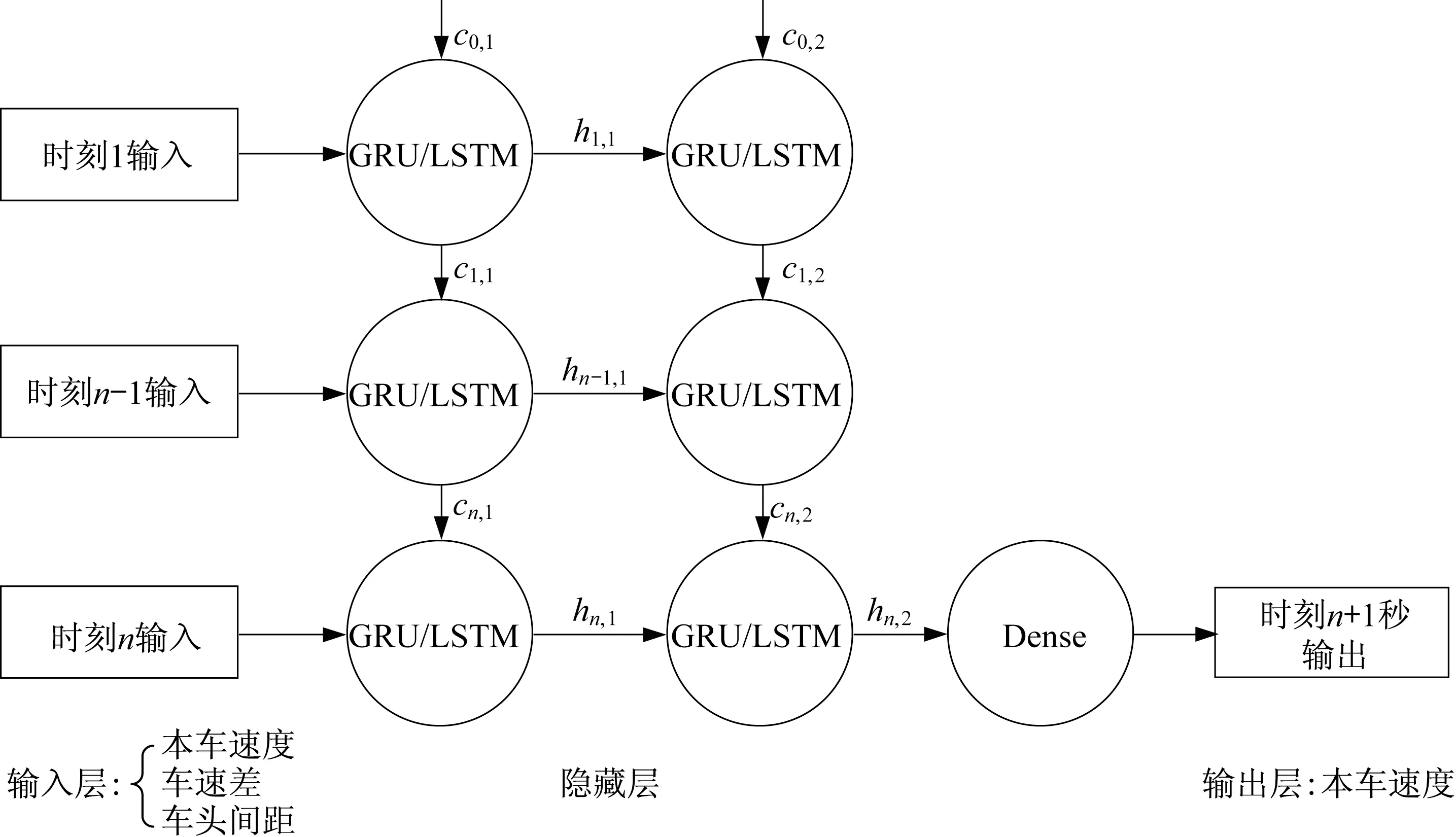
图4 深度学习神经网络结构Fig.4 Structure of deep learning neural network
2.3 模糊感知时间窗
通常,驾驶没有网联或精准环境感知功能的普通车辆的驾驶员无法精准感知周围场景,而是基于过往的驾驶记忆以及对场景一定程度的预测相结合,作为接下来采取行为的依据。如图5所示,驾驶员在进行跟驰决策时,需要不断对周围环境进行感知,之后大脑进行场景理解、跟驰决策,最后是跟驰行为执行。在基于理论的跟驰模型中,从开始感知t0到跟驰行为执行t1这一时间间隔,通常被称为反应时间τ,t1时刻的跟驰结果仅取决于t0时刻的跟驰状态。而在实际中,驾驶员在时间τ内,对跟驰场景的认知并不是真空状态,而是提前在心中对场景有一定的预期。本文将时间τ内的跟驰场景预期通过更早时刻的深度学习模型预测来模拟。
图6为具体的设计方案。其中,图6a为以往深度学习模型的输入输出时序关系,其通常将连续n个时刻的真实跟驰状态值作为输入,预测n+1时刻的输出。驾驶员过往的驾驶记忆通过输入时序的长短n来表示。以往深度学习模型没有对驾驶员反应时间间隔τ内的场景感知不确定进行模拟,而是将整个时段的真实跟驰状态值作为驾驶记忆,输入模型计算。过往时刻的真实跟驰状态值可以看作是驾驶员对跟驰场景的精确感知行为,这与驾驶员在反应时间τ内无法精准感知当前场景这一现象产生矛盾。同时,容易观察到的是,在相同跟驰情形下,同一驾驶员也不会产生完全相同的跟驰行为,原因之一是驾驶员的驾驶决策不完全是基于精确的跟驰场景感知。针对驾驶员在过往的驾驶记忆中,无法精确感知真实跟驰状态,本模型设计了模糊感知时间窗,如图6b所示,即在连续n个时间长度的真实跟驰状态数据中,将其中连续m(m≤n)个真实状态值通过对应时刻的模型预测值来代替,作为驾驶员对实际场景的估计,即模糊感知。模糊感知时间窗m的大小代表该时刻对场景感知不确定的程度。当m为0时,说明,驾驶员该时刻可精准感知过往驾驶状态,当m=n时,说明驾驶员当前时刻对过往场景的认知程度十分不确定。m的具体取值可以根据实际情况取0到n之间的固定值或不同时刻随机取范围内不同整数值。模型预测的最早输出时刻同时受输入时序长度以及模糊感知时间窗大小影响,当模糊时间窗大小m取0时,最早可预测第n+1时刻本车跟驰行为,当m=n时,最早可预测第2n+1时刻本车行为。

图5 跟驰决策思维认知模拟图Fig.5 Cognitive simulation of car-following decision making

图6 模糊感知时间窗设计图Fig.6 Diagram of fuzzy perception time window
2.4 参数设置
模型的训练流程主要包括数据准备、模型训练和模型超参设计。
在路段2所提取出的符合要求的94条数据中集中,取前85条作为训练集,其中20%的训练集数据作为验证集,以防过拟合。文献[8]得出驾驶员受1.0~3.5 s的记忆影响。因此,设计输入时序长度为3 s,以0.2 s为一个时间单位,则每次输入15个时刻的特征。
在模型训练中,损失函数f选取预测值与真实值的均方误差(mean squared error,MSE):
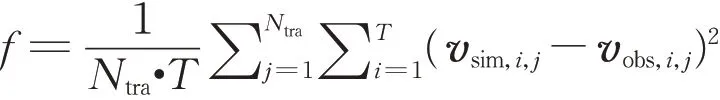
其中:Ntra为训练的跟驰对个数;T为每对跟驰对的训练次数,其值取决于跟驰片段总长度与输入时序长度之间的时间单元个数之差,本文跟驰片段总长度15 s,共75个时刻值,与初始输入时序时刻数量之差为60;vsim,i,j以及vobs,i,j分别为每对跟驰对j每个时间步长i预测后的速度预测值以及对应的真实值。优化算法选择Adam算法。设置训练迭代次数为500代,每一批次输入训练数据32组。参数patience为10,即在连续10次训练中内,验证集损失函数均未提升的话,则自动停止训练。保留后9条跟驰对作为测试集,用于对模型评估。
模型单元结构间权重及系数可以通过训练优化,然而模型中还存在一些参数,需要在训练前确定,这些参数被称为超参,其取值对结果有着不同程度的影响。模型的网络结构超参是指模型中隐藏层层数以及每层中GRU/LSTM单元输出维度,两者数量越多,对数据的学习能力越强,但网络会更加复杂,训练时间将极大延长且容易出现过拟合。如表1所示,本文将通过对GRU、LSTM两种循环神经网络分别设计1层、2层、3层隐藏层神经网络,各层网络中神经元输出维度从{16,32,64}中进行选取,从而选出适用于本数据集的模型结构。

表1 不同模型结构Tab.1 Structure of different models
2.5 评价指标及训练结果
对表1中分别以LSTM以及GRU为单元的5种不同模型结构进行训练,以损失函数MSE以及平均绝对误(mean absolute error,MAE)为模型预测结果评选指标,训练结果如图7所示,
图中横坐标模型序号与表1相对应,可看出,无论LSTM还是GRU,单层模型1-3均比多层模型指标优。经多次实验,发现1~2组的模型预测结果呈锯齿状,不够平滑;部分多层神经网络结构训练后,有时无法对测试集进行有效预测,而单层32维输出的LSTM以及GRU对结果的预测均有不错表现。鉴于相同规模网络,GRU网络参数个数约为LSTM网络的3/4,故选择以GRU为单元的网络结构3为最终网络。该网络经过154次循环后自动停止计算,验证集损失函数为0.656 5,MAE为0.178 9。图8是训练后的模型序号3、单元块为GRU的模型,对9个测试片段本车速度值预测结果,用Ntrail的值来表示不同的测试片段。在每个测试片段中,两条曲线分别为后车真实值以及预测值,图8与图9中每个测试片段的横坐标均为以0.2 s为单位的时间间隔,纵坐标为速度。通过将本模型选取的三维时间序列数据用于模拟驾驶员驾驶记忆后,模型在各个跟驰场景上都可以很好地进行预测。
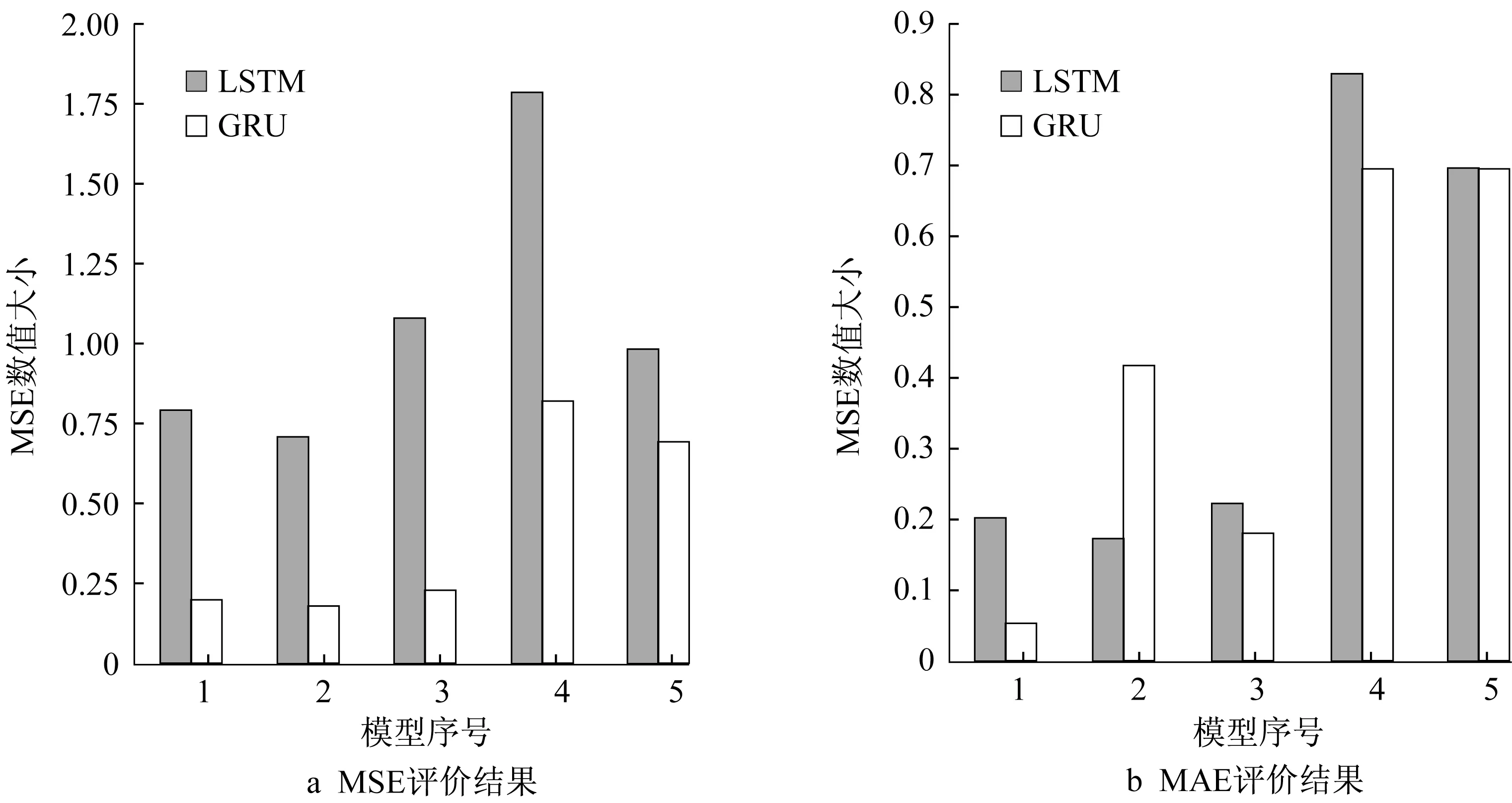
图7 模型性能比较Fig.7 Comparison of performance of models
3 仿真实验
3.1 多场景下的模糊感知仿真
为验证文中设计的驾驶员场景期望行为,设计0.2 s的模糊感知时间窗,对测试集中片段1~9的跟驰场景进行计算,结果见图9,三条曲线分别代表前车速度变化,后车精确感知下速度变化及后车在0.2 s模糊感知下的速度变化。结合图8、图9观察,可知,在不同跟驰场景下,0.2 s模糊感知下的驾驶员行为曲线变化与本车真实速度值、精确感知下速度变化趋势相似,但又有所不同,可作为驾驶行为异质性的一种表现,验证模糊感知下的深度学习模型对测试集也有较好的结果。
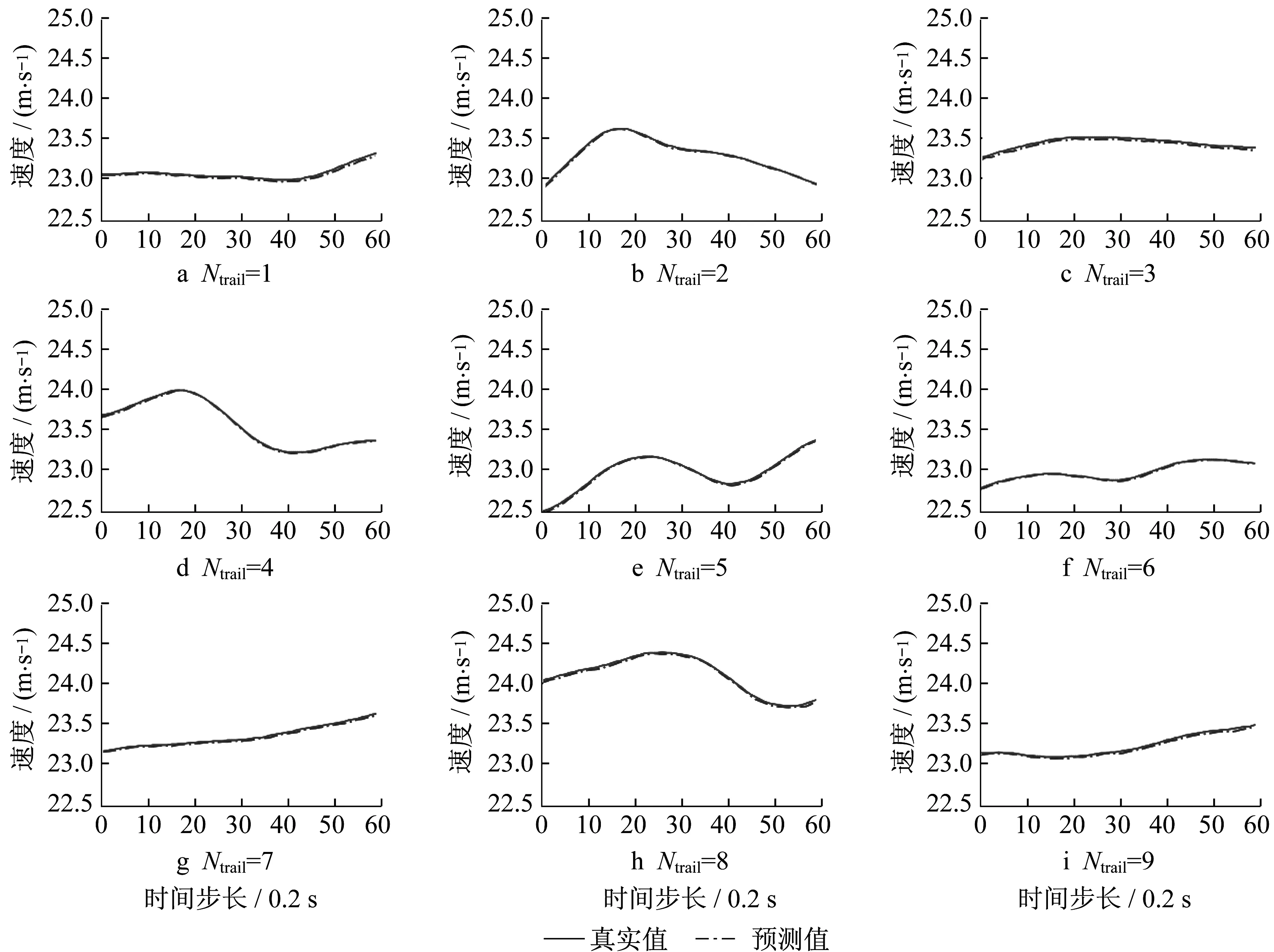
图8 GRU模型拟合结果图Fig.8 Diagram of model with GRU unit fitting results
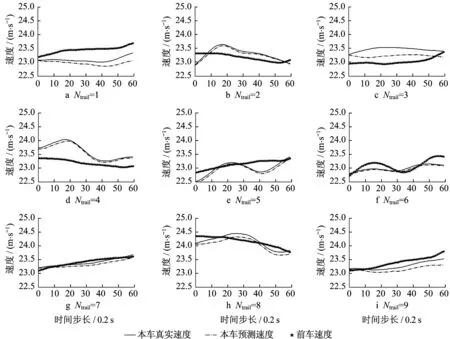
图9 不同场景下的模糊感知仿真结果Fig.9 Simulation results of fuzzy perception in different situation
3.2 多步模糊感知时间窗仿真
为模拟驾驶员在同一场景不同模糊感知下的跟驰行为,将模糊感知时间窗从0.2 s依次递增到3 s。以片段4跟驰场景为基准,前车在0~12 s期间以23.36 m·s-1小幅减速至23.07 m·s-1,后车在开始阶段,车头间距为33.65 m。真实场景中的后车行驶速度在23.25~24 m·s-1之间。所得结果如图10所示,实线代表前车信息,虚线为不同模糊感知时间窗大小下的仿真结果,可代表同一驾驶员在相同场景可能产生的不同跟驰行为。同模糊时间窗下的模拟轨迹,从位移图可以看出,在各模糊窗大小下,后车行为均与前车保持稳定的跟驰状态。从速度以及加速度曲线可以看出,在0.4~1 s的模糊时间窗内,得到的跟驰轨迹会较早地进行较大幅度的减速,从而保持较大的安全距离;而其余模糊时间窗的跟驰速度在前车速度值附近波动,对应的车头间距也较小。对其他跟驰片段进行同样的操作,也会产生类似跟驰行为,验证模型可在同一场景下生成不同且安全的跟驰行为。通过模型分析及多次重复实验可知:模型训练结束后,内部参数是固定的,调节不同的时间窗大小,会生成不同的异质跟驰行为。对于相同的场景,不同实验组之间只要确保每步预测设定相同的时间窗,就可得出相同的实验结果。

图10 多步模糊感知时间窗仿真Fig.10 Simulation results with different fuzzy perception windows
3.3 模型可迁移性仿真
3.1~3.2节中的实验均为对highD中提取出的数据集进行拟合及仿真,为进一步测试模型可迁移性,即在未知场景中,验证模型是否可得出合理结果。设计如下跟驰场景,在单车道公路上,0~3 s时,前车以22 m·s-1速度行驶,随后以2 m·s-2的减速度减速1 s,在4~9 s期间,以20 m·s-1速度匀速前行,在9~12 s期间,以1 m·s-2加速度加速至23 m·s-1,随后以23 m·s-1匀速前行。初始时刻,后车与前车车头间距45 s,后车在0~3 s期间,以22 m·s-1匀速前行,用来模拟初始阶段的驾驶记忆。仿真结果如图11所示。
图11中,4个子图分别代表两车速度、车头间距、位置以及加速度变化。对仿真的后车行为进行分析:在0~3 s期间,前车速度大于后车,因此,车头间距逐渐增大。为保持与前车的跟驰状态,后车以将近2 m·s-2的加速度加速行驶,因此,在3~10 s之间,车头间距逐渐缩短。为保持一定安全距离,后车在5 s之后不断小幅度减速。由于前车在9~12 s,以1 m·s-2加速度加速至23 m·s-1,车头间距逐渐增大,因此,后车于12 s左右开始加速跟驰前车,在12 s之后,前车匀速行驶,后车逐渐保持速度平稳跟驰。从上述分析中,仿真的跟驰行为具有合理的解释性,且跟驰过程中不会与前车产生碰撞,因此可较好模拟驾驶员的跟驰行为。

图11 设计场景仿真结果Fig.11 Simulation results of designated scenario
4 结语
以往的深度学习跟驰模型输出可看作是通过学习大量输入数据规律,并平均后的预测结果。而真实场景中,即使同样的驾驶员在相同场景下跟驰前车,由于驾驶记忆、感知不确定及其他潜在因素影响,其每次跟驰行为也会存在差异。
本文基于精度更高的highD数据集,通过提取符合条件的跟驰片段。设计了不同结构的GRU/LSTM深度学习模型。经训练,得出32个GRU或LSTM输出单元的单层神经网络,在精确的驾驶记忆条件下,可以很好地拟合真实数据。由于相同规模下,GRU参数比LSTM少,意味着更少的计算量及时间消耗,因此选择GRU模块作为模型基本单元。为验证模型的模糊感知特性,分别设计不同场景以及同一场景不同程度的模糊感知下的仿真实验,验证模型可适用于不同跟驰场景的模糊感知,且这些行为都具有一定稳定性和可解释性。无模糊感知时间窗的输入输出,更类似于精确感知场景下的智能网联车辆行驶策略,而增加模糊感知时间窗的深度学习模型,使得深度学习模型可在同一场景下,快速产生大量异质交通行为,有利于仿真研究异质驾驶行为导致的交通现象。
从数据输入的角度,本文处理后的跟驰片段较少,可能是导致多层LSTM及GRU模型结果不好的原因之一;由于提取出的跟驰片段,大多处于一定速度范围的稳定跟驰状态,没有其他场景如:从静止状态加速以及急减速等场景,因此,导致所训练的模型,仅可有效模拟一定场景下的跟驰行为。另一方面,限于篇幅,本文仅对驾驶员速度感知不确定下的跟驰行为进行研究,下一步可同时将其他刺激变量如:速度差、车间距等进行相应处理,分析不同刺激变量模糊感知下的跟驰特性,从而更加全面地模拟驾驶员模糊感知及跟驰行为。
作者贡献声明:
李林波:相关概念及方案讨论,论文语言组织;
李瑞杰:数据处理及分析,实验设计及初稿撰写;
邹亚杰:论文审阅,结果分析及建议。
