防雪栅与路基间距对路基积雪分布影响规律的数值模拟研究

刘庆宽，何书勇，贾娅娅，李海飞，冯耀恒，李飞强

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043；2.河北省风工程和风能利用工程技术创新中心，石家庄 050043；3.石家庄铁道大学 土木工程学院，石家庄 050043)

雪灾被认为是当今世界面临的十大灾害之一[1]。风吹雪灾害能够引起道路积雪、能见度降低、交通阻塞和道路结冰等问题，从而导致交通事件频发。道路雪灾害不仅威胁到行人的交通安全、增加了抗灾救灾的难度，也损失了大量的人力物力，严重制约了当地经济的发展。我国雪灾害十分严重，且灾害地区分布较广，尤其是近年来随着一带一路战略的实施和西部地区铁路的建设，道路风吹雪灾害的问题亟待解决，并且随着全球气候的变化，雪灾频发，严重威胁了我国西北地区人们的正常生产和生活，所以针对道路的风吹雪问题和其防护措施的研究刻不容缓。

李楚鹏等[2]运用数值模拟的方法对不同设置方式的防雪栅进行研究，以此分析公路风吹雪形成机理和挡雪板的防雪原理。李聪辉[3]通过Fluent软件对三种不同边坡坡率和三种不同高度下的路堤表面风速进行了数值模拟，得出了边坡坡率及路堤高度对路堤表面风速分布的影响。吴鹏等[4]运用Fluent软件，通过对防雪栅的水平距离、路堤高度以及边坡坡率等参数的设定进行研究，最终确定合适的模拟参数。王向阳[5]采用Fluent软件模拟路堤工程的风雪流场，分析了路堤高度、边坡坡率及入射风速的变化对路堤风速场的影响，结果表明：风速模拟值与实际观测值基本吻合，当路堤高度处于一定高度范围内时，采用高路堤、小边坡坡率等提高路堤面风速措施可有效减轻路面风吹雪灾害。Tabler[6]对缩尺比为1/30的防雪栅模型进行研究，发现模型积雪分布的实测结果与原型实测结果吻合较好。Anno[7]采用风洞试验的方式对缩尺比1/300的防雪栅模型进行风雪流研究，认为在跃移轨迹对试验结果影响较小的情况下，可放松弗劳德数的要求，并提出时间尺度和速度比参数，并且提出在对陡峭障碍物后方积雪进行试验时，来流湍流条件、地表粗糙度和粒子休止角等为重要相似参数。最终得到以活性黏土作为雪的模拟物可获得较好的试验效果的结论。苏国平[8]利用数值模拟的方法，模拟了路堑周边以及挡雪墙背风侧流场，又研究了挡雪墙的不同设计参数对路堑周围积雪的影响。

综上所述，以往有关道路风吹雪问题及其防护措施的研究对象大多是单个防雪栅、单个路基，而对防雪栅与路基的组合研究较少，本文采用数值流体计算的方法，以防雪栅与路基组合为研究对象，计算得到与防雪栅不同布置间距下路基周围的风速和其表面的剪切速度，据此分析路基表面的积雪分布情况，并将计算结果与现场实测结果进行对比来验证数值模拟的正确性，为道路风吹雪灾害的防治以及路基的建设提供理论基础。

1 研究概况

1.1 模型参数和工况

Naaim-Bouvet[9]和武鹤等[10]研究结果均表明透风率在50%～66%的防雪栅防雪效果最好。考虑到现场实测条件，选用高度较低的防雪栅模型在短时间内更容易得到试验结果，因此，本文数值模拟和现场实测均选用透风率为60%，高为0.15 m的防雪栅模型。李鹏翔等[11-12]研究表明采用小边坡坡度的路堤和路堑可有效的减弱路基表面的风吹雪灾害，并且建议路基设计边坡坡度采用1∶1.5。本次试验选用边坡坡度为1∶1.5，高度(或深度)为0.2 m的路堤和路堑模型。

朱光耀[13]在《公路风吹雪雪害形成机理与防治》中规定在平坦地段上透风率为66%的防雪栅与道路距离应取20H1～25H1，其中H1为防雪栅高度。Tabler[14]给出了平坦地面上防雪栅与路基的串列布置间距和错列布置间距公式。本文在参考上述文献、结合现场实测条件以及现场多次测试等前提下，最终以能够在路基模型前后产生较好的积雪为依据而确定的布置间距，防雪栅与路基的布置间距分别定为1.5 m，2.0 m，2.5 m，3.0 m和4.0 m，即为10H1,13.33H1,16.67H1,20H1和26.67H1,其中H1为防雪栅高度。数值模拟的计算模型与现场实测模型一致。防雪栅尺寸如图1所示，路基模型尺寸以及防雪栅与路基的组合工况如图2所示。

图1 防雪栅模型图Fig.1 Snow fence model diagram

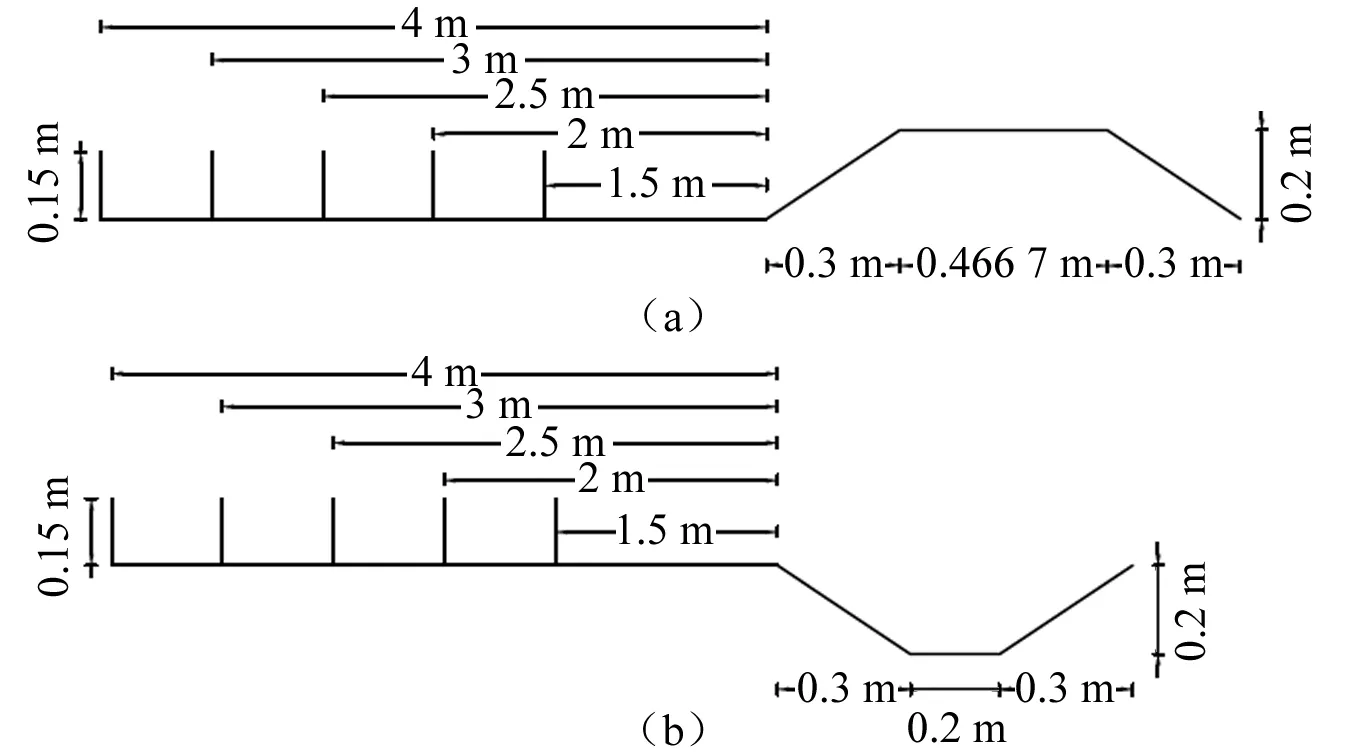
图2 防雪栅与路基的组合工况图Fig.2 Combined working condition diagram of snow fence and subgrade

1.2 数值模拟介绍

1.2.1 几何建模与计算参数

为了进一步分析防雪栅与路基间距对路基周围流场的影响规律，应用Fluent软件对5种布置间距下的路基表面风速进行模拟。Standardk-ε是最常见的湍流计算模型，模型本身具有的稳定性、经济性和比较高的计算精度，非常适合完全湍流的流动过程模拟[15-19]，因此所以本文选用Standardk-ε湍流模型。在数值模拟中对残差的设置主要是用来判断计算收敛性的标准，理论上残差越小越好，由于存在数值精度问题，不可能得到0残差，对于单精度计算一般应低于10-3以下才好，本文在计算的过程中选用残差为10-5。速度压力耦合采用SIMPLEC方法求解，本文选用的壁面函数为标准壁面函数。

路堤和路堑计算域尺寸以及边界条件的设置如图3所示，入口边界距防雪栅分别为路堤宽的20倍即21.34 m和路堑宽的20倍即16 m，出口边界距路堤、路堑也为路堤、路堑宽的20倍，上下边界距离取20倍的路堤、路堑高度，均为4 m。

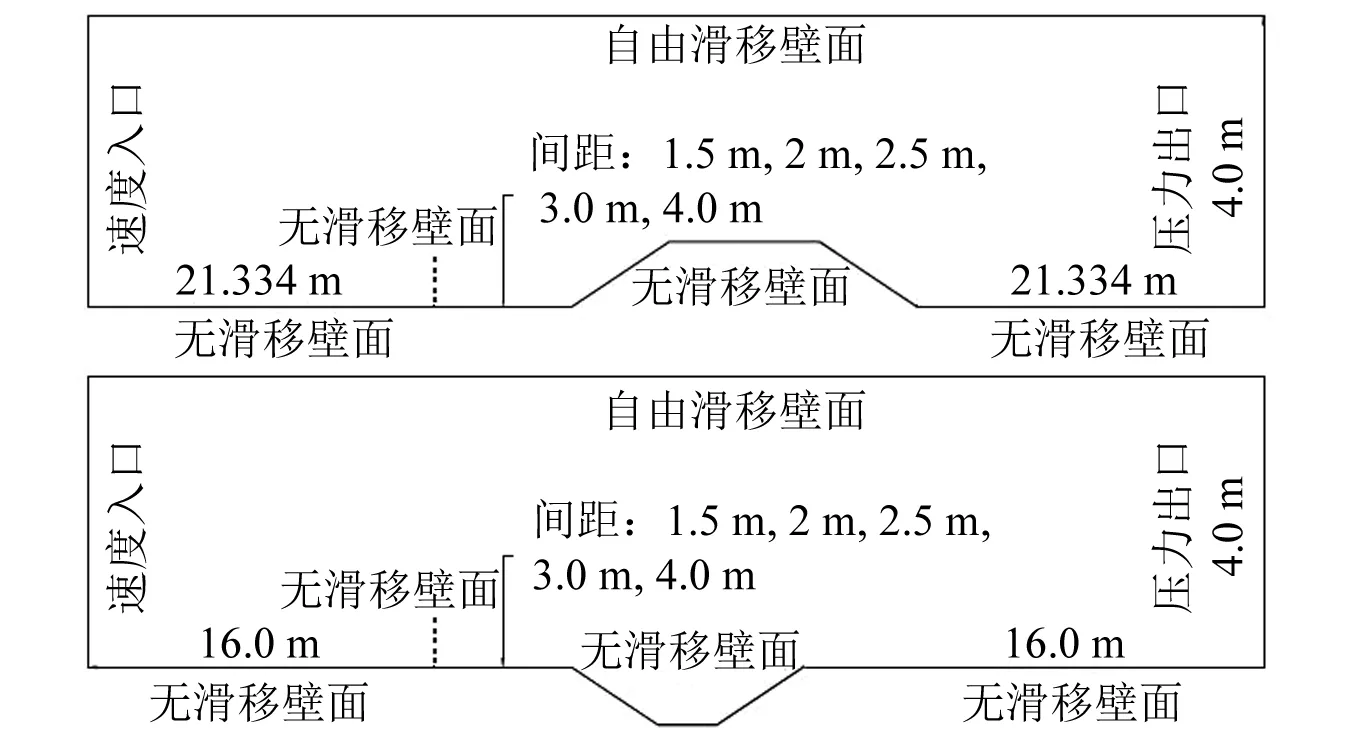
图3 路堤和路堑计算域及其边界条件示意图Fig.3 Schematic diagram of the computational domain and boundary conditions of embankment and cutting

考虑路基表面附近流场变化较为复杂，在近地面以及接近模型表面的一定高度范围内对网格进行加密。其中图4～图8为防雪栅与路基组合间距为3.0 m时模型周围网格划分情况，边界层最小网格尺寸为0.015 m，网格总数约为11万。其余工况最小网格尺寸均为0.015 m且网格总数也差别不是很大。

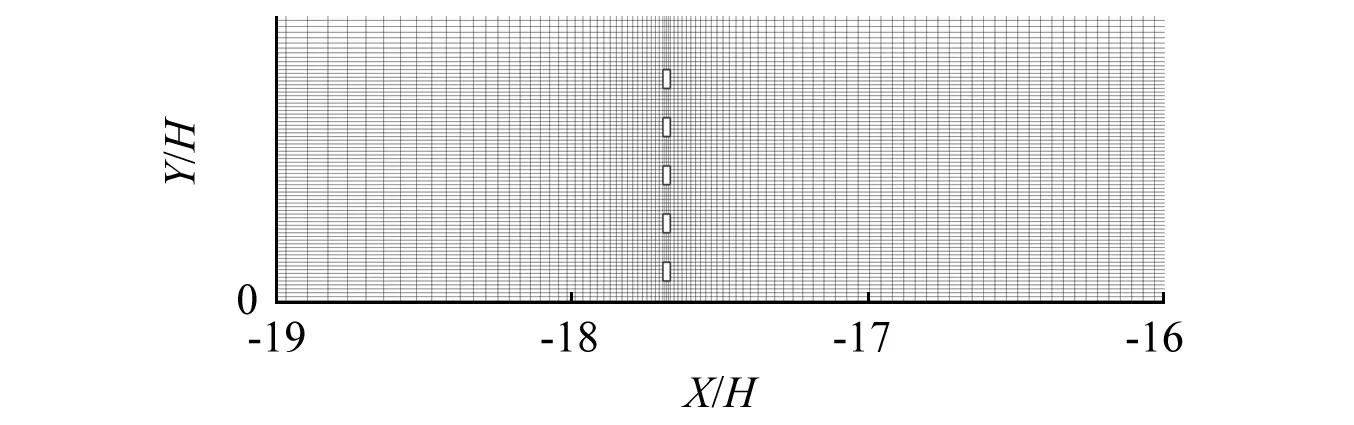
图4 防雪栅局部网格图Fig.4 Partial grid map of snow fence

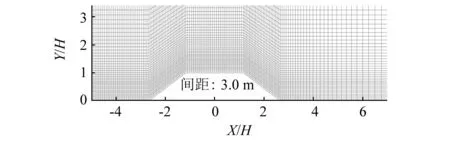
图5 路堤局部网格图Fig.5 Partial grid map of embankment

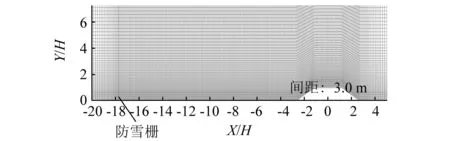
图6 防雪栅与路堤整体网格图Fig.6 Overall grid of snow fence and embankment

图7 路堑局部网格图Fig.7 Partial grid of cutting

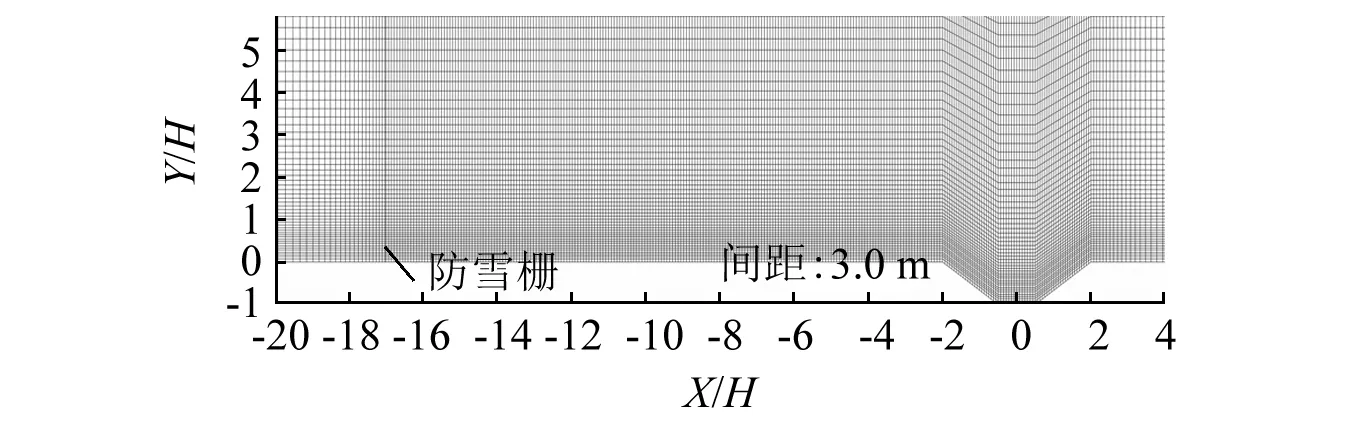
图8 防雪栅与路堑整体网格图Fig.8 Overall grid of snow fence and cutting

1.2.2 边界条件

(1)计算域入口设置为速度入口(velocity-inlet)，其中平均风速剖面、湍动能和湍能耗散率均采用用户自定义函数编程。风剖面采用指数率

U(z)=U1.5×z0.15

(1)

式中:U(z)为z高度处的风速；U1.5为1.5 m高度处风速，大小为8.2 m/s，此风速为现场实测所得平均风速；0.15为B类地貌的地面粗糙度指数。入口处的湍动能与湍动能耗散率的表达式分别为

(2)

(3)

(4)

式中:Cu为模型常数，大小为0.09；K为冯卡门常数，大小为0.42；Iu(z)为z高度处来流的紊流度；B类地貌下I10取0.14。

(2)计算域出口设置为压力出口(pressure-outlet)。

(3)计算域上边界设置为自由滑移壁面[20-22](slip wall)，对于本文数值模拟计算，上边界距离计算模型足够远，因此采用slip wall边界条件，并在设置中将此边界的剪切应力设置为零，变更为无滑移壁面，故此边界处法向速度和所有流动变量的法向梯度为零，等价于symmetry边界条件。

(4)计算域下边界和防雪栅以及路基表面设置为无滑移壁面(no slip wall)。

1.2.3 网格无关性检验

在数值模拟时，一般均需进行网格无关性检验，当网格数量增加对模拟结果影响可以忽略不计时，网格无关性则满足要求。本文采用4种不同数量的结构化网格来验证网格无关性，如表1所示。并采用布置间距为3.0 m工况的路堤周围流场进行比较，其结果如图9所示。

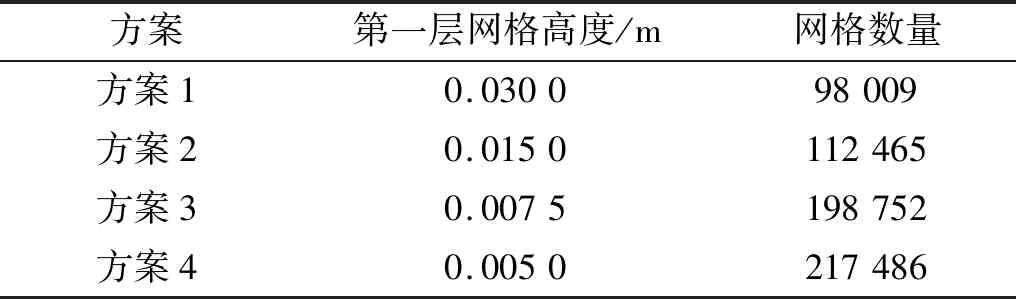
表1 计算方案Tab.1 Computational cases

图9可以看出4组方案计算所得路堤周围流场的总体趋势一致。随着第一层网格高度的不断减小，网格总数不断增加，4组方案的计算结果基本一致，则证明了网格无关性的要求。考虑到计算时间等原因，本文中所有计算工况均采用方案2的第一层网格高度。

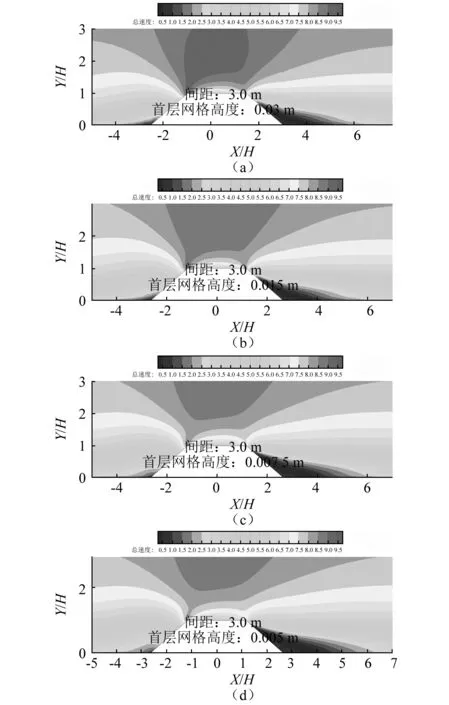
图9 网格无关性检验Fig.9 The grid independence test

1.3 现场实测介绍

本文实测的试验场地位于新疆塔城铁厂沟镇附近，当地地形平坦开阔(属于B类地貌)，雪源和风力充足，能够形成稳定的风雪流，满足本次试验的条件，是合适的实测场地。实测模型采用木质材料制作，模型端部设置有端板用来减小模型两端气流的绕流对试验结果的影响。实测模型的尺寸以及模型之间的布置情况均与数值模拟的模型尺寸和布置情况完全一致，见图1和图2。实测模型放置如图10所示，积雪的厚度由安装在模型表面带有刻度的钢钎读出。试验现场的风速由风速风向仪采集，如图11所示。

图10 现场模型放置图Fig.10 Picture of the placement of model in the field

图11 风速风向仪安装和放置图Fig.11 Picture of the installation and placement of anemometer

2 数值流体计算结果分析

2.1 流场结果及分析

在实际工程中，我们一般关注路堤和路堑周围的积雪分布情况，所以本次计算我们分析了路堤和路堑周围的流场分布。数值计算得到5种布置间距下路堤和路堑附近流场的风速等值线云图，如图12所示，为了方便观察计算结果，本文参考王向阳研究中风速减小区的规定方法，并结合本文数值计算结果以及实测积雪堆积区域，在此定义风速小于2 m/s的区域为风速减小区。

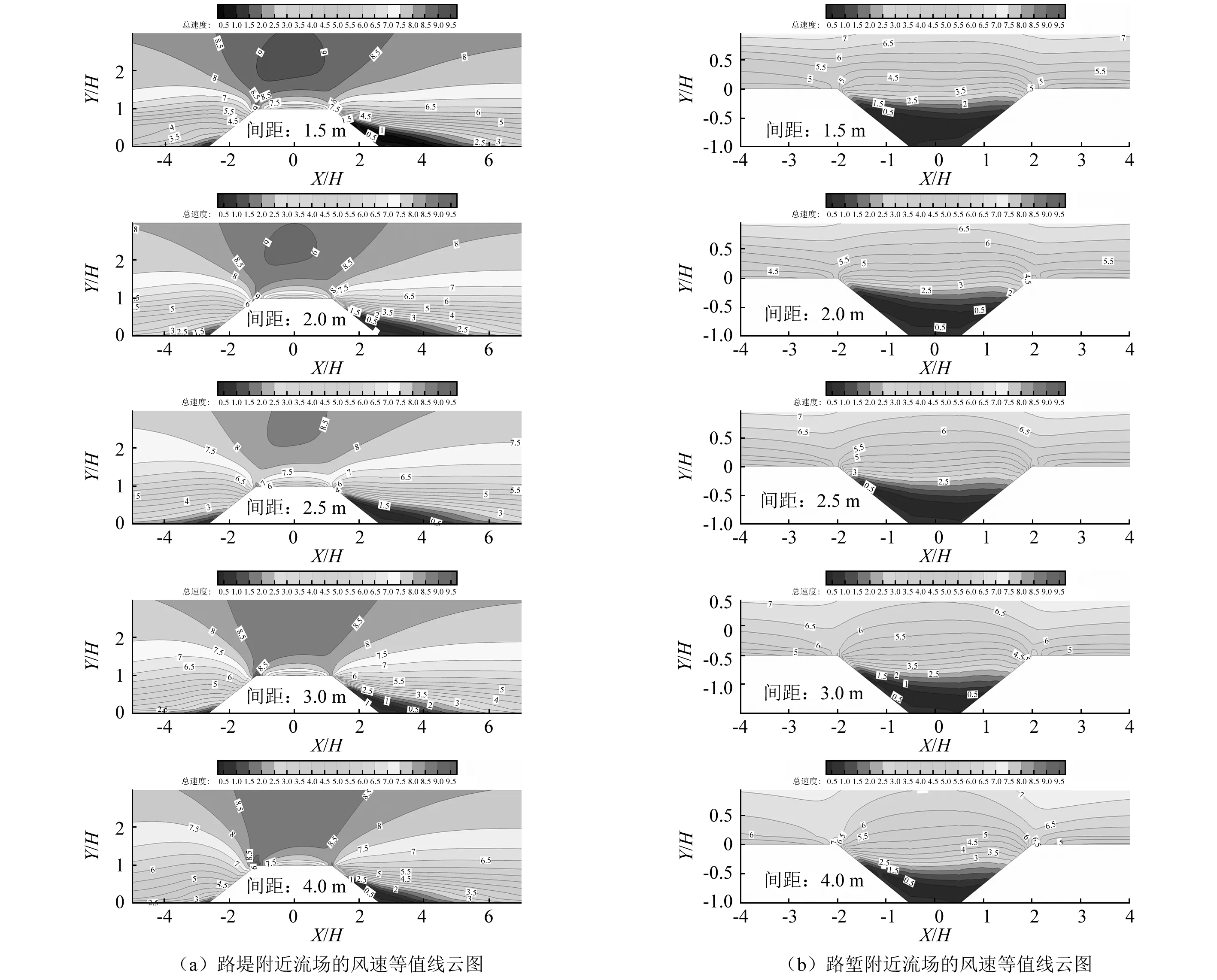
图12 5种布置间距下路堤和路堑附近流场的风速等值线云图Fig.12 Cloud contours of wind velocity contours of the flow field near the embankment and the cutting in 5 arrangement spacings

对于路堤而言，随着与防雪栅布置间距的增大，路堤上风侧和下风侧坡脚处的风速减小区范围均呈先增大后减小的变化趋势，但下风侧坡脚处的风速减小区均较上风侧坡脚处风速减小区范围大，当布置间距为2.5 m时(即16.67H1)，风速减小区范围达到最大，此时路堤两侧坡脚处积雪堆积范围也达到最大。此外，随着路堤与防雪栅布置间距的增大，上风侧路肩处、路面、下风侧路肩处附近风速基本保持不变。

对路堑而言，在与防雪栅5种布置间距下，路堑内部风速均较小，容易产生积雪堆积。随着与防雪栅布置间距的增大，路堑内风速减小区的高度有轻微降低趋势，但其内部风速减小区不易消除。

2.2 壁面剪切速度分析

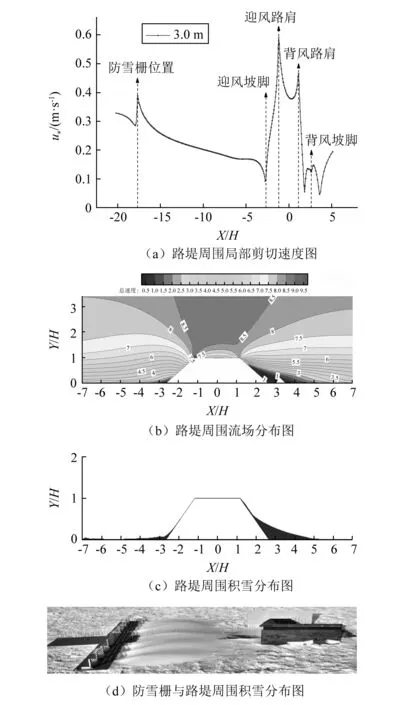
《风对结构的作用》[23]定义雪颗粒开始运动时雪颗粒表面的流动剪切速度u*为阈值剪切速度u*t。当u*>u*t时，雪颗粒才能移动，路基表面积雪会发生侵蚀；当u*=u*t时，雪颗粒处于将要移动但并未移动的临界状态；当u*

(5)

式中：τ为壁面剪切力；ρ为空气密度。

Kind[24]总结了不同状态下雪的阈值剪切速度，如表2所示。

表2 雪颗粒阈值剪切速度Tab.2 Threshold shear speed of snow particles

为了进一步研究不同防雪栅与路基间距对路基表面积雪的侵蚀与堆积的影响，计算得到与防雪栅5种布置间距下路堤、路堑表面的剪切速度，如图13、图14所示。图15具体分析了与防雪栅5种布置间距下路堤、路堑表面的关键位置处的剪切速度，并与Kind总结的3种雪颗粒条件进行对比，分析在3种雪颗粒条件下不同布置间距的路基表面雪颗粒堆积与侵蚀情况。

从图13可以看出，5种布置间距下路堤表面的剪切速度变化趋势基本一致，且均在路堤上风侧路肩和下风侧路肩处剪切速度达到极大值，在上风侧坡脚处、下风侧坡脚前后约0.8H处剪切速度达到极小值，其中H为路堤的高度。随着与防雪栅布置间距的增大，路堤表面各部分的剪切速度均呈先增大后减小又增大的趋势，且当布置间距为2.5 m时，路堤周围剪切速度达到最小。随着路堤与防雪栅布置间距的变化对路堤下风侧边坡的剪切速度影响较小。

图13 5种布置间距下路堤表面的剪切速度图Fig.13 Picture of shear velocity of embankment surface in 5 arrangement spacings

从图14可以看出，5种布置间距下路堑表面的剪切速度变化趋势基本一致，且均在路堑上风侧坡顶和下风侧坡顶处剪切速度达到极大值，在上风侧坡脚前约0.9H处、下风侧坡脚后约0.5H处剪切速度达到极小值，其中H为路堑的高度。随着路堑与防雪栅布置间距的增大，除下风侧坡脚处剪切速度呈先增大后减小的趋势外，路堑表面其余位置的剪切速度均呈增大趋势。

图14 5种布置间距下路堑表面的剪切速度图Fig.14 Picture of shear velocity of cutting surface in 5 arrangement spacings

图15(a)为5种布置间距下路堤表面关键位置的剪切速度图，图中虚线为Kind总结的三种条件下雪颗粒阈值剪切速度。随着与防雪栅布置间距的增大，除路堤上风侧坡脚处的剪切速度是先减小后增大外，路堤其余4个关键位置处的剪切速度均呈先增大后减小又增大的趋势，且均在布置间距为2.5 m(即16.67H1)的距离减到最小，此时路堤表面最容易产生积雪堆积，定义此间距为路堤与防雪栅组合的最不利间距。在这5种布置间距下，路堤表面剪切速度由小到大的位置分别是路堤上风侧坡脚、下风侧坡脚、路面中部、下风侧路肩和上风侧路肩处，所以路堤的两个坡脚处最容易产生积雪堆积，而上风侧路肩处的剪切速度最大，最不易产生堆积。

参照Kind总结的雪颗粒阈值剪切速度并结合图15(a)可知，在-2.5 ℃下的新鲜疏松的干燥雪和0 ℃的自然降雪这两种情况下，路堤的两个坡脚处的雪颗粒剪切速度均小于相应的阈值剪切速度0.15 m/s和0.25 m/s，此时路堤的两个坡脚处会产生雪颗粒堆积。而两个路肩处和路面中部这三个位置雪颗粒的剪切速度均大于相应的阈值剪切速度，这些位置不易积雪；同理，在0 ℃下降落几个小时的雪时，5种布置间距下路堤的上风侧坡脚、下风侧坡脚以及路面中部的剪切速度均小于阈值剪切速度0.4 m/s，这些位置易产生积雪堆积。在上风侧路肩处不易积雪；而在下风侧路肩处，除布置间距为2.5 m时产生积雪堆积外，其余布置间距下均不易积雪。

图15 5种布置间距下路堤和路堑表面关键位置剪切速度图Fig.15 Picture of shear velocity of the key position of embankment and cutting surface in 5 arrangement spacings

图15(b)为5种布置间距下路堑表面关键位置的剪切速度图，图中虚线为Kind总结的三种条件下雪颗粒阈值剪切速度。随着与防雪栅布置间距的增大，路堑的上风侧坡顶、上风侧坡脚和下风侧坡顶处的剪切速度不断增大。而路面中部和下风侧坡脚处的剪切速度先增大后减小。路堑表面的剪切速度由小到大依次是上风侧坡脚、下风侧坡脚、路面中部、上风侧坡顶和下风侧坡顶处。所以对于路堑来讲，一般路堑的两个坡脚处最容易产生积雪堆积，两个坡顶处最不易产生积雪堆积。当防雪栅与路堑的间距超过2.0 m时(即13.33H1)，随着路堑与防雪栅布置间距的增大，路堑的路面中部和下风侧坡脚处的剪切速度不断减小，则路堑内的积雪堆积也会不断减小。

参照Kind总结的雪颗粒阈值剪切速度并结合图15(b)可知，在-2.5 ℃下的新鲜疏松的干燥雪和0 ℃的自然降雪这两种情况下，路堑的上风侧坡脚、路面中部和下风侧坡脚处的雪颗粒剪切速度均小于相应的阈值剪切速度0.15 m/s和0.25 m/s，此时路堑的两个坡脚处和路面中部会产生积雪堆积。而上风侧坡顶和下风侧坡顶处雪颗粒的剪切速度均大于相应的阈值剪切速度，这两个位置均不易产生积雪堆积；同理，在0 ℃下降落几个小时的雪这种情况下，5种布置间距下除了下风侧坡顶处的剪切速度大于相应的阈值剪切速度0.4 m/s外，其余4个位置的剪切速度均小于相应的阈值剪切速度，所以此时下风侧坡顶处不易积雪，其余位置均易产生积雪堆积。

3 现场实测结果验证

为了验证数值模拟的正确性，用现场实测中布置间距为3.0 m的工况结果与数值模拟中相应工况结果进行对比。如图16所示，其中图16(c)为图16(d)所对应的路堤周围积雪分布图，图16(c)中阴影区域为积雪堆积区域。

由图16(a)知，由于气流受到防雪栅的阻挡，在靠近防雪栅前后两侧的剪切速度有变小趋势，在距路堤5H处，剪切速度趋于平缓且不发生明显改变，但随后在靠近迎风坡脚处剪切速度急剧下降，并在迎风坡脚处降到最低，迎风坡脚处产生积雪堆积。路堤的两个路肩处剪切速度较大，一般不产生积雪堆积。背风侧坡脚周围的剪切速度相比迎风坡脚处剪切速度小，所以背风坡脚处产生的积雪较迎风坡脚处多，以上分析结果与现场实测堆积结果一致。由图16(b)和图16(c)对比可知，图16(b)中的风速减小区范围与图16(c)中的积雪堆积区域有很好的对应关系。

图16(d)为防雪栅与路堤周围积雪分布图，从图中可清晰地看出防雪栅对积雪的阻挡效果，雪颗粒在防雪栅后一定距离处开始堆积，并且堆积厚度先增大后变小，到距路堤一定位置处不再积雪，直到在靠近路堤上风侧坡脚处又开始堆积。分析原因是由于风雪流流经防雪栅时，受到了防雪栅的阻挡，在防雪栅前风速和剪切速度开始下降，并在防雪栅后侧形成风速减小区，且此区域内剪切速度也不断降低，当风雪流远离防雪栅之后，受防雪栅影响越小，风速和剪切速度逐渐恢复变大，积雪堆积厚度也越来越小，直到当风雪流流经路堤时，风雪流又受到路堤上风侧的阻挡，并在路堤上风侧坡脚处形成风速减小区且剪切速度达到最小，产生积雪堆积。数值模拟结果很好地解释了现场实测中积雪的堆积现象，验证了数值模拟的正确性。

图16 3.0 m间距下路堤数值模拟结果和现场实测结果图Fig.16 Numerical simulation results and field measured results of embankment at a distance of 3.0 m

4 结 论

本文主要应用了数值模拟的方法研究了防雪栅与路基的布置间距对路基表面积雪分布的影响，最后再用现场实测结果来验证数值模拟结果，主要得到以下结论：

(1)对于路堤而言，5种布置间距下路堤周围流场和其剪切速度有很好的对应关系。从流场角度分析，路堤表面积雪部位按堆积程度由大到小分别是路堤下风侧坡脚、上风侧坡脚、路面中部、下风侧路肩和上风侧路肩处。从剪切速度角度分析，根据路堤表面剪切速度的大小，可从雪颗粒运动机理上判断路堤表面产生积雪堆积的先后顺序分别是路堤上风侧坡脚、下风侧坡脚、路面中部、下风侧路肩和上风侧路肩处。随着与防雪栅布置间距的增大，路堤两个坡脚处的风速减小区范围均呈先增大后减小的变化趋势；路基表面各部分的剪切速度均呈先增大后减小又增大的趋势，所以当透风率为60%的防雪栅与路堤布置间距为16.67H1时，路堤周围更易产生积雪堆积，定义此间距为该透风率下的防雪栅与路堤的最不利组合间距。

(2)对于路堑而言，5种布置间距下路堑内部均有风速减小区，且路堑周围流场和其剪切速度有很好的对应关系。从流场角度分析，路堑两个坡脚处最容易产生积雪堆积，两个坡顶处最不易产生积雪堆积。从剪切速度角度分析，路堑内部产生积雪堆积的先后顺序分别是路堑上风侧坡脚、下风侧坡脚、路面中部。随着与防雪栅布置间距的增大，路堑内的积雪堆积会不断减小，但是路堑内部积雪不易消除，因此防雪栅对路堑的挡雪效果不佳。

(3)运用剪切速度从运动机理上能够清晰地判断路基表面的积雪堆积与侵蚀，目前把雪颗粒的运动机理与工程实际结合的研究较少，建议今后在风吹雪灾害频发地区修建铁路前可先采用此方法并结合当地的雪颗粒属性以及气象条件对工程表面的积雪堆积与侵蚀进行预判断，则可以合理确定防雪栅与路基的布置间距，减少不必要的经济损失。

(4)数值模拟结果的风速减小区范围和剪切速度与现场实测积雪堆积区域有很好的对应，很好地验证了数值模拟结果的正确性。