直接接触式水箱中导流板结构优化研究

2021-03-31汪宁范誉斌张春伟张学军赵阳

制冷技术 2021年1期

汪宁，范誉斌，张春伟，张学军，赵阳

（浙江大学制冷与低温研究所，浙江省制冷与低温技术重点实验室，浙江杭州 310027）

0 引言

直接接触式热质交换目前已广泛应用于空调行业的直接蒸发冷却器、喷水室以及冷却塔等设备中[1-3]，其原理是空气与水直接接触进行传热传质，调节空气温湿度，调节效果取决于流体的热质交换效率，而设备中导流板结构对热质交换效率影响很大[4]。因此，为增强设备的传热传质、减小流动阻力、提高设备综合性能以及优化导流板结构具有一定的工程意义。

目前国内外对导流结构的研究主要集中在各类换热设备的强化换热[5-6]和弯管内气流分布[7-8]等方面。程友良等[9]采用FLUENT 软件建立了风机出口加装导流板的空冷单元物理模型，并对流动和传热进行分析，结果表明导流板可提高流场均匀性，强化换热。刘景成等[10]基于正交试验进行仿真实验，结合遗传算法与反向传播算法（Back Propagation，BP）神经网络，对板翅式换热器入口的导流结构进行了多目标优化分析，结果表明优化的导流结构可以显著提高流体的流动均匀性。ZHANG 等[11]应用数值模拟软件研究了弯管不同位置导流片诱导风流的影响，确定了理想的导流片安装位置。吴静玮等[12]对板翅式换热器中一种多级导流封头的分配特性进行研究，结果表明，该导流封头结构可明显改善换热器的分配特性；空气与水直接接触的传热传质研究主要包括热质交换过程的计算模型[13]和实验研究[14]两方面。SOBIN 等[15]对空气与水薄层逆流的热质交换过程进行研究，根据边界层理论和经验公式计算得到了热质交换系数，结果与实验数据较符合。SURESHKUMAR 等[16]建立了空气与液滴间传热传质双向耦合的仿真模型，并将模拟结果与前期的实验数据对比，结果表明该模型在研究范围内具有可靠性。由上述相关学者的研究发现，目前对导流板的研究主要集中在换热器和弯管流动的单相流领域，在空气-水直接接触式空气处理设备中的研究较少，导流板对流体流动与传热传质耦合影响分析较为缺乏。

针对上述问题，本文以直接接触式热质交换水箱结构为研究对象，采用正交试验法设计实验方案，结合计算流体力学软件FLUENT，研究导流板对空气与水之间热质交换效率以及流动阻力的影响，并基于提出的综合评价指标对结构进行优化。

1 数学模型

1.1 物理模型

水箱是直接接触式热质交换设备的关键部件，空气流经水面与水进行热质交换，可通过控制水温来调节出口空气的温湿度。在水箱中布置导流板改变空气流动的方向，提高流场的均匀性，强化换热。为了研究水箱中导流板结构参数对空气与水之间的传热、传质以及流动的影响，本文研究直接接触式水箱的结构如图1所示。

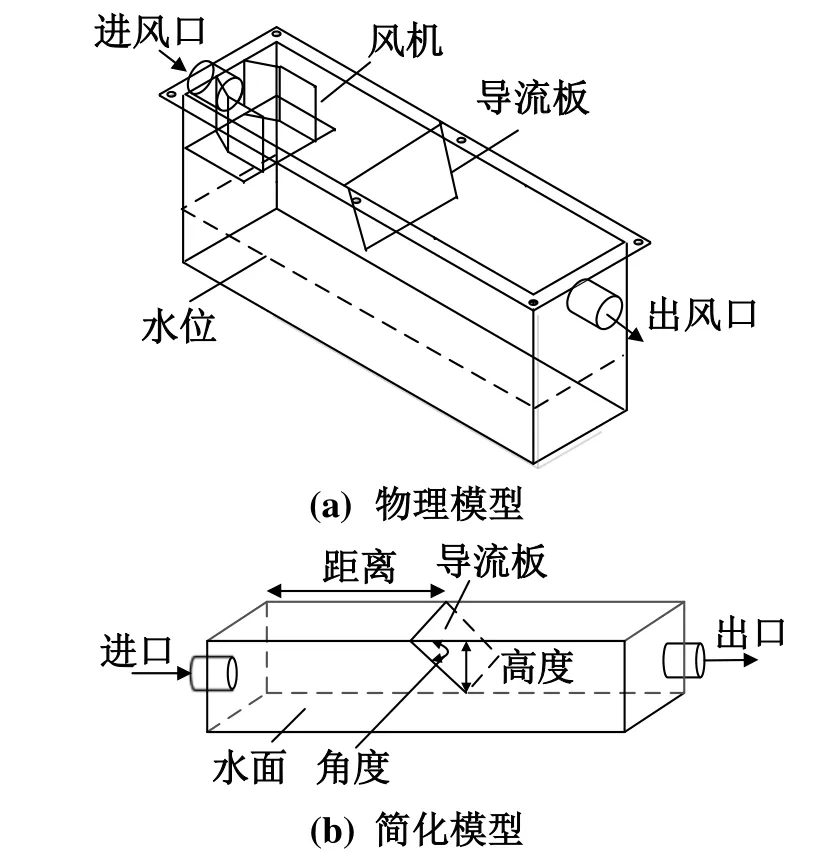
图1 直接接触式水箱的结构

图1(a)为热质交换水箱的物理模型，底部盛有一定量的水，进风口处布置风机，空气经进风口进入水箱，在导流板的作用下与水面进行充分的热质交换，处理后的空气经出风口流出水箱。水面距水箱顶部的高度为40 mm，空气与水面接触的横向距离为250 mm，水箱宽度为80mm，进风口和出风口直径均为21 mm。水箱中导流板的垂直高度、倾斜角度和安装位置距进风口距离可决定导流板在水箱中的位置与结构。为便于建模计算，对水箱模型进行简化，图1(b)为简化后的水箱模型。

1.2 计算模型

利用ICEM CFD 对水箱模型进行三维建模并划分结构化网格，由于水箱内部结构不规则，采用分块网格划分，进出口处划分O 型网格，并在交界面处进行界面处理，最终保证所有网格质量在0.6以上，较为理想。采用数值模拟软件FLUENT 对水箱模型进行数值计算，为便于分析，根据空气与水之间的热质交换原理[17-18]，作如下假设：1）湿空气的传热传质及流动过程处于稳态；2）忽略水箱内水面的微小波动，水面为一层均匀分布的饱和空气层，温度等于水温；3）忽略冷凝水对流动的影响，计算域为水蒸气和干空气组成的湿空气混合物；4）湿空气为不可压缩理想气体，即密度和比热容等参数在计算过程中为定值；5）忽略空气、水与水箱外环境的换热；6）不考虑空气流动过程的黏性耗散。

根据上述假设，可得多组分混合气体稳态流动的控制方程。

连续方程：

动量方程：

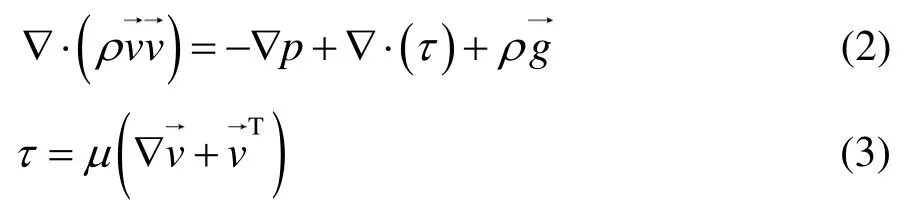
能量方程：

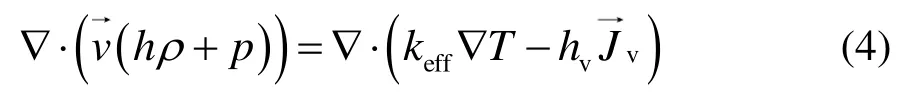
组分方程：

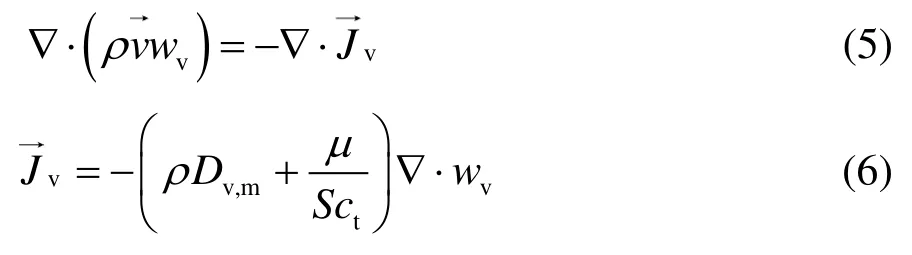
式中，ρ为混合物的密度，kg/m³；v为混合物的速度矢量，m/s；p为静压，Pa；τ为应力张量；g为重力加速度，m/s2；μ为动力黏度，Pa·s；h、hv分别为混合物、水蒸气的比焓，J/kg；keff为有效导热系数，W/(m·K)；T为混合物的温度，K；Jv为由浓度和温度梯度引起的水蒸气质量通量，kg/(m2·s)；wv为水蒸气的质量分数；Dv,m为水蒸气的质量扩散系数，m2/s；Sct为施密特数。

模型数值计算开启多组分输运模型，湍流计算选用标准k-ε模型，边界条件采用速度入口和压力出口，给定入口温湿度，水面采用定壁温边界，其水蒸气质量分数为水温对应的饱和湿空气中水蒸气质量分数，其它壁面采用无速度滑移绝热边界。压力速度耦合采用SIMPLE 算法求解，能量、动量和组分方程的离散均采用二阶迎风格式。

2 模型验证

2.1 网格无关性检验

网格划分会影响数值模拟计算结果，理论上网格划分越精密，计算精度越高。但是在实际计算中，受计算条件限制，网格划分小会导致计算量和浮点运算误差增加。因此，需要对模型的网格进行无关性检验，兼顾计算精度与计算成本，寻找合适的网格划分尺寸。

在相同的初始条件和边界条件下，以出口空气温度为目标对计算模型进行网格无关性分析。由于本研究物理模型数量较多，图2给出了其中一种模型在不同网格数量下出口空气温度的计算值对比。由图2可知，随着网格密度增加，出口空气温度逐渐上升，当网格数量在1×105以上时，空气温度已无显著变化。因此，综合考虑计算成本与计算可靠性，最终采用网格数量为51,323 的网格尺寸进行后续研究。

图2 网格无关性分析

2.2 模型准确性验证

为验证数值计算模型的可靠性和计算结果的准确性，将数值计算结果与文献的实验数据进行对比[19]，实验条件如表1所示，给定了水箱入口空气流动的雷诺数Re、入口温度ta,i、入口相对湿度φa,i和水温ts。

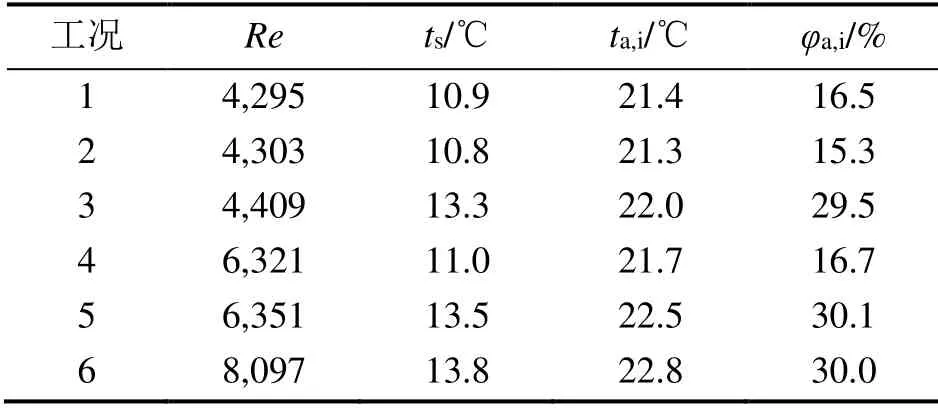
表1 实验条件[19]

根据表1中的实验条件，采用上述计算模型模拟水箱内空气与水间的传热传质现象，计算得出口空气温度和相对湿度。图3给出了实验值与模拟计算值的对比，由图3可知，水箱出口空气温度ta,o的模拟值均低于实验值，相对误差在-3%内，平均偏差为0.17 ℃；空气相对湿度φa,o模拟值均高于实验值，相对误差在+10%内，平均偏差为1.62%，且两者整体趋势基本相同。模拟与试验间偏差可能源于数值模型的简化处理以及实验测量误差，均在可接受范围内。综上所述，本文建立的数值计算模型可用于后续的研究。

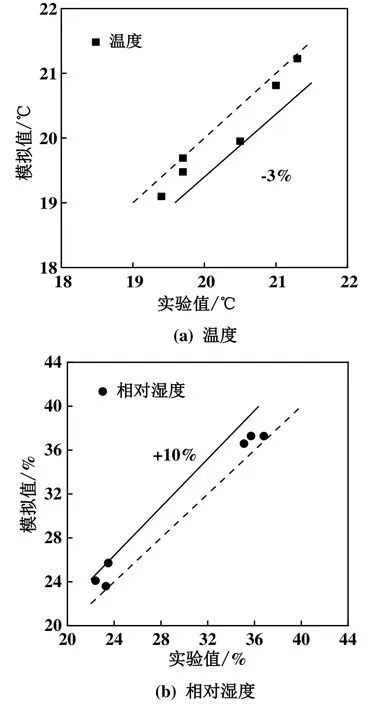
图3 实验值与模拟值对比

3 正交试验设计与模拟结果分析

3.1 正交试验设计

正交试验设计法是一种基于数理统计、概率论和实验，选用代表性实验点代替全面实验的研究方法，适用于多因素多水平的实验研究，可有效减少实验成本，提高研究效率[20-21]。为了研究水箱中导流板的垂直高度h、倾斜角度α以及安装位置距进风口距离x对空气流动与传热传质影响，对三因素进行正交设计，以空气与水之间的显热交换量Qs、湿交换量mv以及空气进出口压降Δp为目标进行试验。表2列出了三因素的实验方案，根据物理模型实际尺寸的限制，给出各因素4 个水平，并对水箱模型进行数值计算。

表2 导流板结构正交试验

采用极差分析法对上表16组正交试验结果进行分析，计算同一因素下不同水平的平均值，根据平均值求该因素的极差。对比同一因素不同水平的平均值，可得该因素下不同水平对目标函数的影响，对比不同因素极差的大小，可以得出不同因素对目标函数影响程度[22]。

3.2 结构参数对传热的影响

为研究导流板结构参数对空气与水之间传热的影响，对表2的实验工况进行数值模拟，根据式(7)计算空气与水间的显热交换量Qs：

式中，ma,i为空气的质量流量，kg/s；cp为空气定压比热容，J/(kg·K)。

表3所示为显热交换量Qs计算结果分析。

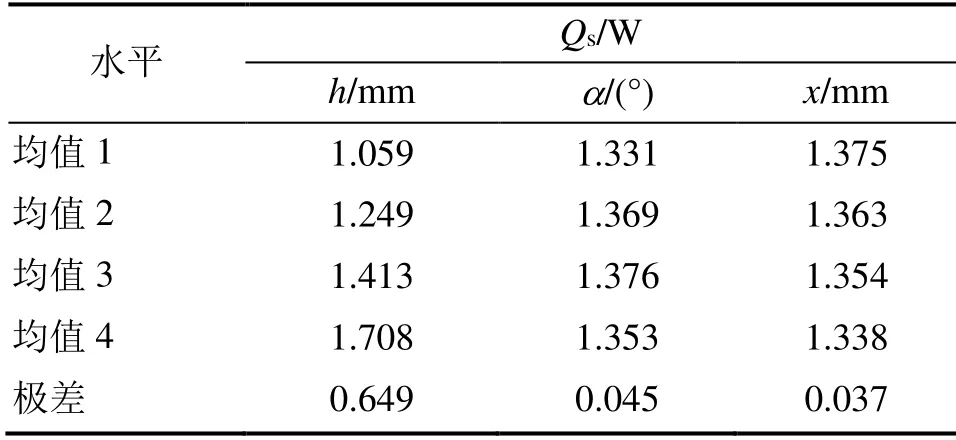
表3 显热交换量Qs 计算结果分析

由表3可知，导流板各因素对空气与水间传热的影响程度从大到小依次为：导流板垂直高度h、倾斜角度α、距进风口距离x。导流板倾斜角度和距进风口距离对空气显热交换量影响程度相近，约为垂直高度对显热交换量影响的1/14，说明导流板垂直高度的改变对空气与水间传热性能的影响较大，是影响空气传热的主要因素。导流板结构参数对传热的影响如图4所示。由图4可知，空气与水的显热交换量随导流板垂直高度的增加而增加，随倾斜角度的增加先增加后降低，转折点约为60°，随安装位置距进风口距离的增加而降低。在试验范围内，若只考虑空气与水之间的传热Qs，导流板结构参数的最优组合是高度h为35 mm，角度α为90°，距离x为60 mm，经验证，该组合下空气与水的显热交换量为1.79 W，高于上述16 组正交试验的显热交换量。

图4 导流板结构参数对传热的影响

3.3 结构参数对传质的影响

为研究导流板结构对空气与水之间传质的影响，根据式(8)计算湿交换量mv：

式中，wa,i、wa,o为进、出口空气的水蒸气质量分数。

对正交试验的模拟计算结果进行极差分析，分析结果列于表4。

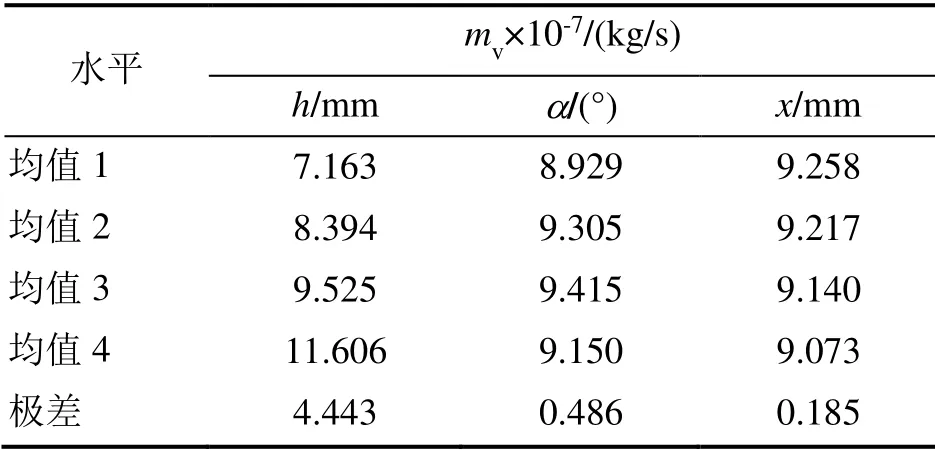
表4 湿交换量mv 计算结果分析表

由表4可知，导流板结构参数对空气与水的湿交换量影响从大到小的顺序为：导流板垂直高度h、倾斜角度α、距进风口距离x。与对传热影响规律类似，导流板垂直高度是传质的主要影响因素，倾斜角度和距进风口距离对传质的影响程度相近，约为垂直高度对传质影响的1/10，属于相对不敏感因素。

导流板结构参数对传质的影响如图5所示。由图5可知，空气与水的湿交换量随导流板垂直高度增加而增加，随倾斜角度增加先增加后降低，随距进风口距离增加而降低，与对传热的影响一致。在实验范围内，若以湿交换量mv为目标，最优组合为高度h为35 mm，角度α为90°，距离x为60 mm，经验证该组合的湿交换量为1.25×10-6kg/s，大于上述16 组正交试验的湿交换量。

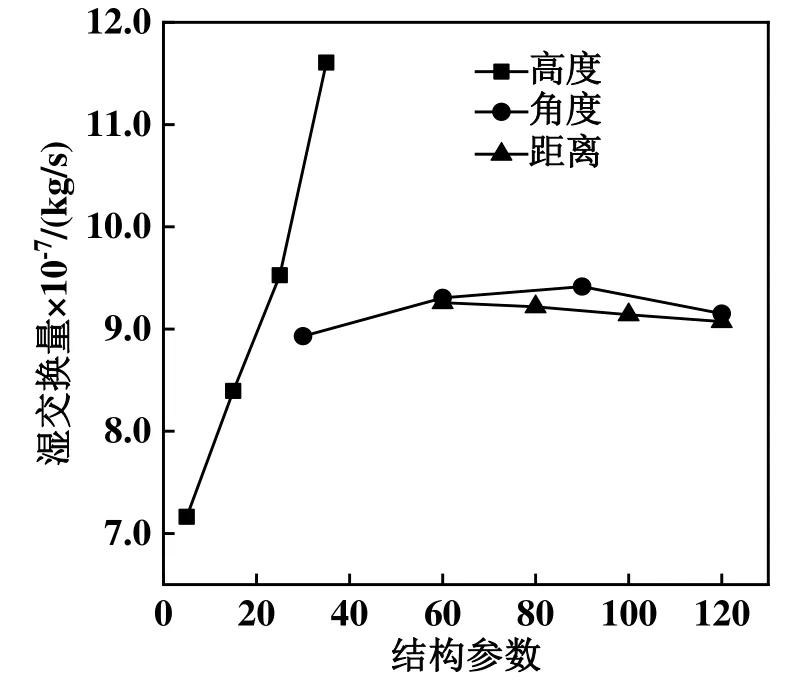
图5 导流板结构参数对传质的影响

3.4 结构参数对压降的影响

为研究导流板结构参数对空气流动阻力的影响，以水箱进出口空气的压降(Δp)为目标，对模拟结果进行极值分析，结果如下表5所示。

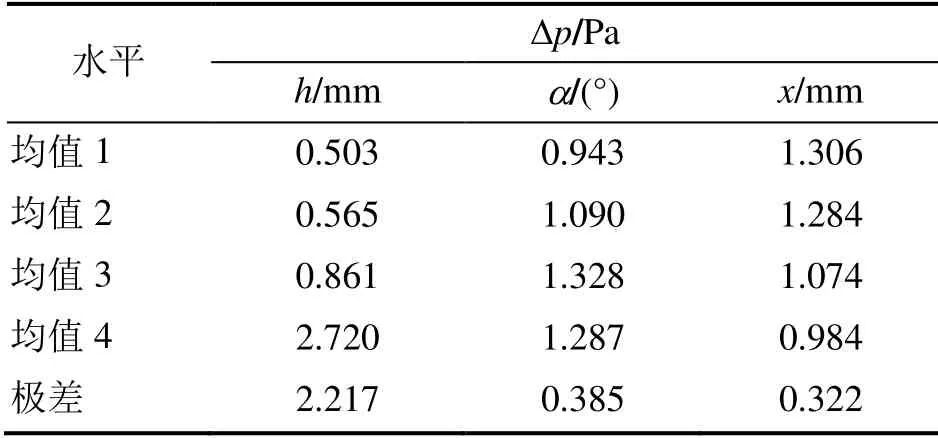
表5 压降计算结果分析

由表5可知，导流板结构参数对空气压降的影响从大到小的顺序为：导流板垂直高度h、倾斜角度α、距进风口距离x。导流板垂直高度的改变对空气流动阻力的影响最大，是空气压降的主要影响因素，导流板倾斜角度和距进风口距离对空气压降的影响程度相近，约为垂直高度影响程度的1/4。

导流板结构参数对压降的影响如图6所示。由图6可知，空气压降随导流板高度增加而增加，随倾斜角度增加先增加后降低，转折点约为90°，随距进风口距离增加而降低。因此，在实验范围内，若只考虑空气压降Δp这一目标，最优组合是高度h为5 mm，角度α为30°，距离x为120 mm，经验证，该组合下空气压降为0.47 Pa，低于上述16 组正交试验的压降。

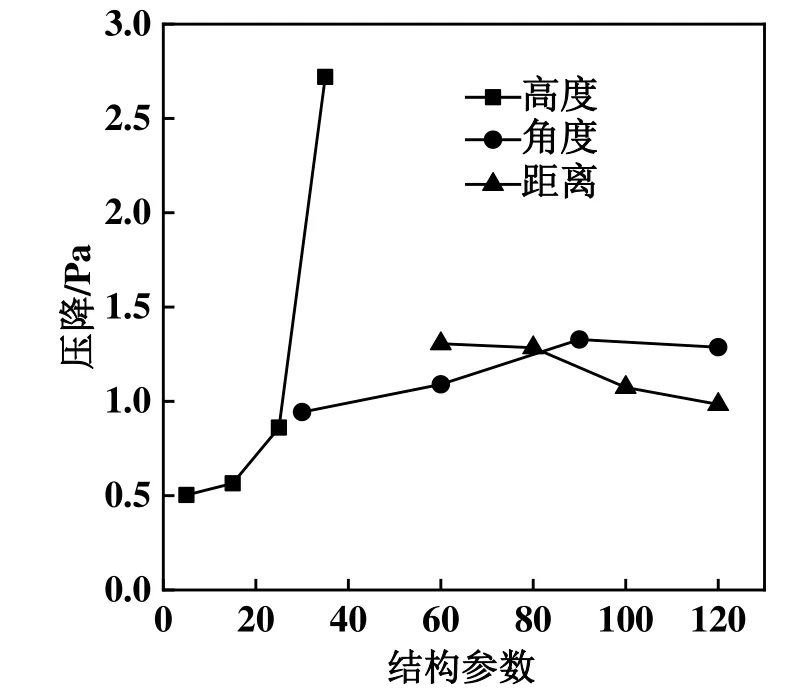
图6 导流板参数对压降的影响

3.5 结构参数对综合性能的影响

根据上述分析，可以看出以显热交换量、湿交换量或压降为单一目标得到的优化组合不一致，为研究导流板结构参数对热质交换及流动的综合影响，提出综合评价指标，用于水箱综合性能评价。根据式(9)～式(11)对目标进行归一化。

式中，A、B和C为分别为显热交换量、湿交换量和压降的归一化结果；下标max 和min 分别为通过正交试验预测的指标最大值和最小值。

根据传热传质和压降3 个目标给出综合评价指标Y，表达式为：

式中，m、n和k为分别为目标A、B和C的权重，根据实际需要可给定权重值，本文更关注结构参数对传热传质的影响，给定m、n和k值分别为0.4、0.4 和0.2。

综合评价指标Y值越大，热质交换效率越高，流动压降越低，设备综合性能越高。根据数值模拟结果，对综合评价指标进行极值分析，结果如表6所示。

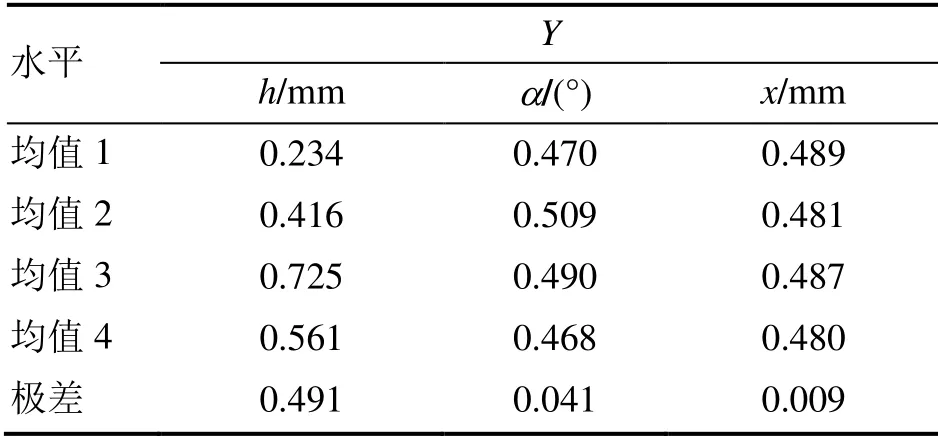
表6 综合评价指标计算结果分析

由表6可知，导流板结构参数对综合评价指标的影响程度从大到小的顺序为：导流板垂直高度h、倾斜角度α、距进风口距离x，其中导流板垂直高度对空气流动过程中传热传质和阻力平衡作用的影响最大，是综合评价指标的主要影响因素，导流板倾斜角度与距进风口距离对综合性能的影响相对较小。另外，综合评价指标随导流板垂直高度和倾斜角度的增加先增加后降低，随距进风口距离的影响受多因素耦合作用，变化规律不呈现单纯增加或降低。

综上所述，在实验范围内，最优综合性能组合为高度h为25 mm，角度α为60 °，距离x为60 mm，经验证，该组合下最高综合评价指标为0.87，高于16 组正交试验的综合评价指标。该组合的综合评价指标比以热质交换为目标的优化组合提高了0.18，比以压降为目标的优化组合提高了0.60。