基于多岛遗传算法的全封闭变流器散热结构优化
2021-03-31赵万东于博刘畅
赵万东,于博,刘畅
(珠海格力电器股份有限公司,空调设备与系统运行节能国家重点实验室,广东珠海 519000)
0 引言
变流器是一种对电能进行交直流相互转换的电能转换装置,是太阳能、风能发电系统、直流微电网、轨道交通供电、柔性输配电系统中的重要核心部件。变流器工作环境复杂多变,对高防护等级、高可靠性变流器的需求是行业发展的主要方向,高防护等级意味着变流器需采用全封闭的设计方式,以达到防水、防尘及防虫的“三防”要求,高可靠性意味着变流器需采取被动式自然对流的散热方式,以减小冷却系统故障带来的不确定性,但在全封闭的设计前提下,变流器内部元器件产生的大量热量难以及时排出,且自然对流的散热效果相对较弱,如果散热结构设计不合理,会造成变流器工作性能衰减,严重时甚至发生内部元器件过热烧毁,致使变流器永久损坏[1],因此,自然对流工况下全封闭变流器的散热结构设计非常重要。
国内外学者针对变流器散热结构设计已开展了大量研究工作。JONG 等[2]提出了采用“热管理损失密度”与“热设计等级”两项指标来评价电能转换装置热管理效率的方法,为热管理技术及方案的选择提供了全新的思路。DEVOTO[3]对变流器中功率模块的单相液冷系统进行了详细的设计,在液冷板流道中添加了塑料内插物进行换热强化,研究了内插物结构参数、制冷剂配比和热物性参数变化等因素对液冷系统散热性能的影响,结果表明,该单相液冷系统能够满足功率模块的散热需求,但未验证系统的长期可靠性。NING 等[4]采用解析法建立了SiC 变流器强制风冷散热模块的数学模型,以散热系统重量最小为设计目标,利用Matlab 编程进行寻优,获得了最优的散热器结构、风道尺寸与冷却风量,并结合仿真与测试进一步验证了优化结果的准确性,该热模型和设计方法对于强制风冷变流器散热结构设计具有普适性。
陶高周等[5]对小功率光伏逆变器自然对流散热进行了仿真建模与计算,实现了约70%的器件仿真温度误差小于3 ℃,为产品开发提供了设计依据,但文中并未阐明散热结构的设计方法。米高祥等[6]对现有大功率变流器热设计的散热需求、系统成本、散热效率和系统寿命优化等多目标进行研究,提出一种实现多目标优化的大功率变流器强制风冷热设计方案,并验证了设计方案的准确性,但文中并未考虑多个目标间的协同效应。赵红璐等[7]通过等效热路法对大功率逆变器中绝缘栅双级型晶体管(Insulated Gate Bipolar Transistor,IGBT)模块的结温以及热阻进行快速准确计算,并采用数值仿真方法对影响散热器热阻的关键参数进行了定量分析,对散热系统的散热效果进行了仿真和实验分析,证明了散热设计的准确性;张国栋等[8]根据柜体结构和功率模块的损耗,利用ICEPAK 软件结合实验测试的方法,对集中式光伏逆变器中的IGBT 模块进行了散热器设计和风机选型,仿真与测试误差控制在10%以内,验证了热设计方案的可行性和准确性。黄童毅等[9]针对具有相变冷却方式的光伏直驱冷水机组的变频器搭建实验系统,研究散热性能并优化设计,提高了变频器冷却性能及关键功率模块的温度稳定性。
综上所述,在散热冷却方式上,变流器散热结构的研究主要集中于强迫风冷与液冷散热,对自然对流全封闭变流器的散热结构设计研究较少,在散热分析对象上,大部分研究主要聚焦于局部散热模块的建模与分析,对变流器整机协同热设计的机柜级冷却方案的制定与研究较少。
本文对自然对流、高环温运行工况下的全封闭变流器散热结构进行了寻优设计,获得了最优肋片参数,为散热结构的正向设计提供了研究方法。
1 基准模型构建
1.1 研究对象
图1所示为变流器的整机构造。其箱体内部具有IGBT、功率因数校正(Power Factor Correction,PFC)电感、交流(Alternating Current,AC)滤波电感、直流(Direct current,DC)滤波电感及电容等数量众多的发热元器件,并且配备了两个循环风扇对箱体内部的空气进行搅动,促使箱体内部空气温度均匀,箱体材料为6063 铝合金,采用全封闭的结构设计达到IP65 防护等级,整机依靠铝塑箱体背面的散热肋片进行自然对流散热。
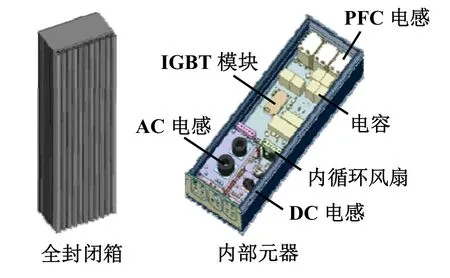
图1 变流器整机构造
变流器各元器件热损耗如表1中所示,总热损耗为429.92 W,其中IGBT 热损耗为240 W,占整机损耗的55.82%,IGBT 与PFC 电感的热损耗占到总热损耗的77.8%,经过进一步分析可知,直接贴附于箱体表面的元器件热损耗占总热损耗的86.9%,因此,散热肋片的设计对整机散热性能起决定性作用。
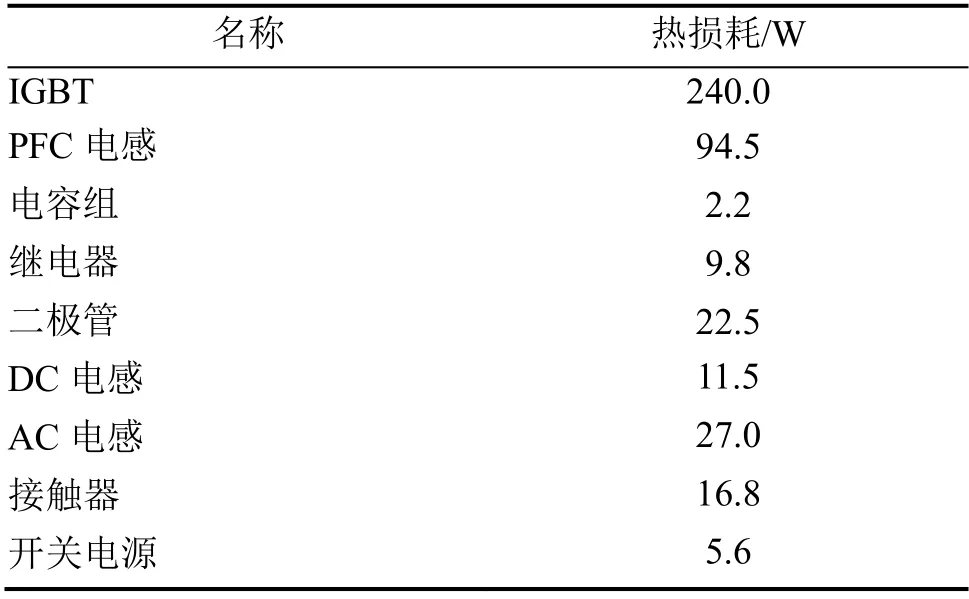
表1 变流器各元器件热损耗
1.2 模型简化与计算设置
根据整机三维构造,对模型进行适当简化,删除螺钉和连接线等细小零件,并采用六面体网格进行空间离散,网格数量达2.26×106,最低网格质量在0.25 以上。
流动方程选取方面,在自然对流工况下,需考虑重力的影响与流体密度的变化,本文研究对象属于密度变化不大的浮力流问题,WEI 等[10]认为可以只在重力项中考虑浮力的影响,而在控制方程的其它项中忽略浮力的作用,基于Boussinesq 假设,雷诺应力可表述为[12]:

式中,µt为湍流黏度,Pa·s。
采用标准k-ε模型进行流动计算:

式中,k为湍流动能,m2/s2;ε为湍流动能耗散率,m2/s3。
两个基本未知量的输运方程[12]:
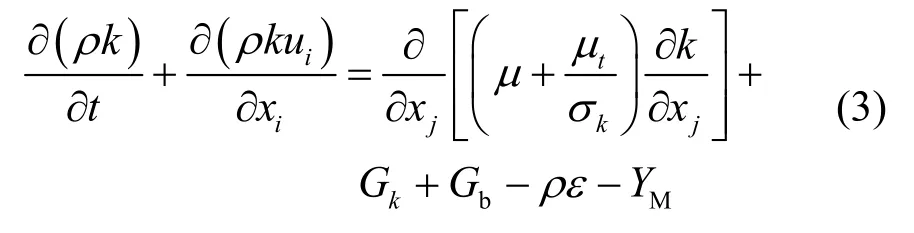
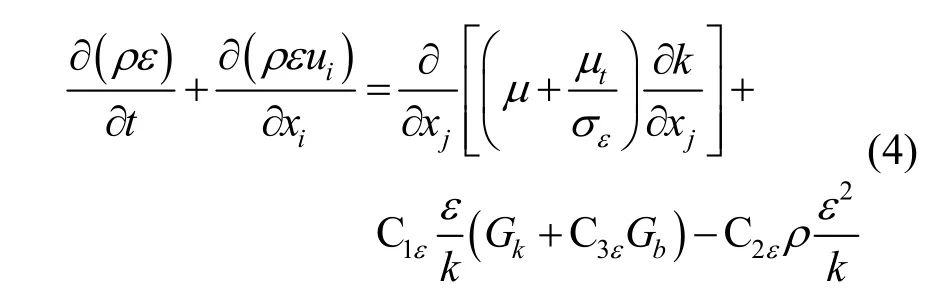
式中,C1ε、C2ε、C3ε为经验常数,σk和σε分别是与湍动能k和耗散率ε对应的普朗特数;Gb为用于浮力影响引起的湍动能产生项,对于不可压流动,Gb=0。
在标准k-ε模型中:C1ε=1.44,C2ε=1.92,C3ε=0.09,σk=1.0,σε=1.3;Gk为由于平均速度梯度引起的湍动能产生项,由式(5)计算:
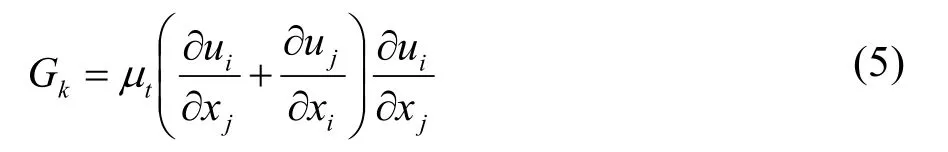
对于可压缩流动,由式(6)计算,YM为可压缩湍流脉动膨胀的贡献,对于不可压流动,YM=0。对于可压缩流动,由式(7)计算:

式中,Prt为湍动普朗特数,取0.85;gi为重力加速度在第i方向的分量,m/s2;β为热膨胀系数,1/K;Mt为湍动马赫数;a为声速。
传热计算方面,将热传导、热对流及热辐射的影响均考虑在内,主要部件导热系数设置如表2所示。由于箱体表面采用了原色阳极氧化处理,因此将发射率设为0.9,其余元器件表面发射率保持默认值0.8。
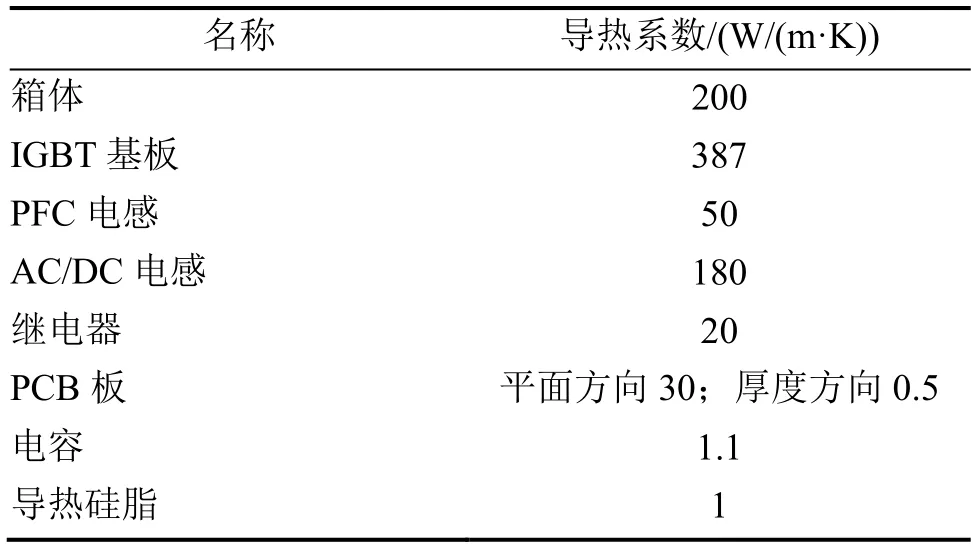
表2 导热系数设置
1.3 仿真精度验证
以现有变流器结构为基准,仿真环境温度为30 ℃时,自然对流工况下变流器内部各发热元器件温度分布情况,结果如图2所示。由图2可知,变流器内部元器件最高温度为95 ℃,位于IGBT 基板中心位置。图3所示为实验测试环境。
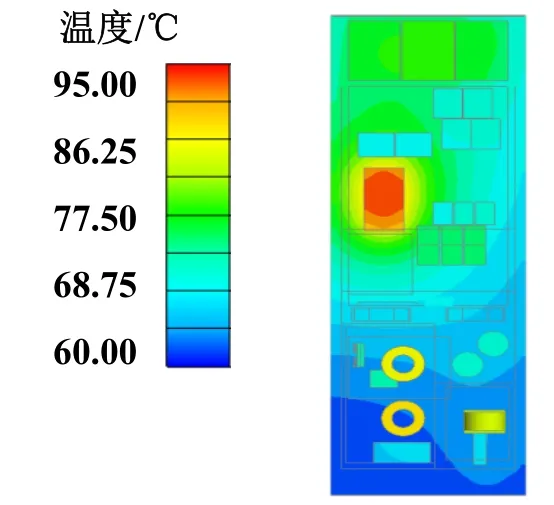
图2 仿真元器件温度云图

图3 实验测试环境
为验证仿真模型的准确性,在环境温度30 ℃的恒温环境室内进行了温升实测验证,如图4所示,变流器放置于房间正中央,周边1 m 范围内空气流速小于0.3 m/s。
温度测点选取考虑3 个方面的因素:1)关键元器件温度是否超标;2)箱体内空气温度分布是否均匀,以此判断箱体内气流组织合理性;3)热沉表面温度梯度变化情况,用于判断散热面积是否得到充分利用。因此,本次验证测试在变流器内外共布置29 个温度测点,如图4所示。按照实验测试布点读取仿真模型对应位置数据,得到仿真与测试数据对比如图5所示。

图4 测点布置情况
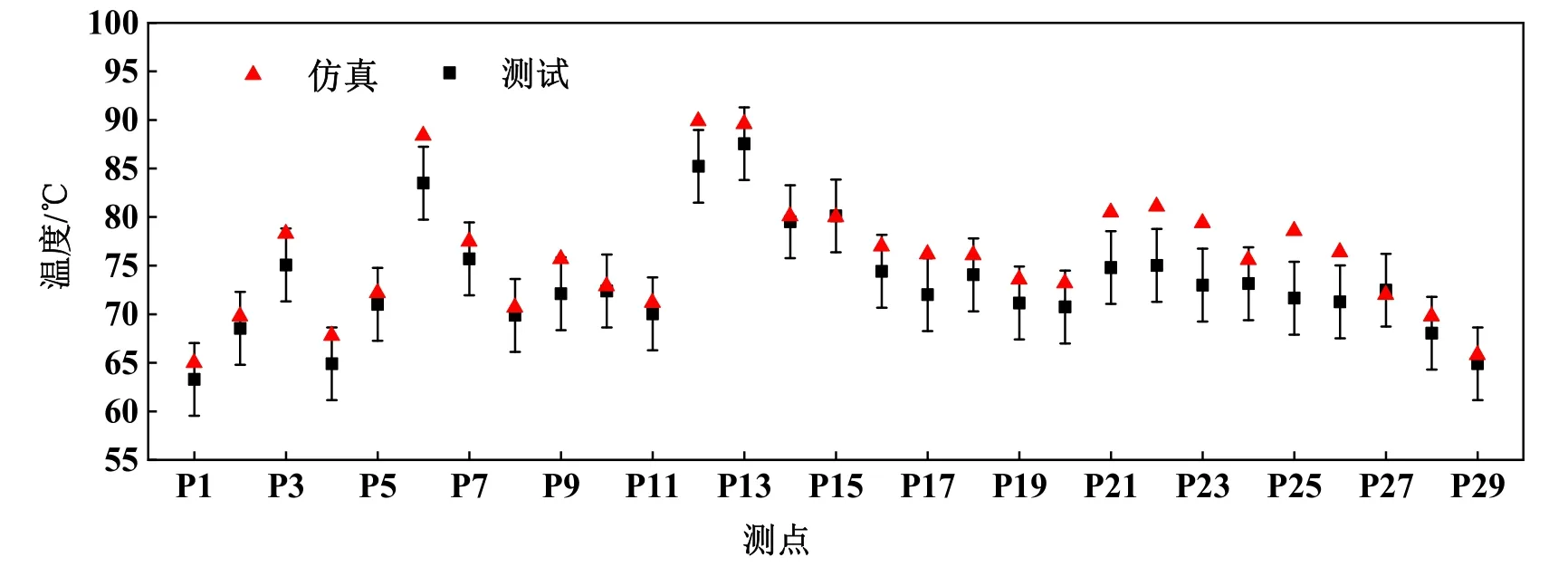
图5 仿真与测试数据对比
由以上数据对比可知,对于变流器的关键器件IGBT,仿真与测试误差仅0.4 ℃,整机29 个测点仿真与测试的标准差仅为3 ℃,实现仿真替代实验。
由仿真及测试结果可知,在30 ℃的环境温度下,IGBT 基板温度达到95 ℃,温升余量已经很小,当环境温度进一步升高时,目前的箱体结构已难以满足散热需求,因此,对散热肋片参数进行寻优设计,优化散热性能,是保障机组在高环境温度下可靠运行的关键。
2 多岛遗传算法寻优
2.1 寻优流程及理论
总体寻优流程如图6所示,选取肋片参数作为设计因子,并确定每个因子的取值范围,即形成有限个样本的样本空间;采用实验设计方法(Design of Experiment,DOE)进行样本选取,对选取出的每一个样本进行仿真计算,获得每个样本对应的温度数据,形成设计矩阵,以设计矩阵中的数据为基础,采用数学方法,拟合设计因子与响应(温度)之间的函数关系,形成近似代理模型;基于构建的近似代理模型,确定目标函数后,采用多岛遗传算法(Multi-island Genetic Algorithm,MIGA)进行全局寻优,获得最优的散热肋片结构。

图6 肋片参数寻优总体流程
在上述总体寻优流程过程中,DOE 实验设计抽样方法采用优化拉丁超立方方法,该方法可以快速得到空间填充性能和映射性能良好的任意尺寸实验样本,能够兼顾设计效率和样本性能,避免遗漏重要的样本特征[13-14]。近似代理模型构建采用四阶响应面模型进行拟合,具有精度高、计算简单、鲁棒性好、实用性强及适用范围广等优势,其数学理论模型为[15-18]:
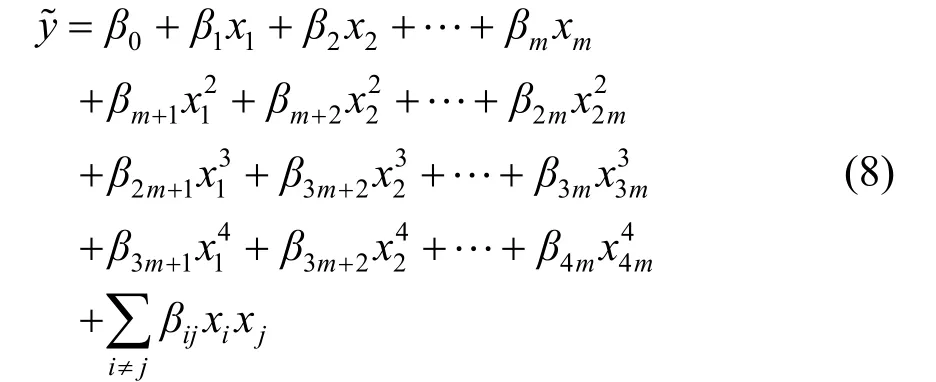
式中,β为拟合所得常数;xi、xj为不同设计因子;m为设计因子的个数;y~为响应值。
全局寻优算法采用多岛遗传算法,该算法将一个大种群分成若干个子种群,形象称之为“岛”,而在每个岛上运用传统的遗传算法进行子种群进化[19],通过反复恰当地使用遗传算法的算子和选择原则[20],从亲代到子代,从子代到孙代,从孙代到重孙代,不停繁衍,使得种群对环境的适应性不断升高。图7所示为多岛遗传算法寻优过程。假设h及n为两个不同的设计因子,在实际工程应用过程中,会存在不同的约束条件Gi,约束条件与近似代理模型共同构成了寻优空间,在该空间约束下采用多岛遗传算法进行寻优,从而获得工程上需要的最优解。与传统遗传算法相比,多岛遗传算法具有更优的全局求解能力和计算效率[21]。

图7 MIGA 寻优过程
2.2 肋片参数影响分析
选取肋片高度h、肋片厚度t及肋片间距s为设计因子(图8)。为满足工程需要,肋片高度h、肋片厚度t及肋片间距s的取值范围如表3所示。
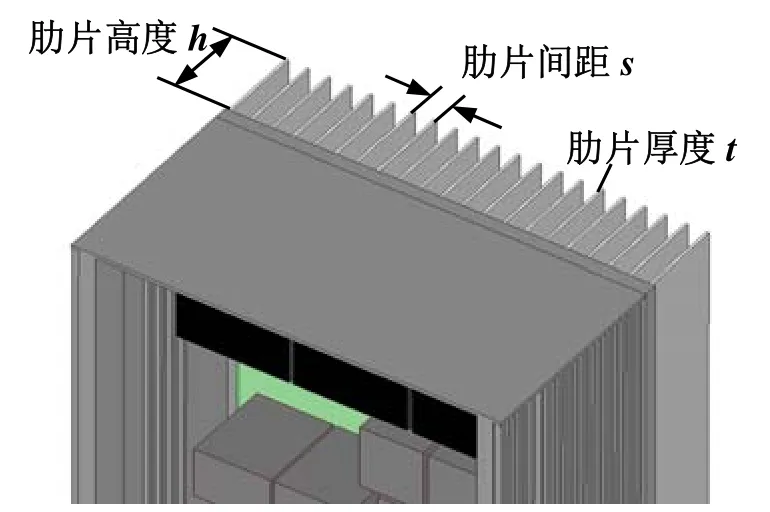
图8 肋片设计参数
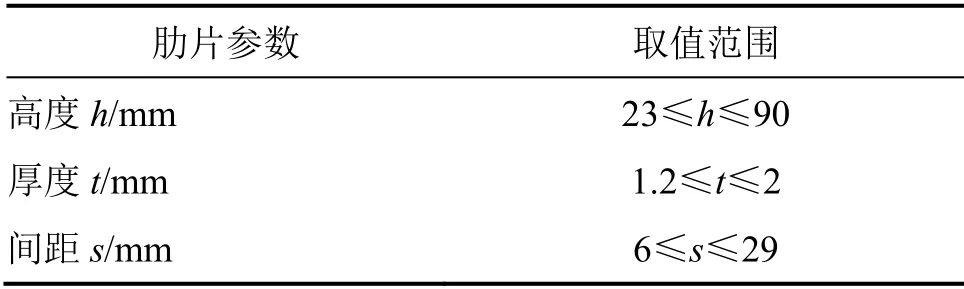
表3 肋片参数取值范围
以IGBT 基板测点P13 温度TI及变流器内部空气测点P29 温度Ta为响应值,分别构建四阶响应面模型如式(9)及式(10)所示。

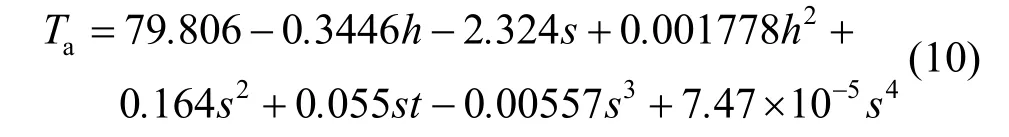
以上两式的预测精度如图9所示,对IGBT 测点温度TI的预测精度达99.68%,对变流器箱体内部空气测点温度Ta的预测精度达99.39%。
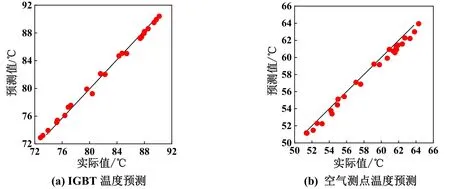
图9 近似代理模型预测精度
由图10及图11可知,肋片高度h增高时,IGBT温度与箱体内部空气温度均大幅降低,且当肋片高度h>80 mm 时,温降速率呈现放缓趋势;另一方面,随着肋片间距s的增加,IGBT 温度及箱体内部空气温度先减小后增大,约在16~19 mm 的区间内达到最优;肋片厚度t对相应测点温度几乎没有影响。
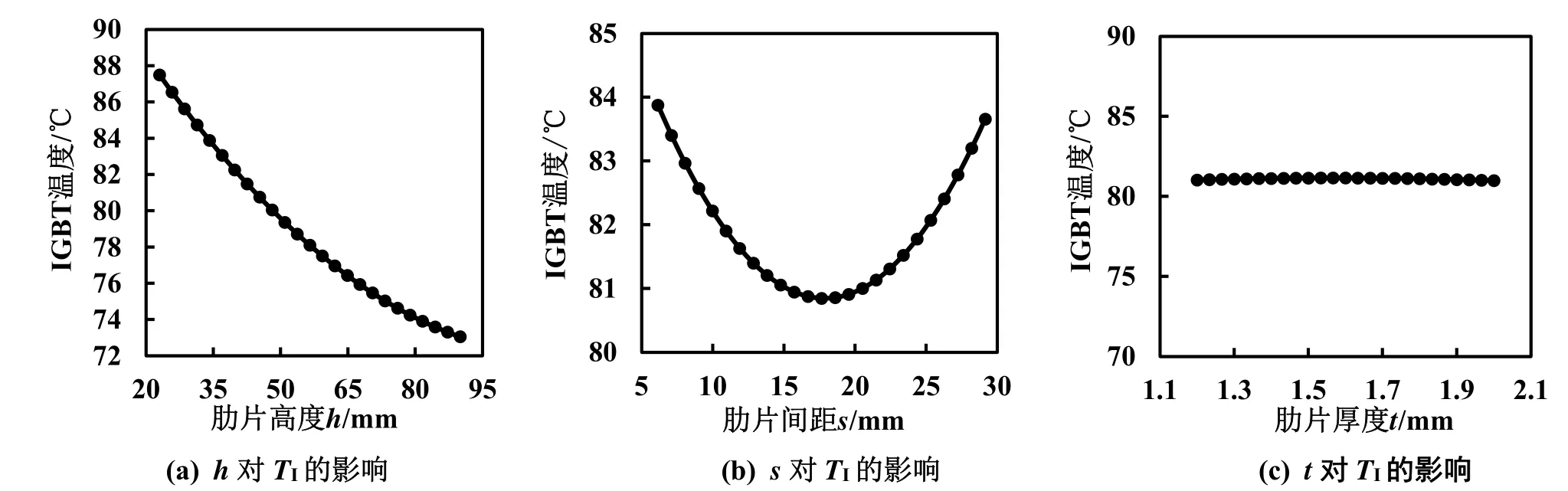
图10 肋片参数对IGBT 温度的影响

图11 肋片参数对内部空气温度的影响
为了分析各肋片参数的影响程度,对各参数的帕累托Pareto 贡献量进行分析,如图12所示。
由图12可知,肋片高度h对IGBT 测点温度及箱体内部空气温度的贡献量最大,分别达到52.82%及44.98%,且起到负效应作用,即肋片高度越高,测点温度越低;变量h、s2及h2所占贡献量达到80%以上,因此在肋片设计过程中,肋片高度及肋片间距参数至关重要。

图12 Pareto 贡献量分析
2.3 肋片参数优化
进行多岛遗传算法寻优前,制定优化目标函数如式(11)所示,即IGBT 温度与箱体内部空气温度的和最小。

为提升寻优质量,防止结果成熟前收敛,同时保证计算效率,寻优参数设置如表4所示。

表4 寻优参数设置
肋片参数优化后,IGBT 最高温度下降了18.83 ℃,箱体散热性能大幅提升,优化前后各仿真温度监测点数据对比如图13所示,可知所有测点温度均大幅下降,各测点平均温度下降15.98 ℃,为变流器在更高环温下稳定运行提供了可靠保障。

图13 各监测点温度数据对比
按表4所示最优参数构建优化后数值模型并进行仿真计算,寻优计算完成后,得到最优肋片结构参数(表5),得到30 ℃环境温度时优化前后箱体内元器件温度分布对比如图14所示。

表5 最优肋片结构参数
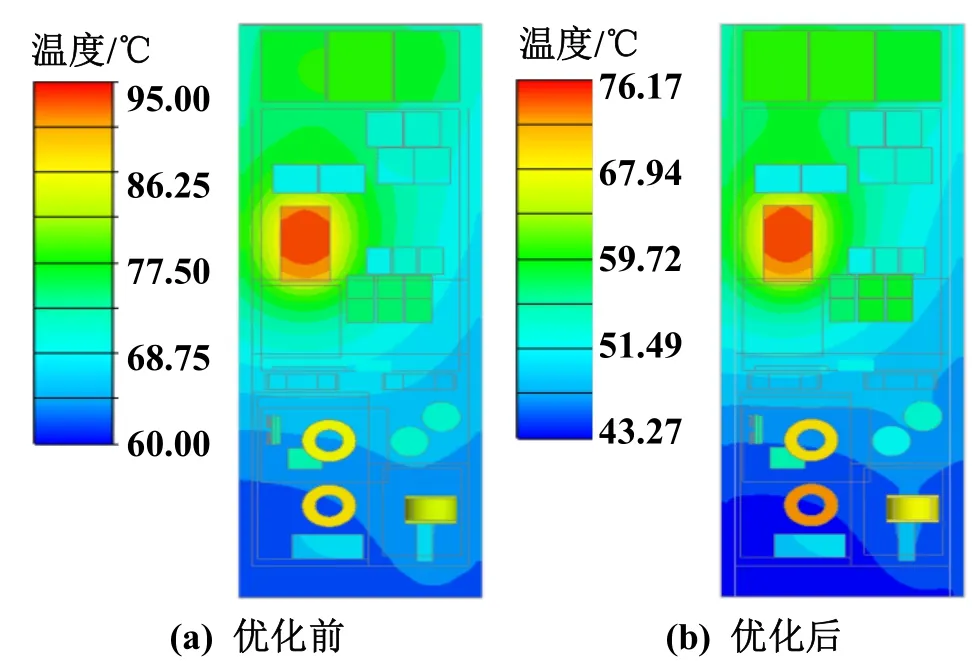
图14 优化前后温度场对比
3 结论
本文利用CFD 仿真分析与实验测试结合的方法,对变流器的散热结构进行了系统性分析,并进一步采用多岛遗传算法对肋片结构参数进行了寻优,大幅降低了变流器元器件温升,改善效果显著,得出如下结论:
1)建立了机柜级变流器散热基准仿真模型,整机各温度测点的仿真与测试标准差小于3 ℃,关键温度测点IGBT 基板温度及箱体内部空气测点温度误差小于1 ℃;
2)构建了肋片结构参数与测点温度之间的四阶响应面近似代理模型,模型精度达到99.3%以上,实现数学公式替代仿真及实验,并对肋片结构参数进行了单因素分析及Pareto 贡献量分析,结果表明肋片高度对测点温度的影响最大,其次为肋片间距,两者的贡献量达80%以上;
3)基于多岛遗传算法对散热肋片进行了寻优设计,散热肋片最优参数为肋片高度h=90 mm、肋片间距s=16 mm、肋片厚度t=2 mm,仿真计算结果表明,在30 ℃环境温度下,优化后的肋片结构使IGBT 最高温度下降18.83 ℃,变流器总体各测点平均温度下降15.98 ℃,散热性能大幅提升。
