基于微透镜阵列的交互式多公差同步分析方法

雷盼灵, 钱超义, 王 旭, 王志萍, 许雪芬

(无锡职业技术学院 基础课部,江苏 无锡 214121)

随着科技的进步,电子产品在工作生活中占据着重要的地位,其核心部件就是印刷电路板[1]。而印刷电路板制造的主流技术是光学投影曝光光刻技术,光刻机的性能即能量分配的均匀性对印刷电路板的分辨率起着决定性的作用,因此光刻机的一个关键技术即是激光整形技术[2]。激光整形技术就是将激光在空间中的能量分布进行重新分配,使其在加工的目标面上产生均匀的辐照度分布[3-4]。此外,激光整形技术还广泛地应用于激光打印、材料微加工和医疗手术等领域,激光整形的效果直接决定了仪器整体性能的优劣。

目前常用的激光整形方法有二元光学元件、液晶空间光调制器、双折射透镜组、随机相位板、自由曲面光学元件进行整形、微透镜阵列等[5-7]。其中,微透镜阵列是激光整形里面一种非常普遍的方法,其具有体积小、辐照均匀、材料方便、工艺简单、易于集成等优势[8-10]。然而,微透镜阵列系统在加工与装配中误差是不可避免的,这些误差会导致所照明目标面的均匀度和效率有所下降,因此针对微透镜阵列进行公差分析非常有必要。

现在常用的办法是人工调试某个元件的离轴,偏心等各种公差进行分析均匀度的变化,然而这些公差并非独立存在,因此分析多种公差叠加后的照度均匀度的变化及效率的变化具有重要的意义。为解决这一问题,本文构建了一个自动化的公差分析平台。该平台基于Tracepro与Matlab交互式设计,在Tracepro和Matlab之间进行动态数据交换(简称DDE),利用Tracepro强大的光线追迹能力和Matlab数据处理与分析能力,进行多公差同步分析。为使平台更便于操作,设计了交互界面。利用该平台分析了透镜阵列在三个空间轴上的距离误差、偏移误差和旋转误差以及多种公差的叠加对辐照均匀度的影响。

1 激光微透镜模型的建立

复眼透镜阵列作为一种常用的能量均匀化装置,利用复眼透镜阵列对光束进行分隔、扩散、再叠加,使光斑能量更均匀分布,如图1所示,用两排复眼透镜阵列Lens1和Lens 2实现,两排复眼透镜的间距以及各自的倾角都会影响到出射光的均匀程度[11-12]。

复眼透镜一般由N×N个矩阵排列的相同规格的矩形孔径球面子透镜组成。将两个相同的透镜阵列Lens 1和Lens 2如图1所示反方向并列放置,间距接近微透镜的焦距,使两个透镜阵列的光轴相平行,两个阵列的微透镜分别相对齐。两个透镜阵列对光束进行先分割再叠加,可实现能量均匀化[13-14]。在两个透镜阵列后并列一个会聚透镜Lens 3,将均匀化的发散光线汇聚起来。Lens 3与Lens 2的距离对光斑尺寸无明显影响[12-13]。最后放一个接收屏Screen会聚透镜的焦点上,这一接收屏可以模拟激光加工的目标面,在该目标面上期望获得最大效率的均匀光斑。辐照度均匀度U和接收效率η的定义为

其中:Emax表示目标面上最大照度值;Eav表示目标面上平均辐照度;Φs表示接收屏接收到激光总能量;Φ表示激光器发出总能量[9]。

图1 复眼透镜阵列模型结构Fig.1 Structures of microlens array

按图1所示方位,采用光学仿真软件建立一个基于微透镜阵列激光整形系统。系统中相关元件使用的参数如表1设置,透镜材料均为BK 7,参数建立的激光整形系统,经过光线追迹后接收屏获得均匀的辐照度分布,辐照度均匀度U=83.96%,接收效率η=99.62%。

表1 系统参数设置Tab.1 Parameters of the system

表2 公差类型Tab.2 Tolerances

2 多公差分析平台的构建与运行

针对图1系统中的三个透镜,考虑对称关系,一些装配公差可暂不用考虑。一般设置z轴为光轴方向,对透镜间偏移误差、距离误差以及旋转误差进行分析。偏移误差指的是透镜在y(或x) 轴方向稍微移动一定距离; 距离误差指的是透镜在z轴方向移动一定距离; 旋转误差指的是透镜绕某个轴转动一定角度。在y轴或x轴平移单个透镜造成的偏移误差影响相同,所以本文只考虑某个透镜在y轴上的偏移误差; 沿x轴或y轴旋转单个透镜的旋转误差效果可类比,所以本文只考虑某个透镜在x轴上的旋转误差; Lens 3在z轴旋转对光斑无明显影响,故无须考虑。此外,还需要考虑在z轴平移单个透镜造成的距离误差。最终对应的部分公差如表2所示,需要分析的单项公差共11处。

通过使用Matlab和Tracepro进行交互式分析,一个多公差分析平台被搭建。在平台中,可使用Tracepro宏语言进行公差模拟和光线追迹,而Matlab将对结果进行数据分析后画出辐照度均匀性和接收效率的变化曲线。Matlab和Tracepro之间的数据交互通过动态数据交换(DDE)协议来完成[15]。

整个平台运行过程中,Matlab的具体流程如图2所示,运行程序后储存数据到指定路径,并将数据绘图储存,以备Matlab制作图形用户界面(GUI)时调用[16]。

图2 程序流程图Fig.2 Flow chart of the whole program

利用Matlab制作图形的用户界面如图3所示,可将对应自由度的相关参数表示在界面上。包括透镜的选择、透镜移动或旋转方向的选择、透镜移动距离或旋转角度以及相关参数变化的范围和步长,都可以直接在界面中设置。点击效率或均匀度按钮,即可根据输入的参数实现追光,并在计算结束后调用数据图片显示到界面上,使公差分析更即时、便捷、直观。

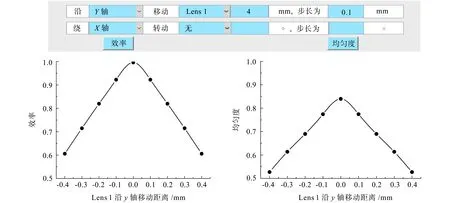
图3 用户界面设计Fig.3 Design of user interface

3 结果分析

在复眼透镜装配公差的分析中,由于模型具有对称性,只需研究表2中Lens 1对应的4处公差,即可得到相关装配公差对光斑的影响。利用前述平台,在一定公差范围内按一定步长变化进行连续追光,即可获得相应的平均照度、效率和均匀度等信息。

3.1 仿真结果

对Lens 1的计算结果,主要包括以下几方面。

(1) 在y轴(或x轴)方向微微移动Lens 1的偏移误差的影响。因为微透镜底部空间周期为1 mm,所以取偏移范围接近 1mm。公差范围取-0.45～0.45 mm,步长为0.1 mm。计算结果如图4所示。可以看到在y轴方向无偏移时,效率和均匀度效果都是最佳的。可看出,y轴(或x轴)偏移误差在±0.1 mm及以内,均匀度的降低在10%范围内(即不低于73.96%)。

(2) 只在z轴方向微微移动Lens 1的距离误差的影响。只有Lens 1和Lens 2间距接近焦距即z轴坐标为0时,光斑的效率和均匀度都处于比较理想的状态,如图5所示。如果偏离焦距较远,则效率和均匀度两者必有一个会出现较明显的下降。可看出,z轴偏移误差在-0.2 mm及以上,均匀度的降低在10%范围内。

图4 Lens 1沿y轴偏移时对光斑效率以及均匀度的影响 图5 Lens 1沿z轴移动时对光斑效率以及均匀度的影响 Fig.4 Effects on efficiency and uniformity as Fig.5 Effects on efficiency and uniformity as Lens 1 moves along y axis Lens 1 moves along z axis

(3) 分别将Lens 1绕着z轴和x轴微微旋转的旋转误差的影响。实际旋转时可顺时针或逆时针旋转,计算时可只选择特定的顺时针方向。图6显示了Lens 1绕光轴z轴旋转一定角度后的光束的效果,此时Lens 1和Lens 2的光轴仍然是平行的。图7显示了Lens 1沿x轴旋转的结果,此时Lens 1和Lens 2的光轴不再平行。

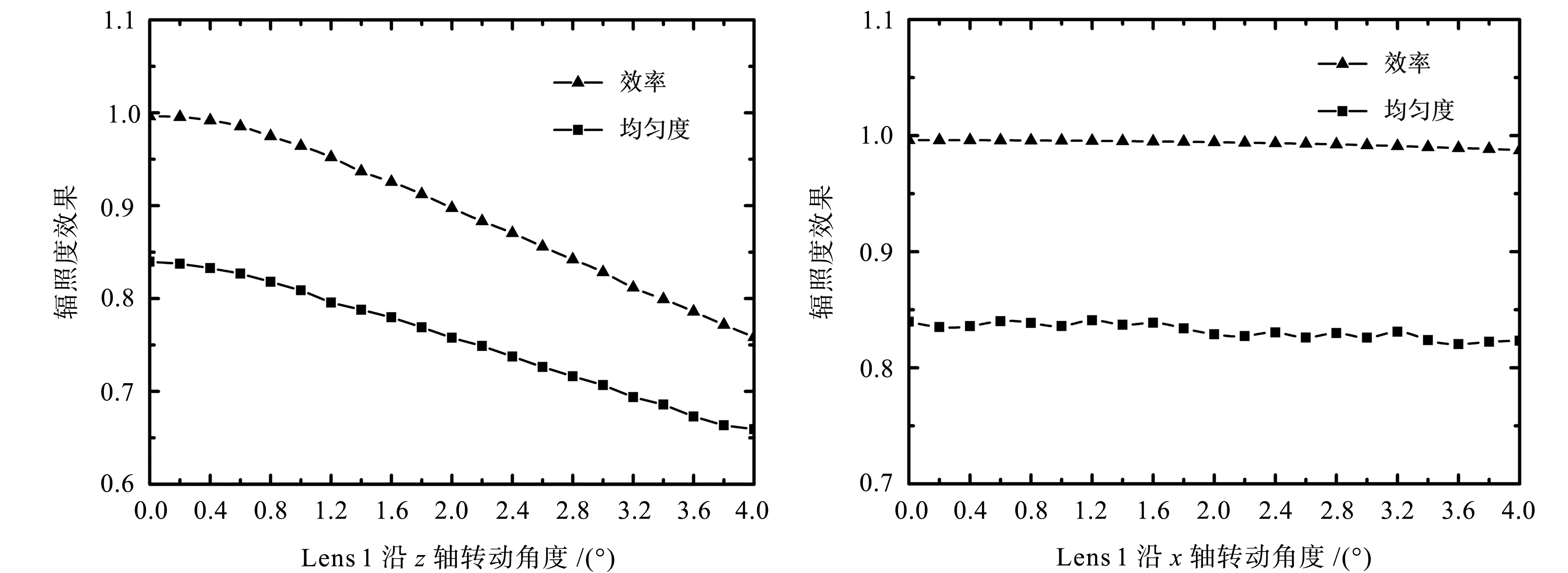
图6 Lens 1绕z轴旋转时对光斑效率以及均匀度的影响 图7 Lens 1绕x轴旋转对光斑效率以及均匀度的影响 Fig.6 Effects on efficiency and uniformity as Fig.5 Effects on efficiency and uniformity as Lens 1 moves along z axis Lens 1 moves along x axis

对比可以看到,沿着z轴的旋转对于光斑的影响很明显。旋转之前,原先Lens 1的一个微透镜正对Lens 2的一个微透镜(底面积为正方形); 偏转后一个Lens 1微透镜的出射光将会分布到Lens 2几个临近的微透镜上。这会降低光斑的均匀度,且边界的反射散射造成效率的明显下降。沿x轴旋转同样也会降低均匀度和效率,但影响较小。从图7可看出,均匀度和效率随着Lens 1绕x轴的旋转几乎没有降低。这是因为微透镜沿着x轴方向旋转,正是让光线沿着微透镜正方形底面的某边长方向偏移,微透镜边界的反射散射相对不明显。Lens 1绕z轴旋转2.2°及以内,或绕x轴旋转4.0°及以内,均匀度的降低都在10%范围内。

(4) 偏移误差和距离误差的同时影响。由于实际装配情况复杂,可能同时存在多种公差。假设Lens 1沿着y轴和z轴同时有移动量,仿真得到光斑的效果如图8和图9所示。可以看到,y轴方向的偏移由于微透镜自身尺寸空间周期的存在,光斑在同样的周期上有效率和均匀度的周期变化,周期内变化符合图4所示;z轴方向的移动效果与图5结果吻合。此外,比较其他多种公差同时存在的影响,并未发现多种公差反而相互消除影响的作用。也即y轴(或x轴)偏移误差在±0.1 mm及以内,或者z轴偏移误差在[-0.2,0.4] mm范围,或者绕z轴旋转2°及以内,或者绕x轴旋转4.0°及以内,达到效率和均匀度不能降低超过10%的要求。同时,图8和图9也分别表明,如果只是单独追求效率或者均匀度,实际装配时偏移误差和距离误差的要求会降低很多。

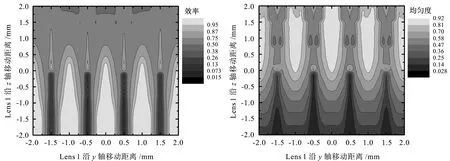
图8 Lens 1沿x轴和z轴移动时对光斑效率的影响 图9 Lens 1沿x轴和z轴移动时对光斑均匀度的影响 Fig.8 Effects on efficiency as Lens 1 moves Fig.9 Effects on uniformity as Lens 1 moves along both x and z axis along both x and z axis

3.2 实际案例应用

在激光器光束匀化系统的光学设计中,常采用如图10所示的结构。半导体激光器发出激光,通过激光整形系统对激光的能量重新分配后,均匀地照到工件台上,对工件进行加工。

图10 复眼透镜阵列应用示例图Fig.10 Example of microlens array in application

针对激光整形系统中左一复眼透镜Lens 1,进一步减小平移步长为0.01 mm、旋转步长为0.1°,进行仿真,提高偏差精度,可得到不同的均匀度要求所对应偏差范围如表3所示。其中,在x或y轴平移正负值范围内满足均匀度要求,在z轴平移正方向时均满足要求,负方向一定值以上满足要求,绕x、y或z轴旋转正负值范围内满足要求,绕x或y轴旋转的影响最小,在x或y轴平移的影响最大。对于表3偏差范围精度,目前的装配技术已经可以达到,此结果可用于装配指导。

表3 不同均匀度对偏差范围的要求Tab.3 Deviation requirements for different uniformity

4 结论

通过利用Matlab和Tracrpro的交互,创建了一个多公差同步分析平台,并对微透镜阵列进行多公差同步分析,模拟了装配公差对出光效率和均匀度的影响。模拟结果表明: 复眼透镜阵列Lens 1在y轴(或x轴)上移动时,对均匀化效果和效率均有影响; 在z轴上正向或反向移动时,对光斑均匀度和效率的影响程度不同,但仍是比较明显的影响; 绕y轴(或x轴)旋转时,对均匀度影响较小; 绕光轴方向z轴旋转时,对均匀度的影响比较明显。当多种公差叠加时,并未能减小对均匀度的影响。但同时获取多种公差的影响对装配有一定指导意义,可以获得在一定效率和均匀度允许范围内时均可容忍的公差范围。同时,该交互式多公差分析平台可以扩展至包括装配误差、厚度误差、边缘误差、表面误差和折射率等在内的所有公差分析。