基于多自由度解耦方程的系泊系统分析—吃水深度模型
2021-03-31王帅
洛阳师范学院学报 2021年2期
王 帅
(长春光华学院 基础教研部,吉林 长春 130033)
1 简述
从海域的实际状况出发,考虑海水速度及风速等因素建立数学模型.
在分段外推法的系泊系统分析倾斜角度模型的基础上,运用其所建立的模型,求出风速为36 m/s时钢管和钢筒的倾斜程度、锚链形状和浮标游动区域. 然后进行分析,从而得出重物球质量范围.
2 符号假设与约定
各种符号含义与约定见表1.

表1 符号约定
3 浮标吃水深度模型
在浮标与水平面交汇处,以圆面中心为原点,建立空间直角坐标系(图1).
设浮心坐标为(x1,y1,z1),则计算公式为
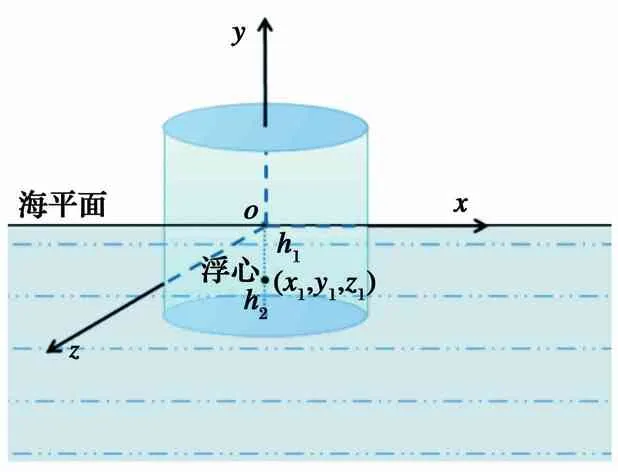
图1 浮标空间直角坐标系
设此时浮标排水体积为V,排水质量为M,则
V=V1+V2,M=ρV(ρ为海水密度)
其中h1为浮心到水面的距离,h2为浮心到浮标底面的距离,吃水深度h=h1+h2.
下面利用浮标吃水深度的求解模型来解出风速为36 m/s时钢筒和各节钢管的倾斜角度,锚链形状和浮标游动区域.
根据浮标受力的平衡分析可知,该锚链呈悬曲线形状,此时有
根据公式可知,锚点与海床的夹角φ愈大,则重物球质量就越小,此时钢筒的倾斜角就越大. 用逐步近似法求出使钢筒倾斜角不超过5°,锚链与海床夹角不超过16°的重物球重力范围(图2).
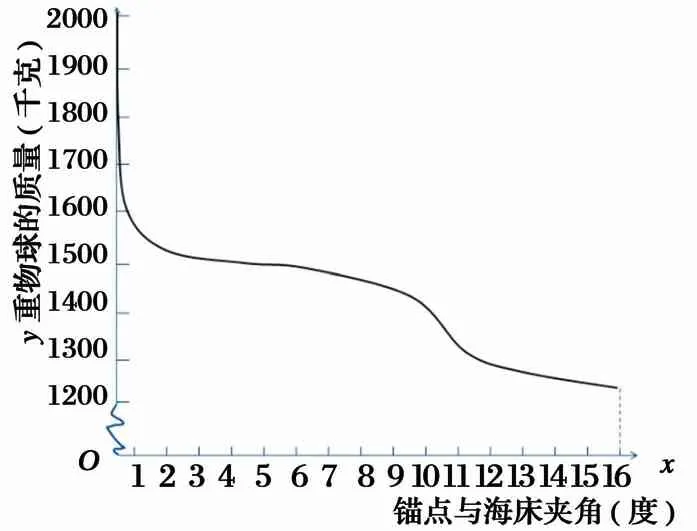
图2 重物球质量变化图
4 求解吃水深度
V=V1+V2,M=ρV=ρ(V1+V2)
(ρ为海水密度),而浮心位置纵坐标
整理得
代入数据解得吃水深度h=h1+h2=0.164 m


表2 模型求解结果
