一种新型空间权重矩阵及其在省域碳排放中的应用

李 翼，桂预风

(1.淮北师范大学 数学科学学院，安徽 淮北 235000； 2.武汉理工大学 理学院，湖北 武汉 430070)

0 引言

改革开放以来，国民经济的不断攀升也导致了二氧化碳排放量不断增加，目前研究经济增长与碳排放关系的方法有因素分解法、多元线性回归法、空间计量模型分析，而空间面板模型法因为考虑空间因素而受到越来越多的学者的青睐. Grossmanc(格罗斯曼)和Krueger[1](克鲁格)(1995)提出的“环境库兹涅茨曲线假说”(EKC)及环境污染会随着经济增长先增长后衰减. 陈操操等[2]通过空间计量模型对京津冀地区的碳排放数据进行实证分析，认为经济增长与我国碳排放正相关，且区域碳排放扩张严重； 许连和、邓玉萍[3]采用空间计量模型研究表明，在地理上的集聚有利于我国的环境改善； 姚奕、倪勤[4]利用空间面板计量模型分析了外国直接投资(FDI)对碳强度的影响，认为FDI对于改善碳排放大有裨益.

自Paelinck(帕林克)首次提出空间计量经济学以来，空间计量经济学及其模型广受学者的喜爱，被应用到众多场景. 而空间计量经济学最大的亮点在于引入了区域间的空间相关因素，而空间权重矩阵正是这种因素的表现形式，因此如何构造合理的空间权重矩阵直接关系到模型的效果和实证结果. 传统的空间权重矩阵有基于邻近关系的空间权重矩阵，相邻为1，否则为0； 但是随着空间计量经济学的不断发展和研究范围的拓展，简单的地理0-1空间权重矩阵已经不能满足研究的需要. 在后来的研究中，林光平等[5](2006)引入GDP指标，提出了经济空间权重矩阵，避免了仅考虑地理因素所遇到的问题. Aldstadt(奥尔德施塔特)等[6]提出新的思路，基于局域统计指数，考虑网络模型的结构复杂性，使用网络搜索空间自相关性构建空间权重矩阵. Kostov 利用[7]Componentwise-Boosting(CWB)方法将空间权重矩阵的设定转化为变量选择. 王君婕、张宁[8]认为区域协动效应对地区之间的经济往来有着重要影响. 李立等[9]认为挖掘区域经济指标尤为重要，综合地理因素和经济状态指标构造的权重矩阵具有更好的适应性. 由以上可以看出，空间权重矩阵的构造多种多样，学者们在构造空间权重矩阵时尽可能考虑地区之间的各种指标之间的联系，通过多种方法刻画地区之间的经济引力，力图使空间权重矩阵的合理性和优越性更明显.

本文在前人的基础上，提出了灰色引力空间权重矩阵构造方法； 通过LASSO算法筛选出与碳排放相关的经济指标，并利用灰色关联度刻画了指标所反映的各地区的经济距离与地理信息. 结合两种矩阵构造出灰色引力空间权重矩阵. 通过2010—2018年全国30个省份(不含港澳台和西藏)相关指标的面板数据，构造出新型空间权重矩阵，并基于空间计量模型进行建模分析.

1 研究方法和数据来源

1.1 碳排放计算方法

由于缺少CO2排放的直接监测数据，已有的研究一般采用能源的消耗量来估算CO2排放量. 本文参考《国家温室气体清单指南》第二卷(能源)第六章提供的计算方法估算CO2的排放总量，选取原煤、焦炭等7种最主要的化石燃料，根据每种燃料所排放的二氧化碳总量累加得到我国碳排放的总量.

(1)

其中Carbon为需要计算的CO2排放总量，E表示各种能源的消费总量，ω代表各种能源的二氧化碳排放系数，本文使用的是国家发改委在《中国应对气候变化国家方案》中提出的二氧化碳排放系数(表1).

表1 不同能源二氧化碳排放系数

1.2 空间计量经济模型

空间计量模型起源于空间统计学和区域经济学，旨在在传统的计量经济学方法下，另外充分考虑空间影响因素. 空间回归模型的特别之处，在于通过反映地区空间效应的矩阵W修正一般线性回归模型. 根据矩阵在模型中不同的表现形式，可以将模型分成两种：

1)空间滞后模型(SLM):

Y=ρWY+Xβ+ε
ε～N(0,σIn)

(2)

2)空间误差模型(SEM):

Y=Xβ+μ
μ=λWμ+ε
ε～N(0,σIn)

(3)

其中Y为因变量，X为自变量矩阵，β为待估参数向量，ε表示为随机误差项，W代表反映着地区关系的空间权重矩阵.

2 灰色引力空间权重矩阵的构造

空间权重矩阵作为空间效应的载体是地区空间效应的具体体现，因此国内外学者对空间权重矩阵的构造尤为关注. 简单考虑地理因素或者经济因素已经不能满足空间建模的需要，本文提出综合经济和地理因素的灰色引力空间权重矩阵，其构造如下.

W=W1.*WG

其中W1为普通的0,1邻近空间权重矩阵：

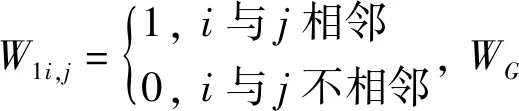
地理学第一定律表明：区域间的任何事物都具有一定的联系性，事物之间的距离越近，其联系度会越大，反之，事物之间的联系度会越小.WG在考虑地理学第一定律的基础上构造为

(4)

综合相关文献，找出前人研究的与碳排放相关的各类指标，保证指标的全面性； 为防止指标之间可能出现的多重共线性问题，筛选出与因变量关系最为密切的自变量指标. 本文通过LASSO算法检验并筛选相关指标，保证了后续建模的精度和说服力.

LASSO算法[10]由Robert Tibshirani(罗伯特·提比希拉尼)于1996年提出，此方法通过限制构造出的模型的绝对值系数函数，进而压缩模型系数，以达到模型的特征筛选工作. 考虑现有的多元线性模型：

(5)

设每个指标彼此相互独立，或者希望的因变量LASSOYi在观测值给定的情况下独立，即Yi关于xij条件独立，同时假设xijLASSO是标准化的，则LASSO估计为

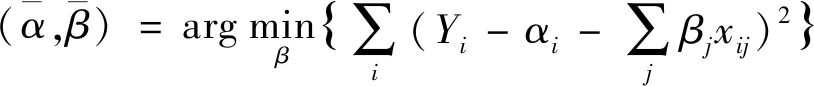
(6)

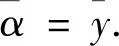
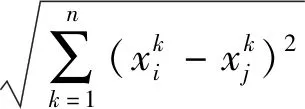
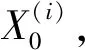
(7)

εi(k)=

(8)

(3)计算灰色关联度.

对于分子项的mi，借鉴李立等[9]构造的方法，令mi表示第i个地区在所选时间内的吸引投资的能力. 本文以不同经济体在该年度的社会固定投资总额表示地区的投资吸引力.

得到W1和WG后，点乘表示地理位置的W1和体现经济关联的WG，并进行标准化后得到最终的灰色引力空间权重矩阵W.

3 我国碳排放空间差异的实证分析

3.1 样本数据和基于LASSO回归的指标筛选

本文采用2010—2018年度我国30个省份(港、澳、台、西藏除外)碳排放相关指标的面板数据，其中计算二氧化碳排放的各类能源数据来自2019年《中国能源统计年鉴》.

综合前人的研究成果发现，二氧化碳排放与技术水平、能源结构、经济、人口、绿化等很多因素相关，因此在自变量的选择上，本文首先选取X1：年末人口总量(P)；X2:人均GDP；X3:各省份城镇化水平(UR)；X4：能源强度(EI)；X5:对外开放程度(TR)；X6:产业结构(IS)；X7:外商投资(FDI). 其中为了消除人口因素带来的影响，故采用人均GDP衡量地区经济指标； 能源强度为能源消费量/GDP，即单位经济的能源消费水平； 城镇化率为年末城镇人口/年末总人口； 产业结构用第二产业/GDP的比重来表示; 对外开放程度用对外贸易出口/GDP来表示。 除了以上常见的指标之外，本文还选取X8:工业排放强度(DI)表示一个地区工业的污染情况，在此本文选择工业污染治理额来表示；X9:城市绿化水平(SL)，用地区林业用地面积表示. 以上各指标均来自2011—2019年《中国统计年鉴》，部分指标来各省份的统计年鉴.

由于R语言有关于LASSO回归的建模包，对各自变量进行逐步加入并通过cp值对模型各自变量进行筛选. 因此本文在进行LASSO回归建模时，利用R语言lars函数对以上自变量指标进行筛选，来剔除多重共线性的影响. 建模结果如表2.

表2 LASSO回归结果

由表2可以看出，随着模型逐渐加入当前条件下的最优自变量，模型整体的cp值越来越低，而当模型加入自变量X9(城市绿化水平)时，此时模型的cp值达到最小值，表示此时的模型为建模的最佳模型. 观察模型结果，最优模型中剔除了X6(产业结构)和X7(外商投资)两个自变量指标.X6(产业结构)被剔除，可能是因为与选取的工业污染治理有部分重复； 而对外贸易已经反映了X7(外商投资)，所以其也被剔除.

3.2 空间相关性检验

3.2.1 全域空间自相关分析

全域空间自相关分析，是一种可以较为准确地衡量各个单元区域的整体因变量分布的空间差异程度及空间关联关系的分析方法.

常用的全域空间自相关是Moran’sI指数，Moran’sI指数定义如下

(9)

其中n表示空间各个单元数目的总和；yi和yj分别表示区域i和j的具体指标大小；wij为空间权重矩阵中区域i和j的空间关系大小，表示各空间单元邻近关系. 分别对比地理0-1空间权重矩阵和本文构造的空间权重矩阵得到不同权重矩阵下的Moran’sI指数值(表3).

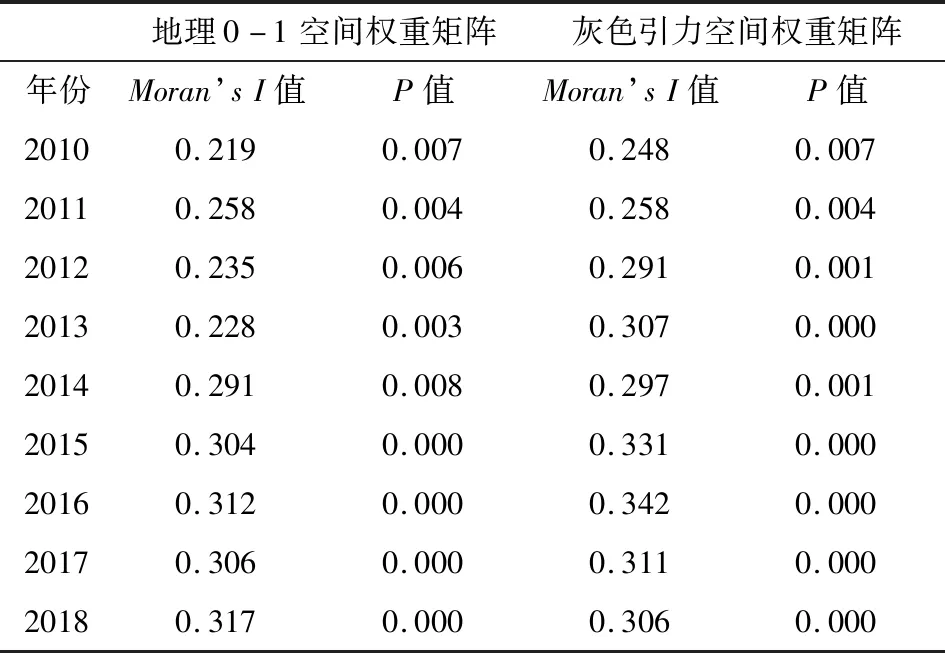
表3 各年度两种空间权重矩阵Moran’s I指数值对比

由表3可以看出：各年份碳排放的Moran’sI值均通过0.01的显著性检验. 这说明我国碳排放呈现较为明显的空间聚集效应，采用普通的面板模型无法准确地反映出我国碳排放的特征，必须采用空间面板模型对数据进行建模.

基于本文构造的空间权重矩阵，其空间自相关检验的莫兰值要略高于0-1空间权重矩阵的莫兰值，说明本文的灰色引力空间权重矩阵可以更好地反映我国碳排放的空间聚集效应.

接着对我国2010—2018年的碳排放空间面板模型，进行面板模型的空间自相关检验、LM检验以及Hausman检验. 此外，本文还对空间权重矩阵进行矩阵分块处理，将其扩充到面板形式，可以得到空间面板模型的Moran’sI值(表4).

从表4可以看出，针对所构造模型的空间自相关检验中，碳排放的空间聚集效应依然明显. 对于两种空间权重矩阵，面板模型的LMERR比LMLAG要显著，而且R-LMERR相对于R-LMLAG同样显著. 所以对于模型选择来说空间误差模型(SEM)比空间自回归模型更适合本文的研究.

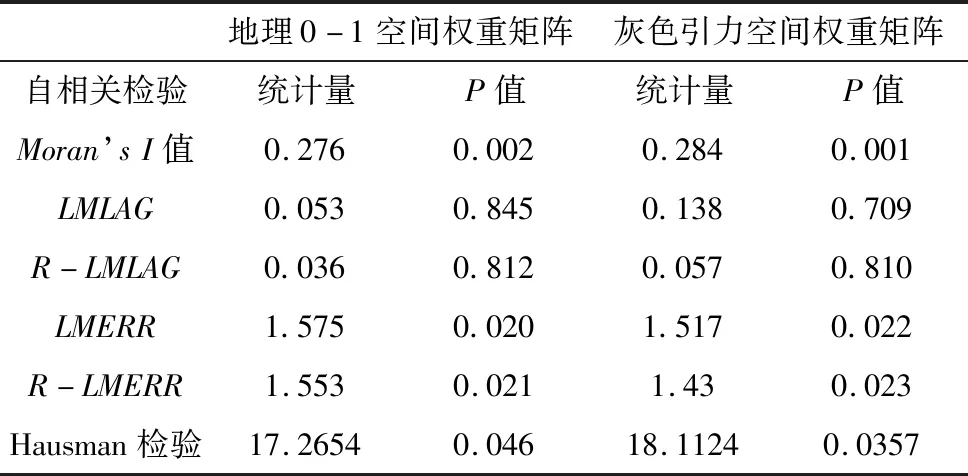
表4 两种矩阵各指标对比

本文选用空间固定效应SEM模型进行研究，原因如下：1)从Hausman检验可以看出，Hausman检验统计量通过了水平为5%的显著性检验，从而采用固定效应模型进行研究较为合理. 2)本文的地区数远大于时间数，采用空间固定效应的SEM模型较为合理，如果同时考虑模型的时间效应会导致模型的自由度过大，显著性检验将失去意义. 因此，本文采用空间固定效应模型对比两种矩阵，对碳排放进行建模分析.

3.2.2 我国碳排放的模型设定

对于碳排放的研究，绝大多数学者采用基于环境库兹涅茨曲线的研究. 结合前人的研究，本文SEM模型设定如下：

C=α0+α1lnPGDPit+α2ln2PGDPit+

α3ln3PGDPit+α4lnXit+εit

εit=λWεit+μit

(10)

其中C为二氧化碳排放总量；PGDP为人均经济发展水平及生产总值；X为通过LASSO算法筛选的各种控制指标;μit是随机误差项;λ为空间误差系数，度量了周边省域碳排放对本省碳排放的影响力大小. 若α1<0,α2>0且α3>0，以横坐标表示经济增长，纵坐标表示环境污染，那么曲线形状为“倒N形”； 若α1>0，α2<0且α3>0，则曲线将呈现“N形”； 若α3=0，此时曲线可能是“倒U形”或“正U形”.

接着对空间误差模型进行参数估计，对于空间模型的估计，在参数估计时，普通最小二乘法会导致估计的参数无效或者有偏，所以需要用其他估计方法，如工具变量法、广义最小二乘法以及极大似然法等，本文采用极大似然估计方法来估计模型的参数[12].

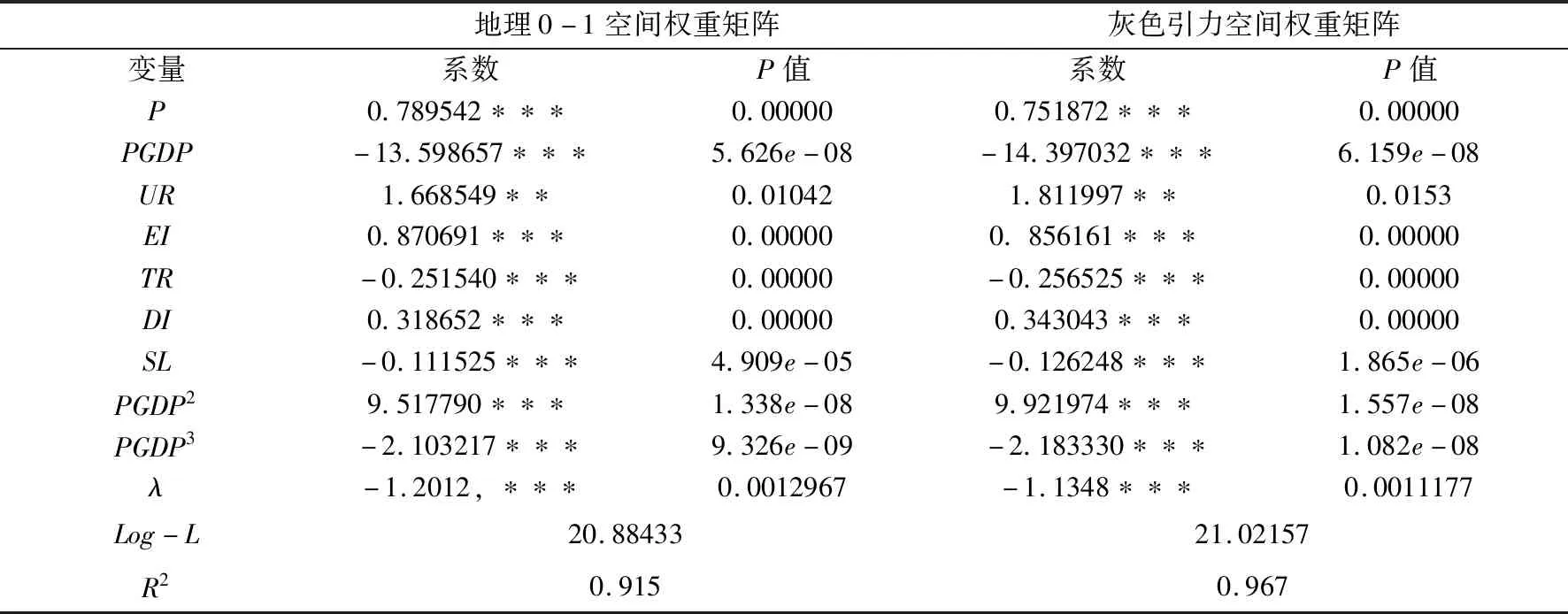
表5 模型估计结果

从表5可以看出，PGDP一次方系数、二次方系数以及三次方系数分别为负、正、负，说明我国碳排放库兹涅茨曲线形式呈现出“倒N形”. 这说明目前我国碳排放的模式为，随着经济的发展先减少后增加最后再减少. 各项指标绝大多数通过1%的显著性检验，部分通过5%的显著性检验. 城镇化、能源强度、工业排放强度系数为正，说明城镇化的进程、能源强度的提高以及工业排放强度的提高都会增加二氧化碳的排放； 而对外开放水平以及城市绿化是降低我国碳排放的有效手段. 对比两种空间权重矩阵，灰色引力空间权重矩阵不仅空间自相关性检验要优于地理邻近空间权重矩阵，而且在模型拟合上，基于本文构造的空间权重矩阵模型拟合效果更好，体现了该矩阵构造方法的有效性和可行性.

4 结论

我国碳排放呈现出较为明显的空间聚集效应，经实证发现我国碳排放环境库兹涅茨曲线呈现出“倒N形”，表明我国碳排放会随着经济的发展先降低再提高最后再降低； 基于LASSO算法筛选自变量指标保证了建模的合理性和准确性； 本文构造的空间权重矩阵不仅能更好地反映地区之间空间自相关效应，而且对于模型拟合效果也有一定程度的提高，体现了方法的有效性和可行性.