一种结合边缘检测的多基线InSAR高程反演方法

梁小星，谢先明，孙玉铮

(桂林电子科技大学，广西 桂林 541004)

0 引言

干涉合成孔径雷达(synthetic aperture radar interferometry，InSAR)可以高精度、高可靠性地获取地表三维信息和高程变化信息，被广泛应用于海洋监控、火山监测、地震检测和数字高程重建等领域。传统的单通道InSAR高程反演技术受限于Itoh相位连续性假设，通常难以有效获取不连续地形干涉图的真实高程信息[1]。鉴于此，多种不受Itoh相位连续性条件限制的多基线InSAR高程反演技术被相继提出。文献[2-3]提出了基于中国余数定理(chinese remainder theorem，CRT)的多基线InSAR高程反演技术，用多幅基线满足两两互质的干涉图构建同余方程组，利用CRT求得唯一解，能有效克服相位模糊的问题，可从理想状态的无噪声干涉图中获取精确的地形高程信息。Yuan等[4]提出了闭环鲁棒的CRT多基线高程反演技术，提高了CRT多基线高程反演技术的噪声鲁棒性，可有效地从噪声较小的多幅干涉图获取目标高程信息。文献[5-7]提出了多基线最大似然函数(maximum likelihood，ML)法，该方法利用真实相位与缠绕相位符合圆高斯分布的性质，使用贝叶斯条件概率对真实相位进行估计，在低噪声情况下能得到较好的解缠结果，但在噪声较大时，解缠结果出现大量“毛刺”点，算法鲁棒性较差。袁志辉等[8]在ML的基础上引入了坏点判断和加权均值滤波，提高了算法精度。Ferraiuolo等[9]则提出了基于高斯马尔可夫随机场(Markov random fields，MRFs)的最大后验概率(maximum a posteriori，MAP)估计方法，利用马尔可夫随机场统计分布模型来描述高程的先验分布，将高程反演转化为能量函数最小化的优化问题，再使用迭代条件模型进行求解。基于马尔可夫随机场的MAP算法，需要估计复杂的超参数，耗时较长。Ferraioli等[10]提出一种全变分(total variation，TV)模型的MAP算法(即TV+MAP算法)，避免了复杂的超参数估计，大大缩短了运行时间。谢先明等[11]提出了一种融合残差点信息的TV+MAP算法，通过残差信息对高程图中的坏点进行适当加权更新获得最终估计高程，提高了TV+MAP算法的精度。针对能量函数最小化的研究，多种基于置信传播[12]、顺序树重加权消息传递[13-14]，以及多标签图割[15-17]的算法相继被提出，并在文献[18]中进行了详细的分析和比较。

与此同时，Yu等[19]提出了基于聚类分析的多基线InSAR高程反演算法，能在信噪比较高的干涉图中获得较好的结果，且该算法效率较高，不利之处在于该算法聚类效果易受噪声影响；Liu等[20]在此基础上提出了一种基于密度聚类的相位解缠算法，提高了聚类算法的抗噪性能。Li等[21]提出了子空间联合处理算法，通过子空间投影将真实相位与噪声分离；随后，索志勇等[22]在此基础上对其信号空间维度估计的准确性和算法复杂度进行改进，有效提高了算法性能。文献[23-24]成功地将深度学习框架应用到InSAR高程重建中，将高程重建转化成相位模糊数的多分类问题，利用卷积神经网络进行高程重建。

在上述算法中，ML、MAP和TV+MAP算法是目前多基线InSAR高程反演算法中最常用的算法。ML算法没有考虑邻域间的约束关系，算法鲁棒性较差；MAP算法虽然引入了邻域约束关系，但需要迭代估计超参数，运行效率低，且不连续区域邻域约束的引入将造成严重的误差传递效应；TV+MAP算法能有效避免超参数估计，但同样未考虑不连续边界邻域约束导致的误差传递问题。为了解决上述问题，本文提出一种基于边缘检测与路径跟踪策略的多基线InSAR高程反演方法。该算法分为2个步骤：第1步先用最大似然估计获取粗略的地形高程，再用Sobel算子对滤波后的粗略地形高程进行边缘检测，获得地形的不连续边界；第2步首先建立优化的多基线InSAR高程反演模型，随后利用单通道InSAR相位解缠技术中的路径跟踪策略引导构建的多基线InSAR高程反演模型，沿高质量像元到低质量像元的路径重新反演目标高程，并在高程反演过程中根据边缘检测结果判断是否引入邻域约束，既有利于提高算法在连续区域的抗噪性，又可避免邻域约束在不连续区域引起的误差传递现象，从而达到增强算法鲁棒性的目标。

1 多基线InSAR高程反演及相关算法

在多基线InSAR高程反演模型中，地形高程、真实相位与缠绕相位之间存在的关系如式(1)、式(2)所示。

φi=φi(x)+2n(x)·π

(1)

(2)

式中：φi代表第i幅干涉图的真实相位；φi代表第i幅干涉图的缠绕相位(-π≤φi<π)；n代表整数倍的缠绕数；x代表对应像元的坐标位置；h为对应的地表高程值；λ为雷达工作波长；R为主天线到目标场景中心的距离；α为水平基线角；Bi为第i条基线的长度；κi为第i条基线对应的高度灵敏度。

1.1 ML算法

ML算法假设真实相位与缠绕相位符合圆高斯分布[25]，则缠绕相位的概率密度函数表达如式(3)所示。

(3)

式中：bi=cos (κih-φi)；γi为第i幅干涉图的相干系数。ML算法利用L幅单视干涉图的联合概率密度似然函数直接重建高程(式(4))。

(4)

ML算法利用了多基线InSAR干涉相位相互独立的特性，有效减少了似然函数最大概率值的周期出现。

1.2 MAP算法

MAP算法是在ML算法的基础上，引入马尔可夫随机场，约束相邻像素点的高程范围，是一种精度较高的多基线高程重建算法。MAP算法模型表达如式(5)所示。

hMAP=argmax lnFML(φ|h)·g(h，σ)

(5)

根据Hammersley-Clifford理论，任何类型的马尔可夫随机场都可以用Gibbs分布表达,如式(6)所示。

(6)

(7)

式中：Nx表示像素点x邻域的像元集合，一般取8连通域；σxy为超参数集合σ的元素，代表高程的局部变化特征，一般可采用期望最大化算法[26](expectation maximization，EM)对其进行估计。结合式(5)，MAP算法经化简后的表达如式(8)所示。

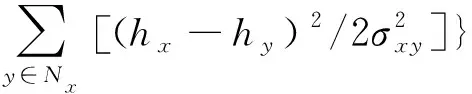
(8)

对于式(8)的求解，本文实验中均使用Pascazio提出的条件迭代模型算法进行10次迭代求解。相对于ML算法，MAP算法重建高程的精度更高。由于式(7)中复杂的局部约束关系，使得MAP算法适用于各类地形，但该方法需要重复迭代估计超参数，算法耗时较长。

1.3 TV+MAP算法

TV模型由于其对不同背景信息强大的适应能力，成为图像处理中最有用的先验模型。在SAR应用中，TV模型主要用来做图像复原。Ferraioli等将TV模型成功应用到InSAR高程重建，提出了TV+MAP算法，其TV能量函数表达如式(9)所示。

(9)

(10)

与高斯马尔可夫随机场模型不同的是，TV模型为非局部模型，选择非局部先验能量避免了对局部超参数矢量的估计，从而简化模型，提升了算法的运算效率。但算法对地形的适应性也因为没有局部先验而降低。

2 本文方法

本文方法分为2个步骤：第1步直接利用多基线最大似然估计算法从多幅不同基线的干涉相位图中获取粗略的地形高程，随后利用窗口为3×3的中值滤波与均值滤波算法对ML算法获取的地形高程进行滤波，接着用Sobel算子对滤波后的地形高程图进行边缘检测，获得地形的不连续边界；第2步首先建立优化的多基线InSAR高程反演模型，随后利用传统单通道InSAR相位解缠技术中的路径跟踪策略引导构建的多基线InSAR高程反演模型沿高质量像元到低质量像元的路径反演目标高程，并在高程反演过程中根据边缘检测结果判断是否引入邻域约束，既有利于提高算法在连续区域的抗噪性，又可避免邻域约束在不连续区域引起的误差传递现象，从而达到增强算法鲁棒性的目标。

2.1 基于Sobel算子的边缘检测

邻域约束是MAP以及TV+MAP算法的核心，有利于在干涉图连续区域得到高精度的相位解缠结果。然而，在不连续区域邻域约束的引入将造成严重的误差传递效应，导致MAP和TV+MAP算法鲁棒性降低。如何准确地在连续区域引入邻域约束且在不连续区域阻断邻域约束是提升相位解缠算法精度的关键。为解决这个问题，本文先用ML算法获取粗略的地形高程图，随后利用窗口为3×3的中值滤波算法与均值滤波算法对ML算法获取的地形高程图进行滤波，接着再用Sobel算子对滤波后的地形高程图进行边缘检测，能够有效地检测出地形的不连续边界并得到标记边界像元的二值图像，记为edge。

关于边缘检测中的阈值设置问题，以图1(a)中的美国Long’s Peak公园真实地形高程数据为例，在传统单基线InSAR高程重建算法中，当干涉图相邻像元之间高程超过其基线所对应高度模糊数的二分之一时，则无法满足相位连续性假设。以长基线干涉图对应的高度模糊数的二分之一作为边缘检测阈值，可以检测出更多边缘细节，但这些细节边缘并不是真正意义上的不连续边界，如图1(a)和图1(b)白色矩形框所示。使用短基线所对应高度模糊数的二分之一作为边缘检测阈值，可以更有效检测出真正的不连续边界，如图1(c)所示。

图1 边缘检测示意图

2.2 优化的高程反演模型

优化的高程反演模型如式(11)、式(12)所示。

图2以不连续像元可能出现的一种分布情况进行一般性分析，通过在不连续边界周围自适应地调整邻域约束强弱，能够有效避免误差传播并提高算法的鲁棒性。

图2 中心像元邻域不连续边界示意图

算法流程及步骤如下所示。

算法开始步骤 1 (边缘提取)步骤1.1:利用多基线ML算法从多幅不同基线的干涉相位图中获取粗略的地形高程。步骤1.2:利用窗口为3×3的中值滤波与均值滤波算法对多基线ML算法获取的地形高程图进行滤波。步骤1.3:利用Sobel算子对滤波后的地形高程图进行边缘检测,得到标记了不连续边界点的二值图像edge。步骤2 (高程重建)步骤2.1:在多基线InSAR干涉图相位质量图中选择5～10个质量较好的像元,利用ML算法获取其高程估计值。步骤2.2:在已反演高程的像元中,将它们4邻域中未解缠的像元按相位质量从大到小排列,作为邻接列表。步骤2.3:取出邻接列表中质量最好的一个像元x,根据边缘检测得到的二值图像进行判断。若该像元为不连续边界像元,则利用式(11)获取高程估计值;若该像元为连续像元,则计算该像元8邻域中非边界已解缠像元的高程平均值hyunwrap,并利用式(12)获取高程估计值,将像元x的4邻域中未高程反演的像元嵌入邻接列表。步骤2.4:判断邻接列表是否为空,非空则执行步骤2.3;为空,则算法结束,得到估计高程。算法结束

在步骤2.1中，选取5～10个点利用多基线ML算法获取其高程估计值作为初始参照点。理论上只需要选取一个质量最好的点获得其高程估计值作为初始参照点即可，但为了增加邻接列中像素点数量，提高算法的稳健性，建议选取5～10个点。

3 实验验证及分析

为验证算法的有效性，且更好地突出边缘检测和优化TV高程模型结合路径跟踪策略在本文方法中的作用，本文针对封闭式线状突变地形、连续地形以及开放型线状突变地形数据进行实验，并在仿真实验中将本文方法与多基线InSAR高程重建技术中经典的ML、MAP以及TV+MAP算法进行对比，检验本文方法性能。本文采用归一化均方根误差计算实验结果误差，计算方法如式(13)所示。

(13)

式中：hunwrap为估计高程；h为真实高程值；M和N分别为方位向和距离向的像元个数；p和q为像元二维坐标。

3.1 仿真实验1

在实验1中采用如图3(a)所示大小150像素×150像素的模拟城市地形。该模拟城市地形图中存在多处突变边缘，且相邻点之间的最大高程差为150 m。InSAR系统参数为表1所示，3条基线分别为202.5 m、179.4 m、143.6 m。

图3(c)是信噪比为7.4 dB的长基线干涉图。图3(d)、图3(e)分别为ML估计高程图、经过中值滤波和均值滤波的ML估计高程图。图3(f)为Sobel算子对图3(d)进行边缘检测后得到的标记了不连续边界的二值图像。图3(g)至图3(i)分别为MAP 10次迭代估计的结果、TV+MAP估计结果和本文方法估计结果。图3(j)至图3(l)分别为MAP、TV+MAP和本文方法对应的估计高程误差。从图3(d)至图3(f)可以看出，ML估计高程虽然存在大量的毛刺点，但其地形的边缘特性依然清晰可见，经过中值和均值滤波处理后，能得到保持良好边缘特性的高程图，使用Sobel算子进行边缘检测能够有效提取出地形的不连续边界点。表2给出了各算法的高程重建的误差，以及针对突变区域的高程重建误差。结合表2以及图3(g)至图3(l)可以看出，本文方法针对该地形的高程重建效果与TV+MAP算法效果相当，都能够较好地估计出地形高程，且误差主要集中在不连续的边界处。由于该地形高程值较为单一，因此本文方法相较于TV+MAP算法精度提高并不明显。

图3 模拟城市地形高程反演实验结果对比

表1 多基线InSAR系统基本参数

表2 算法性能对比

3.2 仿真实验2

为了进一步验证本文方法在连续区域的处理效果，在实验2中，采用如图4(a)所示大小为256像素×256像素的连续地形Peaks进行实验。图4(b)为Peaks地形的二维高程图，图4(c)是含噪声的长基线干涉图，模拟InSAR系统参数与实验1相同，3条基线分别为415.5 m、272.2 m、151.8 m。

图4(d)、图4(e)分别为ML估计高程图、经过中值滤波和均值滤波的ML估计高程图。图4(f)为Sobel算子对图4(e)进行边缘检测后得到的不连续边界标记图。从图中可以看出，ML估计高程布满了密集的毛刺点，经过滤波处理后仍然存在部分毛刺点，由于地形本身是连续的，这些滤波处理后的毛刺点在边缘检测中被成功过滤。从图4(g)至图4(i)和表3的结果可以看出，在连续区域中，本文方法中优化的TV高程反演模型在路径跟踪策略的引导下进行递推估计,对算法的高程重建精度有很大提升。

图4 Peaks地形高程反演实验结果对比

表3 算法性能对比

3.3 仿真实验3

为了进一步综合性地验证本文算法在连续区域及不连续区域的性能，在实验3中，采用如图5(a)所示，大小为458像素×152像素的美国国家公园Long’s Peak地形的真实数字高程，该地形右侧有一条垂直断裂带将地形分割成2块连续的区域，高程范围为0～127 m，最大高程差为127 m。图5(c)是长基线干涉图，模拟InSAR系统参数与实验1相同，3条基线分别为415.5 m、272.2 m、151.8 m。

图5(d)、图5(e)分别为ML估计高程图、经过中值滤波和均值滤波的ML估计高程图。图5(e)为Sobel算子对图5(d)进行边缘检测后得到的不连续边界标记图。图5(g)至图5(i)分别为MAP 10次迭代估计的结果、TV+MAP估计结果和本文方法估计结果，从图中可以看出，本文方法高程重建效果最好。图5(j)至图5(m)分别为ML估计、MAP 10次迭代估计、TV+MAP估计以及本文方法估计高程与真实高程对比的误差图，结合表4可以看出，本文方法有效提取出了地形不连续边界，通过阻断不连续边界处的邻域约束，避免误差传递，在连续区域引入邻域约束的同时，结合路径跟踪策略进行递推估计，有效地提高了算法的鲁棒性，且算法的运行效率也与TV+MAP模型相当。

图5 Long’s Peak地形高程反演实验结果对比

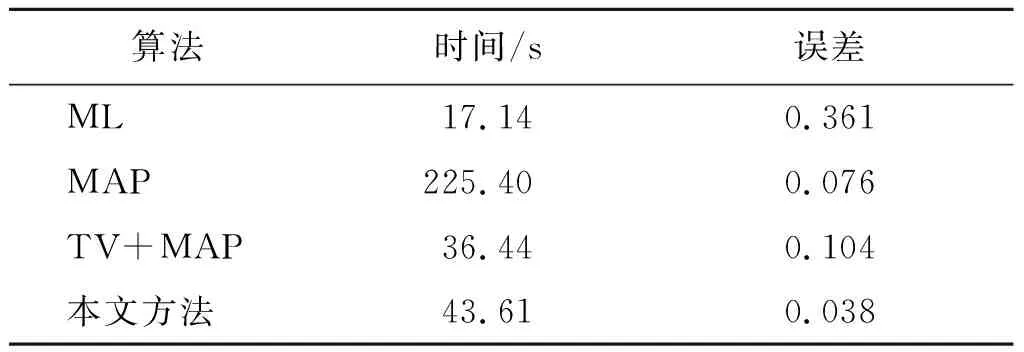
表4 算法性能对比

4 结束语

论文提出了一种基于边缘检测与路径跟踪策略的多基线InSAR高程反演算法。通过提取地形的不连续边界，在连续区域引入邻域约束并结合路径跟踪策略进行高程重建，有效地提高了算法在连续区域的鲁棒性；在不连续边界处阻断邻域约束，避免了误差传递现象。通过3组仿真实验证明本文方法对于不同的地形进行高程重建时都具有较高的精度、效率和稳健性。