具有Allee 效应的捕食-食饵扩散模型定性分析

李海侠

(宝鸡文理学院数学与信息科学学院，宝鸡 721013)

1 引言

1931 年Allee 在研究过程中发现群居的生活状态有利于种群的增长，但是密度太大又会抑制种群的生长甚至会因为资源争夺而走向灭绝.对于每一个种群来说，必定存在着它独立的最适合自身生长繁殖的最佳密度，这就是Allee 效应.已有大量的理论和实验证明，Allee 效应与种群的灭绝密切相关，在很大程度上能增加低密度种群的灭绝风险，尤其对小种群、分散种群、稀有种群以及濒临灭绝种群的动力学行为具有非常大的影响.因此，研究具有Allee 效应的生物模型对生物保护具有很重要的意义，近年来受到了生物学家和数学家的很大关注[1-10].

本文在齐次Dirichlet 边界条件下考虑如下具有B-D 反应函数和Allee 效应捕食-食饵扩散模型

为了得到重要的结论，这节最后我们给出一些预备知识.

-Δψ+q(x)ψ =λψ, x ∈Ω, ψ =0, x ∈∂Ω,

则λ1(q)连续依赖q，λ1(q)是简单的.而且，如果q1≤q2, q1/≡q2，则λ1(q1)＜λ1(q2).为了简单起见，定义λ1(0)为λ1，相应于λ1的主特征函数记为ψ1.

非线性问题

众所周知，若a ＞λ1，则(2)存在唯一正解.我们定义唯一正解为θ(a,r).特别地，记θ(a,1)为θa，则θa＜a 且θa连续依赖a.

2 正解的存在性、不存在性和唯一性

考虑单物种问题

根据文献[6]可得如下引理.

引理1[6]系统(1)的任意正解(u,v)有先验估计

引理2[6]如果系统(1)有正解，则a1＞λ1, a2＞λ1.

为了计算不动点指数，引入以下记号

取q 充分大，使得q ＞max{m/k1+p1/d,a2(a1+k2)/k2}.定义算子A:E →E 为

证明 根据已知条件和定理1 可知系统(1)存在正解.采用反证法证明唯一性.假设系统(1)存在两个不同的正解(u1,v1)和(u2,v2)，其中ui＞0, vi＞0(i = 1,2).由比较原理和引理1 可知u*≤ui≤u*, v*≤vi≤v*，这里u*, v*分别为如下问题的唯一正解

令Φ=u1-u2, Ψ=v1-v2，则

因为(u1,v1)是系统(1)的正解，所以根据特征值的变分原理可知

于是，公式(4)表明

同理，由(5)式有

令

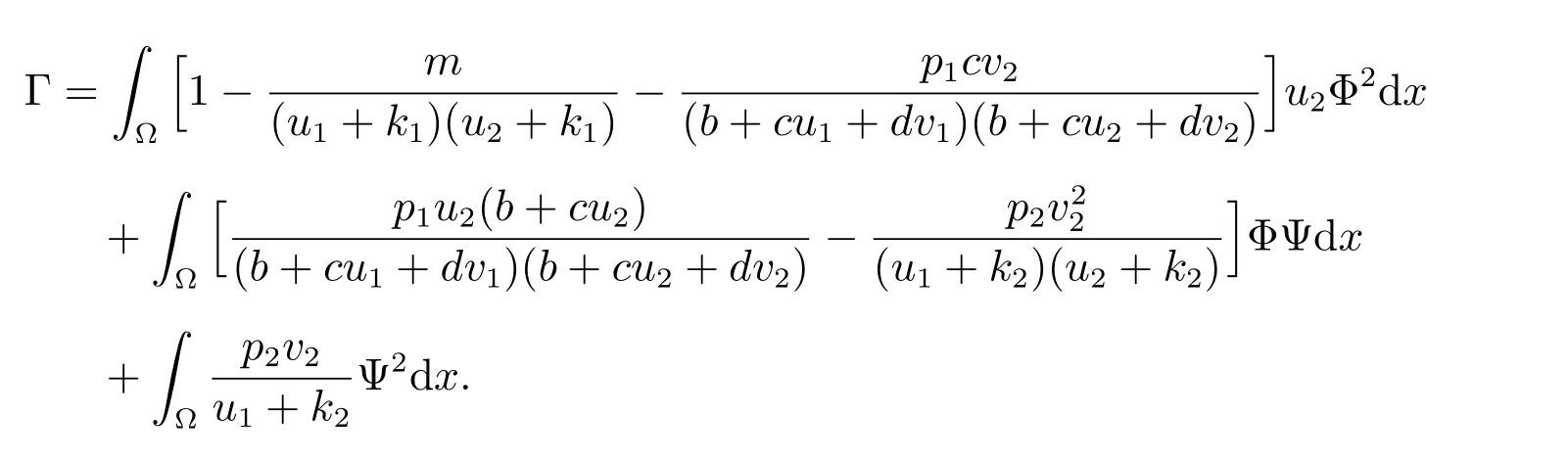
最后，令

经过计算并结合已知条件可得

故Γ ＞0.而式(6)和(7)可知Γ ≤0，矛盾.因此结论成立.

3 正解的确切重数和稳定性

本小节应用扰动理论和不动点指数理论讨论参数c →∞时，系统(1)正解的确切重数和稳定性.易看出当c →∞时，系统(1)的正解有两种类型，即如果(u,v)是系统(1)的任意正解，则对于充分大的c，(u,v)趋于如下问题的正解

或者(cu,v)趋于如下问题的正解

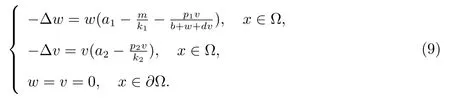
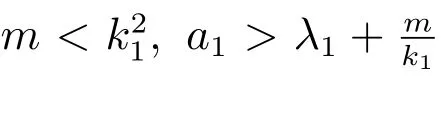
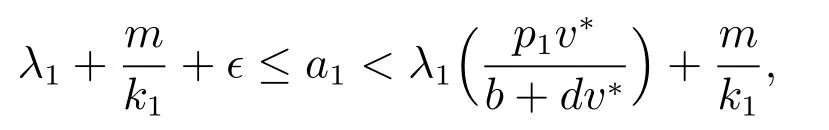
则系统(1)至少存在两个正解.

如果a2＞λ1，则问题(9)等价于如下问题

对于问题(10)，用类似文献[11]的证明方法有如下引理.

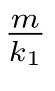
时，(10)的正解(若存在)唯一且非退化.

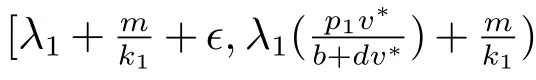
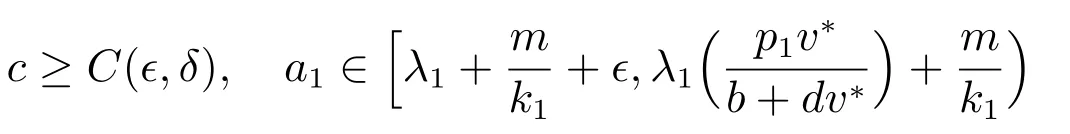
且(u,v)是(1)的正解，则：

这里w 是(10)的正解，v**为如下问题的正解

而且，若(a)情形出现，则正解(u,v)非退化且线性稳定.

证明 采用反证法证明.假设存在

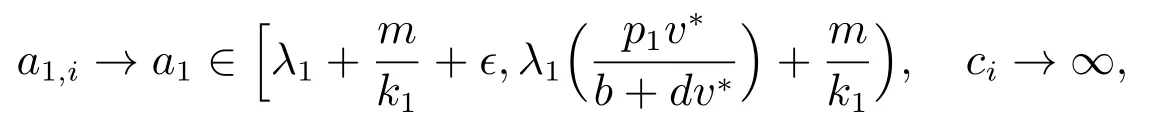
(i) 若ci‖ui‖∞→∞，则当i →∞时，ui→u*.因此vi→0 或vi→v**.而a2＞λ1，所以必有vi→v**，即(ui,vi)→(u*,v**).这与假设(ui,vi)远离(u*,v**)矛盾；

(ii) 若ci‖ui‖∞一致有界，则当i →∞时，ui→0.于是vi→v*.设ciui= wi，则wi满足

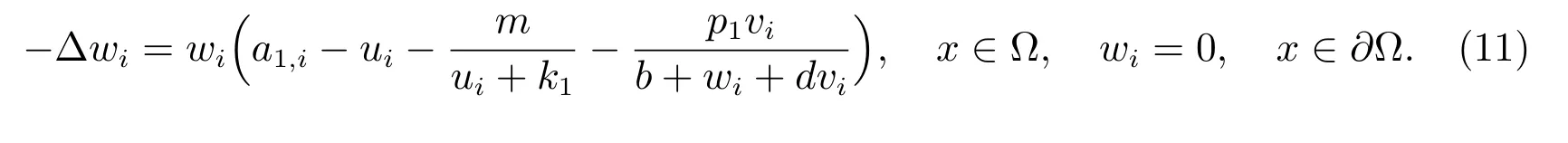
则系统(1)恰好有两个正解，一个渐近稳定而另一个不稳定，这里ϵ0在引理5 中给出.

证明 根据引理7 分两步证明.首先证明当c 充分大时，(1)接近(u*,v**)的正解唯一且渐近稳定.引理7 可知系统(1)接近(u*,v**)的任意正解非退化且渐近稳定.故只需证明接近(u*,v**)的正解(u,v)唯一.取δ′＞δ 充分小，这里δ 在引理7 中给出.设

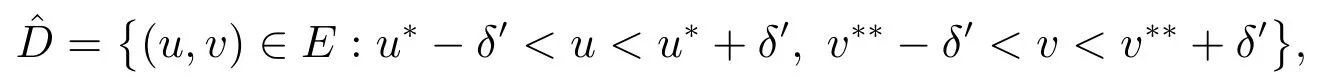
由此证明了系统(1)接近(u*,v**)的正解(u,v)唯一.

接下来证明(1)存在唯一且不稳定的类型(b)的正解.首先证明唯一性.

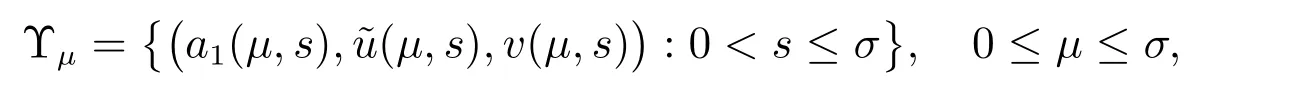
其中

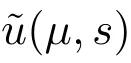
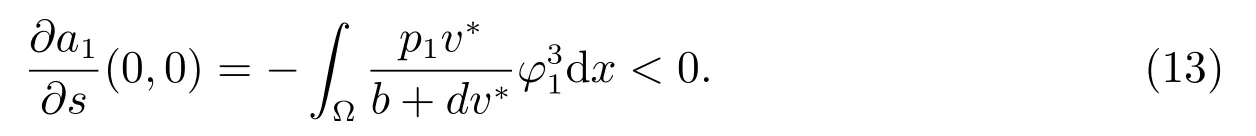
因为a1(μ,s)连续，所以存在σ1∈(0,σ]，使得

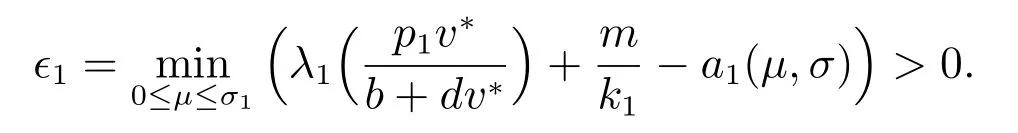
于是若

则对于任意μ ∈[0,σ1], a1(μ,σ) ≤a1.这样我们得到对于任意的μ ∈[0,σ1], Υμ一致覆盖a1-区域

则(1)恰好有唯一(b)类型的正解.

最后，我们证明(b)类型的正解不稳定.令L1是(1)在(u,v)处带有特征值η1和特征函数(ξ1,ζ1)的线性化算子.令L2是(12)在(cu,v)处带有特征值η2和特征函数(ξ2,ζ2)的线性化算子.易证ξ1=ξ2, ζ1=cζ2, η1=η2.于是证明(12)于(cu,v)处的线性化算子在分歧曲线Υμ的任意点处有负的特征值γ 即可.通过文献[14]可得存在ν ＞0 和C1函数

则

基于上面引理，这节最后给出c 充分大时确定(1)正解确切个数的重要结果.

则系统(1)恰好有两个正解，一个渐近稳定另一个不稳定.其中

证明 令

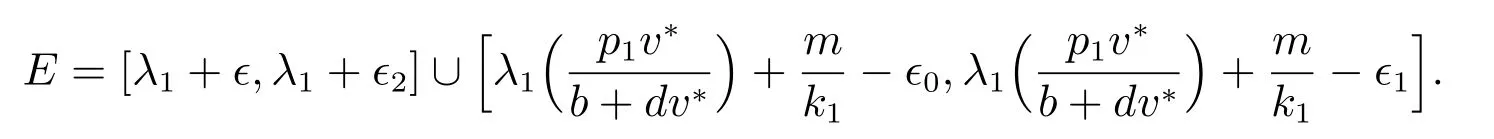
引理8 可知只需证明当a1∈E 时，(1)恰好有一个渐近稳定的正解和另一个不稳定的正解即可.引理7 表明如果c 充分大且

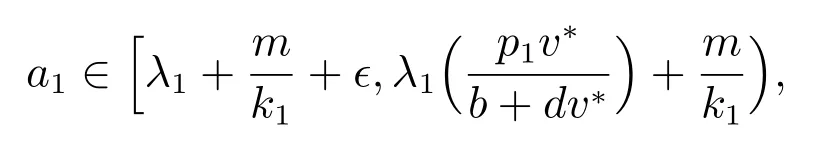
则(1)存在两类形式的正解.采用类似引理8 的证明过程易证得，若a1∈E，则(1)存在唯一接近(u*,v**)类型(a)的渐近稳定的正解.

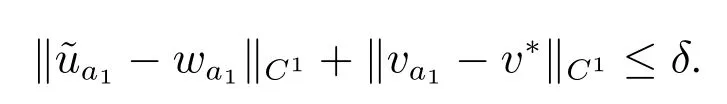
接下来，证明(1)具有类型(b)的正解不稳定.定义算子B 和B0分别如下

考虑如下特征值问题

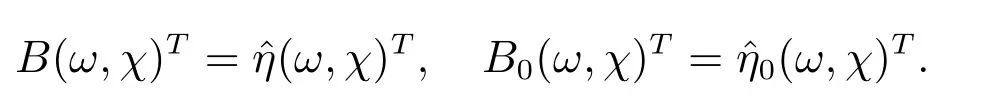
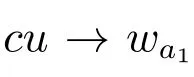
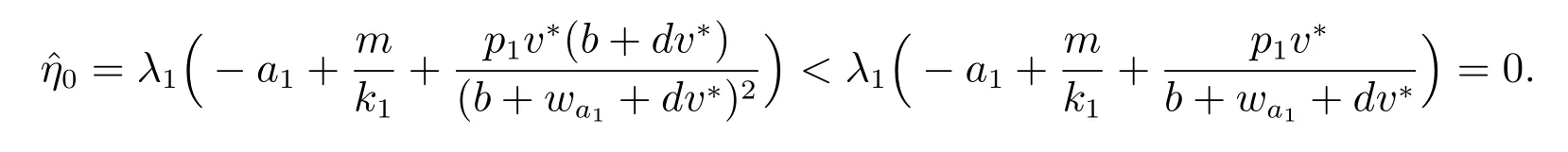
4 讨论与结论

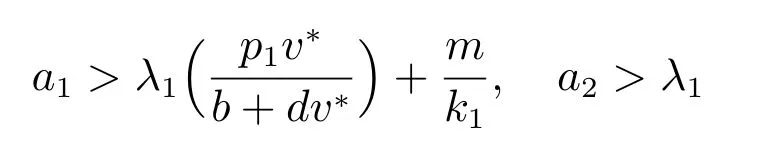
且捕食者对食饵的处理时间c 的影响充分大时食饵和捕食者不但能够共存，而且系统恰好存在两个正解.从生物意义上来讲，研究结果表明当参数满足一定条件时系统出现了生物上所谓的多态性，而且食饵和捕食者将会以稳定均衡的形式共存.这说明保持适合种群自身生长繁殖的最佳密度、控制种群适当的增长率以及合理地开发和利用生物资源对生物种群保护和维持生态平衡具有非常重要的意义.Allee 效应增加了系统动力学行为的复杂性，本文得到的主要结论既补充和完善了以往相关文献的结果，又丰富了齐次Dirichlet 边界条件下具有Allee 效应的生物扩散模型的研究内容.