m 相依序列的样本分位数核估计的中偏差和大偏差
2021-03-30谢超,陈夏,闫莉
谢 超, 陈 夏, 闫 莉
(陕西师范大学数学与信息科学学院,西安 710119)
1 引言
分位数是统计学中的一个基本概念,它可以用来表示随机变量的某些性质,并且没有任何矩条件的要求.分位数也可以估计呈偏态分布的定量资料的正常值范围,描述呈偏态分布定量数据的离散程度的大小.因此,分位数在统计、金融投资、生物医学等领域都有广泛的应用[1-3].假定总体X 的分布函数为F(·),则总体p 分位数定义为
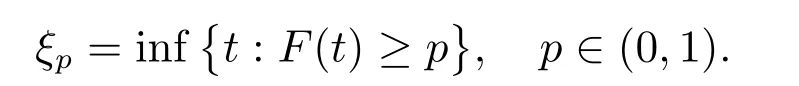
当总体分布未知时,通常用经验分布代替总体分布.假设{Xi,1 ≤i ≤n}为来自总体X 的一组样本,则样本p 分位数定义为

其中

在总体分位数未知时,通常用样本分位数估计总体分位数,众多研究者对样本分位数估计的大样本性质进行了详细讨论.例如,Bahadur[4]在样本独立同分布的条件下,研究了样本分位数的渐近正态性和重对数律.Wu[5]和Sun[6]分别在线性、非线性过程和强混合随机序列下,得到了样本分位数的Bahadur 表示.Xing 和Yang[7]、Ling[8]和Xu 等[9]基于NA 序列,研究了样本分位数的Bahadur 表示.Xu 和Miao[10]在总体分布连续和样本独立同分布的情形下,研究了样本分位数的大偏差和中偏差原理.
样本分位数形式简单、方便易求,但构造样本分位数所使用的经验分布函数没有考虑总体分布的光滑性.因此,Nadaraya[11]提出了样本分位数核估计方法,该方法利用核函数来构造光滑分位数估计.基于核函数K(·),总体分布F 的光滑核估计定义为
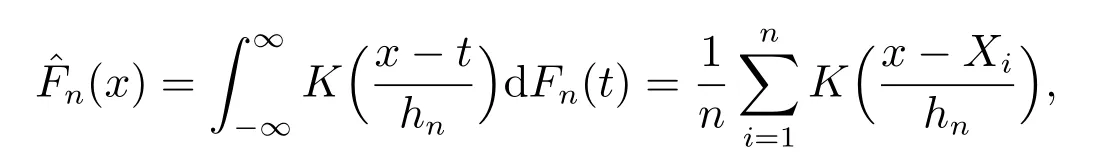
其中{hn}为正数序列,且hn→0(n →∞).因此,ξp的光滑样本分位数核估计定义为
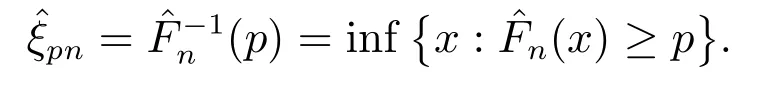
近年来,众多研究者讨论了样本分位数核估计及其渐近性质.例如,Falk[12]基于均方误差,研究了样本分位数核估计和样本分位数估计的渐近相对效率问题.Yang[13]得到了样本分位数核估计与样本分位数估计具有相同的渐近分布,并且给出其均方收敛速度.Sun 和Zheng[14]在左截断和右删失数据下,研究了样本分位数核估计的Bahadur 表示.Cai 和Roussas[15]在样本正、负相协情形下,研究了样本分位数核估计的逐点相合性、渐近正态性和弱收敛性.He 等[16]研究了独立同分布情形下,样本分位数核估计的中偏差和大偏差原理.
由于相依随机序列削弱了独立性的限制,因此得到了众多学者的关注和研究,尤其是关于m 相依序列的研究.例如,陆传荣[17]和苏淳[18]分别研究了m 相依序列的弱收敛和渐近正态性.唐晓静和秦侠[19]讨论了m 相依序列的强大数定律.文献[20-24]研究了m 相依序列的中偏差原理. 候萱等[25]讨论了在m 相依序列样本下,样本分位数的中偏差和大偏差原理.基于上述研究,本文讨论m 相依情形下,样本分位数核估计的中偏差及大偏差问题,将独立同分布样本的结果进行了推广.
首先给出本文所用的预备知识.
定义1 设{Xn;n ≥1}为随机序列,如果存在一非负整数m,使得对每一个k ≥1,集合{X1,X2,··· ,Xk}和{Xk+m+1,Xk+m+2,···}是独立的,则称随机序列{Xn;n ≥1}是m 相依的.
定义2 对于给定的随机序列{Xi;i ∈N},对任意的k ∈N,记

其中Fa,b=σ(Xi;a ≤i ≤b).
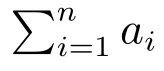

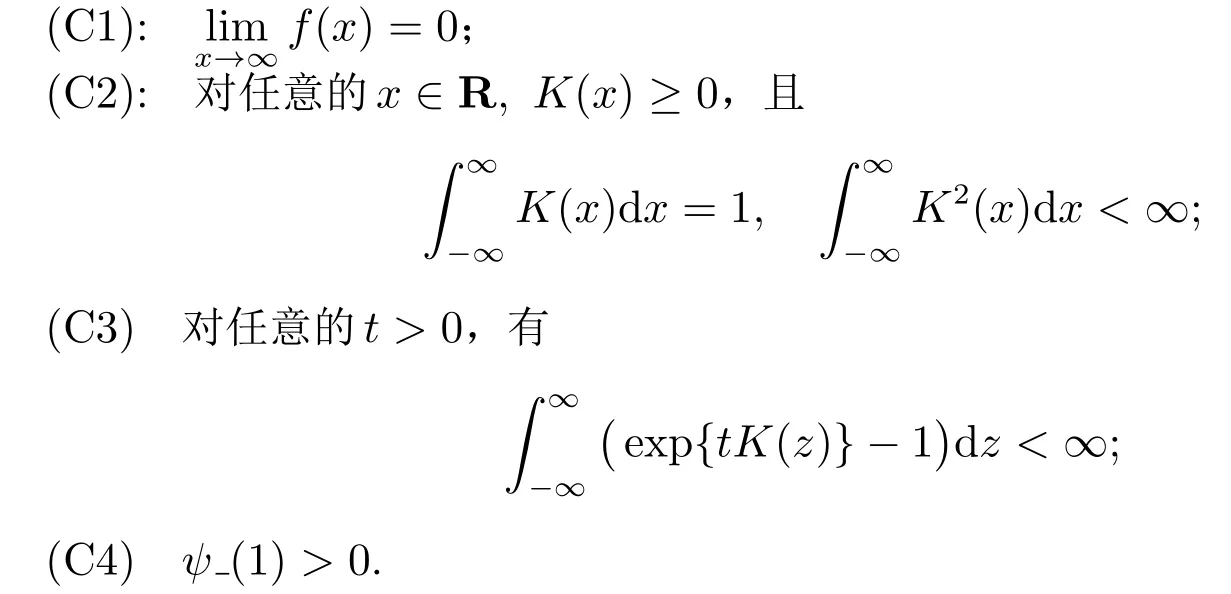
注1 本文定理1 所需条件(C1)-(C3),与文献[16]中研究独立同分布情形的条件(A1)-(A3)相同.条件(C4)是研究m 相依序列的常见假设,见文献[22].但本文定理2 所需条件较文献[16]少了(A4)和(A5),多了条件(C4).这是因为本文利用文献[22]的方法得到定理2 的证明,这不同于文献[16]的证明方法.
2 主要结论及证明
首先,我们给出样本分位数核估计的中偏差原理.
定理1 在条件(C1)-(C3)下,对任意的r >0,有

证明 易知

由文献[16]的定理1 知

同理,有

其中
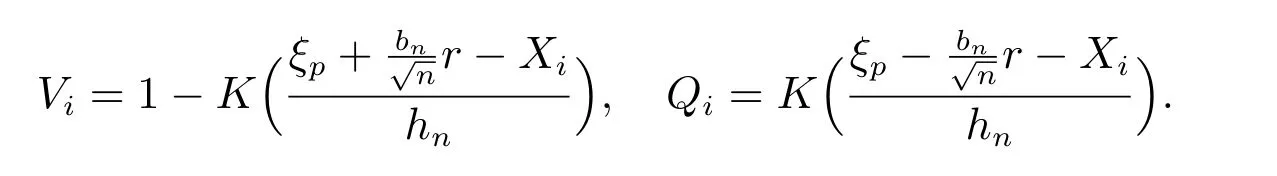
由G¨artner-Ellis 定理知[26],要证定理1 成立,只需证明

下面先证

由Vi的定义知,{Vi-EVi,i ≥1}是m 相依的零均值平稳序列.为了得到中偏差结果,计算其Cramer 函数
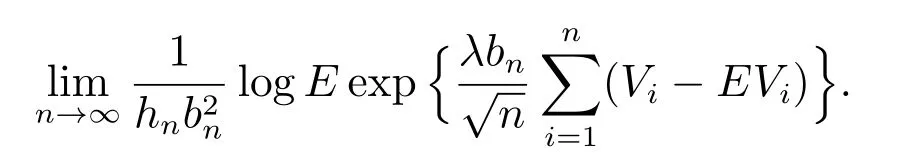

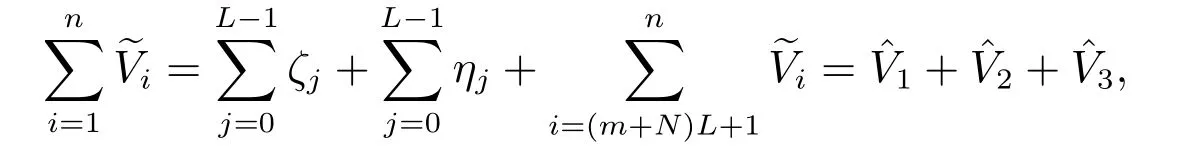
对任意的p1>1, p2>1,取相应的q1, q2,使得
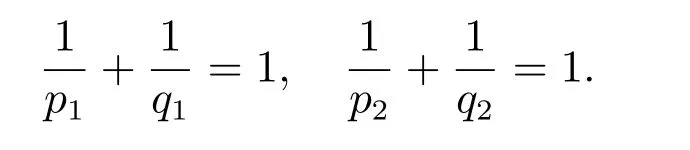
由引理1 得
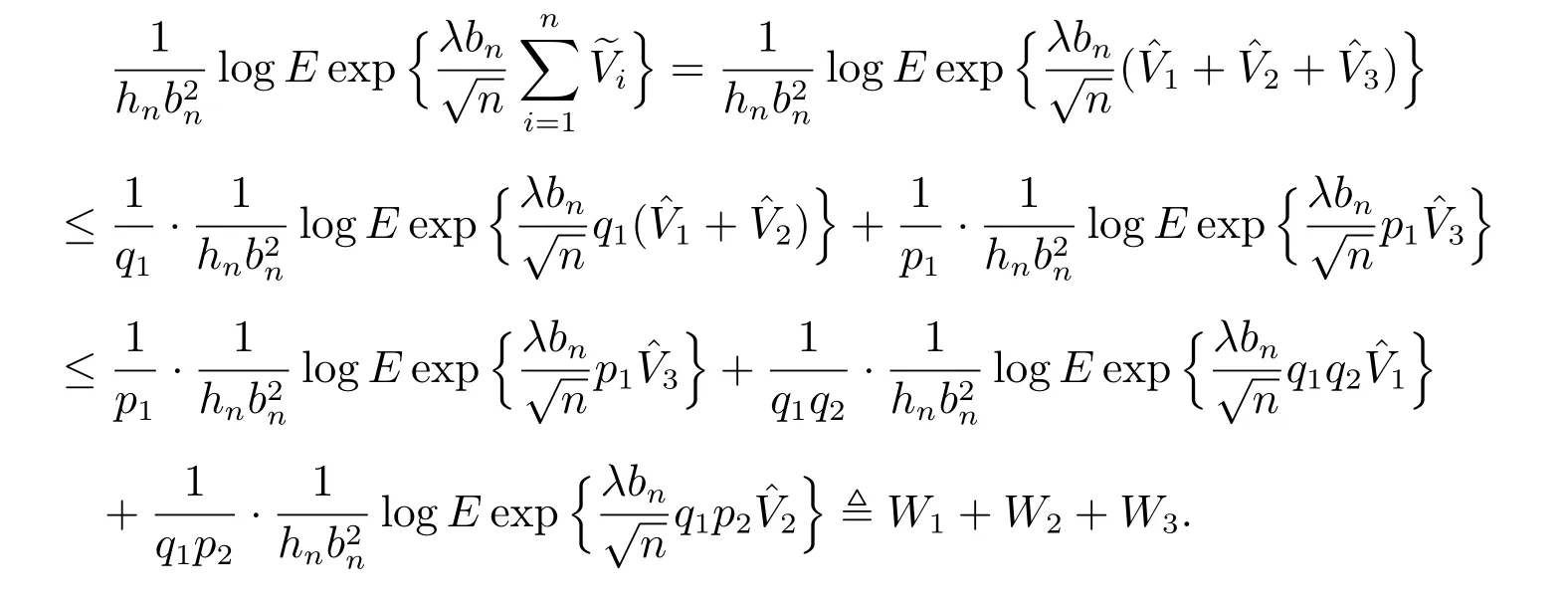
对W1,有
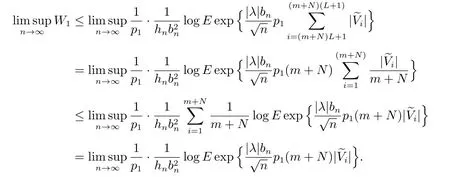
取
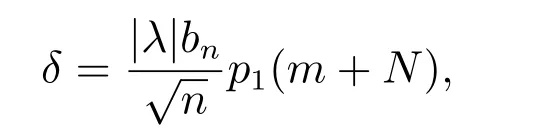
则δ →0.由文献[16,21],易知
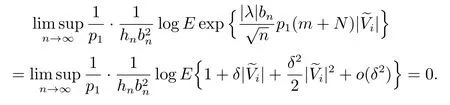
因此

对W2,有
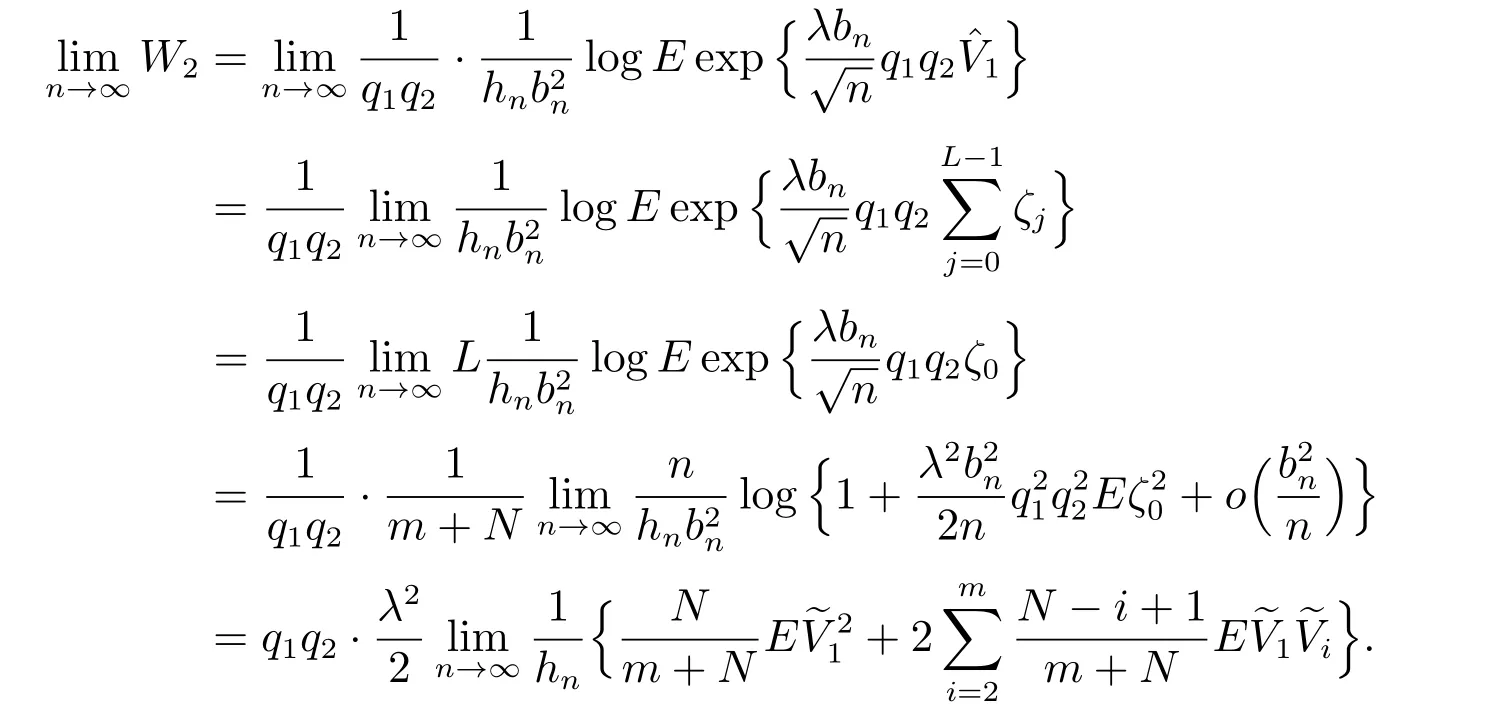
由文献[16]定理1 和文献[27]的引理2.2,可得
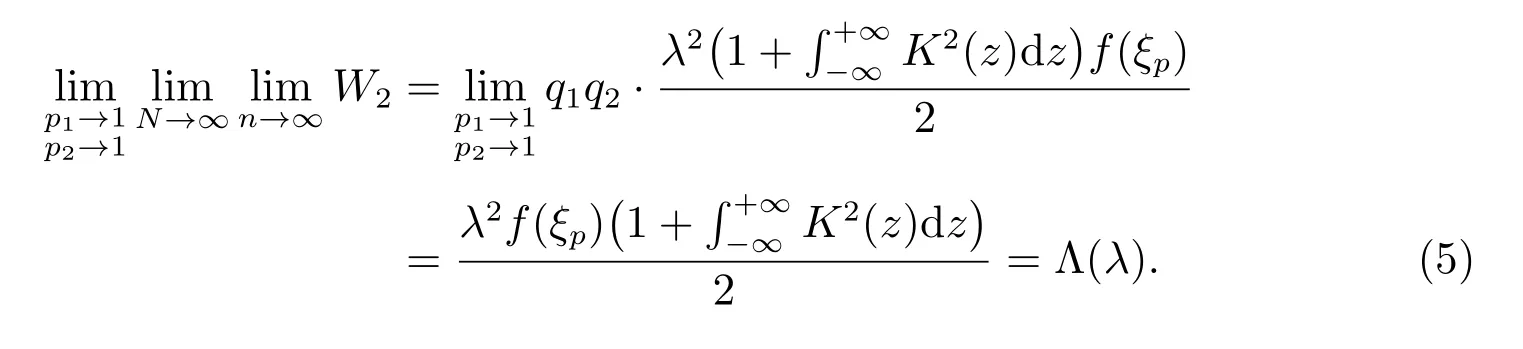
对W3,有
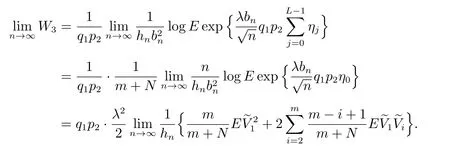
令N →∞,有

结合式(4)-(6),易知
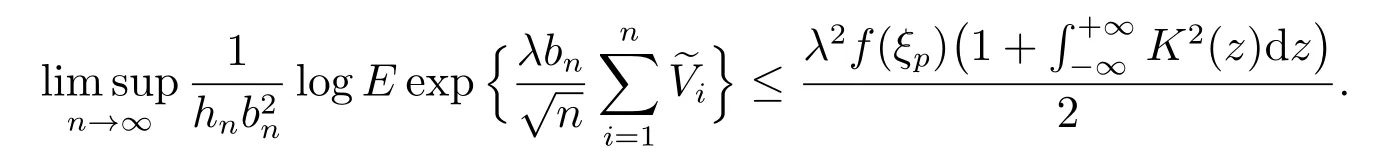
下面只需证明
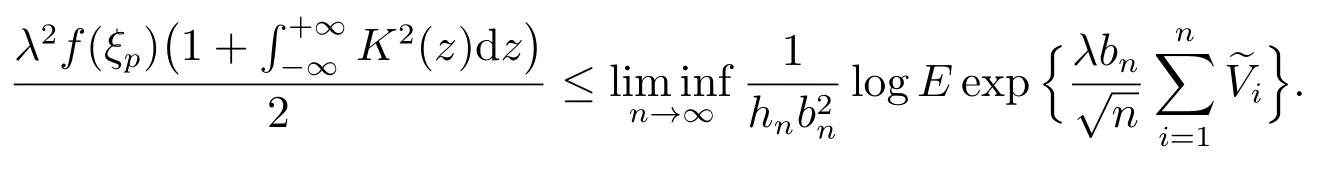
由于
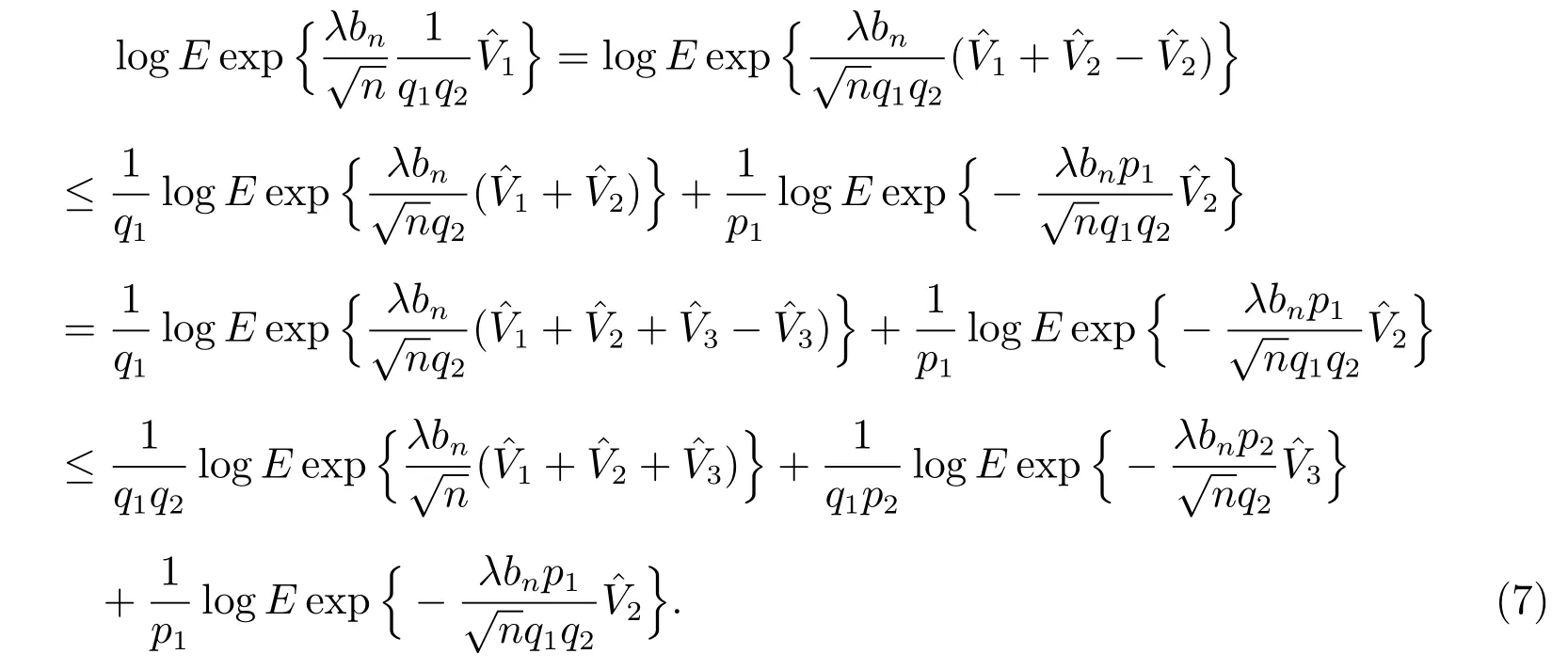
与式(4)-(6)类似,有

结合式(7)-(10),可知
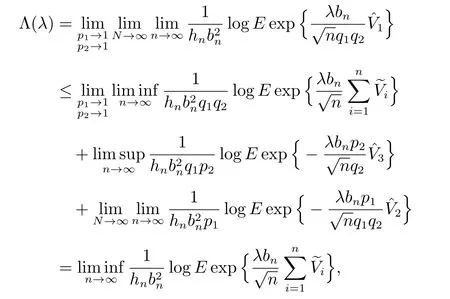
从而
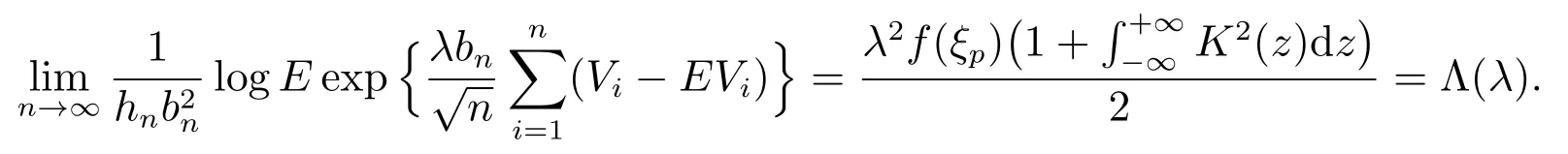
同理,可得
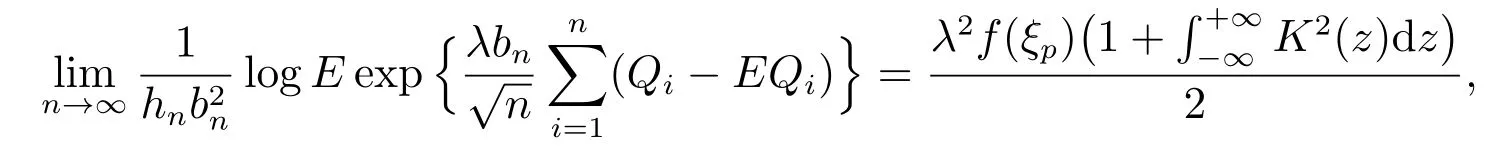
因此,定理1 证明完毕.
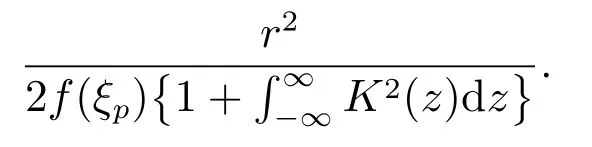
其次,下述结果给出了样本分位数核估计的大偏差原理.
定理2 在条件(C1)-(C4)下,对任意的开集G ⊂R,有

对任意的闭集F ⊂R,有

其中
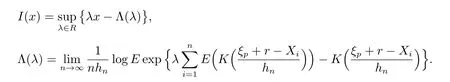
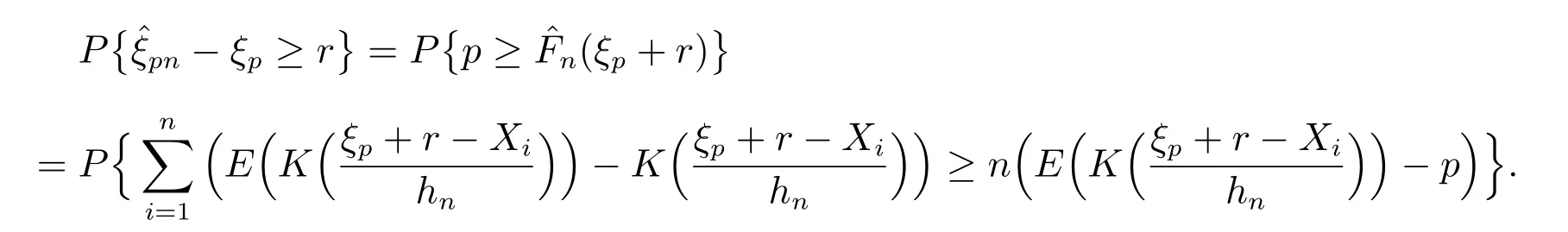
下面证明

满足Cramer 条件.由文献[16]知,对任意的t >0,有
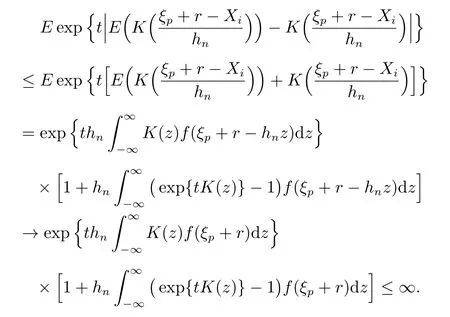
根据文献[22]中的定理3.1,知定理2 成立.
