一类改进的GOM(1,1)模型及其应用

张 锴, 王成勇, 贺丽娟,†

(1- 文华学院数学科学系，武汉 430074; 2- 湖北文理学院数学与统计学院，襄阳 441053)

1 引言

灰色预测模型[1]因建模过程简单，并且在能够在样本数据量较小的情况下，得到较为准确的拟合与预测结果，已被广泛应用于交通管理、城市环境、生态农业、能源分析等众多领域[2-4].与传统灰色预测模型不同，GOM(1,1)模型(Grey Opposite-direction Model)[5,6]是基于反向累加生成方法所建立的灰色预测模型，对于具有递减性质的数据序列具有较好的拟合与预测效果.近年来，许多学者从不同角度对GOM(1,1)模型进行了改进，杨知等[7]分析了反向累加生成，改进了模型背景值的计算，给出了GOM(1,1)模型参数求解的优化方法.陈鹏宇[8]根据背景值的几何意义，建立了两种加权背景值的构造形式.练郑伟等[9]在反向累加条件下，对原始序列和生成序列的齐次和非齐次指数特性进行了研究，在此基础上建立了新的GOM(1,1)模型.文献[10-12]将改进的GOM 模型用于沉降预测，文献[13]将优化的GOM 模型用于道路交通事故预测，都取得了不错的效果.

值得注意的是，上述众多文献中，均用常数b 表示灰作用量，将来自外部的扰动视作不变，这样处理可以简化模型计算，却不能较好反映数据发展变化的客观规律.实际上，随着时间和空间的变化，灰色作用量也会随之变化[14-16].本文重视建模过程中灰作用量的动态变化过程，从白化微分方程入手，在一次累加生成序列满足非齐次指数律的条件下，通过积分给出了GOM(1,1)模型的优化背景值，以原始序列和模拟序列的平均相对误差平方和最小为原则，确定时间响应函数中的最优参数，最终形成完整的优化GOM(1,1)模型.

2 反向累加生成及GOM(1,1)灰色预测模型

定义1[5,6]设x(0)=(x(0)(1),x(0)(2),··· ,x(0)(n))为原始序列，令

称x(1)=(x(1)(1),x(1)(2),··· ,x(1)(n))为x(0)的一次反向累加生成序列.

定义2[5,6]设x(0)=(x(0)(1),x(0)(2),··· ,x(0)(n))为原始序列，取

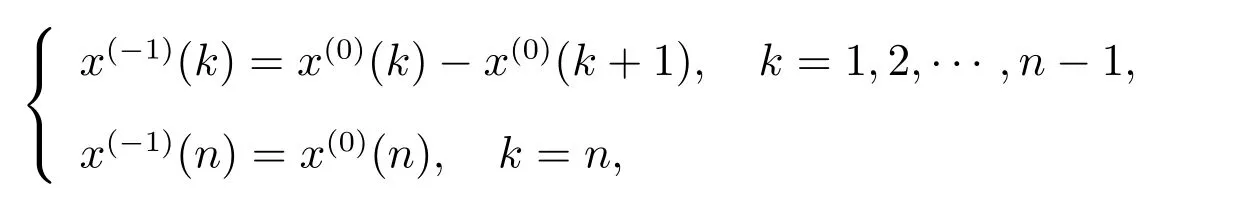
称x(-1)=(x(-1)(1),x(-1)(2),··· ,x(-1)(n))为x(0)的一次反向累减生成序列.

易知

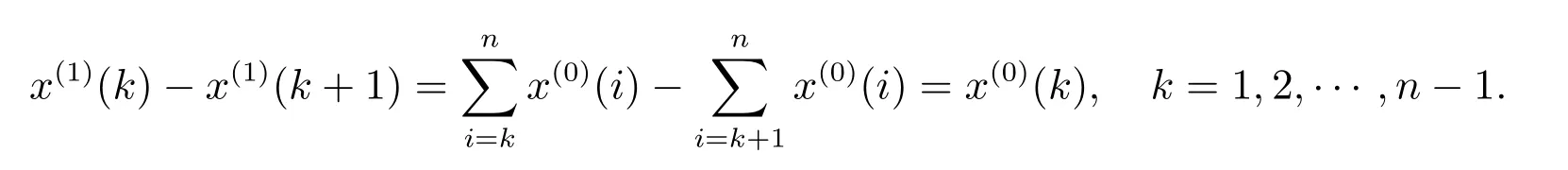
定义3[9]设x(0)为非负准光滑原始序列，x(1)为其一次反向累加生成序列，对x(1)建立基于反向累加生成的GOM(1,1)模型

-x(0)(k-1)+az(1)(k)=b, k =2,3,··· ,n,

其中a 为发展系数，b 为控制系数，z(1)(k)为背景值.

GOM(1,1)模型的白化方程为

定义3 中的模型用常数b 表示灰作用量，并未考虑灰作用量随时间和空间的变化而发展变化的过程；如果将灰作用量近似看作为时间的线性函数，即使用b1+b2k 代替原来的灰作用量，可以对GOM(1,1)模型进行优化.

3 GOM(1,1)灰色预测模型的优化

3.1 灰作用量优化的GOM(1,1)灰色预测模型

定义4 设x(0)为非负的原始序列，x(1)为其一次反向累加生成序列，称

为灰作用量优化的GOM(1,1)模型.

定义5 称

为灰作用量优化的GOM(1,1)模型的白化方程.

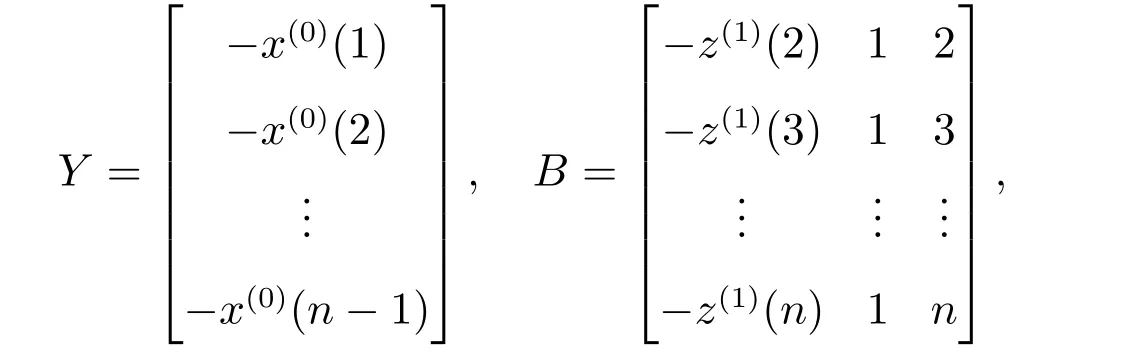
则GOM(1,1)模型(1)的参数估计式为

证明 将数据代入灰色微分方程-x(0)(k-1)+az(1)(k)=b1+b2k，移项得到

-x(0)(1)=-az(1)(2)+b1+2b2,

-x(0)(2)=-az(1)(3)+b1+3b2,

··· ,

-x(0)(n-1)=-az(1)(n)+b1+nb2,

使s 最小的a, b1, b2应满足

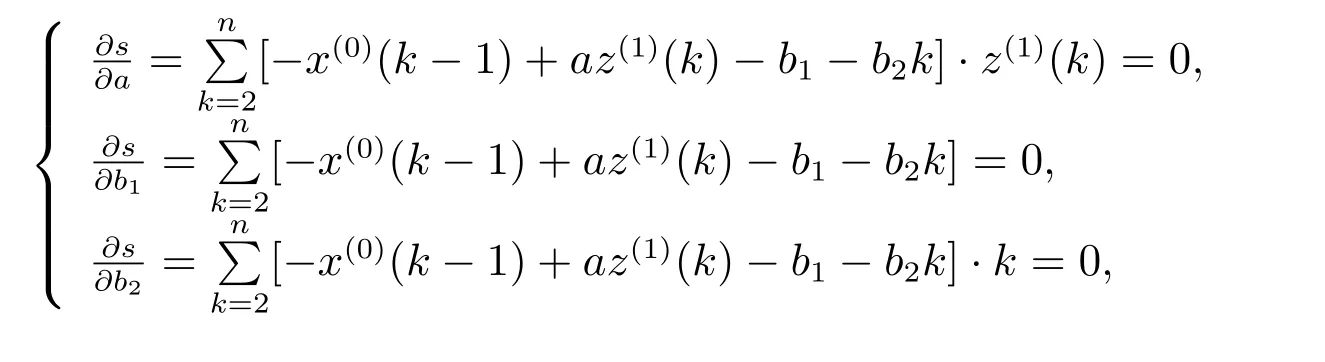
3.2 GOM(1,1)灰色预测模型背景值的优化

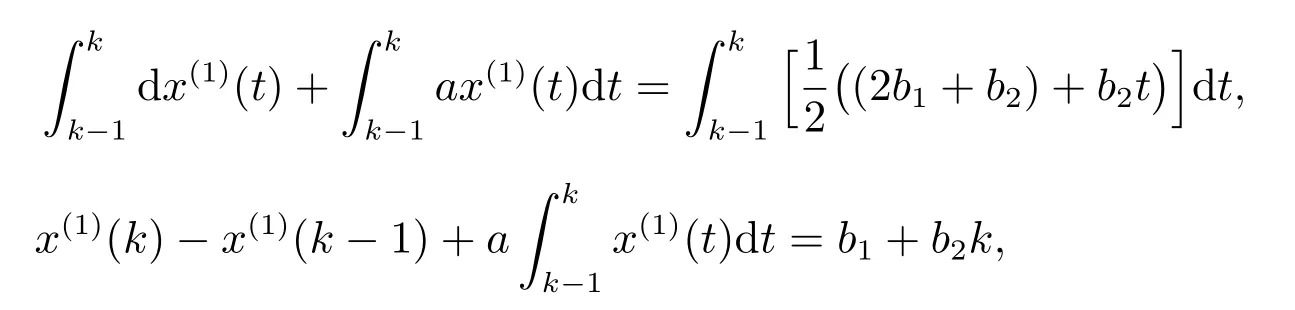
即

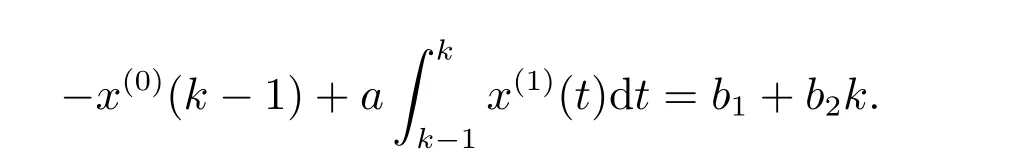
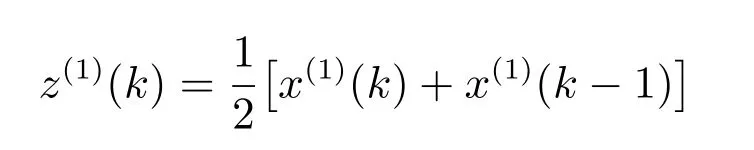
会具有更好的适应性.

定理3 x(0), x(1)如定义4 所示，若x(1)满足非齐次指数形式，则背景值为

其中k =2,3,··· ,n，且x(0)(k)/=x(0)(k-1).

证明 x(1)满足非齐次指数形式，不妨假设

x(1)(t)=AeBt+C,

其中A, B, C 为待定系数，背景值化简可得

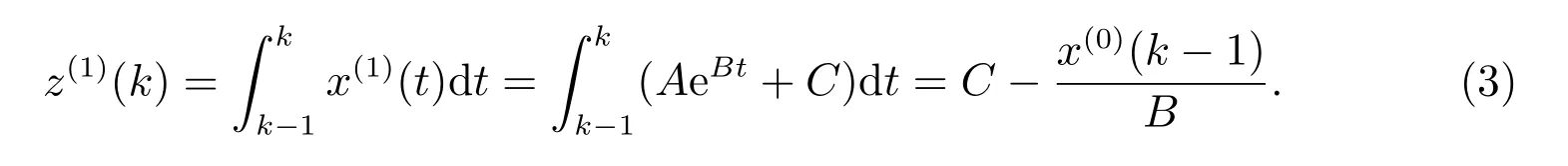
由于

则

从而

即

又由(4)式，可得

根据原始序列x(0)与一次反向累加生成序列x(1)的关系，当n = k 时，有x(1)(n) =x(0)(n)，即x(1)(n) = x(0)(n) = AeBt+C，得到C = x(0)(n)-AeBt，将(5),(6)式代入，则有

将(5)-(7)式代入(3)式整理可得定理结论.

3.3 初始条件的改进

传统GOM(1,1)模型选择初值时，认为拟合曲线一定通过点(1,x(1)(1))或(1,x(1)(n))，这种强制拟合曲线通过原始数据序列中的某个数据点的方法缺乏相应的理论基础，建立的模型预测误差较大.为了改进上述不足，本文以原始序列和模拟序列的平均相对误差平方和最小为原则[17]，确定时间响应函数中的最优常数C1.

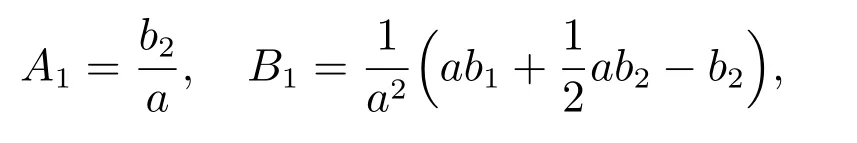
则

证明 边值条件未知时

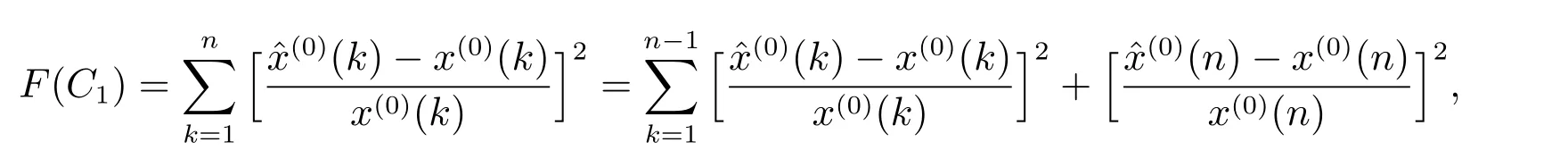
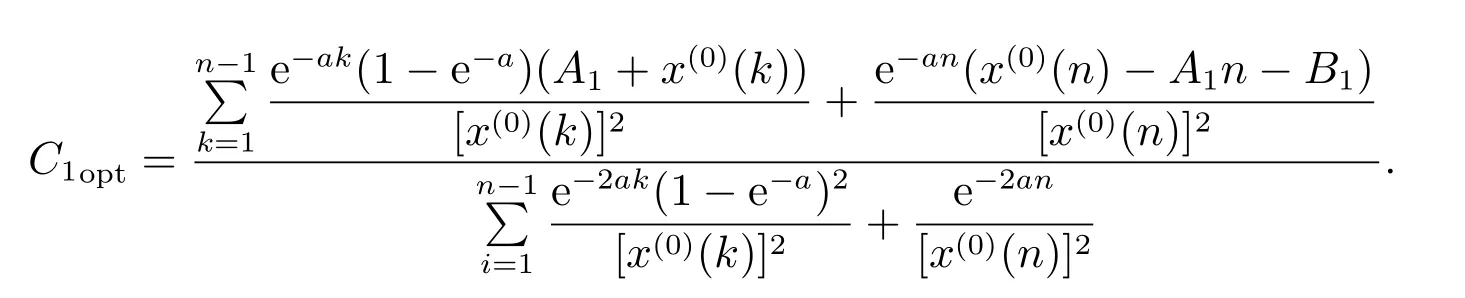
因此，改进GOM(1,1)模型的白化方程的时间响应式为

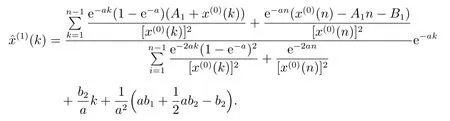
完整的GOM(1,1)模型改进算法如下：

② 根据定理4，构造指标函数F(C1)，确定最优常数C1；

③ 将①、②中的参数估计式代入累减还原式，可得序列还原值的估计值.

4 实例

一种害虫在某农药作用下单位面积内的数量随时间变化的采样数据，见表1[6].

表1 采样数据

设x(0)=(8,6.5,5.2,4.5,3.2)，一次反向累加生成序列x(1)=(27.4,19.4,12.9,7.7,3.2).传统灰色模型的时间响应式

文献[6]模型的时间响应式

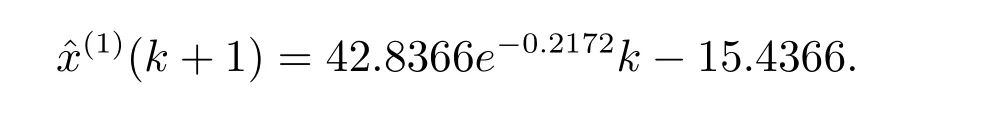
文献[7]模型的时间响应式

本文模型的时间响应式

从表2 的数据对比中可以看到，传统灰色模型的平均相对误差最大，说明使用累加生成方法处理具有递减趋势的数据序列，建模预测的适应性较差，导致建模误差较大；文献[6]提出了反向累加生成概念，由此建立了对于具有单调递减趋势序列的反向累加灰色GOM(1,1)模型，由于忽略了背景值的构造会影响建模精度，平均相对误差仅为1.67%；文献[7]发现了GOM(1,1)模型的缺陷，对背景值进行了优化，但却忽略了新背景值的建模适应性，导致对于本文实例中的数据序列建模效果不佳；本文优化模型的平均相对误差仅为1.17%，相对于其他几种模型的模拟精度有较大提升，能够说明改进算法后的新模型更有优势.

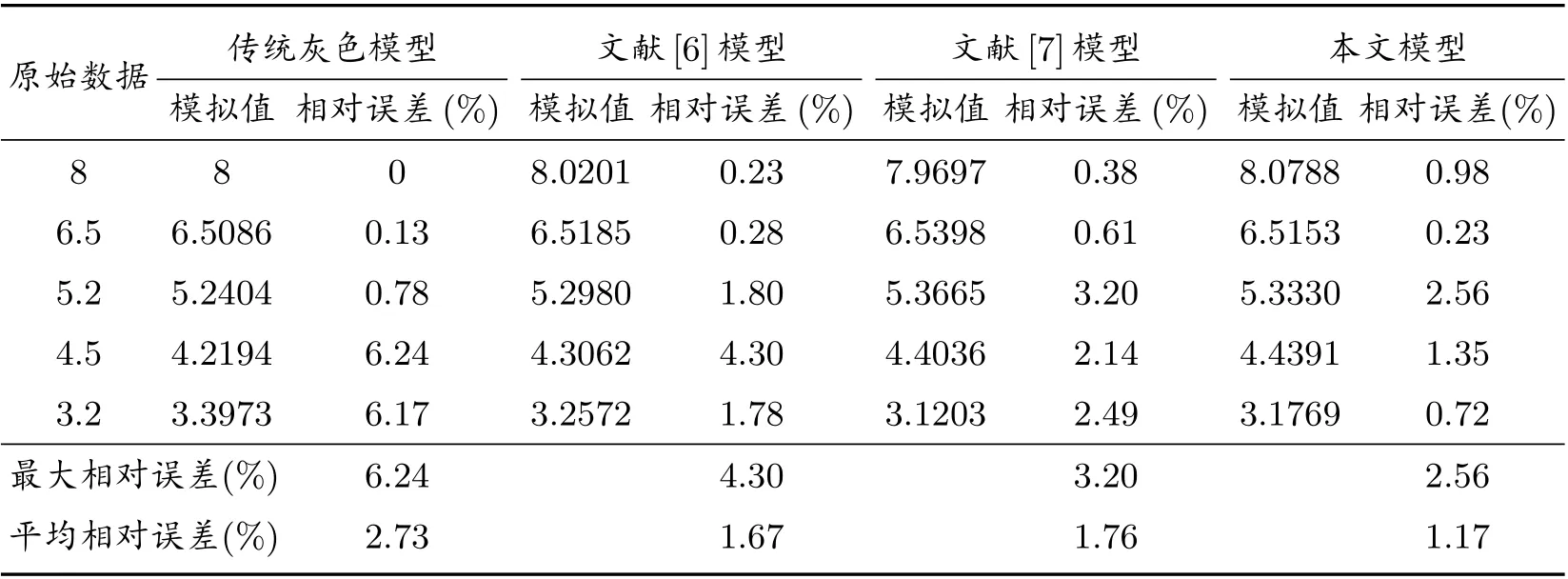
表2 四种模型的拟合结果和相对误差对比

关于模型精度的检验，采用精度检验等级的方法[1]来说明模型的优良性：

残差的均值、方差分别为

按照C 和p 的计算结果，参照表3 的具体指标对模型的精度进行评定.

表3 精度检验等级参考表

经过计算，本文模型的均方差比值为0.0422，小误差概率为1，根据表3 提供的精度检验等级参考表，模型精度等级为一级，表明该模型具有较高的模拟精度，可以用于中长期的预测.

5 结束语

本文从以下三方面提出了一个完整的GOM(1,1)模型改进算法：

1) 采用反向累加生成，考虑灰作用量的动态变化过程，建立了灰作用量的优化的GOM(1,1)模型；通过使用最小二乘法，得到了模型的未知参数估计式，并推导确定了时间响应函数的最优表达式；

2) 由背景值的几何意义，基于一次累加生成序列满足非齐次指数律的条件下，通过积分推导给出了GOM(1,1)模型的优化背景值，用以代替传统GOM(1,1)模型的背景值；

3) 以原始序列和模拟序列的平均相对误差平方和最小为原则，确定模型最优的初始条件，最终形成完整的GOM(1,1)模型改进算法.