基于广义g-h 分布模型的CVaR 估计及其应用研究

丁芳（宁夏师范学院）

■引言1

互联网的快速发展，虽然为我国金融领域发展开辟了新的道路，但是伴随着一定金融风险，如何准确测量风险成为当前重点研究内容[1]。目前，应用比较多的风险评估工具为VaR，由于此工具自身存在不足之处，需要进一步完善。通过查阅大量文献资料，CVaR 评估结构体系较VaR 有很大改善，扩大了资产损失估算范围，可以更为准确地反映金融风险[2]。本文选取广义g-h 分布模型作为研究工具，尝试探究CVaR 估计方法。

■广义g-h 分布模型

（一）g-h 分布定义

Maritine 等研究学者在学者Tukey 提出的g-h 分布定义基础上，探究g-h 分布特性，重新对g-h 分布进行了定义，从而更加精准地描述不对称现象。假设存在随机变量z～N( )1,0 ，那么可以得到随机变量的求解公式：

公式（1）中，X 服从g-h 分布，参数g 和参数h 均为常数，参数A 和参数B 均大于0。B 代表尺度，A 代表X 所处位置数据，g 代表分布模型的偏斜尺度，通过分析此数值变化规律，可知当前评估对象是否存在不对称特性，参数h 代表模型尾部变化特点，以正态分布尾部伸缩特点为准，描述尾部方向和大小。

（二）g-h 分布参数估计方法

目前，关于参数g 和参数h 的估计方法主要包括分位数估计法、极大似然估计法、矩估计法。其中，后两种方法计算量较大，评估体系比较复杂。相比之下，分位数估计法结构简单，计算量相对小一些，并且参数估计结果精准性较高，所以该方法得到了广泛应用。

假设X 的p 分位数用xp表示，其中，，假设Z 的p分位数用xp表示，其中，p 取值（0，0.5），两个分位数存在以下关系：

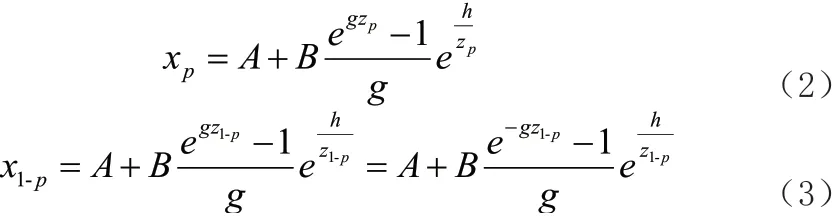
通过建立公式（2）和公式（3）之间的关联关系，可以得到不同样本条件下的分位数关系式：

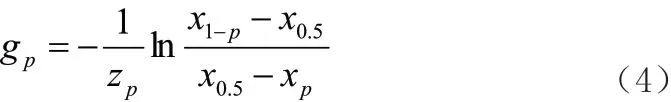
公式（4）中，替换样本分位数，便可以计算各项参数估计值。该公式中替换样本分别为1-p 和p，求取参数估计值为g。

依据公式（4）函数分布特点可知，当p 取值发生变化时，参数g 随之发生改变。为了准确估算数值g，本研究利用z 函数描述参数h 和参数g，并且要求描述函数均为偶函数。令参数g为)，参数h 为，经过计算分析得到关于g-h 分布的函数，即关于参数A 的估计公式：

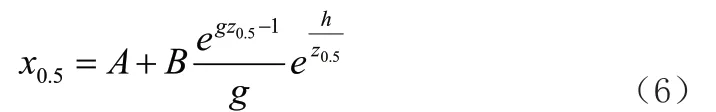
公式（6）可以利用中位数计算方法，求取估计数值A，而后将估算结果代入前几个公式中，可以求取和经过整理，可以估算出参数h 和参数B：

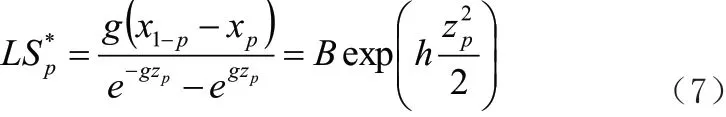
■基于广义g-h 分布模型的CVaR 估计

通过整理大量文献资料可知，采用VaR 估算金融风险，评估结果精准度偏低。之所以会出现此类情况，是因为该估算方法设定的风险范围较小，尤其是上限风险值过小，导致高风险评估未能融入其中。为了扩大VaR 估算条件均值范围，在此算法基础上扩大风险取值范围，提出CVaR 算法。该算法可以描述超额损失情况，上限值取值范围较大，可以用来分析超过VaR 算法值域以外的风险评估问题。为了更加准确地评估金融风险，本研究选取VaR 算法作为对照组，以CVaR 算法作为实验组，对比分析两种算法在金融风险估算中的性能。

（一）VaR 估计

关于VaR 算法的估计方法，首先需要设定置信度数值α。再次，采用g-h 分布函数，分别求取参数h、参数g、参数B、参数A。最后，利用蒙特罗方法求取VaR 估计结果。在此过程中，需要注意4 个参数计算是否准确，需要反复检验，否则VaR 估计结果将出现错误，影响算法可靠性判断结论。

（二）基于Monte-Carlo 模拟架构的CVaR 估计

关于CVaR 的估算，是在VaR 算法基础上增加了Monte-Carlo模拟处理，扩大了阈值范围，即添加了超出VaR 阈值部分。在应用模拟处理方法之前，设定置信度数值α。按照以下步骤完成CVaR 估算。

第二步：利用g-h 分布函数，统计金融投资项目的资产回报，分别求取n 取值不同情况下的资产回报值，计算结果记为

第三步：按照置信水平α取值情况，计算该分位数对应的资产回报数值，从而得到CVaR 估算结果。

■CVaR 估计方法在某证券市场综合指数评估中的应用

为了判断CVaR 估计方法是否可以提高VaR 估计方法精准度，本研究以某证券市场综合指数评估为例，利用两种方法分别估算，通过对比估算结果，做出准确判断。其中，综合指数为虚拟股票价格，利用Wind 咨询捕获相关数据，取2015.1.2 至2019.12.31相关数据作为样本数据，统计投资回报估算值。

（一）金融资产回报统计特征

关于投资回报估算结果用tR表示，计算公式如下：

公式（8）中，tP代表时刻为t 情况下的深证综指收盘价。通常情况下，金融资产回报存在不对称现象和尖峰厚尾性。当偏度计算结果大于0 时，认为收益率不对称。如果是峰度大于0，则表明当前回报分布尖峰厚尾现象较为凸出。分别利用CVaR 算法与VaR 算法，统计金融资产回报情况，结果如表1 所示。

表1 不同估算方法在金融资产回报中的应用计算结果

表1中统计结果显示，与VaR算法相比，CVaR算法标准差偏小，均值更加接近0，偏度和峰度更大。由此看来，CVaR 算法应用下，得到的偏度估算结果，能够更加显著的展示金融资产回报尖峰厚尾特点。与此同时，该算法估算下偏度展现出的收益率不对称特性更为显著。因此，在金融资产回报统计方面，CVaR算法优势更大。

（二）广义g-h 分布下的参数估计结果

为了对比CVaR 算法与VaR 算法在不同置信度条件下的金融风险估算值，本研究利用广义g-h 分布函数计算相关参数，将某证券市场样本数据代入函数中，求取各项参数数值，结果如下：

参数A 计算结果：-0.02188%；

参数B 计算结果：1.11869%；

参数h 计算结果：

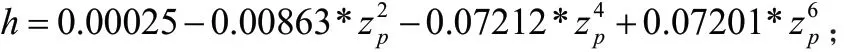
参数g 计算结果：

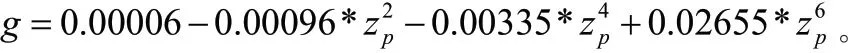
（三）不同置信度条件下的CVaR 与VaR 计算结果

本次应用研究，设定3 种置信度条件，分别估算这3 种条件下的CVaR 算法与VaR 算法的金融风险数值，结果如表2 所示。

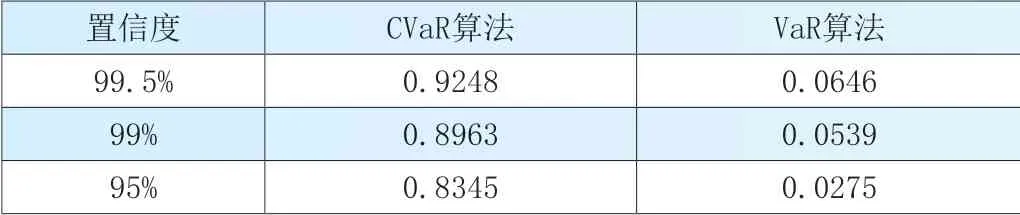
表2 不同置信度条件下CVaR算法与VaR算法的金融风险估算结果

表2 中统计结果显示，随着置信度的增加，金融风险估算数值随之增加，与VaR 算法相比，CVaR 算法数值更大一些。当置信度为95%时，VaR 算法估算的金融风险为0.0275，CVaR 算法估算的金融风险为0.8345；当置信度为99%时，VaR 算法估算的金融风险为0.0539，CVaR 算法估算的金融风险为0.8963；当置信度为99.5%时，VaR 算法估算的金融风险为0.0646，CVaR 算法估算的金融风险为0.9248。3 种置信度条件下，两种算法在95%置信度条件下的金融风险评估差值最大，CVaR 算法的优势更大，该算法可以捕获超过VaR 算法阈值范围情况下的金融风险，更适合应用于金融风险度量。

■总结

本文在VaR 算法基础上，提出了CVaR 算法，利用广义g-h分布模型求取两个算法涉及到的相关参数数据，为算法应用提供数据支撑。其中，CVaR 算法是在VaR 算法值域基础上进行了扩充，增加了超过VaR 算法值域的部分数据。实践应用结果表明，CVaR算法的金融资产回报估算结果更为显著，并且在不同置信度条件下都可以得到更为精准的金融风险评估结果。