基于直接模拟蒙特卡罗方法计算单一气体及二元混合气体的平均自由程

魏宁斐，冯 焱，孙雯君，成永军，董 猛，宋 伊，吴成耀，刘国庭

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

在真空技术中，混合气体广泛应用于生物医学[1]、航天器微型推力器[2]、分压力质谱计的校准等。但是对于混合气体条件下气体分子之间的碰撞过程研究较少（平均自由程、碰撞频率等）[3]，而研究混合气体分子平均自由程在工程上有很重要的意义，如通过对克努曾数的计算从而正确判断流动状态等。相比单一气体，混合气体分子之间的碰撞除了考虑气体的稀薄程度、压力和温度等参数外，还要考虑构成混合气体的组分以及各组分的浓度、混合物中每种组分的平均分子速度随混合物的平均分子速度以及宏观速度的不断变化等[4]。所以对于混合气体条件下分子之间碰撞过程的模拟要比对单一气体的模拟更复杂。

目前大多数模拟研究是针对单一气体分子内部相互碰撞过程的，运用的方法主要是分子气体动力学。Einwohner等[5]、Dongari等[6]使用硬球模型对气体分子的平均自由程和碰撞次数等微观量进行了模拟研究。李志刚等[7]研究了气体分子与纳米粒子的碰撞过程，进一步研究了漫反射在气体分子与纳米粒子碰撞中产生的原因。何格等[8]利用Matlab对理想气体下气体的平均自由程等进行了模拟计算，并验证了其算法中速度分布遵从麦克斯韦速度分布。李海涛等[9]基于分子气体动力学方法，利用C语言自编模拟程序，对空气的平均自由程、自由程分布等进行了模拟研究。相比分子动力学模拟方法，直接模拟蒙特卡罗方法也常被人们用来研究分子的运动、碰撞以及与壁面的相互作用[10-12]。直接模拟蒙特卡罗法首先由澳大利亚的Bird[10]提出，其基本原理是用大量的模拟分子模拟真实的气体分子，每个模拟分子通常代表相当数量的真实分子，须对分子的碰撞与运动进行解耦。White等[13]也运用直接模拟蒙特卡罗方法对O2在单位时间单位体积内的碰撞次数进行了模拟计算，并与理论计算进行比较，其结果一致性较好。直接模拟蒙特卡罗方法还被广泛应用于低地球轨道和深空中的卫星和航天器的模拟、返回舱进入大气的模拟、太空环境下喷嘴和喷头射流的模拟、微尺度流动的模拟和快速非平衡的气体流动的模拟（激光烧蚀、蒸发、沉积）及全球大气评估等方面[14-17]。

但是，这些模拟工作普遍存在两方面的问题，其一，多数研究的是单一气体分子的平均自由程，且对于气体分子之间的碰撞处理均选用传统的硬球模型（HS），即未考虑气体分子的直径是随着其相对速度不断变化这一现实因素；其二，多数是对单一温度下碰撞过程进行研究，未考虑宽温度区间不同模型模拟结果的差异性。针对上述不足，本文采用直接模拟蒙特卡罗方法，选用可变硬球模型（VHS）以及可变软球模型（VSS），分别对单一及二元混合气体在平衡态下分子间的碰撞过程在温度为300～20 000 K间进行模拟研究，通过理论计算验证模拟结果的准确性。同时将两种模型下的模拟结果与HS的计算结果进行比较。

1 物理模型

1.1 模拟空间模型的建立与边界条件设置

为了模拟空间中单一气体及混合气体在平衡状态下内部分子的运动与碰撞的微观过程，包括分子单位时间单位体积内的碰撞次数、平均自由程等，本次模拟建立了一个边长为0.027 m，体积为1.96×10-5m3的正六面体计算区域，整个计算区域为一个网格。本文模拟的分子数密度对于单一气体及二元混合气体均为1×1019个/m3，其中每个分子代表真实分子个数为2×108个。模拟时间步长为10-7s，总共模拟1 000个时间步长，模拟时间为10-4s，这样设置的依据是用硬球模型下平均自由程计算公式对模拟分子质量最小的N2进行计算，其平均自由程约为0.160 m，同时模拟时间步长也可用N2的平均自由程与其最大平均速度（20 000 K）之比即1.2×10-4s，该值小于平均碰撞时间。另外采用无时间计数器（NTC）碰撞处理方法，可完全避免采用传统时间计数（TC）方法时出现的问题，即在特别强激波前缘等高度非平衡情况下，概率与时间上间隔的关联带来的问题，偶然接收的小概率的碰撞可能导致网格时间往前推进很长一段，以至于很多时间步长内无碰撞计算。

模型初始化时，在模拟空间中产生一定数量的模拟分子，每个模拟分子代表一定数量的真实分子。直接模拟蒙特卡罗方法首先以随机数的方式在模拟空间里生成每个模拟分子的初始位置坐标，遵从麦克斯韦速度分布的初始速度，如式（1）所示：

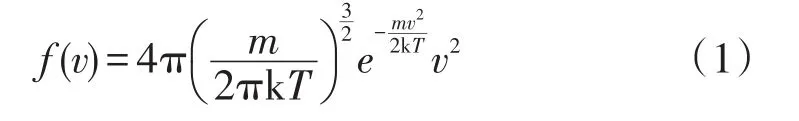
式中：v为气体分子运动速度，m/s；k为玻耳兹曼常数，J/K；m为气体分子质量，kg；T为模拟温度，K。

初始化温度为300～20 000 K。图1所示为本文模拟的物理模型，即单一或者混合气体初始化后气体分子空间分布图。

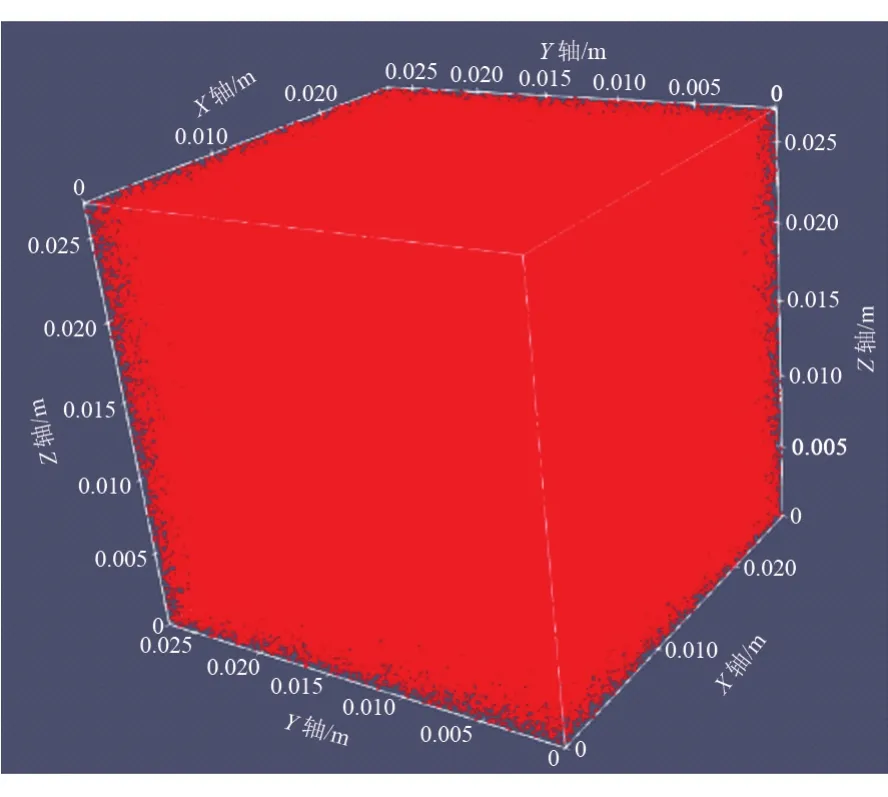
图1 模拟空间模型中的气体分子三维空间分布图Fig.1 Three-dimensional spatial distribution map of gas molecules in simulated space model

壁面边界条件采用周期性边界条件，这样设置可以消除由于粒子进入和离开表面所引入的表面效应和边界效应。本文对正六面体计算域的壁面温度均设置为300 K。相比于传统的气体分子动力学模拟方法，其存储和参与运算的数据量相对比较小，在相同的模拟空间模拟相同的分子数时，运算时间大幅减小，模拟更接近于平时所遇到的情况，即分子数密度较大，模拟结果的准确性高，重复性好。

1.2 二元碰撞模型

模拟过程中，气体分子之间的碰撞采用VHS[18]。这是因为传统硬球分子具有固定不变的截面，而真实分子的碰撞截面是随着相对速度的不同而改变的（随着相对速度cr的增加而减小，同时随着相对平动能εt的增大而减小）。这是模拟真实气体流动过程中必须要满足的条件。这样能保证气体黏性系数μ与温度T的关系和实际气体一致，而不是传统硬球模型下黏性系数μ与温度T所呈现的线性关系。VHS模型假设分子具有硬球一样的均匀散射概率，这使得计算碰撞后速度的取样十分简单。分析和数值研究的实际应用表明，分子的散射概率可观测到的变化很小[18]。

令碰撞截面正比于相对速度的逆幂次。引入总碰撞截面σT、分子直径d、相对速度cr和相对平动能量εt=mrcr2/2 的参考值：σT，ref、dref、cr，ref和εt，ref，其中σT，ref、dref是相对速度为cr，ref时的值，可以定义VHS模型为：

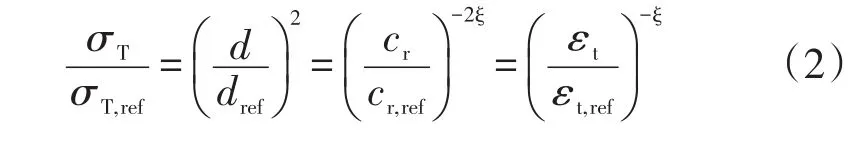
其中：ξ是碰撞截面σT依赖于相对速度cr、平动能量εt的规律中的方幂，其值为常数。并且VHS模型散射角与硬球模型的规律相同。

同时也利用VSS模型做了对照模拟，VSS模型与VHS模型的不同之处在于考虑了动量截面与黏性截面的比。其直径变化方式与VHS模型相同，但其散射角为：

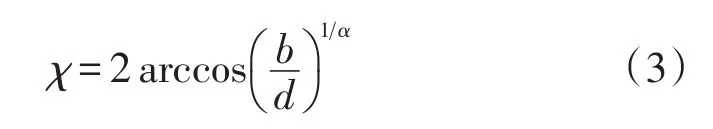
式中：b为瞄准距离，即质心坐标系中，尚未受到两分子相互作用力影响的分子轨道间的最接近距离；d为气体分子直径；α为散射系数，其值一般在1～2之间。

1.3 不同二元碰撞模型下单一及混合气体相关量计算

气体分子自由程是克劳修斯于1859年提出的，其物理意义是一个分子相继两次碰撞之间所通过的路程。对于单一气体，其分子平均自由程可以运用基于分子速度分布规律推导的式（4）方便地计算：

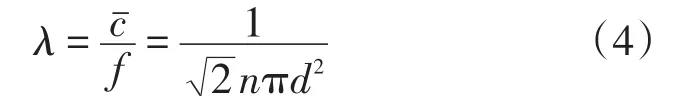
式中：λ为分子的平均自由程，m；为分子平均热运动速率，m/s；f为碰撞频率，次/s；n为分子数密度，m-3；d为气体分子直径，m。

当扩展到混合气体时，由于其各组分的摩尔质量不同导致了热运动速度的多样性和复杂性，即每种组分不但有相对于自己组分的速度还有相对于其他组分的速度。这也给混合气体的平均自由程计算带来了挑战。因为混合气体分子平均自由程是由分子之间的相对速度、平均碰撞截面、热运动速度等决定的。假设混合气体由p组分和q组分构成，可选取p组分分子作为测试分子，将q组分分子视为场分子。因此混合气体中p、q两组分分子之间的碰撞频率为：

p组分分子的碰撞频率可以通过对所有组分的碰撞求和得到，即：

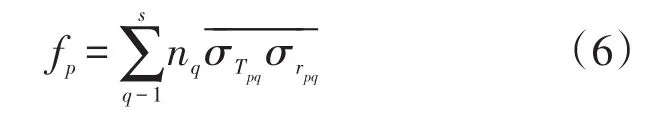
所以p组分分子的平均自由程等于该组分的平均热运动速率除以碰撞频率：

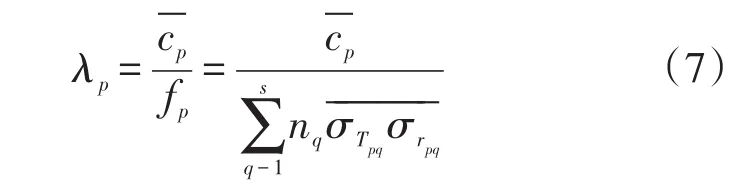
混合气体分子平均自由程则可写为：

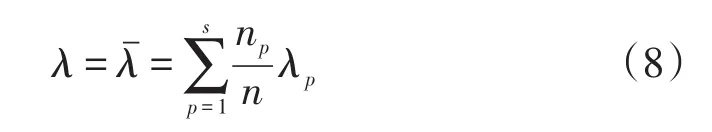
方程式（5）～（8）只是混合气体碰撞频率和平均自由程的一般结果，即将分子作为传统硬球模型来考虑。对于可变硬球模型（VHS），考虑s种VHS分子组成的混合气体，则当混合气体处于平衡状态时，则其中p分子与所有q分子之间的碰撞频率可以写成式（9）：

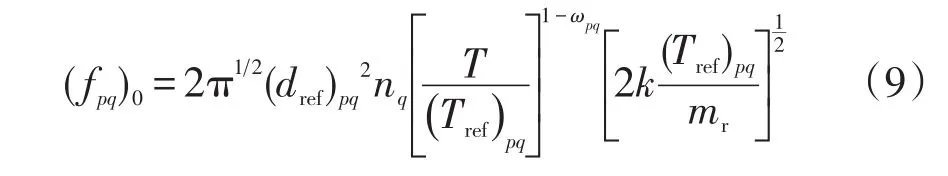
式中：dref为气体分子参考直径，m；T为温度，K；mr为折合质量，kg；ωpq为p、q分子的黏性系数；Tref为参考温度，K。

由式（6）可得组分p的碰撞频率：

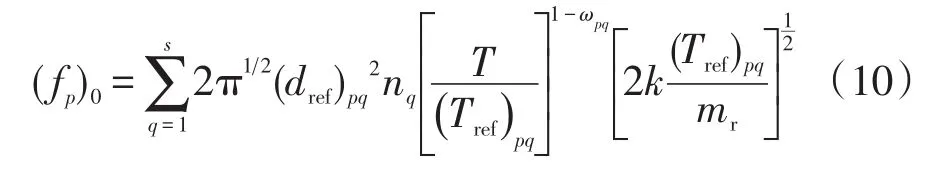
则混合气体组分p的平均自由程等于其平均热速率除以其碰撞频率，可得：

最后，混合气体的全局平均自由程为：

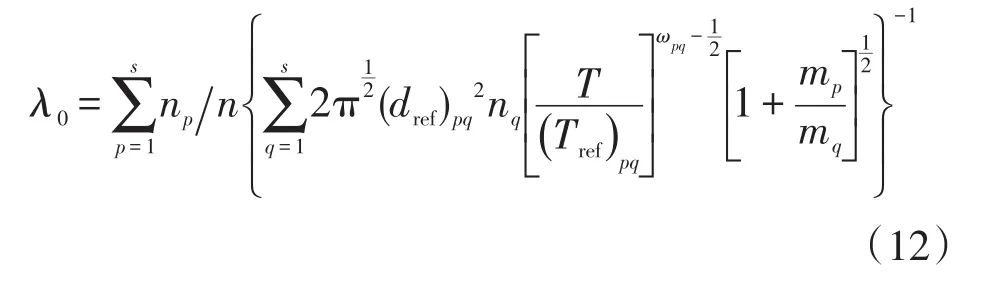
式中：mp为p分子质量，kg；mq为q分子质量，kg；

因此，对于混合气体来说，要想准确获取克努曾数进而计算出其流态较为困难。更进一步分析所要用到的一个结果是当混合气体处于平衡状态时，平衡气体中p组分和q组分之间单位时间单位体积内的碰撞次数，即：

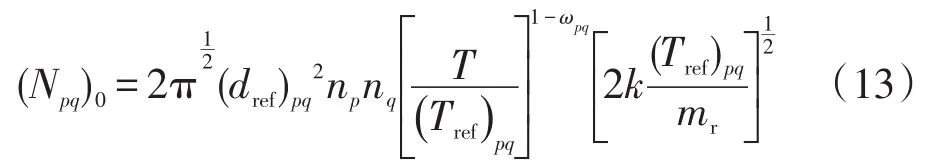
当式（12）、式（13）中的ωpq=1/2时，可用作计算HS下混合气体分子平均自由程及p组分和q组分之间单位时间单位体积内的碰撞次数。而对于VSS来说，其相关量的计算方法和VHS计算方法相同，只是其在273 K时气体分子的参考直径不同。

2 模拟流程

本文依据Bird提出的直接模拟蒙特卡罗方法，运用开源软件OpenFOAM-2.4.0-MNF中的dsmc⁃Foam+对单一及二元混合气体在平衡状态下的微观量进行了模拟。选取模拟时间作为总体循环控制变量，模拟时间步长一般小于分子之间的平均碰撞时间，在每一个时间步长∆t内，首先认为分子按照平衡状态时麦克斯韦速度分布做匀速直线运动，然后判断其是否与壁面发生碰撞，若与壁面发生碰撞，则按照壁面边界条件设置，本文壁面边界条件为周期性边界条件，即粒子到达壁面后消失，然后按照原速度从相对的壁面中发射出来。当分子运动到新的位置时，更新分子位置坐标并记录其速度大小、方向等量，按照一定的顺序对模拟分子重新编号。然后，在每个网格中按照接收-拒绝原则判断分子间是否发生碰撞，若分子之间发生碰撞，按照本文所选择的VHS模型或者VSS模型计算碰撞后的速度和内能等。当模拟时间达到设定值后，跳出循环，自动结束本次模拟并对流场性质进行抽样得出总的碰撞次数、平均自由程等值，同时也可以对模拟空间内的压力进行统计。具体流程如图2所示。

图2 直接模拟蒙特卡罗方法流程图Fig.2 Direct Simulation Monte Carlo method flow char

3 结果与分析

建立了长宽高均为为0.027 m，体积为1.96×10-5m3的正六面体模拟空间模型如图1所示，并对N2、O2、Ar等单一气体，以及N2∶O2、Ar∶O2、Ar∶N2分别为1∶1的混合气体的分子平均自由程、单位时间单位体积内的碰撞次数等在模拟温度为300～20 000 K之间进行了模拟计算（具体参数如表1和表2所列，其中表2中的数值可由参考文献[18]查得），并将模拟计算结果与上述VHS模型理论计算结果相比较，验证模拟方法和模拟结果的准确性。同时设置了在VSS下，单一气体N2和N2∶Ar为1∶1时的平均自由程、单位时间单位体积内的碰撞次数随着温度变化的对照模拟。并将上述两种模型的模拟结果与传统硬球模型的结果进行对比，比较三种模型下结果的差异。

表1 单一及混合气体分子数密度及模拟时间Tab.1 Single and mixed gas number density and simulation time

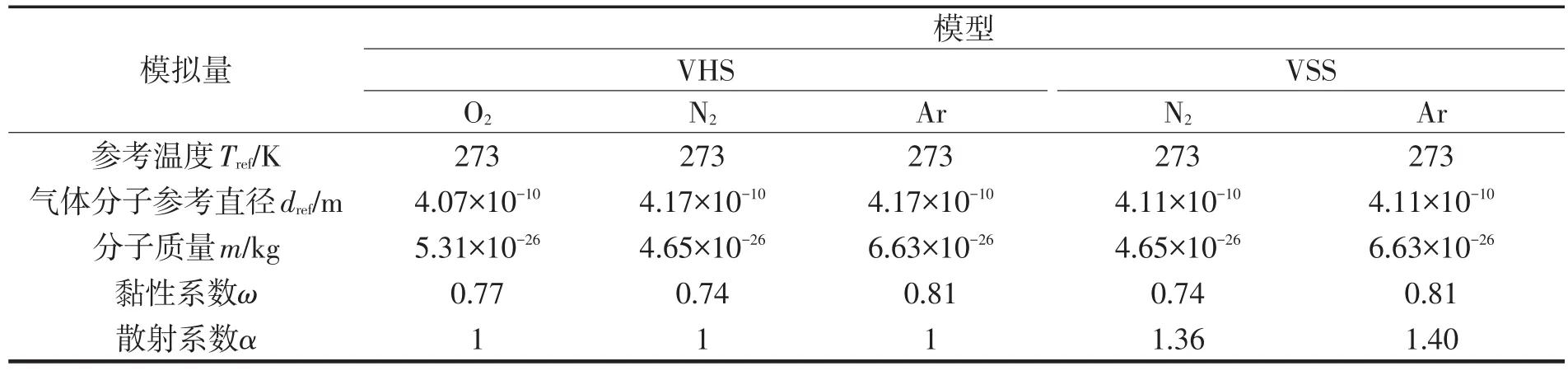
表2 不同模型下模拟分子特性Tab.2 Simulated molecular properties at different models

3.1 气体分子自由程测试

统计了单一气体以及二元混合气体在不同温度下模拟空间内气体分子的平均自由程，并与VHS模型下混合气体全局平均自由程计算式（12）的理论计算结果进行比较，如表3所列，从表中可以看出，随着温度的升高，单一气体及二元混合气体的平均自由程均增大，这是由于温度升高其热运动速度增大从而使其碰撞截面减小所致。对于单一气体，其相对偏差很小，最大只有0.08%，且随着模拟温度的升高没有明显变化。对于二元混合气体，其模拟值和计算值之间的相对偏差与混合气体两组分相对分子质量差值有关，当两组分的相对分子质量差越小时，其模拟值与计算值越吻合。但是当两组分相对分子质量相差较大时，如Ar∶N2=1∶1时模拟值与计算值之间的相对偏差较大，引起这种现象的原因是轻分子的碰撞具有较大的相对速率，而且这个相对速度要用在(σTcr)max中，于是较轻的分子接受率要高于较重的分子。

表3 VHS模型下单一及二元混合气体分子平均自由程理论计算与模拟值比对表Tab.3 Simulation and calculated mean free path of pure and binary gas mixture at VHS model

本文还利用VSS模型对N2及N2与Ar的混合气体的平均自由程进行了模拟计算，并利用式（12）进行了理论计算，详细计算结果与模拟结果的对比如表4所列。并与用HS计算的结果进行对比，如图3和图4所示，发现在HS下分子数密度相同时单一及混合气体分子平均自由程在宽温度区间有很大的误差，这是由于HS的分子直径是一个定值，不随温度变化。而对于VHS和VSS而言，考虑了分子直径随着温度升高会变小这一现实情况，其平均自由程随着模拟温度的升高而增大。但是可变软球模型的值要更大，是因为其考虑了动量截面与黏性截面之比，从文献[19]中可知，N2、O2在VSS模型下黏性系数值在温度为300～15 000 K间与实验数值符合很好，所以VSS模型与真实气体条件更接近。因此，本文中VSS模型下平均自由程模拟结果应更符合实际情况。

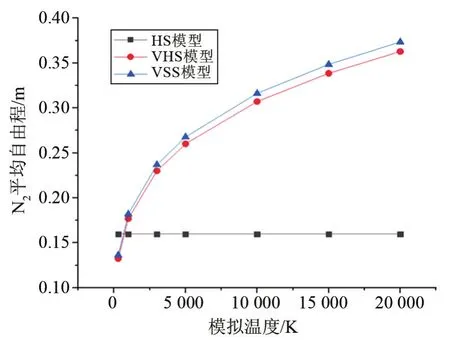
图3 N2在不同温度不同模型下的气体分子平均自由程Fig.3 The mean free path of N2under different temperatures and different models

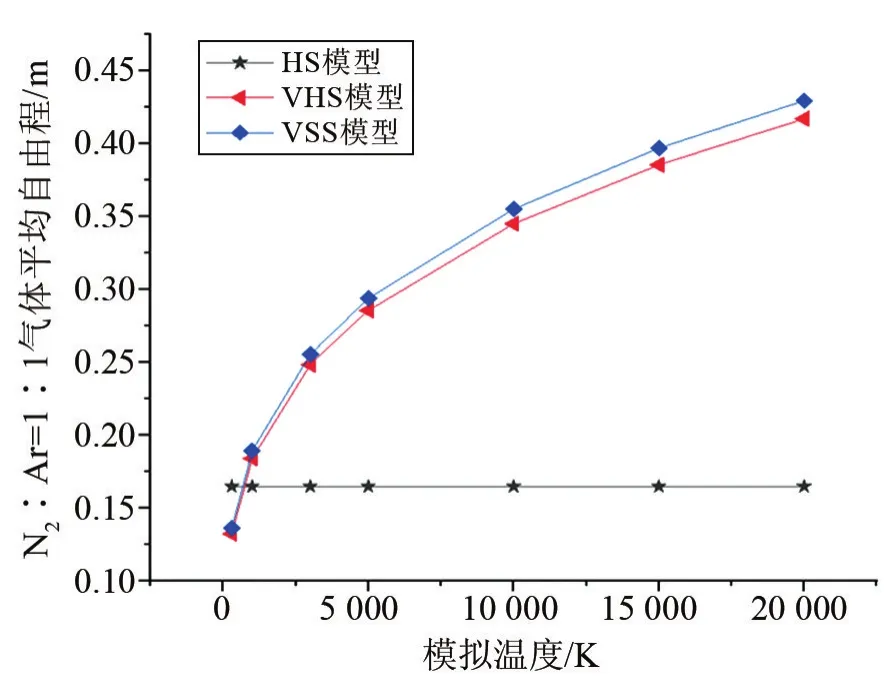
图4 N2∶Ar=1∶1在不同温度不同模型下的气体分子平均自由程Fig.4 The mean free path of N2∶Ar=1∶1under different temperatures and different models

表4 VSS模型下单一及二元混合气体分子平均自由程理论计算与模拟值比对表Tab.4 Simulation and calculated mean free path of pure and binary gas mixture at VSS model

3.2 气体分子碰撞次数测试

表5统计了三种单一气体以及三种混合气体在总的分子数密度不变时VHS模型下单位时间单位体积内的碰撞次数随模拟温度的变化关系。表6对单一气体N2和N2∶Ar=1∶1的混合气体在VSS模型下进行了对照模拟。

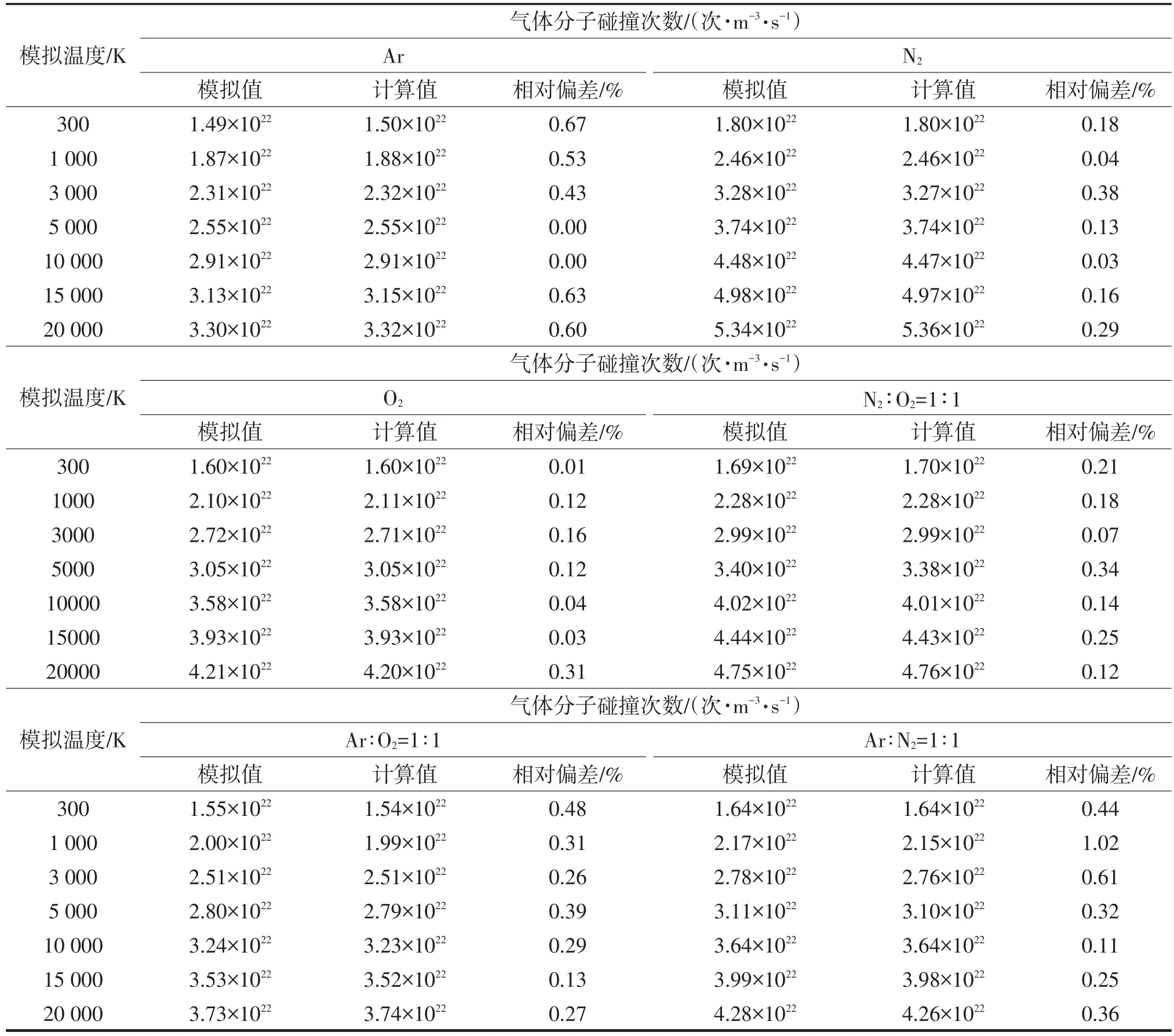
表5 VHS模型单一气体及二元混合气体单位时间单位体积内分子的碰撞次数Tab.5 Simulated collision rates compared with analytical values for pure and binary gas mixtures at VHS

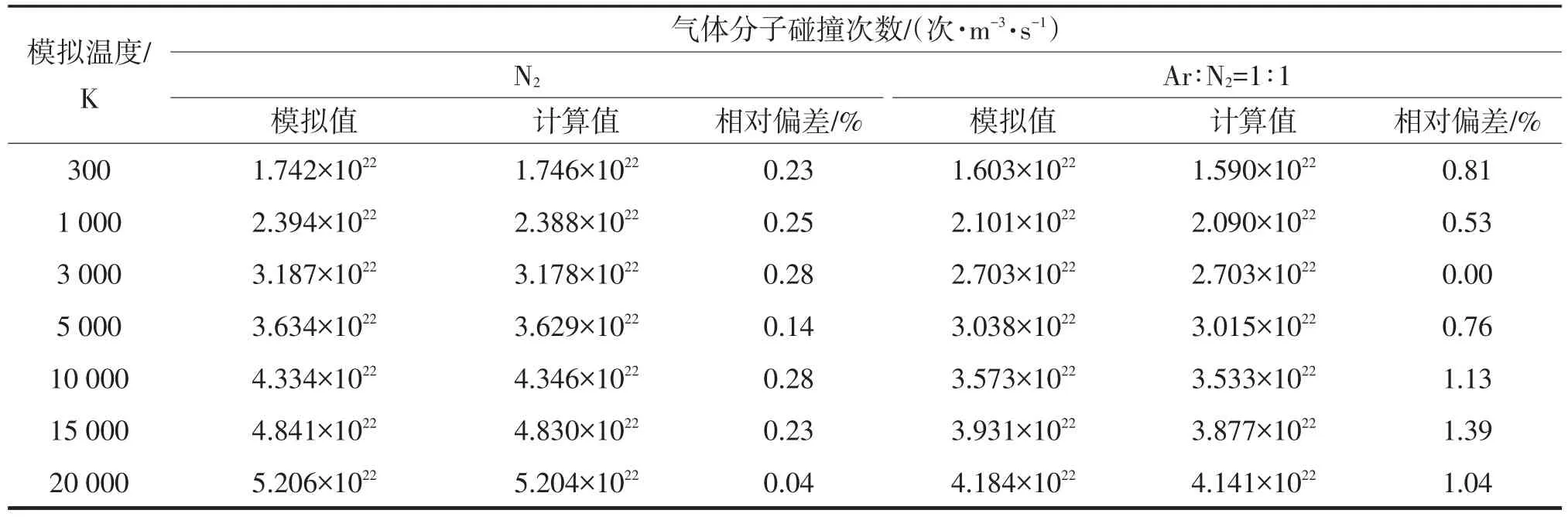
表6 VSS模型单一气体及二元混合气体单位时间单位体积内分子的碰撞次数Tab.6 Simulated collision rates compared with analytical values for pure and binary gas mixtures at VSS

运用式（13）分别对VHS和VSS两种模型下单位时间单位体积内的碰撞次数进行了计算，并对模拟值和理论计算值进行了比较，由表5及表6可看出，理论值与模拟值相差不大，在概率波动范围内。在同一模型下其单位时间单位体积内总的碰撞次数与单一气体的分子质量或者与混合气体的折合质量有关，即在相同的分子数密度、相同的温度条件下，其单位时间单位体积内碰撞次数随着分子质量或者折合质量的减小而增大。在相同的分子数密度下，同种气体分子之间的碰撞次数随着温度的升高也不断增大，这种现象符合布朗运动的特征。

将传统HS的计算结果（其计算方法是令式（13）中的ωpq=1/2，且dN2=3.754×10-10m，dAr=3.628×10-10m）与VHS和VSS两种模型下的模拟结果进行比较，具体如图5图6所示。对于单一气体及混合气体，其HS的结果与温度的二分之一次方成正比，当模拟温度大于300 K时，其值大于VHS和VSS的结果。其大小从VSS到VHS再到HS由小变大，这说明VHS模型考虑了真实的分子碰撞截面是随着相对速度的不同而改变，黏性系数随温度不同也接近于真实气体，VSS模型除了VHS所考虑的因素外还考虑了动量截面与黏性截面的比，使得其结果更接近于真实条件，所以在混合气体条件下，利用VSS更加准确[18]。

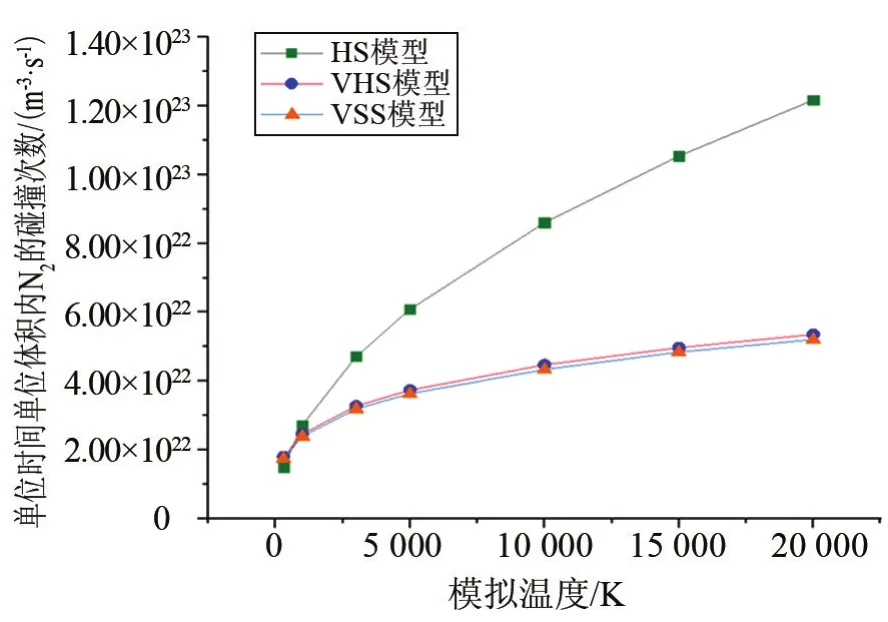
图5 N2在不同模型下单位时间单位体积内分子碰撞次数Fig.5 Collision rates of N2at different models

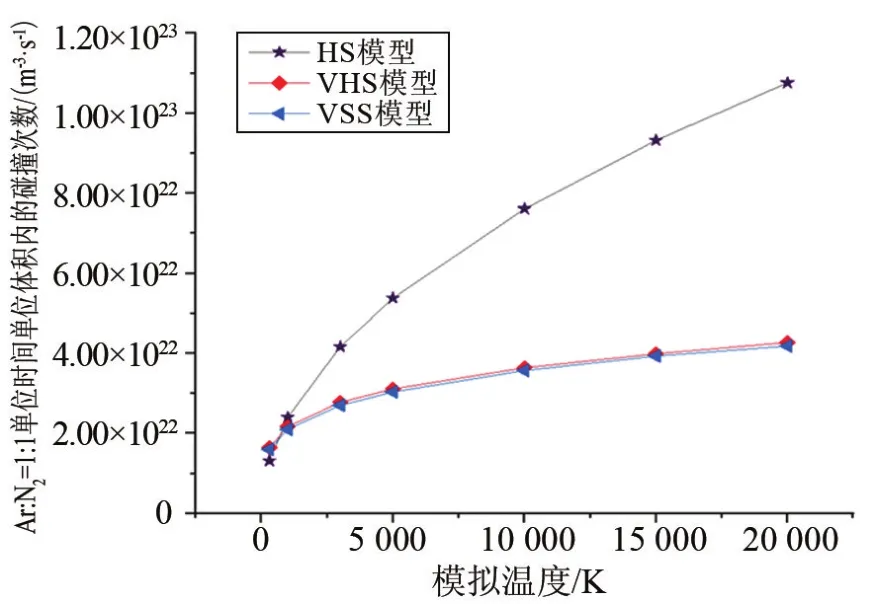
图6 Ar∶N2=1∶1在不同模型下单位时间单位体积内分子碰撞次数Fig.6 Collision rates of Ar∶N2=1∶1 at different models

从模拟结果与计算结果之间的相对偏差可知，针对单一气体及二元混合气体在平衡状态下气体分子间碰撞过程的直接模拟蒙特卡罗方法是准确的。相比于利用分子动力学模拟计算平均自由程的方法，直接模拟蒙特卡罗方法所用的模拟时间更短、单一气体的模拟计算精度更高，李海涛等[9]对空气模拟计算的相对误差最大为12.1%。能够用来计算混合气体的全局平均自由程，只要混合气体组分间相对分子质量相差较小，其相对偏差不超过0.8%。相比于何格等利用传统HS对He在298 K时平均自由程的模拟，本文对分子之间的碰撞处理运用了VHS及VSS，模拟温度为300～20 000 K。同时对二元混合气体情况下的分子平均自由程、单位时间单位体积内的碰撞次数也进行了模拟计算，因此对处理两种及两种以上混合气体全局平均自由程具有指导及借鉴意义。

4 结论

对于单一气体，气体分子平均自由程及碰撞次数的模拟结果与理论计算结果的相对偏差很小，对于相对分子质量接近的二元混合气体，其相对偏差亦很小。随着两组分相对分子质量之差变大，模拟与计算值的相对偏差也变大，验证了VHS及VSS、壁面周期性边界条件设置、模拟分子数密度1×1019m3等条件下利用直接模拟蒙特卡罗方法的可行性与准确性。将VHS与VSS的模拟结果与HS的计算结果进行比较，发现HS下的气体分子的平均自由程在宽温度区间有较大误差，气体分子碰撞次数在模拟温度大于300 K时也远高于其他两种模型的结果。所以在处理较高温度时气体分子之间的碰撞过程选用VHS或者VSS，结果会更准确。在分子水平研究了单一及二元混合气体的碰撞过程，为后续二元混合气体在总分子数密度相同下，按照不同比例混合时气体的平均自由程、单位时间单位体积内的碰撞次数模拟研究，以及更多组分的混合气体模拟研究提供基础。有助于解决一些实际工程问题，例如通过计算混合气体全局平均自由程从而对混合气体克努曾数进行计算，进而能准确判断气体的流动状态。