以“不变”应“万变”
——2020年全国Ⅰ卷的两道动态类题
2021-03-29何彦雨李富恩
何彦雨 李富恩 陈 菁
(1. 北京林业大学理学院,北京 100083; 2. 澳门城市大学教育学院,澳门 999078;3. 华北油田第三中学,河北 任丘 062552)
1 原题呈现
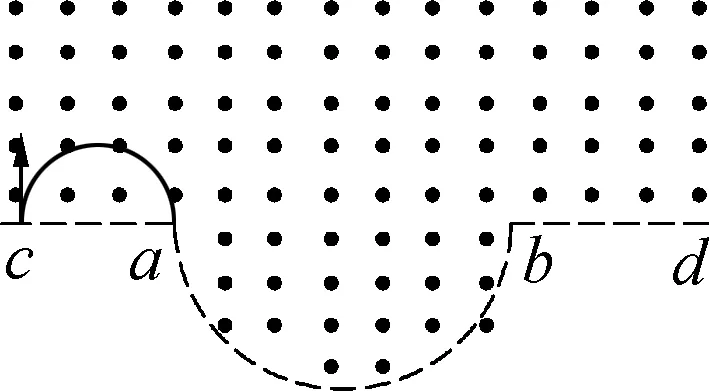
图1 2020年全国Ⅰ卷18题图
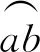
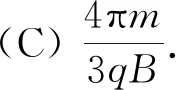
答案: (C).
2 动态图解法探析
粒子仅受洛伦兹力,在磁场中做匀速圆周运动,
可得粒子在磁场中运动的周期为
设粒子在磁场中运动的时间为t,则有
则对于给定的粒子在磁场中运动的时间与速度无关,仅由圆心角决定,轨迹对应的圆心角θ越大,运动的时间就越长.笔者通过改变圆的半径来解决该问题,粒子垂直ac射入磁场,轨迹圆心必在ac这条直线上,现将粒子的轨迹半径由0逐渐放大分别进行讨论.
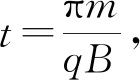
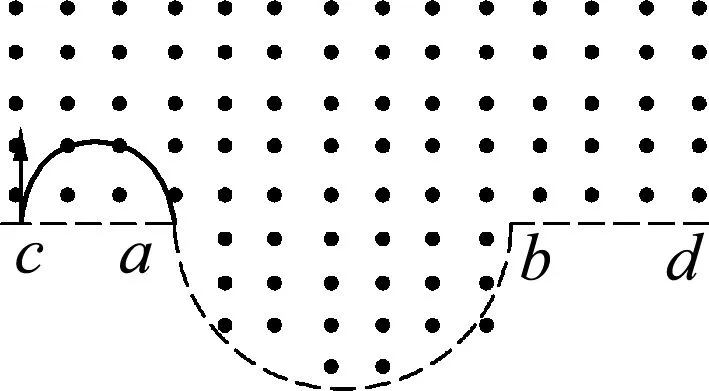
(a)
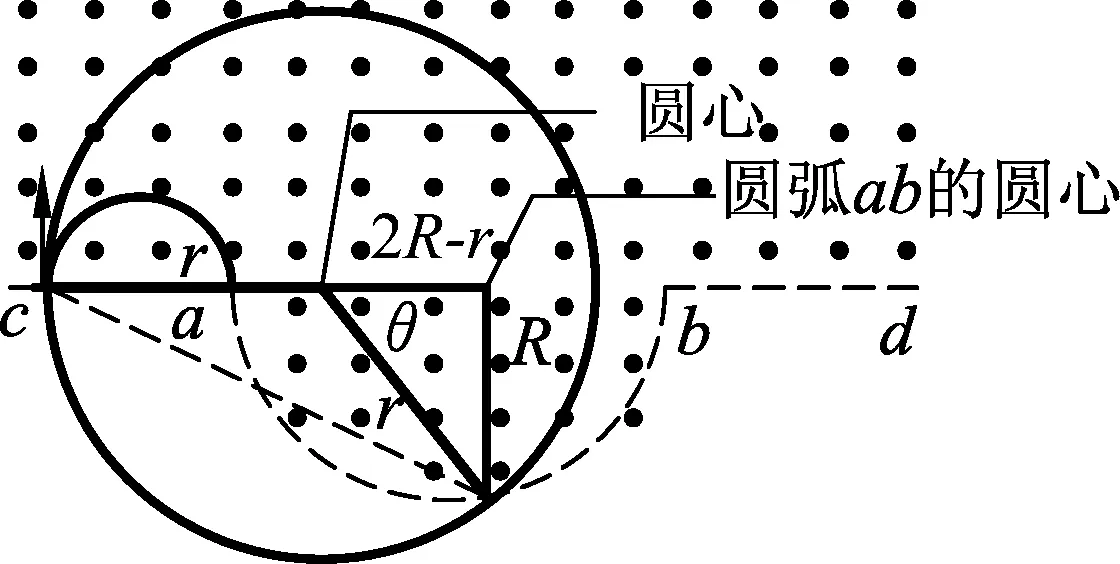
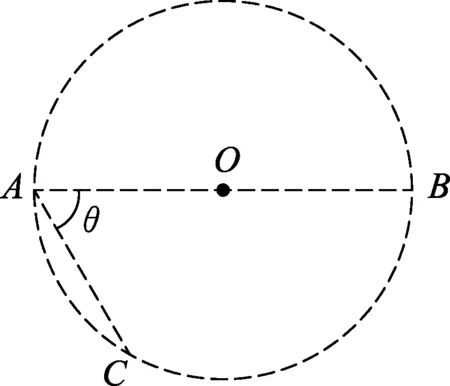
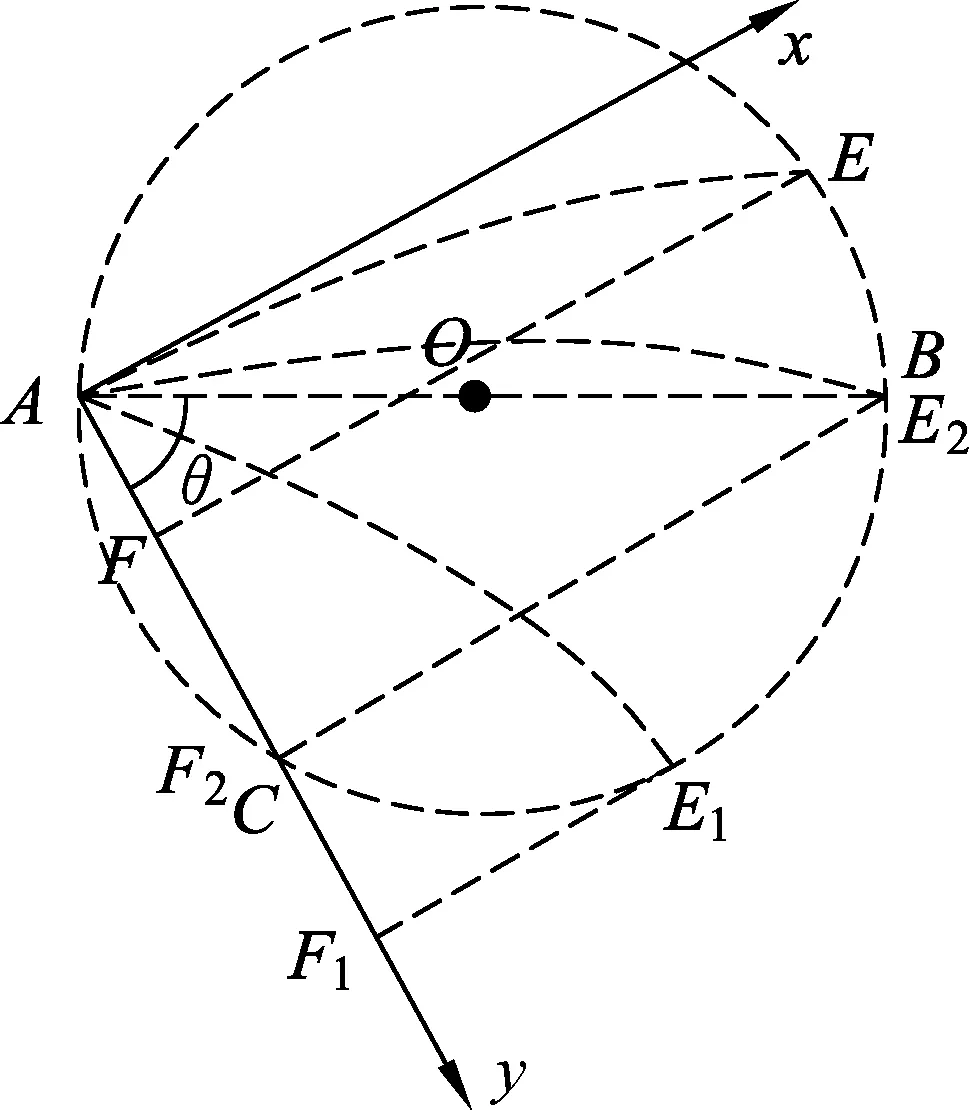
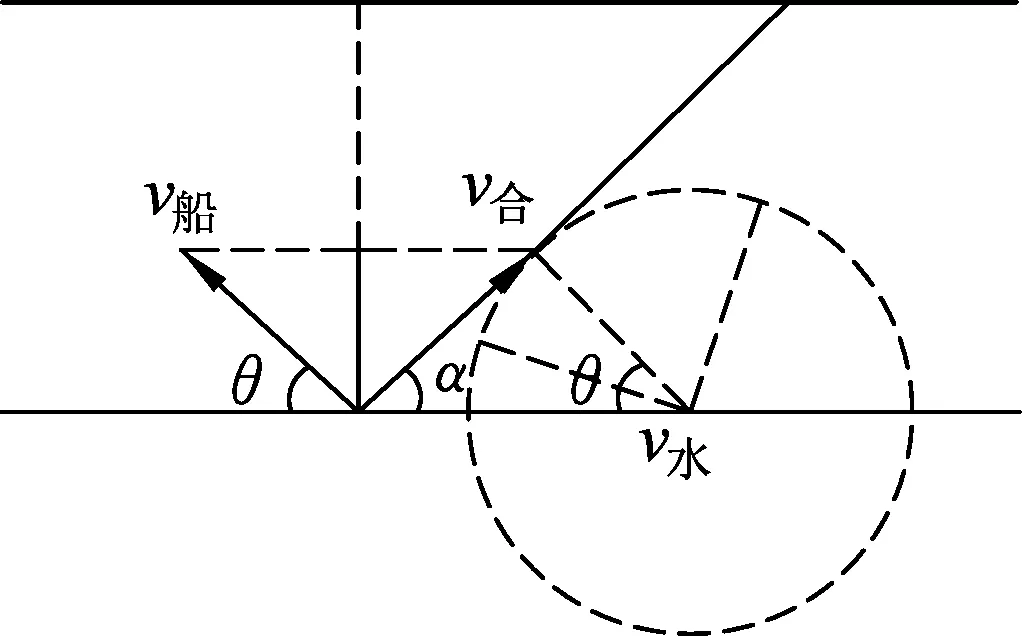
当0.5R 粒子运动最长时间为 故选(C). 图3 当0.5R 另外,在解答本题时如果没有考虑到“动态图”的几何解题方法,那么采用较为常规的代数方法来求解函数极值的亦可,利用余弦定理来求得此题目中函数极值确定时间最长时的轨迹圆心位置. 图4 运动轨迹各边角示意图 如图4所示,由余弦定理可得 R2=r2+(2R-r)2-2r(2R-r)cosθ. 化简可得 所以,当r=R时上列式子有最小值,即θ有最大值.因此当轨迹半径等于R时轨迹圆心角最大. 图5 2020年全国Ⅰ卷25题图 (2020年全国Ⅰ卷第25题)在一柱形区域内有匀强电场,柱的横截面积是以O为圆心,半径为R的圆,AB为圆的直径,如图5所示.质量为m,电荷量为q(q>0)的带电粒子在纸面内自A点先后以不同的速度进入电场,速度方向与电场的方向垂直.已知刚进入电场时速度为0的粒子,自圆周上的C点以速率v0穿出电场,AC与AB的夹角θ=60°.运动中粒子仅受电场力作用.求: (1) 求电场强度的大小; (2) 为使粒子穿过电场后的动能增量最大,该粒子进入电场时的速度应为多大? 注:由于本题第(3)问不涉及动态问题,所以暂不展示. (1) 由题意知粒子在A点速度为0,它将会沿着电场线方向运动,因为q>0,故电场线的方向由A指向C,由题中条件分析可知 xAC=R. 由动能定理 解得 图6 动态图解法粒子运动轨迹示意图 (2) 由题意可知,粒子动能增量最大,则它必然沿电场线方向移动距离最多,粒子的初速度与电场线垂直,则它将做类平抛运动,以抛出点为原点,初速度的方向为x轴正方向,电场线方向为y轴正方向建立如图所示坐标系,任找一条运动轨迹(初速度较大),与圆周交于一点E,通过E做x、y轴的平行线,与y轴的交点为F,则AF即为沿着电场力方向发生的位移,逐渐减小初速度,则F点将下移,同时AF也将增大,当EF刚好与圆周相切时,沿电场力方向发生的位移是最大的,继续减小初速度,此位移将开始将小,所以E1F1与圆相切时射出时沿电场线方向移动距离最多,在此图中,切点即为E1点, 根据类平抛运动,结合几何关系有 x=Rsin60°=v1t, 根据牛顿第二定律有qE=ma. 联立解得粒子刚进入电场时的速度 动态图解决高中物理问题可应用于很多情境中,例如在高中物理经典的“小船过河”题目中,就可以应用“动态图”解法进行解决.让我们来看下面这个题目. 已知一条小河的水流速度为v水,小河的宽度为L,船在静水中的航行速度为v2,当v2小于v1时,小船应该如何行驶,才能使得小船的航行路程最短? 图7 “小船过河”各物理量示意图 若v船 无论是力学部分的题目,还是电学部分的题目,解决动态物理问题的思路都应该是紧密加深对理论知识的理解,教材中的知识和定义是考生解决高中物理动态问题的有效途径.从上述题目中可以看出运用几何图形进行表述、分析物理问题是高考考查的一个既定方向.[1]例如上述2020年全国Ⅰ卷中的第18题,整体思路就是运用动态图的解题方法,找出相关临界状态,从而使问题得到解决.在高考复习中,我们必须加强对教材中相关重要图像的教学,加强学生数形结合意识的培养,全面提升学生作图、识图的能力,从而培养学生的发散思维、树立良好的数理思想、建立物理模型,促进学生对问题情境有更加深入的理解,对物理过程有更加透彻的分析,达到培养学生高阶思维的能力和发展学生核心素养的目标.[2-4]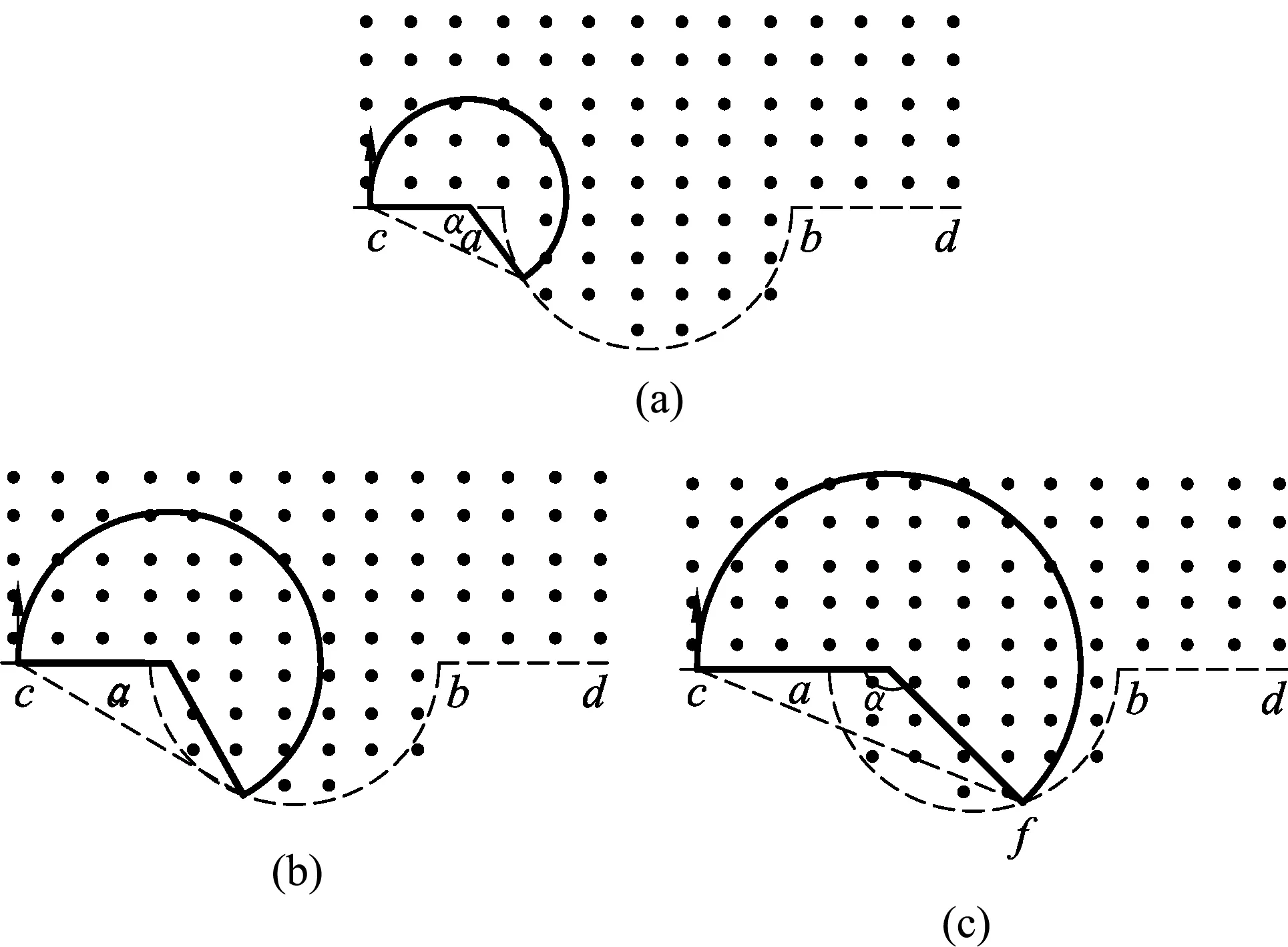
3 原题呈现

4 动态图解法探析
5 题型拓展
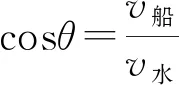

6 结语
